压力容器气体泄漏中的FSWT 和SVM 联合检测方法*

李 鹏陆 一杨佳康徐永凯

(1.南京信息工程大学,江苏省气象探测与信息处理重点实验室,江苏 南京 210044；2.南京信息工程大学,江苏省大气环境与装备技术协同创新中心,江苏 南京 210044；3.无锡学院自动化学院,江苏 无锡 214105)

危化气体是工业生产、存储和运转必不可少的组成部分,一旦发生危化气体泄漏,将对生命、财产、环境产生重大影响[1],如何对气体泄漏进行检测,及时发现并消除泄漏故障是减少此类事故发生的途径之一。因此,研究人员提出各种检测气体泄漏技术,如D-S 证据理论微小孔检测[2]、红外图像检测[3]和声学检测方法[4],其中声学检测方法具有较高的灵敏度、效率和精度。

在声学检测方法中,气体逸出压力容器的声音信号通常是非平稳的,采用时频分析方法能够有效分析非平稳信号。Yan 等[5]提出一种新的时频分析方法-频率切片小波变换(Frequency Slice Wavelet Transform,FSWT),从频域的角度引入了频率切片函数(Frequency Slice Function,FSF),实现时频分析功能。近年来,该分析方法被应用到轴承故障诊断[6]、大地电磁信号去噪[7]、生物信号分析[8]等领域,引入该方法对泄漏声信号进行时频分析,并依据该方法提取相应的特征做后续处理。此外,在实际应用过程中,仅判断出有无气体泄漏往往不能给工程维修人员提供有效的故障维修信息,因此有必要提出气体泄漏程度的判断方法。随着人工智能的发展,研究人员已经使用机器学习的方法来检测泄漏并对其进行分类。其中,支持向量机(Support Vector Machine,SVM)作为分类问题的监督学习方法被广泛使用。Mandal 等[9]提出了基于粗糙集理论和SVM 的泄漏检测方案,实验结果表明精度达到95.19%。El-Zahab 等[10]提出一种用于泄漏检测的线性SVM 模型,其准确率为96.44%。在实际应用中,用于建立SVM 分类器的特征或者指标受到噪声影响、压力容器内部压力变化等影响较大,鲁棒性不强,鉴于声学信号的非平稳特性,将时域、频域和时频域特征相结合更加合理。

针对上述不足,将FSWT 与SVM 相结合,提出了一种判断气体容器是否存在泄漏和泄漏程度识别的综合方法。首先,使用FSWT 对容器泄漏声信号进行去噪,研究泄漏声信号的优化基础和特征。其次,基于变换结果,提出了一种高质量的时频特征来识别不同泄漏程度,采用一种特征选择方法来减少冗余特征,提高预测性能,减少训练和利用时间。然后利用所选择的特征建立SVM 分类器,以网格搜索的方式搜索适合的SVM 值,使检测准确率达到最大。最后通过实验验证该方法的有效性。

1 基本理论

1.1 频率切片小波变换

假设信号f(t)∈L2(R),为f(t)的傅里叶变换,为频率切片函数p(t)的傅里叶变换,则从频域上定义的FSWT 为[5]:

式中:t为观测时间；w为观测频率；λ为能量系数,通常取1；u为评估频率；σ为尺度因子或w、t、u的函数；*表示共轭；i 为虚数单位。

根据Parseval 能量守恒关系和傅里叶变换对偶关系列出:

求得其时域表达式为:

为了便于分析,引入新的尺度参数κ=w/σ,则频率分辨率η可以表示为[11]:

式中:Δw=σΔwp为频窗宽度；Δwp为频率切片函数的窗宽；w为中心频率。此时公式可表示为:

频率切片函数有多种构造方式,可以把它看作是时频域上的带通滤波器[11],其构造方式需满足以下4 个条件:

FSF 通常具有波动性、衰减性等特征[12],根据其性质列出如下6 种函数以供选择:

式(10)为高斯函数,由于Heisenberg 不等式只在高斯函数处取等号,高斯函数也是短时傅里叶变换(Short-Time Fourier Transform,STFT)最优时间局部化的窗函数,因此式(10)相比其他的FSF 具有较好的时频分辨率,FSWT 本质上可以理解为STFT 的延伸发展。

FSWT 在进行逆变换时,可对任意时频区间(t1,t2,w1,w2)内的需求信号分量进行重构,重构后的信号fx(t)为[13]:

1.2 支持向量机

SVM 是由Vapnic 和Cortes 引入的有监督的机器学习方法,目前被广泛应用于分类和回归中[14]。SVM 是一个二分类算法,图1 所示,通过在正和负之间寻找一个超平面将它们区分开。假设给定一组带有标签yi=±1 的训练集数据x1,x2,…,xn∈ℝd,SVM 寻找一个最合适的超平面使支持向量之间有最大的函数间隔,这个超平面被定义为:

图1 SVM 数据分类

式中:w 是权重向量；x 是提取的信号特征,b是偏差。

SVM 通过解决以下最优化问题进行二分类:

式中:n是样本个数,‖ ‖是范数矩阵。考虑到实际存在异常离群点,引入松弛变量ξ解决因离群点导致不满足分类条件的问题,则SVM 数学模型可优化为:

式中:C是离群点权重,C越大表示离群点对目标函数影响越大,ξi是松弛变量。根据统计学方法和最优化理论,最终的最优解问题为:

式中:λi,yi是拉格朗日乘子[15]。

2 检测方法

所提出的基于FSWT 和SVM 的气体泄漏诊断主要包括3 个部分:①数据预处理,②特征提取,③泄漏分类,图2 为泄漏检测方法流程。

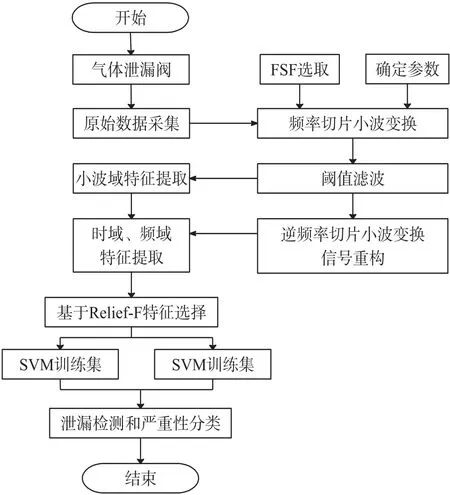
图2 检测流程

2.1 数据预处理

采集信号必然会存在干扰信号,进一步分析前要进行滤波处理,采用FSWT 方法对信号从时频域进行滤波处理,其步骤如下:

(1)采用FSWT 对气体泄漏信号进行分解,得到在全频带下的时频分布；

(2)采用时频域阈值滤波的方式对信号进行处理:

式中:κ为尺度参数,tn=,σ为噪声的标准差；N是信号长度[16]；

(3)对滤波后的时频域选择性进行逆变换重构,分离出有效气体泄漏声信号进行分析；

(4)进一步对去噪后的信号进行特征提取。

2.2 特征提取和选择

特征提取的目的是从数据集中确定、量化和描述与待研究问题相关的对象特征。将不同严重程度的去噪信号分割成一系列长度相同的子信号,从中提取时域、频域和时频域特征来检测是否存在泄漏以及泄漏的程度。传统时域特征包含最大值、最小值、峰峰值、绝对平均值、方差、标准差、峭度、均方根、波形因子、峰值因子、峭度因子、裕度因子,频域特征包括中心频率、总谐波失真。利用FSWT 将信号扩展到时频域分析,经过分析观察可以发现气体泄漏产生的声信号具有宽频带、分散性等特点,在超声范围内的30 kHz 和50 kHz 内拥有高于可听声范围的能量,其能量集中程度随着泄漏孔径的变化而变化,因此可以用平均频率表示能量集中程度的特征,可以表示为:

式中:W(t,f)是信号的FSWT 后每一个时频点的值,f是信号频率。提取30 kHz～50 kHz 之间的信号分成128 个时间间隔ti(i=1,2,…,128),选取均匀泄漏的时间段,求Ωf(ti)分别在观测范围为30k～40k、40k～50k、30k～50k 的平均值,获取均匀泄漏时不同频带信号的能量集中程度用于后续的分析。

为了提高SVM 分类能力、减小运算量,采用Relief-F 算法[17],根据不同的特征区分它们对应特征向量的能力进行权重估计。根据各个不同类别特征数据之间的相关性,其计算公式如下:

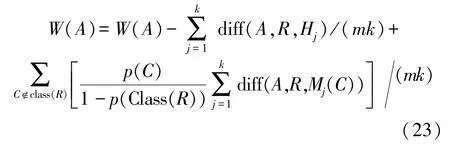
式中:diff(A,R1,R2)表示样本R1和样本R2在特征A上的差值,体现各样本之间的特征距离的大小,可表示为:

式中:Ri表示从随机信号中选取的一个特征向量；A表示某一特征；Hj表示和Ri同类样本集中的k个邻近样本(nearest Hits)；Mj表示和Ri不同类别样本集中的k个邻近样本(nearest Misses)；P(C)表示C类样本占样本总数比例；m表示抽样次数。根据Relief-F 算法结果,将具有较大权重值的特征作为SVM 输入。

2.3 分类方法

在众多的分类器中,SVM 能够处理异常值求得全局最优解,具备选取非线性边界能力[18]。然而大多数情况下的特征空间是高维的,需要大量的计算工作,因此使用核函数(Kernal Function)能够将特征映射计算转换成特征空间的点积运算:

所以式(20)变成:

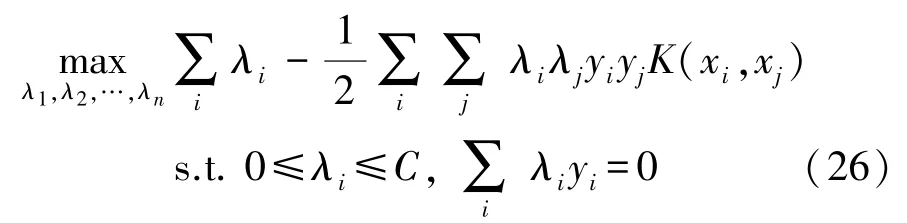
通过以下决策规则可对x进行分类:

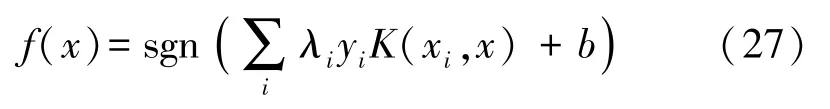
采用一对一法(one-versus-one)进行多分类,其核心思想是在任意两类样本之间插入SVM,因此对n类样本需要设计n(n-1)/2 个SVM,对测试集数据分别进行二分类并投票计数,将得票数多的类别归为该测试数的类别。本文将气体泄漏归为4 个严重程度:无泄漏、轻微泄漏、中度泄漏和严重泄漏,通过模拟泄漏环境进行实验论证。

3 实验测试

3.1 实验搭建

所设计的气体泄漏数据采集系统如图3 所示。

图3 数据采集方案

在这套实验方案图中,1 是产生气体的氮气瓶；2 是氮气瓶的出气部分为带有压强刻度的减压阀；3 是有着不同尺寸孔径的小帽,用于模拟不同严重程度的气体泄漏故障；4 是宽频带的麦克风传感器,其性能指标如表1 所示；5 是Analog Discovery 2-NI Edition 采集卡；6 是waveforms 软件,用于记录采集数据。

表1 麦克风参数

3.2 信号采集与分析

考虑到气体泄漏声信号能量主要集中在超声范围,因此选取宽频带麦克分探头观测超声信号,将采集卡采样频率设置为200 kHz 保证采样信号质量。结合实际,将0.5 mm、1.5 mm、3.0mm 泄漏孔径定义为轻微泄漏、中度泄漏、严重泄漏,图4 是对3 种不同泄漏孔径下的声信号从时域、频域的分析,可以发现不论何种孔径,泄漏声信号能量都集中在超声部分；随着泄漏孔径的增大,频谱开始出现能量分散的趋势,并且在超声部分逐步地向50 kHz 集中。因此从超声范围内对声信号特征进行分析和提取是很有必要的。

图4 不同孔径泄漏信号频谱图

选取适当的尺度因子取值能够获取较好的时域分辨率和频域分辨率,减少图像端点处的边界效应,根据文献[5],选取Δw·Δt=0.5,η=0.05,κ=23.54以获取较好的分辨率,图7 分别为不同孔径泄漏声信号进行FSWT 变换和降噪后的结果,其中图7 的第1 列a 和b 为0.5 mm 孔径气体泄漏声信号时频图、c 为降噪后的时频图、d 为选取观测频率为30 kHz～50 kHz 进行重构后的时域图,同理第2 列、第3 列分别是1.5 mm 和3.0 mm 泄漏孔径声信号对应的降噪前后的时频图和重构后的时域图。从图7中可以发现,在泄漏伊始最先产生超声信号且超声部分信号幅值较大,将重构后的时域信号和原始信号进行比对,发现滤波后的信号更为平滑,减少了毛刺。按照前文的特征提取方法,对信号各类特征进行Relief-F 权重分析,其结果如表2所示。

表2 各特征权重值

图5 是采集信号的三维散点图,每一个点代表一次泄漏信息,将选取的3 个典型特征作为坐标轴,录入三维视图中可以清晰的看出,这3 个特征有明显的聚类行为,说明分析筛选后的特征具有较强的鲁棒性,可以作为鉴别泄漏程度的泄漏特征使用。

图5 前三个权重特征的散点图

3.3 泄漏分类

选取判别能力最强的前6 个特征作为SVM 的特征输入,将70%的数据用于训练集,剩余的数据用于测试集,选取高斯核函数作为核函数,采用十字交叉验证对分类性能进行估计。由于此方法需要对惩罚系数c和高斯核函数自带参数g进行确定,为了最大限度地提高验证精度,使用网络搜索的方法对参数进行优化处理,将c、g变化范围设置为-10～10 进行遍历搜索[19]。

先建立二分类SVM 进行识别泄漏状态和非泄漏状态,当c=0.435 3,g=0.164 9 时的SVM 对泄漏状态和无泄漏状态判断准确率达到99.75%,表明该方法具有较强的泄漏有无的判准能力。然后对泄漏状态的严重程度进行分类,图6 表明了按照权重排列的不同输入特征数量和分类结果的关系,按照排序依次选取不同数量的特征送入SVM,结果表明输入特征数随着数量增加而增加,当特征数为6 时,准确率达到了最高94.68%,此时c=1.319 5,g=0.435 3,当特征数继续增加时,准确率略微下降,结果与输入6 个特征时相近,表明经过Relief-F 算法筛选出的特征能够较好地代表气体泄漏声信号。

图6 SVM 输入特征数量和准确率关系

图7 不同孔径气体泄漏声信号分析

由此可知,在这项研究中提出的方法能够保证泄漏检测的精确度和泄漏程度识别的准确性,这就意味着选择的FSWT 算法分析信号、阈值滤波能够对原始信号进行有效的降噪,提出对重构后的信号从时频域不同的频段、时间段求取平均频率能够有效地代表气体泄漏声音信号的明显特征。

采用基于声信号特征分析方法有助于提高SVM的预测性能。表3 给出了部分研究者的方法、特征选取和研究结果以及采用决策树、BP 神经网络作为参照组的算法比对,可以看出所采用的基于FSWT 的去噪方法、提出平均频率特征、基于Relief-F 的特征筛选能够有效地提高SVM 的分类准确度。

表3 部分方法、所选特征和准确度的比较

4 结语

本文提出了一种基于FSWT 和SVM 的气体泄漏检测方法,从声音的角度去分析和判断气体泄漏。FSWT 能够精确地呈现气体泄漏声信号的时频能量分布特征,可用于研究气体泄漏的时频特征。对声音信号进行阈值滤波和逆变换重构,有效地去除了噪声信号的干扰。在此基础上,通过时域、频域和时频域提取去噪后的声信号特征,并进行权重排序,选取权重值较大的6 个特征输入到SVM 进行分类,对泄漏与否判断准确率达到99.75%,对无泄漏、泄漏孔径为0.5 mm 的轻微泄漏、1.5 mm 的中度泄漏、3 mm 的严重泄漏分类识别准确率达到94.68%。结果表明该方法有良好的检测泄漏的性能,不仅可以判断是否存在泄漏事故,同时可以诊断出泄漏程度,因此本文提出的气体泄漏诊断方案具有应用价值,有助于检测泄漏和泄漏孔定位研究。