一种高线性度低失真跨导运算放大器的设计*

蒋思中，覃志松

(1.广西职业技术学院智能制造学院,广西 南宁 530226；2.桂林电子科技大学计算机与信息安全学院,广西 桂林 541004)

许多模拟集成电路如波形发生器、可变增益放大器、连续时间滤波器等[1-3],均使用OTA 作为其基本构件。其性能取决于OTA 的各种参数,例如线性,谐波失真,电流消耗,噪声以及跨导在输入电压范围内的变化等。通常要求OTA 在宽输入电压范围内具有良好的线性度,同时具有低谐波失真和低噪声。在差分OTA 中,偶数阶谐波由于其差分特性而变得无关紧要。但差分输出中奇数阶谐波分量会降低OTA 的线性度性能[4-5]。

为了提高OTA 的线性度,必须最小化差分对输出的奇数次谐波分量,从而降低由这些谐波引起的失真。为此,许多研究人员进行了各种尝试,例如采用源极退化[6]、伪差分对[7]、交叉耦合差分对[8]和电流分配[9]等技术。Soares C F T 等[10]和Hwang B W等[11]则尝试将上述技术进行结合从而减小失真,均获得了适合低频应用的线性度改善。但这些方法只是实现了有限的线性范围,且失真性能仍不够理想。

如前所述,OTA 在连续时间型滤波器的设计中起着重要的作用。在要求低噪声、低失调、电源电压较低的现代应用中,连续时间有源滤波器比开关电容滤波器更受关注。尽管开关电容(switched capacitor,SC)滤波器具有高精度和高可调谐性[12-13],但很难适用于低频应用。有源电阻-电容(Resistor-Capacitance,RC)滤波器使用运算放大器、电阻和电容。电阻和电容的尺寸使它们无法应用于频率很低的集成电路。因此,跨导放大器-电容(OTA-Capacitor,OTA-C)连续时间型滤波器[14]已成为现代低频应用的最佳选择之一,其中OTA 是设计这些滤波器的基本构件。这些滤波器的截止频率是利用OTA单元的跨导和电容值来确定的。

因此,为了通过减小谐波失真来改善线性度,提出了一种基于源极退化和辅助差分对技术的全差分高线性度OTA。此外,采用该OTA 设计并仿真了二阶连续时间型全差分低通滤波器。实验结果验证了所提方法的可行性。

1 差分对理论分析

OTA 本质上是一种压控电流源,其中输入电压通过差分对转换为差分输出电流。 各种类型差分对的原理[15-17]如图1 所示。

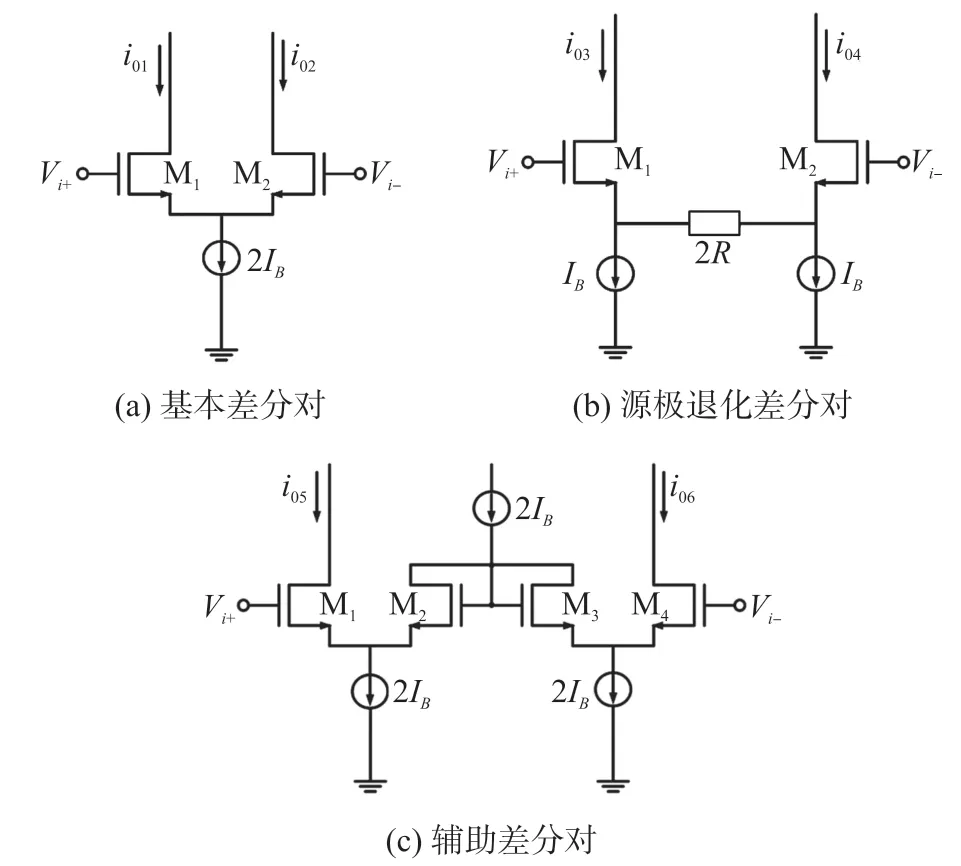
图1 各种类型差分对的原理

图1(a)中M1和M2的漏极电流i01和i02可以表示为:

式中:Vid=(Vi＋-Vi-)表示差分输入电压。βn表示输入晶体管的跨导参数,Gm表示差分对的跨导。 通过使用泰勒级数展开上述表达式为:

从式(3)和式(4)可以看出:差分对的输出电流中存在三次和更高阶的奇次谐波。 三次谐波分量对输出电流的失真影响最大,该三次谐波失真系数(HD3)可以表示为:

式中:VGS表示最大栅源电压,Vth表示驱动门限。

源极退化是一种降低差分对的HD3和Gm的技术。 输出端失真分量的减少增加了线性范围,从而在宽输入电压范围内保持恒定的Gm值。 在这种技术中,可以在输入晶体管的源极连接1 个电阻,如图1(b)所示。 假设电阻值为2R,输入差分对的漏极电流及其合成跨导和三次谐波失真系数(HD′3)可表示为:

对于辅助差分对配置来说,差分电压可以被分成多个差分对[18]。 在此配置中,输入电压在辅助对之间共享,如图1(c)所示。 M1、M2和M3、M4形成2个具有相同长宽比的差分对。 假设n是差分对的数目,OTA 的跨导和三次谐波失真分别减少n和n2。

2 提出的OTA

在本研究中,利用前面讨论的技术和沟道金属氧化物半导体管(P-channel Metal Oxide Semiconductor,PMOS)输入差分对,提出了一种采用源极退化和辅助差分对架构的全差分OTA,如图2 所示。

图2 提出的全差分OTA

在该结构中,2 对MOSFET(M1/M2、M3/M4)和值为2R的2 个电阻构成了差分对结构。这些电阻也可以用工作在线性区域的MOSFET 来替代,如图2 所示。设这些源极退化电阻提供的电阻各为“2R”。在该技术中,差分输入电压在2 个差分对之间平均分配,并且源极退化。PMOS 差分对的跨导为Gmp,有效跨导(Gm,total)和三次谐波失真(HD3,total)将分别降低[n(1＋GmpR)]和[n(1＋GmpR)]2。图2中所提OTA 的电流、跨导和谐波失真的表达式为:

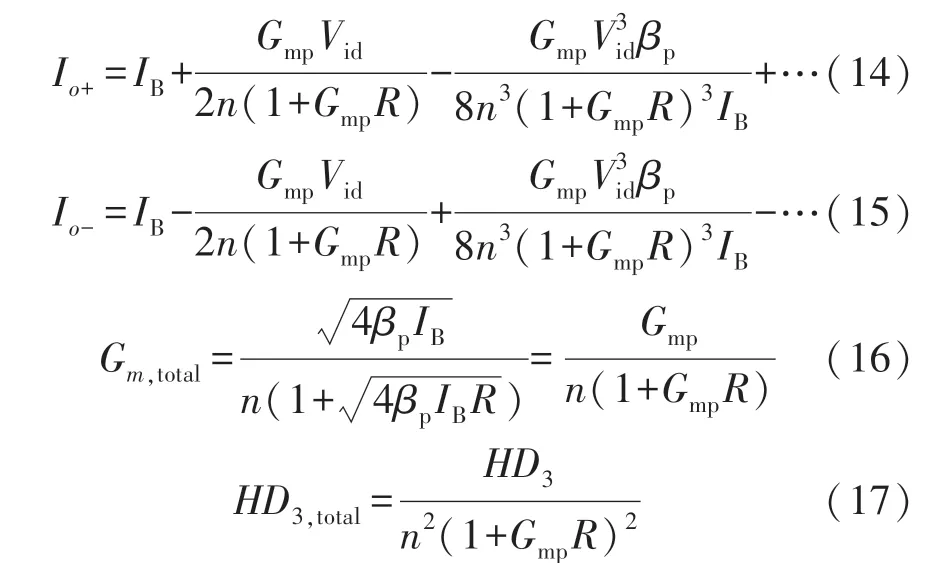
式中:βp表示PMOS 管的跨导参数,Gmp=,n=2。

通过上面的表达式可以很容易看出,谐波失真得到了减小,从而线性度得到了同等程度的改善,所提OTA 单元的总跨导得到降低,从而可有效地应用于OTA-C 滤波器(低频应用)设计。

3 提出的滤波器

采用低失真、高线性度的全差分OTA 设计了一个二阶低通滤波器,如图3 所示。该滤波器使用4个OTA 和2 个不同的电容值。

图3 采用所提OTA 的二阶低通滤波器

由于所提OTA 具有低跨导值和高线性度的优点,因此该滤波器可以工作在低频。滤波器的传递函数导出为:

式中:gm1、gm2、gm3和gm4分别表示图3 中4 个OTA(从左至右)的跨导,c1和c2分别表示两个不同的电容值。

为了获得单位增益滤波器响应,使用了相同的OTA。在此假设下,传递函数简化为:

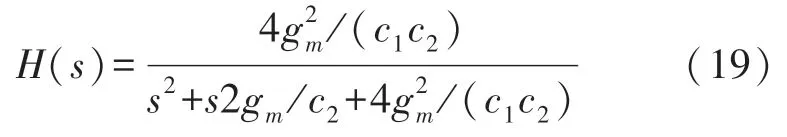
通过将式(19)与低通滤波器的一般传递函数进行比较,可将截止频率ωn和品质因数Q分别表示为:

4 仿真结果与分析

本节采用SCL 180 nm CMOS 工艺,在1.8 V 电源电压下对所提OTA 和滤波器进行了设计和仿真。所有OTA 的偏置电流都设置为10 μA。不同输入电压下所提OTA 的输出电流和跨导变化,如图4 所示。

在图4 中可以清楚地看到,与其他架构的差分对相比,所提OTA 的线性范围显著增加。所提OTA的Gm降低了[n(1＋GmpR)]倍,获得的跨导约为6.12 μS。

图4 所提OTA 的输出电流和跨导变化

在1%跨导变化的情况下,所提OTA 获得了大约0.9 V 的线性范围。分别改变峰间输入电压和输入信号频率,绘出了三次谐波失真分量(HD3)和互调失真分量(IM3)变化情况,如图5 和图6 所示。

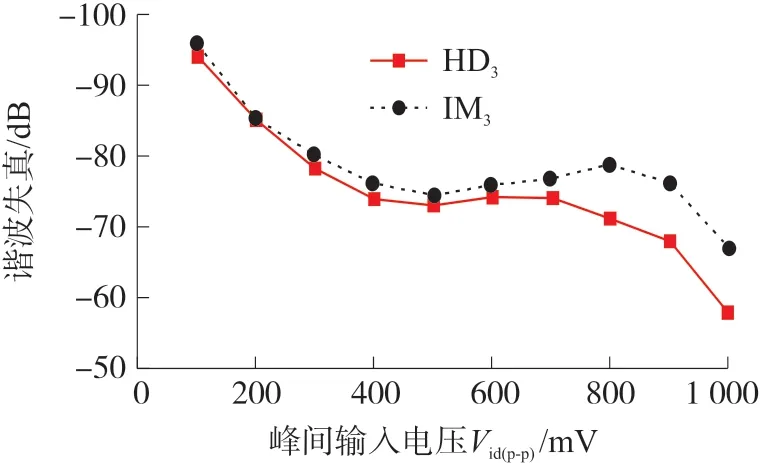
图5 峰间输入电压变化时的谐波失真(1 MHz 输入信号频率)

图6 输入信号频率变化时的谐波失真(500 mV 峰间输入电压)

当峰间输入电压Vid(P-P)为600 mV、差分输入为1 MHz 时,所提OTA 的HD3和IM3分别为-74.3 dB和-75.5 dB,功耗约为64 μW。在1 MHz 信号频率下,OTA 的共模抑制比(common mode rejection ratio,CMRR)约为80 dB。

利用提出的OTA,设计并仿真了单位增益二阶全差分低通滤波器。该滤波器通过改变电容值来设计不同的截止频率。品质因子设置为0.5。通过将C2值设置为5 pF,滤波器的截止频率约为96 kHz。对于不同的C2值,滤波器的频率响应如图7 所示。

图7 不同电容值下二阶滤波器的频率响应

通过将C2从0.5 pF 至10 pF 变化来获得100 kHz～300 kHz 的截止频率。滤波器输出端的有限增益效应导致低频增益下降约15%。输入信号频率为10 kHz 条件下,峰间输入电压变化时的滤波器谐波失真分量如图8 所示。

图8 峰间输入电压变化时的滤波器谐波失真(10 kHz 输入信号频率)

从图8 可以看出,该滤波器的性能在较宽的差分输入电压范围内保持不变。

为了检验失配对滤波器性能的影响,在随机分布条件下(样本数为100)进行了蒙特卡洛仿真。为了执行蒙特卡罗分析,将C2值设置为5 pF。滤波器中每个OTA 单元的输入晶体管有5%的失配,差分输入的信号频率10 kHz,峰间输入电压为300 mV时,所设计滤波器的HD3和带宽如图9 所示。

图9 蒙特卡罗仿真结果(样本数为100)

从图9 所示的蒙特卡罗结果可以看出,滤波器的HD3和带宽与它们的平均值仅相差2%,从而保证了设计的稳健性。所设计的滤波器功耗约为258 μW。电容(C2)值为5 pF 的滤波器版图如图10所示。该过滤器的面积为0.145 2 mm2,截止频率的变化小于1%。

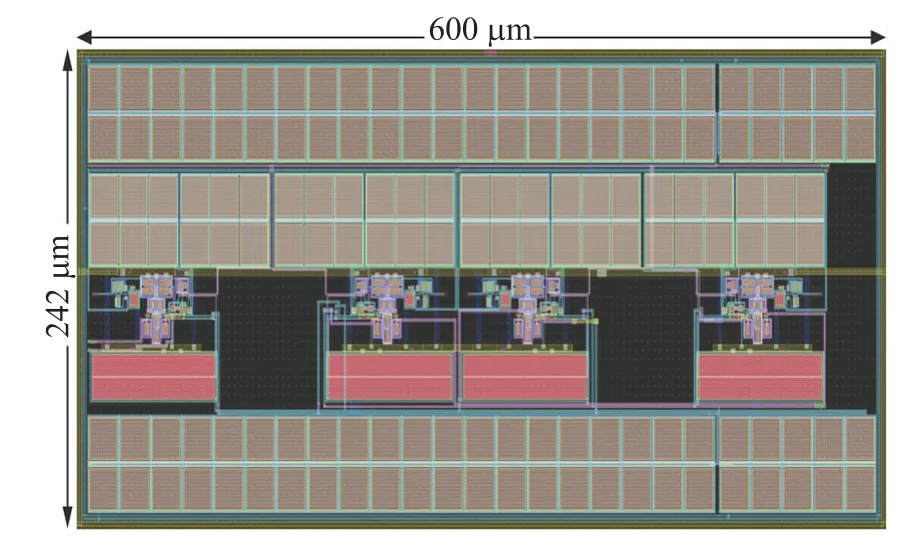
图10 滤波器版图

所提出OTA 和滤波器的性能总结如表1 所示。

表1 提出的OTA 和滤波器的性能总结

将所提OTA 和滤波器的性能与已提出的设计[6,10-11]进行了对比,如表2 所示。

表2 提出OTA 和滤波器的性能对比

从表2 可以看出,提出的OTA 可以提供较小的跨导,这使得它适合于低频滤波器的应用。对于1%的跨导变化,与Kar 等[6]中的500 mV 相比,所提出设计实现了明显更高的900 mV 线性范围。OTA的失真性能优于表2 中的所有其他设计,且与Kar等[6]和Soares 等[10]相比,功耗更低。Hwang 等[11]的OTA 比所提设计消耗更少的功率,因为它是在较低电源电压、0.13 μm 工艺技术中实现的。总体来说,与所有其他设计相比,所提出OTA 和滤波器实现了更好的线性度和失真性能,且功耗较低。

5 结论

提出了一种高度线性、低失真的运算跨导放大器。该OTA 采用SCL 180 nm CMOS 工艺设计,电源电压为1.8 V。在跨导变化约为1%的情况下,实现了900 mV 的宽线性度范围。此外,利用该OTA 设计了一个二阶连续时间型全差分低通滤波器。实验结果表明,该OTA 和滤波器具有优秀的线性度和失真性能。除连续时间滤波器之外,该OTA 还可以用于其他低频电流模式电路。