基于功率预测变步长扰动观察法的最大功率追踪
2021-10-26付光杰江雨泽吕春明周禹彤
付光杰, 暴 蕊, 江雨泽, 吕春明, 周禹彤
(1. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318; 2. 哈尔滨科学技术职业学院 现代服务学院, 哈尔滨 150300)
0 引 言
目前全球能源危机日益严重, 由于太阳能是一种理想的清洁能源, 因此受到了世界各国的重视, 而光伏发电产业已经在世界各国能源结构中占据着举足轻重的地位[1-3]。但光伏电池的利用率低、 成本高依然是阻碍其应用的难题, 所以最大功率点追踪(MPPT: Maximum Power Point Tracking)技术是当前研究的重点。针对MPPT技术, 国内外学者提出的方法中扰动观察法(P&O: Perturbation & Observation method)因其结构简单且实效性好而被广泛应用。但其也有无法兼顾追踪速度和精度的缺点, 为此出现了很多改进的P&O法。
闫瑞杰等[4]将P&O与牛顿差值法相结合提出一种复合的控制策略, 根据牛顿差值法得到的近似曲线追踪到最大功率, 但只提高了追踪速度; 梁国壮等[5]将扰动观察和模糊控制结合成一种复合法, 将寻优速度提高了0.35 s; Ahmed等[6]提出最大功率简化稳态点的跟踪方法, 缓解了传统P&O的振荡趋势; 张国梁等[7]通过改变功率对电压的比值改善了输出性能; 陈令军等[8]提出一种新的变步长算法, 虽然提高了速度, 但精度问题还没有很好地解决。为此笔者提出了一种基于功率预测的变步长P&O法, 利用步长较大的传统扰动观察法的快速性追踪到最大功率点附近, 然后进行线性化功率预测, 进而精确地追踪到最大功率点。
1 光伏电池建模及其输出特性
1.1 光伏电池建模
光伏电池是光伏系统的重要组成部分, 发电原理是半导体光生伏打效应[9]。太阳光激发半导体后, 电子和空穴因为分别带负电荷和正电荷而移动到不同区域, 在PN结两端大量累积而形成电动势。光伏电池等效电路如图1所示, 其数学模型如下
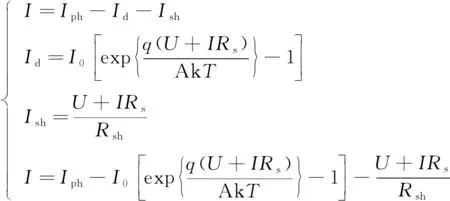
(1)

图1 光伏电池等效电路图Fig.1 Equivalent circuit diagram of photovoltaic cell
其中Iph为光电流;Id为二极管反向饱和电流;Rs为内部等效串联电阻;Rsh为内部等效旁路电阻;A为二极管因子;k=1.38×10-23J/K为卡尔曼常数;T为光伏电池表面温度。
由于数学模型(1)能较大程度还原光伏电池单元的基本原理, 所以被广泛应用于太阳电池的理论分析中, 但由于式(1)中的Iph、I0、Rs、A和Rsh受温度和光强的影响, 因而很难确定参数值, 因此不便于工程应用, 所以笔者采用文献[10]中的数学模型, 即

(2)
其中Isc、Im、Uoc、Um分别为任意光强与温度下对应的短路电流、 MPP(Maximum Power Point )处电流、 开路电压以及MPP处电压。这4个参数只需太阳能电池供应商提供, 且有
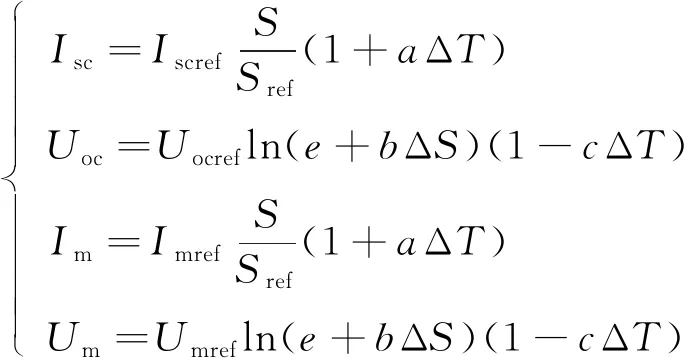
(3)
其中ΔT为温度变化量; ΔS为光强变化量;a、b、c经大量实验总结的典型值分别为0.002 5 ℃、0.000 5 W/m2、0.002 88 ℃。对于不同的温度和光强, 由式(3)可得Isc、Uoc、Im和Um的大小。
2.2 光伏模块输出特性曲线
在Matlab R2017b中搭建PV模块, 其中PV模块的各项参数如表1所示。
当光强固定为1 000 W/m2, 设温度T分别为25 ℃、35 ℃和45 ℃得到光伏模块的I-U、P-U曲线如图2所示; 当温度固定为25 ℃, 设光强S分别为1 000 W/m2、 800 W/m2和600 W/m2得到光伏模块的I-U、P-U曲线如图3所示。
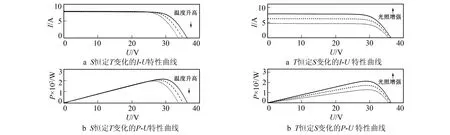
图2 S恒定T变化的特性曲线 图3 T恒定S变化的特性曲线 Fig.2 Characteristic curve of S Fig.3 Characteristic curve of constant and T changing constant T and change of S
3 传统的扰动观察法及其改进
3.1 传统扰动观察法
P&O法是基本的MPPT控制算法, 其流程如图4所示。
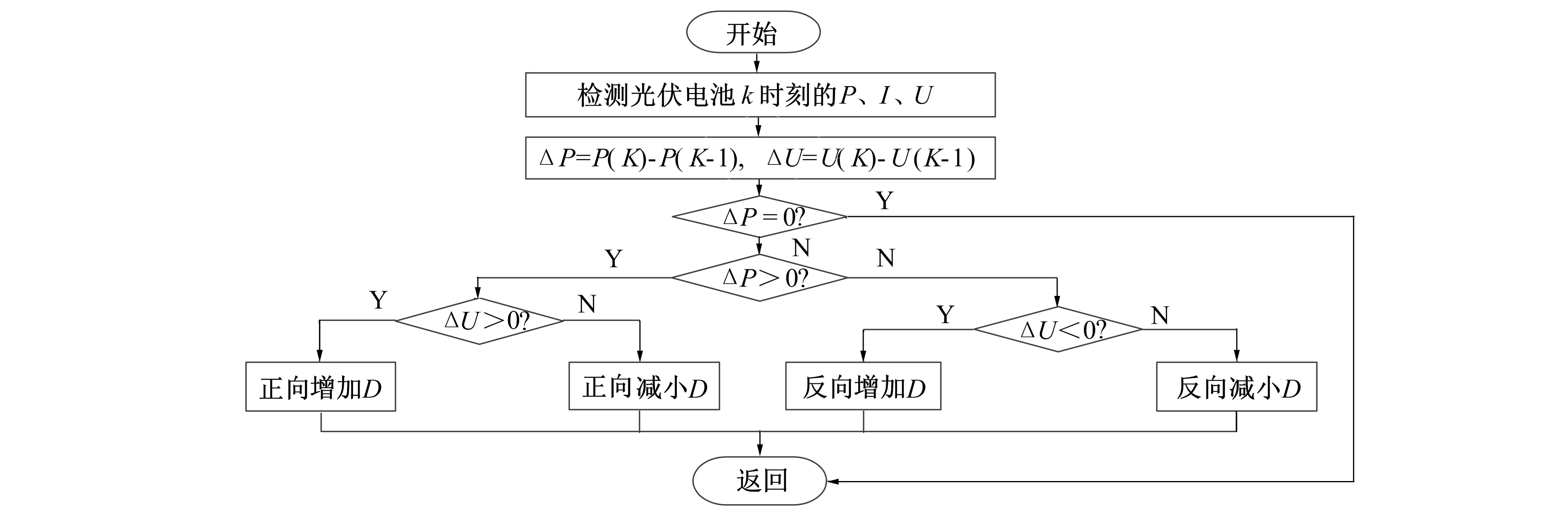
图4 传统扰动观察法流程图Fig.4 Flow chart of traditional perturbation observation method
P&O法就是实时改变整个系统的工作状态, 通过判断增加电压扰动后输出功率的大小, 跟踪光伏电池的最大功率点, 进而实现光伏电池的最大功率输出。其采用了一种主动搜寻最优点的方式, 动态性能很好, 但稳定性较差。由于传统的P&O算法有如下3个缺点: 振荡、 误判以及追踪速度慢, 从而限制了其使用[11-16]。
2.2 改进的扰动观察法
首先, 从扰动观察法的动态跟踪过程可以看出, 始终存在一个干扰电压ΔU, 即使外部环境没有变化, 振荡仍会发生在最大输出值附近。如图5所示, 某一时刻, 当光伏组件在A点工作时其输出功率为PA, 此时运行点电压受到干扰ΔU, 运行状态更新到B点。变化值ΔU>0、ΔP>0, 根据传统的扰动观察法原理, 扰动方向正确, 将继续正向增加扰动电压ΔU更新到C点。此时变化值ΔU>0, 但ΔP<0, 则系统将会反方向增加扰动电压ΔU回到B点。可见, 最大功率输出点在A、B、C 3个点反复跳动, 导致了输出值在最大值附近振荡。
其次当外部环境突然变化时, 传统的扰动观察法容易出现误判。如图6所示, 某一时刻, 光伏电池的输出功率为PA。若环境条件不变, 正向增加电压扰动ΔU, 在L点, 时间不变, 则输出功率变为PL, 变化值ΔU>0、 ΔP>0。如果光强在L点突然变化到B点的大小, 输出功率也相应变为PB, 此时干扰在最大功率点左侧。但若ΔP*<0时, 算法将会判断干扰位于最大功率点右侧, 导致判断错误, 影响输出的准确性。

图5 振荡现象分析图 图6 误判现象分析图 Fig.5 Analysis diagram of oscillation phenomenon Fig.6 Misjudgment phenomenon analysis diagram
此外, 传统的P&O法虽然结构简单容易实现, 但步长大小很难选择。当步长较大时, 搜索最大功率点的速度明显提高, 但同时输出功率在MPP附近以较大幅度反复振荡, 无法准确跟踪MPP; 当步长很小, 虽然寻找最大功率点的准确性提高, 但动态响应速度较慢, 从而导致电池在工作效率低的输出区工作时间较长。基于对传统算法各种问题的具体分析, 笔者提出一种基于功率预测的变步长P&O算法。首先在工作点距离MPP较远时选择较大的步长以提高算法的响应速度, 尽快跟踪到MPP附近。
通过功率与电压之比确定步长的大小为

(4)
其中dP为电压扰动后第k+1次与k次的功率值之差; dU为电压扰动后k+1次与第k次的电压值之差;λ通常为0.1~0.2。

图7 功率预测原理图Fig.7 Schematic diagram of power prediction


(5)
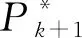
基于上述改进策略, 提出改进的扰动观察法流程如图8所示。
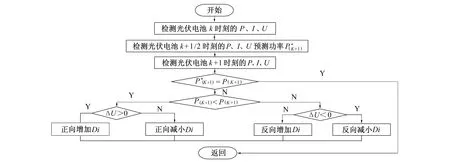
图8 变步长扰动观察法流程图Fig.8 Flow chart of perturbation observation method with variable step size
4 仿真分析
4.1 仿真原理图
对笔者提出改进的P&O法搭建的仿真模型如图9所示; 仿真参数如表2所示。

图9 变步长P&O算法仿真原理图Fig.9 Simulation schematic diagram of variable step size P&O algorithm

表2 仿真参数
因为直流系统中光伏电池端电压往往小于系统的输出电压, 所以仿真中的升压部分采用Boost升压斩波电路满足光伏系统的电压需求。最后通过MPPT、 PWM模块处理, 完成最大功率追踪。
4.2 仿真结果及分析
实验分别在0、0.2 s、0.4 s, 光强分别为1 000 W/m2、800 W/m2、 600 W/m2, 温度为25 ℃不变, 并在0.6 s内完成仿真。得到的改进前后P&O算法在MPPT中的应用对比如图10~图13所示。

图10 两种算法下的输出电流对比图Fig.10 Current changes under the two algorithms
由图10可以看出, 图10a中在追踪到最大功率点前, 振幅ΔI=5.68 A, 振荡时间持续到了0.148 s才接近MPP处, 在0.197 5 s达到了MPP处的最大输出电流, 但并不稳定, 在MPP附近有较大振荡; 而相同条件下, 改进的P&O法的仿真结果显示从0~0.045 s振荡明显, 振幅ΔI=1.84 A, 但0.187 9 s时就追踪到了最大输出电流, 相比于传统的P&O法追踪时间缩短了0.009 6 s, 振幅减小了3.84 A。此外, 在最大功率点附近的振荡情况也明显减缓。
利用传统的P&O法对输出电压进行追踪, 如图11a所示, 在0.179 5 s时输出最大电压17.7 V, 而且在0.2 s时振荡幅度依旧很明显, 当光强由1 000 W/m2降到800 W/m2时, 响应速度较慢; 而相同条件下改进的P&O如图11b所示, 当仿真时间为0.104 9 s时, 已经达到MPP处的输出电压, 且在受到光照以后的响应速度较快, 振荡也较小。
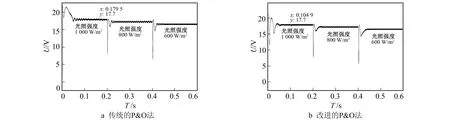
图11 两种算法下的输出电压对比图Fig.11 Voltage variation under the two algorithms
在输出功率的对比中, 由图12a可以看到, 在相同的光强和温度下, 传统的P&O的算法在0.047 s时才达到MPP附近, 且在追踪到MPP处输出功率之前, 有很大幅度的变化; 而由图12b可见, 改进的P&O在0.035 s就可以到达MPP处, 缩短了0.012 s。

图12 两种算法下的输出功率对比图Fig.12 Output power variation under the two algorithms
为更清楚地展现效果, 放大图12a,图12b中光强为1 000 W/m2的部分, 得到图13。仿真时间段均为0.185~0.2 s, 输出功率都是140.5 W。通过对比图中标记的波形可以看出, 传统的P&O法在0.2 s附近的振荡比改进的P&O算法明显得多。

图13 MPP处功率放大图Fig.13 Power enlargement at MPP
综上对输出电流、 电压和功率的对比, 有效地验证了改进的P&O法的在MPPT技术中的优越性和可行性。
5 结 语
笔者基于传统的P&O算法无法兼顾追踪速度和精度的缺点, 提出的基于功率预测的变步长P&O算法有效地改善了这一问题, 仿真结果表明改进的方法不仅降低了输出波形的振荡幅度, 而且保证了输出电压和输出电流的平衡, 改善了系统的输出性能, 达到了预期效果。
