基于双滤波器的高精度目标跟踪估计方法

秦健凯，李鹏

北京交通大学 电子信息工程学院，北京 100044

1 引言

航天器是当代获取空间信息的主要方式，如何获取太空中航天器的运动状态成为当前重点研究的问题之一。

空间目标在推进器作用下改变原轨迹进入新轨道，即轨道机动。空间目标轨道机动分为连续推力和脉冲机动两类，前一类可用于构造机动模型并同时估计模型参数与目标状态，后一类可通过机动检测策略来确定目标机动时刻，从而做出应对。对于存在脉冲机动的非合作目标，目前多采用天基平台进行观测，并设计相应的机动检测策略。天基平台的观测值具有非线性的特点，因此非线性滤波成为空间目标跟踪估计的主要方法之一[1]。

现有研究基于扩展卡尔曼滤波、双扩展卡尔曼滤波及改进的双重无迹卡尔曼滤波(DUKF)进行轨道或目标参数估计，获得了效果提升。但注意到简化摄动力的模型会导致累积误差，使用双扩展卡尔曼滤波对复杂非线性模型失效，或将状态和参数分别采用不同的观测方程估计，会导致解算复杂[2-4]。为此，本文考虑只用一个观测方程来精简描述，即选取加速度作为观测信息，方程既包含状态量又有参数量。在考虑太阳光压的基础上，基于DUKF进行估计，从而克服建模不准确及解算复杂的缺点，实现合作目标运动状态以及机动加速度的高效估计。

对非合作航天器，无法获得其加速度观测值以及机动信息。现有研究采用相对运动方程与滤波器切换策略实现目标跟踪，并对多种滤波算法的精度和收敛速度进行对比研究[5-7]。文献[8-9]以半长轴变化为变轨依据，通过联合策略实现机动下的半长轴检测，简化处理偏心率变化的情况。此外，对于地基观测，地面测控存在时延，且对于一些无法在全球布置测控站的地区还存在信号遮挡问题[10]。文献[11-12]综合考虑两个轨道根数，将偏心率作为辅助特征参数，设计目标状态噪声自适应调整策略。但要注意部分观测方法的限制较强，且复杂的模型方程会对滤波效率带来负面影响。为此，本文采用天基观测平台获得非合作目标的观测值，用半正焦弦代替半长轴，当检测到目标机动后进行滤波器切换，从而克服求解半长轴时可能无穷大的缺陷及对地基观测的依赖。进而，采用双EKF实现基于半正焦弦机动检测策略的非合作目标的高精度位置速度跟踪估计。

论文总体方案流程如图1所示。采用DUKF算法对存在连续推力的合作目标进行跟踪估计；采用双EKF结合机动检测策略对存在未知机动的非合作目标进行跟踪估计。为降低虚警，设定当连续检测到3个点满足要求时，认为目标发生机动。

图1 总体方案流程Fig.1 The flow chart of the overall scheme

2 理论基础

合作航天器可通过加速度计获取信息，而非合作航天器在信息获取方面不配合，可以将一个合作航天器作为天基观测平台来获取非合作目标的观测信息，建立相对运动方程，描述其运动状态。

2.1 航天器运动方程

(1)合作航天器运动方程

考虑可以产生连续推力的合作航天器，受到中心天体引力以及太阳光压摄动的影响，假设推力加速度方向与参考坐标系下三轴方向一致。目标的状态量X=[rvε]T，其中r为目标在参考系下的位置矢量，v为速度矢量，ε为反射因子。假设太阳光照有效面积不变，且考虑太阳光不能时刻垂直照射太阳翼，故用ε作为变量体现这一变化。目标的参数量θ=[m]其中m为航天器的质量。太阳光压摄动加速度为:

式中：AU为天文单位，1AU=1.496×108km；S为航天器受辐射有效面积；ρ=4.56×10-6N/m2为太阳辐射压强；CR=1+ε为太阳光反射系数；ε∈[0,1]。

机动加速度为：

式中：F=[FxFyFz]T为推力矢量；m0为航天器初始质量；Δt为机动持续时间。Isp为发动机比冲，gT为参考点引力加速度。合作航天器通过其携带的加速度计，可以获得除引力外的加速度大小，且初始质量、推进器类型等信息已知。

(2)非合作航天器运动方程

天基观测平台作为合作目标，可通过获得其运动状态建立天基平台下的轨道坐标系，通过相对运动方程描述非合作航天器的运动状态。天基平台通常基于微波雷达、光学相机等获得目标的相对距离及角度信息。对机动未知的非合作航天器，通过半正焦弦的变化来检测机动，之后切换滤波器，可在短时间内收敛并具有较高的滤波精度。

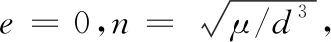
式中：ρ=[xyz]T为轨道坐标系中非合作航天器的相对位置；n为角速度；μ为中心天体引力常数；d为天基平台轨道半径；相对加速度f=fT-fC=[fxfyfz]T，则观测方程为：

式中：Yk为观测矢量；A为偏航角；H为高度角；R为相对距离；εk为已知高斯白噪声；x=[xkykzk]T为航天器轨道坐标系下的位置矢量。

2.2 滤波算法

选取适当的滤波算法，利用自主导航处理测量信息高精度估计轨道信息的核心环节。本文基于扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)[13]，通过融合双滤波及机动检测策略实现高效跟踪估计。

考虑非线性状态方程如下[14]：

xk+1=f1(xk,θk)+Vk

zk=h(xk,θk)+nk

式中：nk～N(0,Rk)为观测噪声。

UKF算法简述如下。

(1)预测过程

构造总数为2L+1的sigma点集：

(i=1,2,…,L)

(i=L+1,L+2,…,2L)

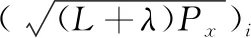
通过状态转移函数f(·)，将sigma点集映射到新sigma点集：

权重公式为：

λ=α2(L+K)-L

其中参数取值：α=10-3，K=0，β=2，加权后的sigma点集用于预测状态的估计值和协方差：

(2)更新过程

通过观测函数h(·)，将sigma点集映射到新sigma点集：

加权新的sigma点集后用于预测观测的估计值和协方差：

状态测量协方差矩阵用于计算卡尔曼增益：

状态更新如下：

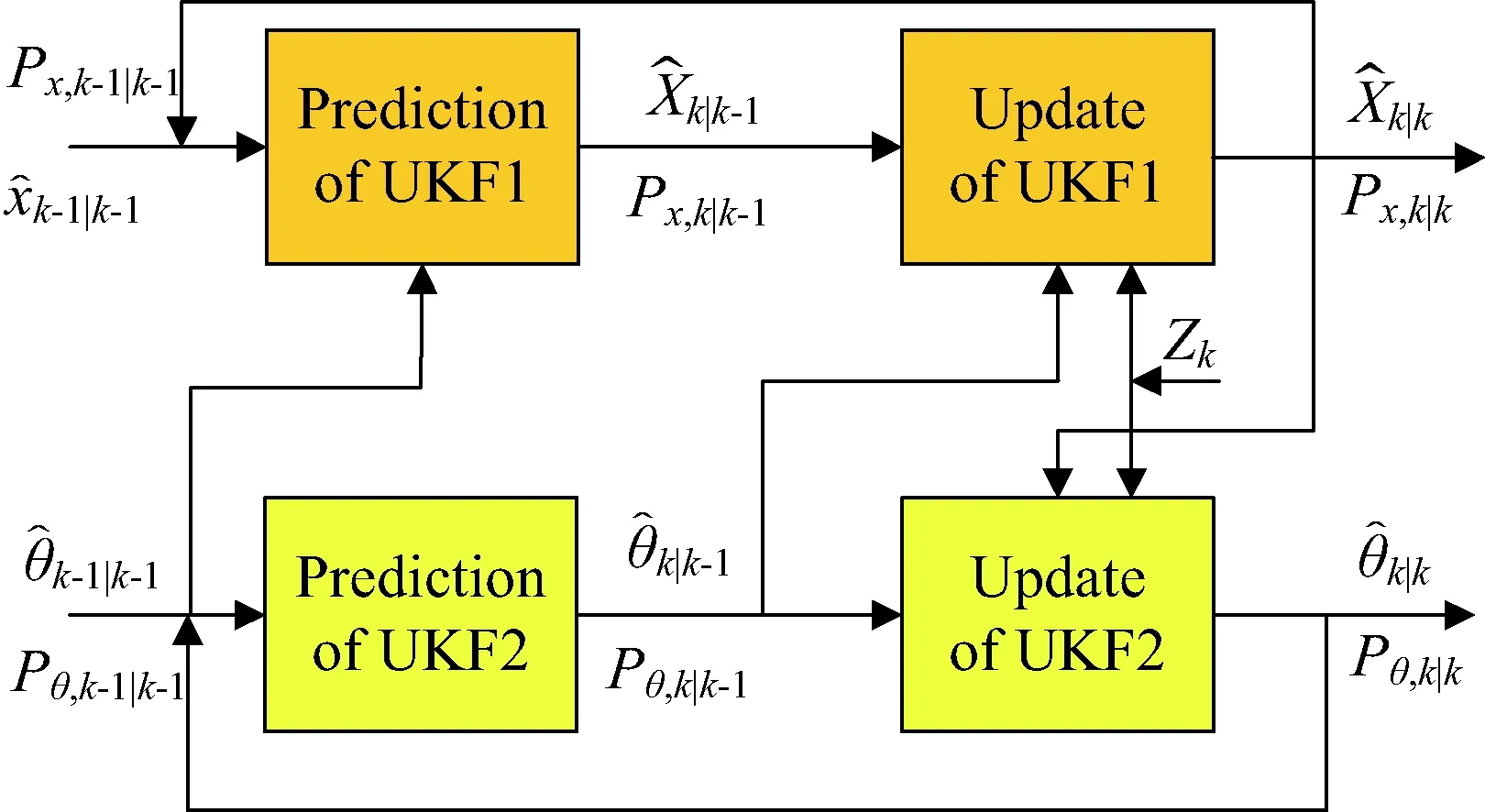
图2 DUKF算法流程Fig.2 The flow chart of dual unscented Kalman filter

UKF1为状态滤波器，UKF2为参数滤波器；x为状态变量，θ为参数变量。DUKF中平行运行2个UKF滤波器，使用相同观测方程，分别用于状态估计和参数估计，且在估计过程中实时校正参数，并对运动状态的估计进行反馈，提升精度。

2.3 基于DUKF的合作目标运动状态估计

对于双重无迹卡尔曼滤波器，其状态滤波器为：

即εk+1=εk+q3。其中，q1、q2、q3均为已知的高斯白噪声。

参数滤波器如下：

式中：q4为已知的高斯白噪声。

观测方程如下：

a=af+asun+q5

式中：q5为已知的高斯白噪声。

对上述状态滤波器，质量m为已知量，由参数滤波器给出；对参数滤波器，反射因子ɛ为已知量，由状态滤波器给出。两个滤波器之间相互配合来提高滤波精度。

2.4 基于半正焦弦机动检测策略的非合作目标运动状态估计

对于非合作目标，在滤波跟踪估计的过程中可能会存在主动且未知机动，导致滤波精度下降甚至会发散。因此需要通过机动检测的手段，来应对随时可能发生的未知机动，故有必要进行非合作目标的机动检测策略的设计[15-16]。

针对轨道动力学非线性的特性，可采用EKF来解决随机连续非线性系统问题[17]。本节在EKF的基础上使用双EKF实现存在一次或多次机动的非合作目标跟踪。脉冲推力产生的机动加速度可表示为[18]：

apulse=Δvδ(t-tc)

式中：Δv为脉冲推力产生的速度变换量；t为机动时刻；δ(t-tc)为tc的冲激函数。

对脉冲推力动力学方程两边求tc-τ到tc+τ的定积分，当τ趋于0时，可得：

rf-ro=0

vf-vo=Δv

式中：下标o表示机动前，f表示机动后。

由此可见，机动前后瞬间目标位置矢量基本不变，而速度矢量有较大变化Δv，且与推力同向。

当非合作目标航天器主动机动后，其轨道根数中变化最为明显的是半长轴a，但轨道根数求解半长轴可能无穷大，因此本文使用半正焦弦p作为特征参数。

图3为椭圆示意图。

图3 椭圆示意Fig.3 Schematic diagram of ellipse

图3中O为极坐标原点，F为右焦点，|OF| =c，椭圆半长轴为a，短半轴为b，M为椭圆上一点(r,φ)，|MF|=r，|FK|=Q。中心天体位于点F处，偏心率e=c/a，由x2/a2+y2/b2=1，当x=c时，y=±b2/a，取正值即为半正焦弦：

p=b2/a=(a2-c2)/a=a(1-e2)

可见，当a和e其中一个变化或二者均变化时，p均会改变。e∈[0,1]，a对p的影响更为明显，对于后续公式(1)中阈值γ选取时要综合考虑以上因素。

当检测到机动时，由于受力改变，仍用原来滤波器进行滤波可能会发散，因此要及时切换到另外一个不同参数的滤波器，再进行后续滤波。空间中的航天器会受到多种因素的干扰，即使无机动时特征参数也会在一定范围内发生小幅度变化，因此设计如下的检测策略。

假设前n1秒无机动，根据这段时间内的半正焦弦估计值统计其均值及方差，代入式(1)。

(1)

当满足式(1)时，表示检测到机动，需要更换滤波器参数继续滤波；不满足时，继续使用原滤波器。为了减少误报，可以设置检测到连续若干点满足上式时表示机动开始。本文设置连续检测到3个点满足上式时，视为机动开始。

此处的双EKF不同于前文的DUKF，前者指的是两个独立的EKF，由于机动前后运动状态发生改变，所需的最优滤波参数一定不同，因此使用两个不同参数的EKF，检测到机动后通过切换滤波器实现短时间收敛。滤波参数指的是初始误差协方差、状态和观测噪声协方差等，不同于DUKF中的参数变量。DUKF的状态方程与状态量和参数量均相关，参数对于状态的估计有很大的影响，若参数变化较大，却把它考虑为一个定值就会使估计结果有很大的偏差，因此使用一个滤波器对参数量进行同步估计、实时校正，通过两个滤波器间的相互嵌套和信息利用对状态估计进行反馈校正，从而提高滤波精度。

3 仿真分析

3.1 合作目标跟踪估计仿真结果

考虑具有连续常推力轨道机动，通过UKF和DUKF实现对于合作目标的跟踪估计。目标航天器初始轨道根数为：半长轴a0=706 300 km，偏心率e0=0.146，轨道倾角i0=30.394/(180π)°，近地点幅角w0=74.373/(180π)°，升交点赤经Ω0=42.790/(180π)°，真近点角η0=45.937/(180π)°，初始反射因子ε0=0.5，航天器初始总质量m0=1 000 kg，常推力10 N。滤波周期设定为T=1 s，仿真时间2 000 s。初始误差协方差矩阵为：

P0=diag[1 1 1 0.01 0.01 0.01 1×10-4]

状态过程噪声协方差矩阵为：

Q1=diag[9×10-18, 9×10-18,9×10-18,

1×10-12,1×10-12,1×10-12, 1×10-4]

参数过程噪声协方差矩阵为：

Q2=diag[1×10-5]

观测噪声协方差矩阵为：

R=diag[3×10-13, 3×10-13, 3×10-13]

模型中存在不确定参数时可考虑使用扩维UKF，即在UKF的基础上把参数也作为状态变量一起进行估计。扩维UKF和DUKF滤波仿真结果如图4和图5所示。

图4 UKF与DUKF的三轴位置估计误差Fig.4 Three-axes position estimation errors using UKF and DUKF

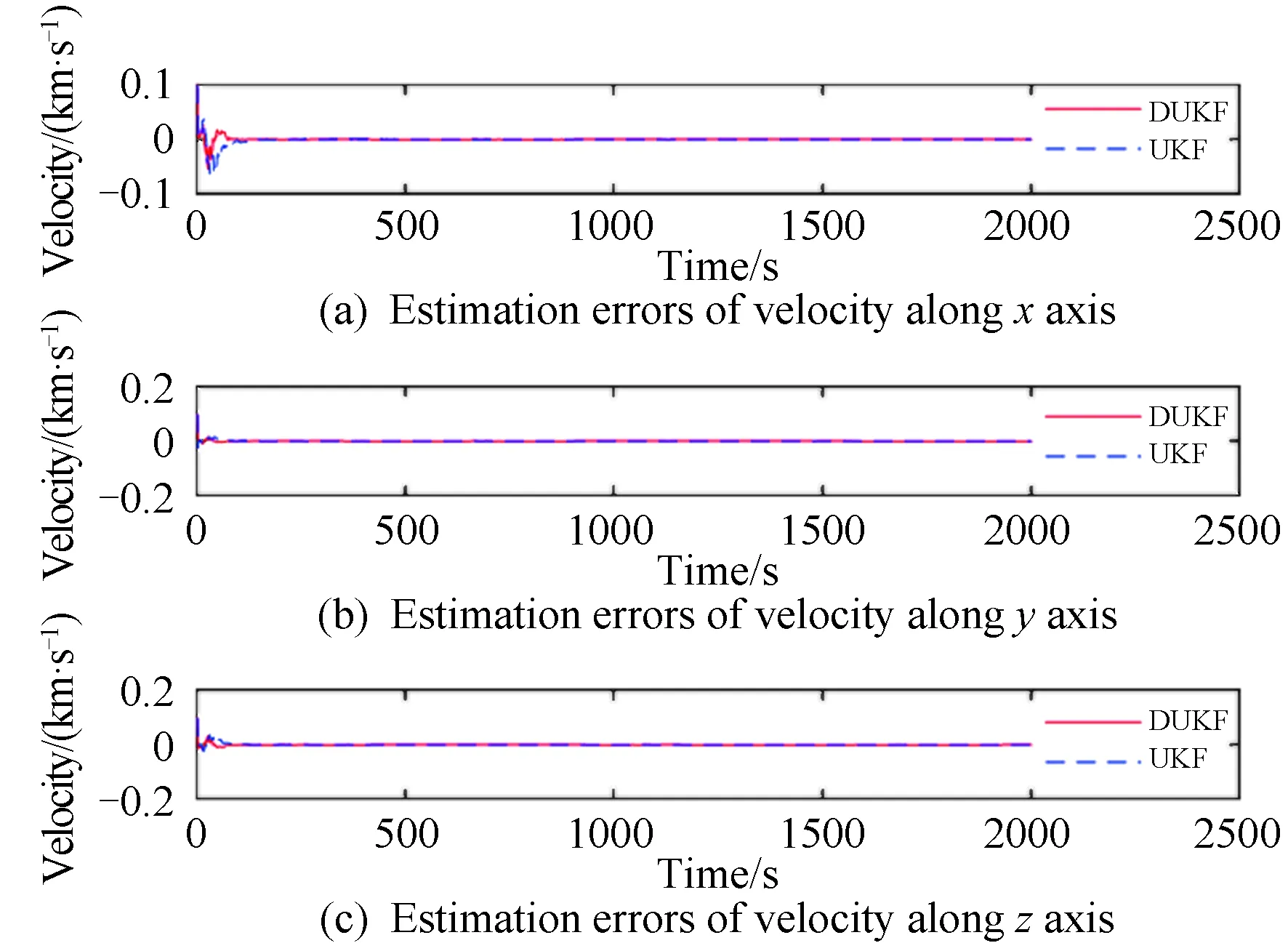
图5 UKF与DUKF的三轴速度估计误差Fig.5 Three-axes velocity estimation errors using UKF and DUKF

图4和图5表明，扩维UKF和DUKF估计的位置和速度均收敛，为了比较两种方法的精度与收敛速度，将x方向的位置误差和y方向的速度误差仿真图放大，如图6所示。

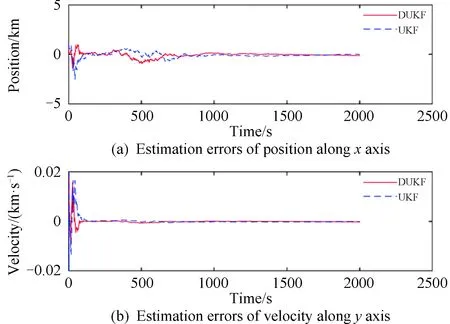
图6 UKF与DUKF在x轴放大的位置估计误差和y轴放大的速度估计误差Fig.6 Magnified position estimation errors along axis x and velocity estimation errors along axis y of UKF and DUKF

扩维UKF最大位置误差约为2.4 km，DUKF约为2.1 km；扩维UKF最大速度误差约为0.02 km/s，收敛时间约为348 s，DUKF约为0.02 km/s和218 s。DUKF相对于扩维UKF收敛更快，因为参数滤波器分担了一部分状态滤波器的工作，降低了其维数，且协同工作使得最大误差值变小，精度提高。从图7可以看出，DUKF对于质量(加速度)的估计收敛更快、精度更高。

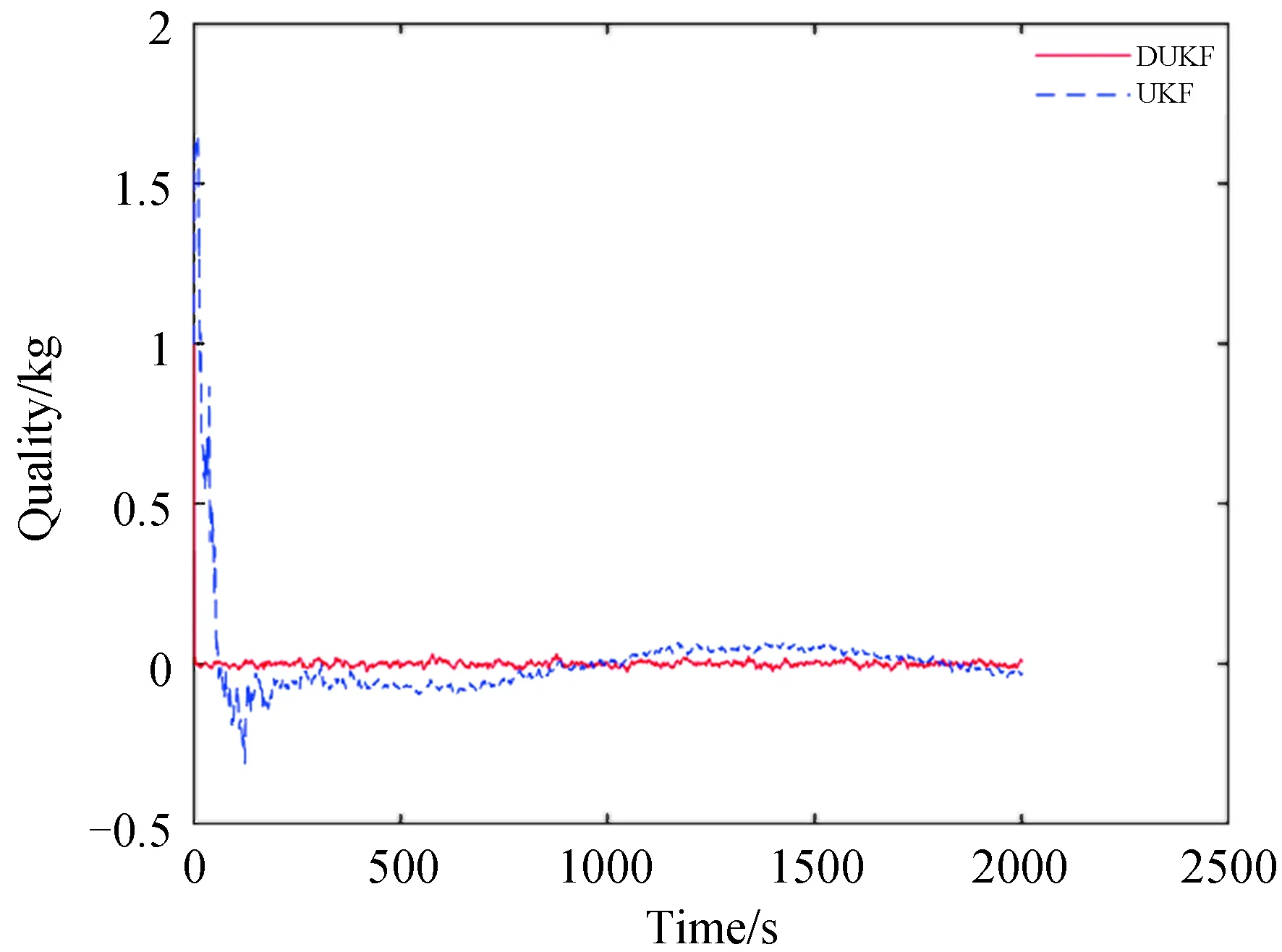
图7 质量估计误差对比Fig.7 Quality estimation errors of UKF and DUKF

综上可知：将质量等因素扩展到原状态量中的扩维UKF滤波方法在理论上更直观，但实际上增加了维数和计算量；DUKF双重滤波算法将状态信息与参数信息进行融合[19]，利用联合密度函数边缘化处理将组合估计问题分解成状态估计子问题和参数估计子问题；且两个滤波器协同运行可有效提高滤波精度。

3.2 非合作目标跟踪估计仿真结果

本节对非合作目标相对导航算法进行仿真。设前200 s无机动，目标航天器分别在501 s、1 001 s、2 001 s处设置机动，大小分别为10-6km/s2、3×10-6km/s2、5×10-6km/s2。天基平台初始轨道根数为：

ac=7 122.30 km，ec=0,ic=(97.750 π/180)°,wc=(311.559 π/180)°,Ωc=(354.829 π/180)°,θc=(160.18 π/180)°。

在天基平台轨道坐标系下，相对位置和速度初值[x,y,z,vx,vy,vz]为：

[0.025,0.025,0.050,-0.388 9×10-3,

-0.439 2×10-3,0.824 6×10-3]

滤波周期设定为T=1 s，仿真时间3 000 s，初始误差协方差矩阵为:

Pk0=diag[1×10-8， 1×10-8， 1×10-8，

1×10-12， 1×10-12， 1×10-12]

过程噪声协方差矩阵为：

Qk1=diag[1×10-14， 1×10-14， 1×10-14，

1×10-16，1×10-16， 1×10-16]

观测噪声协方差矩阵为：

Rk1=diag[1×10-12， 1×10-12， 1×10-8]

切换后的滤波器参数为：

Qk2=diag[1×10-12， 1×10-12， 1×10-12，

1×10-14，1×10-14， 1×10-14]

Rk2=diag[1×10-12， 1×10-12， 1×10-16]

仿真结果如图8、图9所示。将z方向相对位置和速度误差放大，如图10所示。

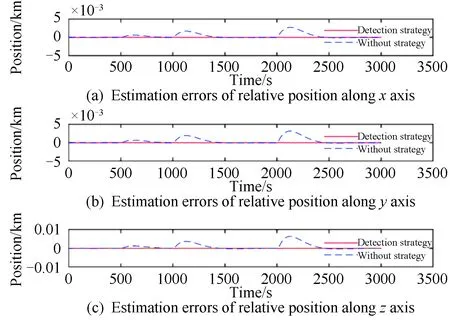
图8 有/无机动检测的相对位置估计误差Fig.8 Relative position estimation errors with and without detection strategy

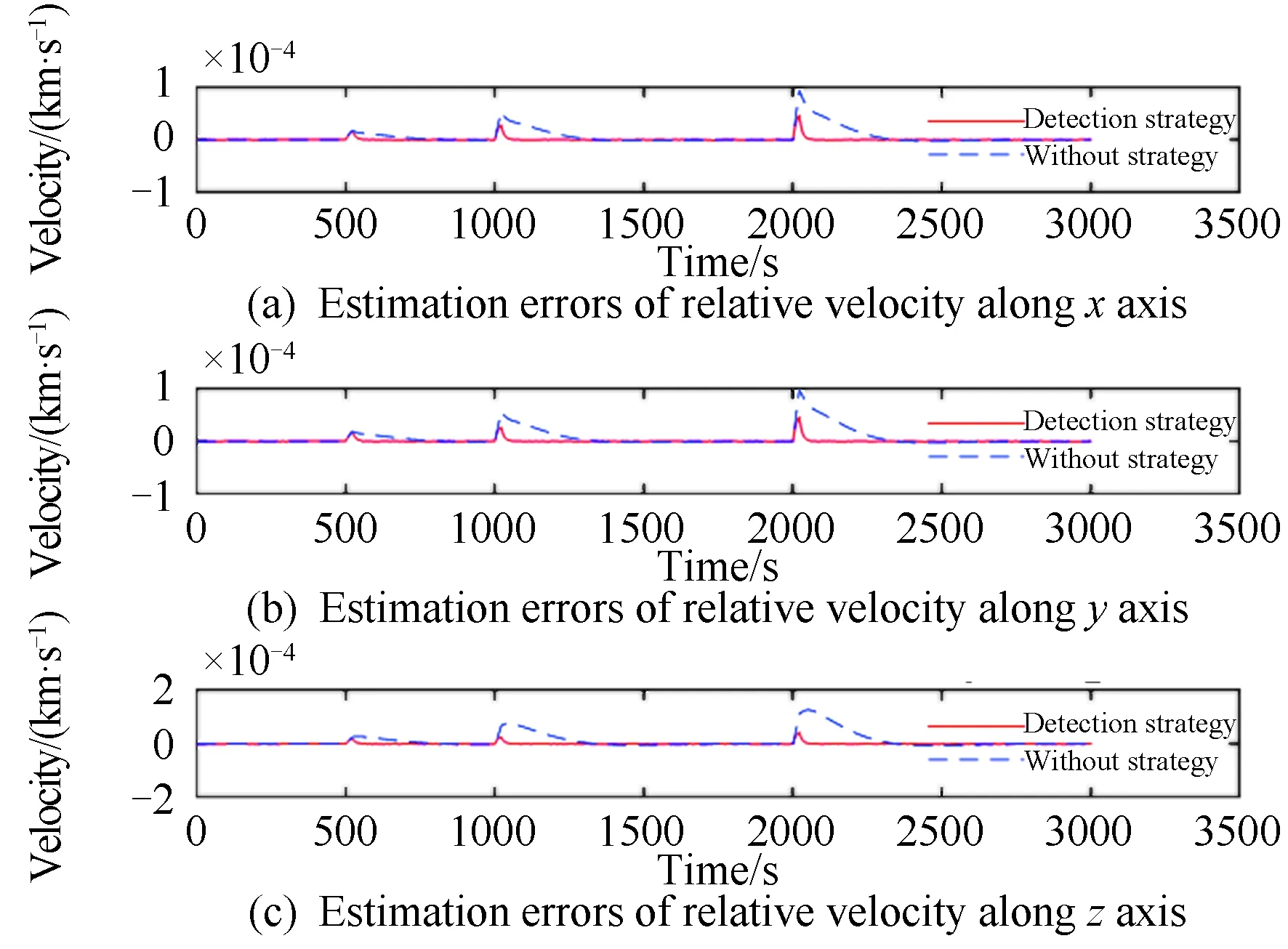
图9 有/无机动检测的相对速度估计误差Fig.9 Relative velocity estimation errors with and without detection strategy

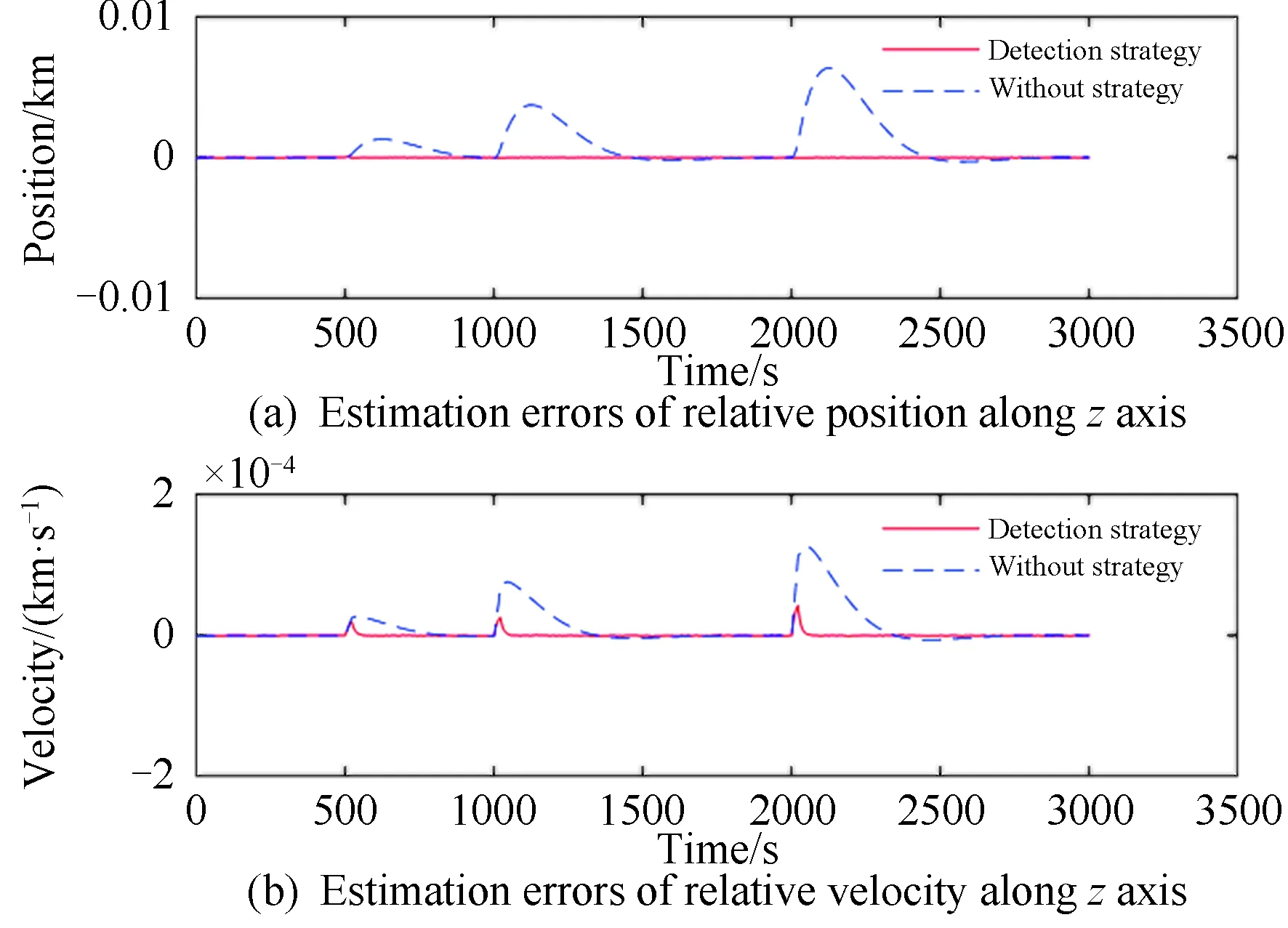
图10 在z轴放大的相对位置和速度估计误差Fig.10 Magnified estimation errors along axis z for relative position and velocity

从图8～图10可以看出，若无机动检测机制，机动发生后滤波器再次收敛速度较慢，约300 s。这是因为机动使航天器的运动状态发生较大改变，原参数无法继续使滤波器达到最优效果，虽然经过较长时间后也能收敛，但在实际工程中可能造成目标丢失。仿真最大相对位置误差约为6.5 m，最大相对速度误差约为0.12 m/s。

在设置机动检测的情况下，分别在500 s、1 000 s、2 000 s左右共检测到3次机动，只需很短时间即可实现机动检测并切换到另一个滤波器后再次收敛，最大相对位置误差约为0.1 m，最大相对速度误差约为0.04 m/s，最大位置和速度误差相比于无机动检测的结果均减小。在3次机动情况下，设置机动检测可保证快速收敛，且滤波精度相比于无检测明显提高。这主要因为机动值变大后，运动状态发生更大改变，无检测策略的滤波算法收敛慢，因此产生较大误差。相比之下，设置机动检测的策略可有效抑制这一点，可以在检测到连续3个超出半正焦弦值统计范围时切换滤波器，由此降低了误报的可能性，保证了滤波跟踪的精度和速度。

4 结论

本文研究了合作与非合作航天器的高精度目标跟踪估计方法。针对带加速度计测量的合作航天器，考虑太阳光压摄动，采用DUKF对其运动状态及质量进行双重估计，实现对目标的跟踪估计；与扩维UKF相比，DUKF获得了更好的滤波精度和收敛速度。针对机动信息未知的非合作航天器，在天基平台轨道系下建立相对运动方程，采用半正焦弦机动检测策略检测机动并切换滤波器，结合双EKF实现目标跟踪估计，其与无检测策略相比，收敛速度更快，精度更高，且可实现多次机动的检测。

本文对非合作航天器的估计是在使用DUKF获得天基平台(合作目标)运动状态的基础上进行的，所采用的基于半正焦弦的检测策略还难以实现对于半长轴和偏心率同时具有较大变化的检测，值得后续深入系统的研究。