古典风险模型中的周期线性 barrier 分红问题
2021-10-25管笑笑
管笑笑
(山东警察学院公共基础教研部,250200,山东省济南市)
0 引 言
古典风险模型最早是由瑞典精算师 Lundberg 于 1903 年提出的.后来,以 Cramer 为首的瑞士学派将其严格化. Gerber 和 Shiu[1]在该模型下提出了Gerber-Shiu 函数;Gerber 和 Shiu[2]研究了该模型的最优分红问题;Dufresne 和 Gerber[3]研究了带扰动的古典风险模型等.
风险理论主要研究和处理保险公司中的破产问题、保费收取原则、再保险策略、随机投资和分红等,并且从定量角度分析保险公司经营的安全性,其中关于分红策略的研究是当前精算界和数学学科研究的热门课题. 常见的分红策略有两种:barrier 策略和 threshold 策略,其中 barrier 策略就是给分红定义一个分红界限b,如果在某个时刻公司的余额大于b,则将超出b的部分立即用于分红,并保持修正余额仍然在b之上,否则没有分红. Gerber 和 Shiu[4]研究了带漂移布朗运动风险模型下的 barrier 分红,为后来分红问题的研究奠定了基础. 关于barrier分红问题的研究可参见文献[5]等. 而后出现了 threshold 策略,即同样给分红定义一个分红界限b,当盈余超过b时对于超出部分将会以一个常数的比例 (分红比例系数大于0小于1) 进行分红,否则不分红. 可参见文献[6]等.
1974年 Gerber 提出了一种分红界限依赖时间的 barrier 策略:线性 barrier 策略,分红界限为b(t)=b+at,如果在某个时刻t公司的余额大于b(t),则将超出的部分立即用于分红,并保持修正余额仍然在b(t)之上,否则没有分红. Gerber[7]讨论了线性 barrier 分红下的古典风险模型及布朗运动,分别推导出了生存概率及分红函数所满足的积分-微分方程,对于分红函数考虑了破产后继续分红和破产后停止分红两种情况,并且得到了索赔服从指数分布时生存概率及分红函数的具体表达式;Albrecher 等[8]在古典风险模型下考虑线性 barrier 分红,研究了分红函数和 Gerber-Shiu 函数;Liu和 Liu[9]在带扰动的古典风险模型下考虑线性 barrier 分红,研究了分红函数和 Gerber-Shiu 函数,得到了索赔服从指数分布时分红函数的具体表达式;刘东海和刘再明[10]讨论了对偶风险模型中的线性 barrier 分红问题.
Albrecher等[11]提出了周期分红策略,该策略与 barrier 策略不同的是只有达到分红时刻并且保险公司的余额超过分红界限时,才能进行分红,这篇文章考虑的是古典风险模型,推导出了平均累积折现分红满足的积分-微分方程,并得到特殊情况下平均累积折现分红的具体表达式;同样 Albrecher 等[12]考虑了带 Brown 运动的模型;Albrecher 等[13]考虑了古典风险模型下的周期分红策略,得到了 Gerber-Shiu 函数的积分-微分方程,并且得到了相应的解;Peng 等[14]研究了对偶风险模型下的周期分红.
在以上文献的基础上,本文研究了古典风险模型下的周期线性 barrier 分红,推导出破产后继续分红W(u)、破产后停止分红V(x,b)及破产概率ψ(x,b)满足的积分-微分方程,并分别求出特殊情况下W(u)和V(x,b)的解.
1 模型介绍
在完备的概率空间(Ω,F,P)中,本节考虑古典风险模型
其中,x∈是保险公司的初始余额,c>0是保险公司单位时间内的平均保费收入,{Yi,i≥1}为独立同分布的非负随机变量序列,Yi表示第i次的索赔额,其分布函数表示为F(y),密度函数表示为fY(y).{N(t),t≥0}是服从参数为λ的 Poisson 过程,N(t)表示到t时刻发生的索赔次数. 假定{N(t),t≥0}和{Yi,i≥1}相互独立. 在此模型中引入线性分红,首先给定一个线性分红限b(t)=b+at,其中b≥0为初值,a为递增速率(0 定义1.1 将保险公司的修正余额定义为R(t)=X(t)-D(t),其中D(t)表示到t时刻为止的累积分红. 第k次观测前的修正余额用R(Zk-)表示,第k次观测后的修正余额用R(Zk)表示. 定义1.2 将保险公司的破产时定义为Tb(t)=Zkb(t),其中kb(t)=inf{k≥1,R(Zk)<0}. 定义1.3 到破产时为止的累积折现分红定义为 其中δ>0为折现因子,(R(Zk-)-b(Zk))+=max{R(Zk-)-b(Zk),0}表示Zk时刻的分红. 定义1.4 到破产时为止的平均累积折现分红即破产后停止分红定义为 V(x,b)=E[D(x,b)|R(0)=x,b(0)=b]. 在风险模型中考虑线性 barrier 策略求解分红函数时,传统的做法是再引入一个破产后仍继续分红的函数W(u),W(u)=Eu[D(x,b)]是单变量u的函数,其中u=b-x,u∈,且有可参见文献[7]. 定义1.5 破产概率定义为ψ(x,b),即ψ(x,b)=P[Tb(t)<∞|X(0)=0,b(0)=b]. 本节讨论W(u)所满足的积分-微分方程及相应的边界条件. 定理2.1W1(u)、W2(u)满足下列积分-微分方程 (2.1) (2.2) 边界条件 (2.3) 证明由于观察过程和索赔来到过程的时间间隔均服从指数分布,且相互独立,所以在充分小的时间段内二者至多只能发生一个.S1表示第一次索赔来到的时刻,Z1表示第一次观测来到的时刻. 考虑在一个充分小的时间段(0,h)内,有下列几种情况发生: (1)在(0,h)内既无索赔也无观测发生; (2)在(0,h)内发生一次索赔,不发生观测; (3)在(0,h)内发生一次观测,不发生索赔. 当u>0时,考虑在一个充分小的时间段(0,h)内,使得u+(a-c)h>0. W1(u)=Eu[D(x,b)]=Eu[D(x,b),S1>h,Z1>h]+Eu[D(x,b),S1 Eu[D(x,b),S1>h,Z1 上式可化为 (2.4) (2.4)式两端同时除以h,再令h→0,即得 (2.1) 式. 当u≤0时,考虑一个充分小的时间段(0,h)内,必然有u+(a-c)h<0,可得 对上式采用类似u>0时的推导,有 (2.2) 式成立. 下面证边界条件. 当u→∞,即b-x→∞,此时公司的余额没有达到分红限,故不会产生分红,即得(2.3)式. 因为一般情况下分红函数在(-∞,+∞)上是连续的,所以我们假设W(u)在0点连续,即 W1(0+)=W2(0-). (3.1) 将u=0+,u=0分别代入 (2.1)、(2.2) 式,又W(u)在0点连续,可得 W′1(0+)=W′2(0-). (3.2) 假设索赔服从参数为β的指数分布,即fY(y)=βe-βy,β>0,y≥0. 对(2.1)式的积分部分做变量替换,令t=u+y,则(2.1)式变为 (3.3) (a-c)W1″(u)-[(a-c)β+(λ+δ)]W1′(u)+δβW1(u)=0. (3.4) (3.4)式解的一般形式为 W1(u)=H1eR10u+H2eR20u, 其中H1和H2为常数,R10和R20为一元二次方程(a-c)R2-[(a-c)β+(λ+δ)]R+δβ=0的根. 两根R10和R20一正一负,不妨设R10>0,R20<0. 由(2.3)式可得H1=0,则 W1(u)=H2eR20u. (3.5) 同理,对(2.2)式的积分部分作变量替换,令t=u+y,得到 (3.6) (a-c)W2″(u)-[(a-c)β+(λ+γ+δ)]W2′(u)+ (γ+δ)βW2(u)+γβu-γβW2(0)-γ=0. (3.7) (3.7)式解的一般形式为 W2(u)=H3eR1γu+H4eR2γu+H5u+H6, 其中H3、H4、H5及H6为常数,R1γ、R2γ为一元二次方程(a-c)R2-[(a-c)β+(λ+γ+δ)]R+(γ+δ)β=0的根. 两根R1γ、R2γ一正一负,不妨设R1γ>0,R2γ<0. 又W(u)线性有界,知H4=0,则 W2(u)=H3eR1γu+H5u+H6. (3.8) -[(a-c)β+(λ+δ+γ)]H5+(γ+δ)β(H5u+H6)=-γβu+γβW2(0)+γ. 比较u的系数得 (3.9) 比较常数项得 (3.10) 由(3.1)、(3.2)式可得 H2=H3+H6, (3.11) R20H2=R1γH3+H5. (3.12) 联立(3.11)、(3.12)式,解得 又 本节讨论V(x,b)所满足的积分-微分方程及相应的边界条件. 定理4.1V1(x,b)、V2(x,b)和V3(x,b)满足下列积分-微分方程 (4.1) (4.2) (4.3) 边界条件 (4.4) (4.5) (4.6) V1(0-,b)=V2(0+,b), (4.7) V2(b-,b)=V3(b+,b). (4.8) 证明证明过程与定理 2.1 类似. 假设索赔额服从参数为β的指数分布,即fY(y)=βe-βy,β>0,y≥0. 对(4.1)式的积分部分做变量替换,令t=x-y,则(4.1)式变为 (5.1) (5.2) (5.2)式解的一般形式为 V1(x,b)=esb(A1eR1γx+A2eR2γx), 其中A1、A2为常数,R1γ、R2γ为一元二次方程cR2+[cβ-(λ+γ+δ)+as]R+[as-(γ+δ)]β=0的根. 当s<0时,两根R1γ、R2γ一正一负,不妨设R1γ>0,R2γ<0. 由(4.6)式可得A2=0,则 V1(x,b)=A1esbeR1γx. (5.3) 同理,分别对(4.2)、(4.3)式的积分部分作变量替换,令t=x-y,得到 (5.4) (5.5) (5.6) (γ+δ)βV3(x,b)+γβ[x-b+V(b,b)]+γ=0. (5.7) (5.6)、(5.7)式解的一般形式分别为 V2(x,b)=esb(B1eR10x+B2eR20x), (5.8) 其中B1、B2为常数,R10、R20为一元二次方程cR2+[cβ-(λ+δ)+as]R+(as-δ)β=0的根. V3(x,b)=esb(C1eR1γx+C2eR2γx)+C3x+C4b+C5, 其中C1、C2、C3、C4及C5为常数,R1γ、R2γ为一元二次方程cR2+[cβ-(λ+γ+δ)+as]R+[as-(γ+δ)]β=0的根. 根据V(x,b)的线性有界性,知C1=0,故 V3(x,b)=C2esbeR2γx+C3x+C4b+C5. (5.9) [cβ-(λ+γ+δ)]C3+aβC4-(γ+δ)β(C3x+C4b+C5)=-γβx+γβb-γβ(C3b+C4b+C5)-γ. (5.10) (5.11) 比较常数项,有 [cβ-(λ+γ+δ)]C3+aβC4-(γ+δ)βC5=-γβC5-γ,则 (5.12) 根据 (4.7)、(4.8)式有 A1=B1+B2, (5.13) B1e(R10+s)b+B2e(R20+s)b=C2e(R2γ+s)b+C5. (5.14) 将(5.3)、(5.8)及(5.9)式代入(4.4)、(4.5)式,得 (cR1γ+as-γ)A1-(cR10+as)B1-(cR20+as)B2=0, (5.15) (5.16) 根据A1、B1、B2及C2的4个方程 (5.13)~(5.16)式可解得A1、B1、B2和C2的值, 在本节中,讨论破产概率ψ(x,b)所满足的积分-微分方程及相应的边界条件. 定理6.1ψ1(x,b)、ψ2(x,b)和ψ3(x,b)满足下列积分-微分方程 满足边界条件 证明证明过程与定理 2.1 类似. 本文在古典风险模型下讨论周期线性 barrier 分红,分别得到破产后继续分红,破产后停止分红以及破产概率所满足的积分-微分方程,并分别推导出特殊情况下破产后继续分红和破产后停止分红的具体表达式.2 破产后继续分红

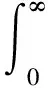
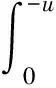





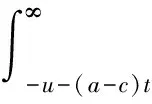
3 索赔服从指数分布时W(u)的求解

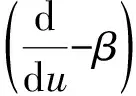

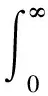
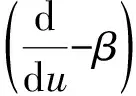


4 破产后停止分红
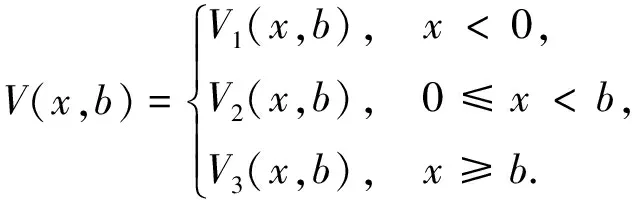
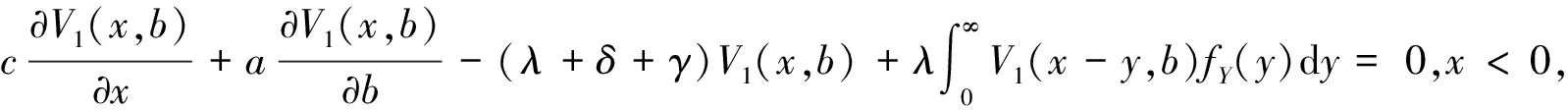
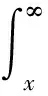
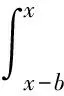
5 索赔服从指数分布时V(x,b)的求解
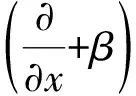


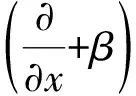
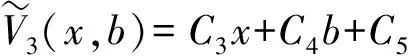

6 破产概率ψ(x,b)

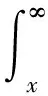

7 总 结
