PWGL音高形态算法作曲技术初探

罗 超

引 言

在现代音乐的创作中，计算机已经成为许多人创作中必不可少的工具之一。在计算机音乐作品的创作中，对于各种软件和硬件的使用，在相当大的程度上影响一个作品的风格和形态。

目前，作曲家们使用比较频繁的关于计算机音乐创作的软件有Max/Msp、Pd和PWGL等等，其中PWGL（Patch Work Graphical Language，即“PatchWork图形化语言”），是一个建立在Common Lisp、CLOS（Common Lisp Object System）和OpenGL基础上的交互性视觉化编程环境。国内首次接触到PWGL是在2009年10月举行的上海国际电子音乐周，由国际作曲家机构PRISMA①在工作坊活动中对PWGL进行介绍和交流。目前，随着PWGL平台的不断拓展，各种构件功能的完善化和规则使用的方便化，使越来越多的人通过这个平台来完成自己的作品创作。本文所讨论的一切算法作曲的规则和应用，都依托于PWGL这个平台。

基于形态学的理论基础，当我们把音乐中的音乐材料抽象的提取出来，对应在函数关系图中，就会得到相关的形态曲线。本文研究的主体为横向的单线条音高，当其通过某些函数关系式，一个或几个变量取一定的值时，另一个变量有唯一确定值与之相对应，并表现在函数关系图中形成曲线，这就是本文广义上的音高形态。而狭义的音高形态，指的是音高通过PWGL的计算，分析产生出来的新鲜值曲线与能量值曲线，这是本文分析的主要内容。

一、相关算法工具

（一）New-old-analysis构件

以小字一组e、f、g、f、e作为探测对象。为确保每一个音能够计算出正确的数值，现将音符依次对应为a、b、c、b、a，并且在头尾处添加X、Y，以方便计算，形成：X、a、b、c、b、a、Y。以1为起始值，每一次新字符的出现，则数字往后递增，遇到重复的则记为之前所标记的数值，得出数列1（图1左）；再对相邻的数值进行求差值，必须是后者减去前者，所得两者间的数列差，为数列2（图1右）。

将数列1的原始数值，以行为单位，横向相加，得到数列3（图2左）；再将数列2的数值，以行为单位，与数列3同行的数值相乘，得到数列4；再对每一纵列进行求和值，得到所举出音列（e、f、g、f、e）的新鲜值（图2右）：20、33、44、-35、5。

图2

（二）Energy-prof-morph-analysis构件

意大利作曲家雅各布在武汉音乐学院的多次交流活动中，都提到了“Energy”能量这个词。在他举办的工作坊中，向大家交流了在PWGL平台上对音乐作品能量的分析，这能让每个分析者都能够更加全面与客观地通过数值来掌握作品中音乐能量的分布关系以及运动趋势。

在PWGL平台中，Energy-prof-morph-analysis构件译为能量形态曲线分析，通过对音高的能量值分析，在函数关系图中形成曲线，构成音高形态中的能量值曲线，此构件同样是由意大利作曲家雅各布通过lisp语言编写而成的。Energy-prof-morph-analysis构件的运算过程如下：

此构件运算的前提，是建立在上文介绍的音符新鲜值（数列4）基础上，添加上首尾的X与Y字符，形成X、a、b、c、b、a、Y，对数列4进行绝对值求值，得到数列5：（0）、20、33、44、34、5、（69）。再对数列5中相邻的数值进行求差值，必须是后者减去前者，所得两者间的数列差，得到数列6；再对数列6进行绝对值求值，得到所举出音列（e、f、g、f、e）的能量值：20、13、11、10、29。

二、音高形态的新鲜值曲线和能量值曲线

（一）音高新鲜值关系曲线

在PWGL中，每一个构件均不识别音高、节奏、和声等音乐要素，因此，在分析乐谱之前，必须用特定的运算原则对其进行转换，使音符能够被构件所识别，从而实现其数据信息的分析和计算。

刘莉、李洪等寄存处的工作人员全部被带到站前派出所值班室，邢慧负责询问刘莉，刘莉还在瑟瑟发抖，回答前言不搭后语。而询问李洪的刘志武同样也没有得到什么有用的线索，刘志武问：“根据你们的台帐记录，当时是你接待的，你再想想，对方是一个什么样的人，男的或者是女的，高矮胖瘦？”李洪说：“我们每天少说有几百人来寄存，我们哪注意来寄存的是谁啊，我们都只认牌子不认人。”

这首作品产生于作曲家的十二音序列主义体系诞生之前的探索时期。在这首作品里，能较明晰地发现作曲家对于调性的模糊处理：虽然没有使用严格意义的十二音技术，但与其更早的作品相比，已经极大程度上脱离了调性写作的束缚，并已初步具备“用十二音作曲”的思维。如果把谱例中的上方声部的音高依次排列，可以发现这首作品在“用十二音作曲”发展过程中所具有的实验性，以及为突破调性和建立新规则的尝试。这首作品所使用的十二个音，如表1：

表1

如前所述，为使PWGL能够识别不同的音高并进行运算，我们需要将上图所示的音列进行转换：中央C（c1）为60，相邻的音则相应的递增或递减一个数值，以此类推，下面列举出5个八度音域内的各音所代表的数值，如表2：

表2

通过表2，我们可以得到谱例1音列所对应的数列：

77、81、77、70、73、72、83、69、73、76、75、63、66、67、65、74、72、66、68（重复音均加粗）

根据图表转换出来的数列，在PWGL中构件运算得到的新鲜值曲线，如图3：

图中，X和Y轴，分别代表时间与新鲜值。圆圈标识的音是在新音之后出现的重复音；三角形标注的音是在非新音之后出现的重复音。由图，我们可以看到，新音之后的重复音都获得低于零值的新鲜值，而非新音之后的重复音，则获得了较高的新鲜值。

《抒情组曲》共有六个乐章，这是贝尔格运用十二音技创作的第一部作品。第一乐章在音高材料的组织上包含运用十二音序列技法与自由无调性技法两种类型，谱例2是其基本序列完整呈示的3个小节。

通过表2，我们可以得到谱例2中音列所对应的数列：

65、64、72、69、79、74、80、74、74、74、75、66、70、59、60

通过在PWGL中构件运算得到的新鲜值曲线，我们可以看到，新音之后出现的重复音都获得了低于零值的新鲜值，而在非新音之后出现的重复音，则获得了高于或等于零值的新鲜值。

通过对大量音乐作品实例的新鲜值曲线分析与研究，我们可以看到：

在新音之后出现的重复音，它将获得较低的新鲜值（低于或等于0值）。

当重复音b的前一个音a也为重复音时，b的新鲜值高于或等于零值，具体的数值高低取决于前一个音符a的新鲜值的高低：前一个音符a的新鲜值越低，则b的新鲜值会相应的越高。

3、当某音出现重复时，重复音与被重复音之间的新鲜值之差与两者间隔的时长成正比；当a与其重复音a’相距时值越长，两者获得的新鲜值之差也就越大；一般情况下，重复音的新鲜值要低于被重复音的新鲜值，当重复音的前一个音为非新音（重复先前的其他音）时，将改变这个现象。

（二）音高能量值关系曲线

在PWGL的Energy-prof-morph-analysis构件中，每一个音的能量值均可以通过计算得出。我们可以根据能量值的分布曲线图，观察音乐中一定时间内的音符的能量值大小，通过对音高形态的能量值曲线图，完成对音乐作品发展动力上的把握，让其音乐主旨表现得更加淋漓尽致。下面，通过对经典音乐作品的旋律线条的分析，来寻找能量值曲线分布与音乐发展动力之间的关系。

通过表2，我们可以得到谱例3中音列所对应的数列：

谱例3：Beethoven，Violin，Sonata No.5 in F Major，Op.24

70、72、70、69、70、82、79、77、76、76、77、76、75、76、86、84、84、82、81、79、77、78、79、81、82、71、72、74、76、77

通过在PWGL中构件运算得到的能量值曲线，我们可以看到，最后2小节获得了最大的能量值，能量值的动态范围也是最大。当我们回到谱面进行分析的时候，会发现在最后两小节#F音和B音的出现，打破了主调F大调的稳定性，产生了新的音乐色彩和听觉感受。对于不识别音高的PWGL运算程序来说，这也印证了其分析结果与实际音乐效果的一致性。

通过表2，我们可以得到谱例4中音列所对应的数列：

65、68、70、66、66、59、58、59、61、63、64、65、67、69、69、70、72、67、63、63、63、62、62、62、63、66、66、62、63、65、66、68、70

在PWGL中构件运算得到的能量值曲线，如图4：

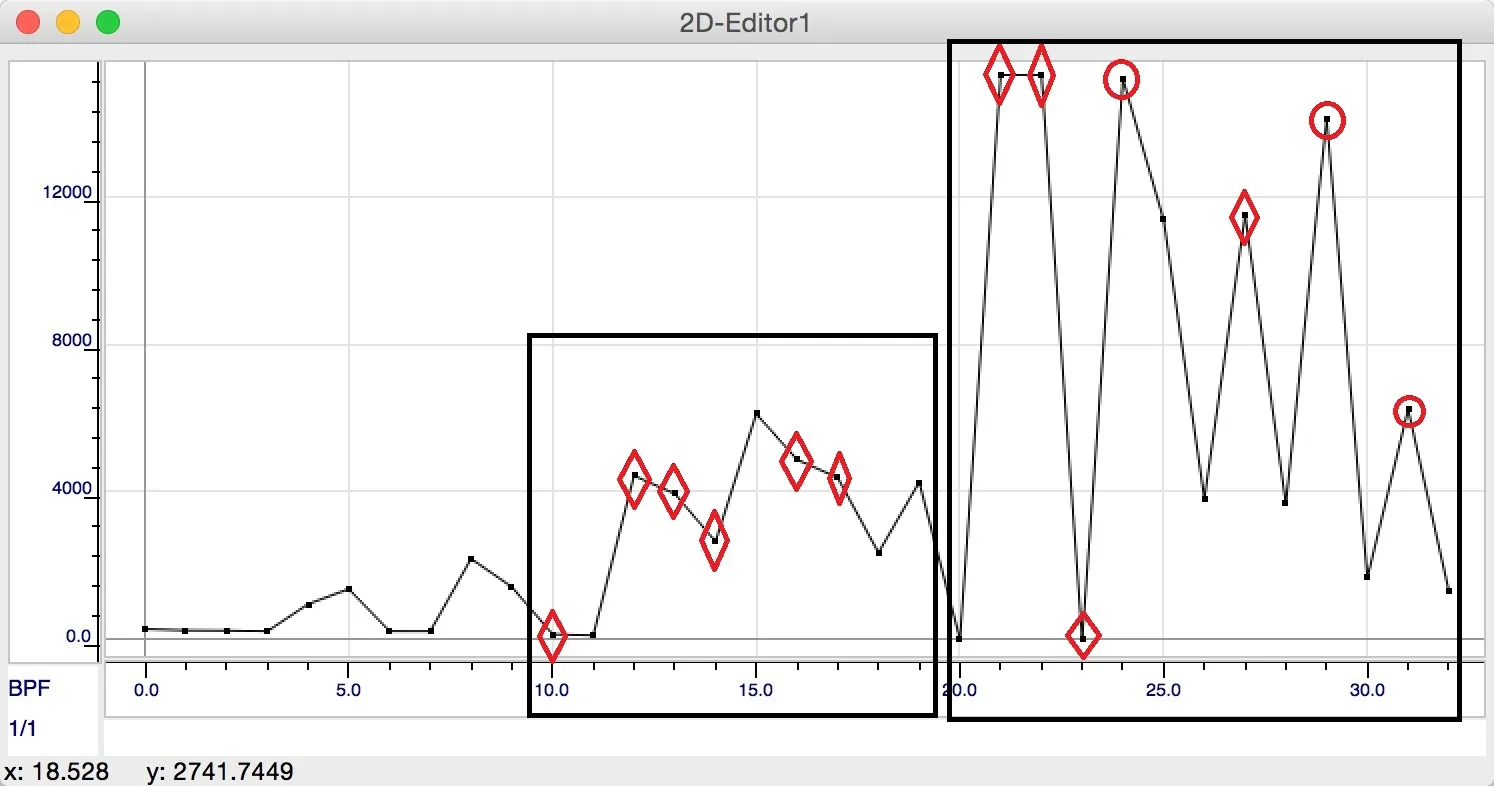
图4：菱形标注的是临时变化音，圆圈标注的是个别重复音

通过上图，我们可以很清楚的看到，在两个方框区域内的能量值动态范围是比较大的，第二个方框内的能量值不仅动态大，而且出现了能量的最大值。

通过调性分析，我们可以得知，两个方框区域内正是音乐转调的位置，为什么两处同是转调而动态变化范围会有如此差别？这是因为重复音的存在。第二个框内，除了菱形标注的峰值外，其余峰值均为重复音。对于连续的同音反复，当次数大于或等于3次时，能量值将变的更低，甚至不具有能量值；当其他的音出现在同音反复的音列时，其之后的音将获得较高的能量值。

我们可以在该谱例的第7-8小节（63、63、63、62、62、62、63）的基础上，扩大同音反复的次数（63、63、63、63、63、62、62、62、63、63、63）来观察这一现象。通过能量值曲线分析，我们可以得出，关于同音反复：第二次同音反复能量值基本保持；第三次以后的同音反复值降到最低，甚至为零值；当同音反复a中加入新音b后，将破坏其能量值的变化规律，导致新音b后的同音反复a的能量有所回升（大于零值）。

通过对大量音乐作品实例的能量值曲线分析与研究，我们可以看到：旋律音高中的临时变化音出现越密集的区间，能量值曲线的动态越大，并且出现能量值的最高点。这与谱例实际的调性情况相一致，当变化音出现的越频繁的时候，是调性越不稳定的时候（如图4方框区域），这一点很重要。以此为基础，我们就能够在更大的空间内，通过音高形态的控制来实现我们对音高本身的控制，而不仅仅局限在调性音高的音符本身上。调性的游移产生色彩的变化，稳定调性结构的逐渐瓦解，让音乐获得了不断向前发展的动力，这时往往也是音乐能量比较高的地方。音乐家们也常常通过这样的手段，来推动音乐达到高潮。从听众的聆听角度看，一般这些地方也是最令人印象深刻的地方。

结 语

随着算法作曲技术的进一步发展，在某些风格的作品创作中，旋律性音高概念将会进一步弱化；而随着PWGL越来越完善的运算构件，它将被更多的音乐创作者所接受和使用。本文在形态学的理论基础上，通过对PWGL中新鲜值构件与能量值构件运算过程的剖析，以及在音乐作品实例中的具体分析，将音乐中音高所承载的信息转化为直观的曲线形态，为音乐家的创作提供具有一定准确性和实用性的数据支持。

本文通过对大量音乐作品的分析，得到了音高在新鲜值曲线与能量值曲线中的一般规律，希望能够对有意使用PWGL平台算法作曲技术创作者们，提供一些具有参考价值的信息。这仅仅是一个开始，希望在未来时间里，不断地完善与补充，并且对两者之间的关系做更深层次的研究，使之能够更加全面的显露其中纷繁复杂的关系。但就目前来说，本文所得出的结论是具有相对正确和可具参考性，也是具有现实意义的。■

注释：

① PRISMA是一个国际间作曲家自发成立的一个组织，目的在于学科知识的整合，以及研究成果的交流和发布。PRISMA每年定期举行学术论坛，使得成员之间对各自新成果，进行内部间的沟通和完善，从而发布给世界各地的音乐人们所应用。雅各布·巴博尼-施林吉（Jacopo Baboni-Schilingi）意大利作曲家，是国际作曲家机构PRISMA创办人，本文所举例的PWGL的规则构件也是由他进行创作编写的。