Fixed-time position coordinated tracking control for spacecraft formation flying with collision avoidance
2021-10-25MingleiZHUANGLiguoTANKehngLIShenminSONG
Minglei ZHUANG ,Liguo TAN ,Kehng LI ,Shenmin SONG
a Center for Control Theory and Guidance Technology,Harbin Institute of Technology,Harbin 150001,China
b Research Center of Basic Space Science,Harbin Institute of Technology,Harbin 150001,China
c Science and Technology on Space Intelligent Control Laboratory,Beijing Institute of Control Engineering,Beijing 100190,China
KEYWORDS Collision avoidance;Disturbance rejection;Fixed-time stability;Sliding mode control;Spacecraft formation flying
Abstract In this paper,the fixed-time stability of spacecraft formation reconfiguration (position tracking)is studied.Firstly,a novel nonsingular terminal sliding mode surface is designed and based on which a fixed-time coordinated controller is designed to keep the closed-loop system states have a finite settling time bounded by some predefined constants.Secondly,another nonsingular terminal sliding mode surface is designed by combining the artificial potential function and the aforementioned sliding surface,which meets the mutual distance constraint during transition process among spacecraft when it is bounded.Then another coordinated controller with fixed-time observer considering mutual distance constraint is presented,which guarantees the closed-loop system states stable also in bounded settling time.Finally,simulation results are shown to validate the correctness of the proposed theorems.It is worth mentioning that the control schemes also work even though there is a properly limit on the control input.
1.Introduction
During the past decades years,Spacecraft Formation Flying(SFF) has been an important technique in advanced space applications such as earth observation,high-resolution,and deep-space exploration.Different SFF tasks,such as Techast-21,GRACE,and PRISMA,have been proposed.1To accomplish above missions,the different members of SFF have to keep track of their desired positions in the reference coordinate system for making a particular formation.However,the high nonlinearity,the time varying disturbance and the uncertainties of the spacecraft dynamics make the controller design more difficult.So,there are still challenges for designing high performance controllers for SFF.
With respected to SFF,coordinated control is one of the most important technique and primarily related to attitude coordination and formation coordination.Based on formation defined as a pair of spacecraft,2–4proposed coordinated controllers to handle external disturbance,model uncertainties,actuator saturation,and actuator fault,respectively.To solve the coordination problem of multiple spacecraft,many controllers were proposed,5–10which were used to handle the uncertainties and the absence of velocity measurements,and the communication delays.
However,the aforementioned proposed controllers can only keep the states of closed loop systems asymptotically converge to origin.To make a higher control accuracy and faster convergence rate,finite-time control theory has attracted more and more attention which also provides strong robustness to external disturbance and system uncertainties.Terminal Sliding Mode (TSM) control theory is one of the most important branches of finite-time control theory.In Ref.11,a finite-time attitude coordinated controller was designed without needing the information of any angular velocity.In Ref.12,a finitetime distributed orbit synchronization controller was proposed,which solved the problem of unknown external disturbance and communication time delay.In Ref.13,two finitetime coordinated formation flying controllers were proposed with the external disturbance taking into account.There is also other control theory make the closed loop system states stable in finite-time such as homogeneous theory.In Ref.14,a finite time coordinated attitude controller was proposed for multiple spacecraft.In Ref.15,a finite time relative position coordinated tracking controller based on homogeneous theory was proposed without considering velocity measurements.
However,the actual time that system states converge to origin is dependent on initial conditions when the finite-time controller is adopted.The settling time of different initial states varies greatly.To overcome this drawback and improve the robustness to initial conditions,the fixed-time concept was firstly proposed by Cruz-Zavala et al.,in Ref.16.Then the fixed-time stability of nonlinear systems was studied by Polyakov.17A new TSM controller was designed for second order nonlinear systems by Zuo18to keep its fixed-time stability.A novel fixed-time TSM surface was designed by Corradini and Cristofaro.19As for spacecraft,there are rare works about fixed-time stability.In Ref.20,a finite-time controller was proposed to guarantee the closed loop system stable in the sense of fixed-time concept.In Ref.21,a fixed-time anti-unwinding controller was designed such that the desired attitude can be tracked with bounded convergence time.A fixed-time decentralized coordinated controller for multiple spacecraft attitude systems was proposed based on TSM control theory in Ref.22.A fast TSM tracking controller with adaptive laws was designed in Ref.23 to guarantee the closed loop system fixed-time stable.By enumerating the above articles,one founds that the current research is mainly aimed at spacecraft attitude,and there is almost no research about the fixed-time stability of position coordinated control of multiple spacecraft.
The other important issue about multiple spacecraft formation reconfiguration (position tracking) is the collision avoidance constraint during the transition process especially when the desired position between each member is very close.Artificial potential function(APF)method is one of the most useful technique to handle collision avoidance problem.It has been widely studied by combining it with other control methods.In Ref.24,an asymptotically stable controller was proposed for multiple spacecraft to avoid obstacles and maintain the formation configuration.An asymptotically tracking control scheme was presented for SFF decentralized collision avoidance scheme in Ref.25.There are also other similar works such as Ref.26–28.A collision free distributed controller was designed for six-DOF SFF based on dual quaternions in Ref.29.A robust finite-time TSM controller was designed in Ref.30 to handle the relative position tracking and attitude synchronization control problem with collision avoidance and changing network topologies.In Ref.31,the target enclosing control problem considering collision avoidance and time varying communication topology was studied,the controller was designed based on APF and sliding mode observer.A distributed finite-time formation tracking controller was designed by Huang in Ref.32,which was assembled by finite time observers and APF.As for the research of fixed-time stability about spacecraft formation reconfiguration considering mutual distance constraint,there is almost nothing works about it.
In this paper,the fixed-time stability about SFF reconfiguration (position tracking) is studied.Two fixed-time coordinated controllers are designed based on sliding mode control to handle the external disturbance and system uncertainties.The main contributions are stated as follows:
(A) A novel TSM surface is designed which keeps the system states converge to origin with bounded convergent time after the sliding surface reaches to zero.Then,a revised form of the designed TSM surface is presented which is nonsingular.Finally,an adaptive fixed-time controller is proposed to keep the fixed-time stability of tracking error and velocity error.
(B) To satisfy the constraint of mutual distance among each member,a new TSM surface is designed by subtly combining the aforementioned nonsingular TSM surface with an APF.The new designed TSM surface guarantees the system states converge to origin in bounded settling time after the sliding surface reaches to zero.The boundedness of sliding surface also guarantees the boundedness of the APF,then the mutual distance constraint is satisfied.A fixed-time observer is designed to handle system uncertainties.Finally,a fixed-time coordinated TSM controller is proposed to not only meet the mutual distance constraint but also keep the closed loop system states stable.The proposed control scheme is free of local minima.
(C) Rigorous proofs are obtained by Lyapunov stable theory and simulation results validate the correctness of the proposed theorems.
The rest of this paper is organized as follows.In Section 2,SFF dynamics and some preliminaries are investigated.In Section 3,the nonsingular TSM surface is designed and the fixedtime coordinated controller is developed which can handle external disturbance.In Section 4,firstly,the APF used in this paper is addressed;then a new nonsingular TSM satisfying mutual distance constraint is designed;finally,a fixed-time coordinated controller is proposed.In Section 5,numerical simulation results are presented to validate the rightness of the proposed theorems.This paper ends with conclusion and suggestion for further work.
2.SFF dynamics and preliminaries
2.1.SFF dynamics
In this subsection,the nonlinear relative model of SFF is introduced and each spacecraft is assumed to be a rigid body.The reference orbital coordinate system is denoted bywith its origin at the centroid of the reference spacecraft.TheXraxis is along to the local vertical,theYraxis is along to the local horizontal,andZraxis can be obtained according to the right-hand rule.The reference spacecraft is a standard used to describe the relative positions in formation flying.In this paper,the reference spacecraft is not a real spacecraft,and it can be regarded as a virtual spacecraft running on a particular orbit.

the true anomaly of the reference spacecraft,rr=‖rr‖ is the distance between the center of reference and the Earth’s center,μEis the gravitational constant of the Earth,miis the mass of theith spacecraft,diis the external disturbance vector,uiis the control force of theith spacecraft,is the distance between the centroid ofith spacecraft and the Earth’s center,i=1,2,∙∙∙,n,wherenis the total number of the spacecraft in formation.The spacecraft relative model mentioned above has high accuracy and is adaptive to any eccentric orbits when the distance between the spacecraft and the reference is not very far.
Letρidbe the desired position of theith spacecraft,then the position error of theith spacecraft isei=ρi-ρid.The position error dynamics is defined as follows.
2.2.Graph theory
The information exchange among spacecraft is described by weighted undirected graphs.Each spacecraft is regarded as a node,then the set of nodes is defined asN={1,2,∙∙∙,n},the set of edges is defined as ζ=N×Nand the weighted adjacency matrix is defined asA=[aik]∊Rn×n.ThenG={N,ζ,A}is used to represent the weighted undirected graph.The information transfer fromkth spacecraft toith spacecraft is denoted as(i,k),then(i,k)∊ζ.In an undriected graph,the element ofAis defined asaik=aki>0,ifi≠k.Otherwiseaik=0.If any two nodes are reachable,the undericted graph is supposed to be connected.The degree matixDis defined asD=diag[d1,d2,∙∙∙,dn],whereThenL=D-Adenotes the Laplacian matrix.
2.3.Notations and relative lemmas

2.4.Control objective
The control objective of this paper is to design coordinated controllers such that the formation reconfiguration under undirected communication topology can be completed in fixed-time.
3.Robust fixed-time coordination control law design
In this section,the detailed procedure of implementing fixedtime coordination controllers is presented.For no consideration of collision between spacecraft in formation,a fixedtime controller is proposed based on a new designed TSM surface.
Before implementing the controller design,the position error betweenith spacecraft andkth spacecraft is defigned as follows.

In terms of defination of weighted underited graphGand the Laplacian matrixL,the lumped position errorof theith spacecraft is defined as follows.

3.1.Fixed-time TSM surface design

Theorem 1.For the SFF error dynamics system Eq.(3),the achievement of a sliding motion on si,j=0guatantees the robust finite-time sabilization of the system.Once the sliding manifold has attained,the states reach the origin within fixed-time Ts.And the control input shows no singularity.


Remark 2.The proposed TSM surface Eq.(12)is nonsingular and it also guarantees the system states converge to zero in fixedtime after the sliding manifold is established.
3.2.Robust fixed-time coordinated controller design without collision avoidance
In this subsection,the fixed-time coordinated controller will be designed to make each follower simultaneously track its own desired position.
Assumption1.The external disturbance satisfiesandmaxand l are positive constants.
To facilitate the design of the coordinated controller,the compact forms of the vectors are defined:



Remark 4.The controller Eq.(16)has some parameters to be set when applying it.k1andβaffect the amplitude of TSM surface and the boundary of settling time,εaffects the amplitude of control input and the control accuracy.k2,k3,α1andγ1affect the boundary of reaching time and the amplitude of control input,and the constraintα1+γ1=2should be satisfied.k4and k5are used to handle system uncertainties,they shoud satisfy the cooresponding constrants(one can find them in the proof pro-cess).υi is used to adjust the value of

Fig.1 The communication topology among spacecraft.
4.Robust fixed-time coordination controller design with collision avoidance
In this section,the fixed-time stability of SFF reconfiguration considering mutual distance constraints will be stated based on APF and sliding mode control.A novel TSM surface is proposed by combining the aforementioned TSM surface Eq.(12) and the gradient of APF,which also keeps the fixedtime stability of SFF.And the local minima problem of APF is also solvable with the new designed TSM surface.Then a fixed-time observer is designed to handle the system uncertainties and external disturbance.Finally,a controller is proposed.

Fig.2 TSM surface Eq.(14) of every follower in SFF.

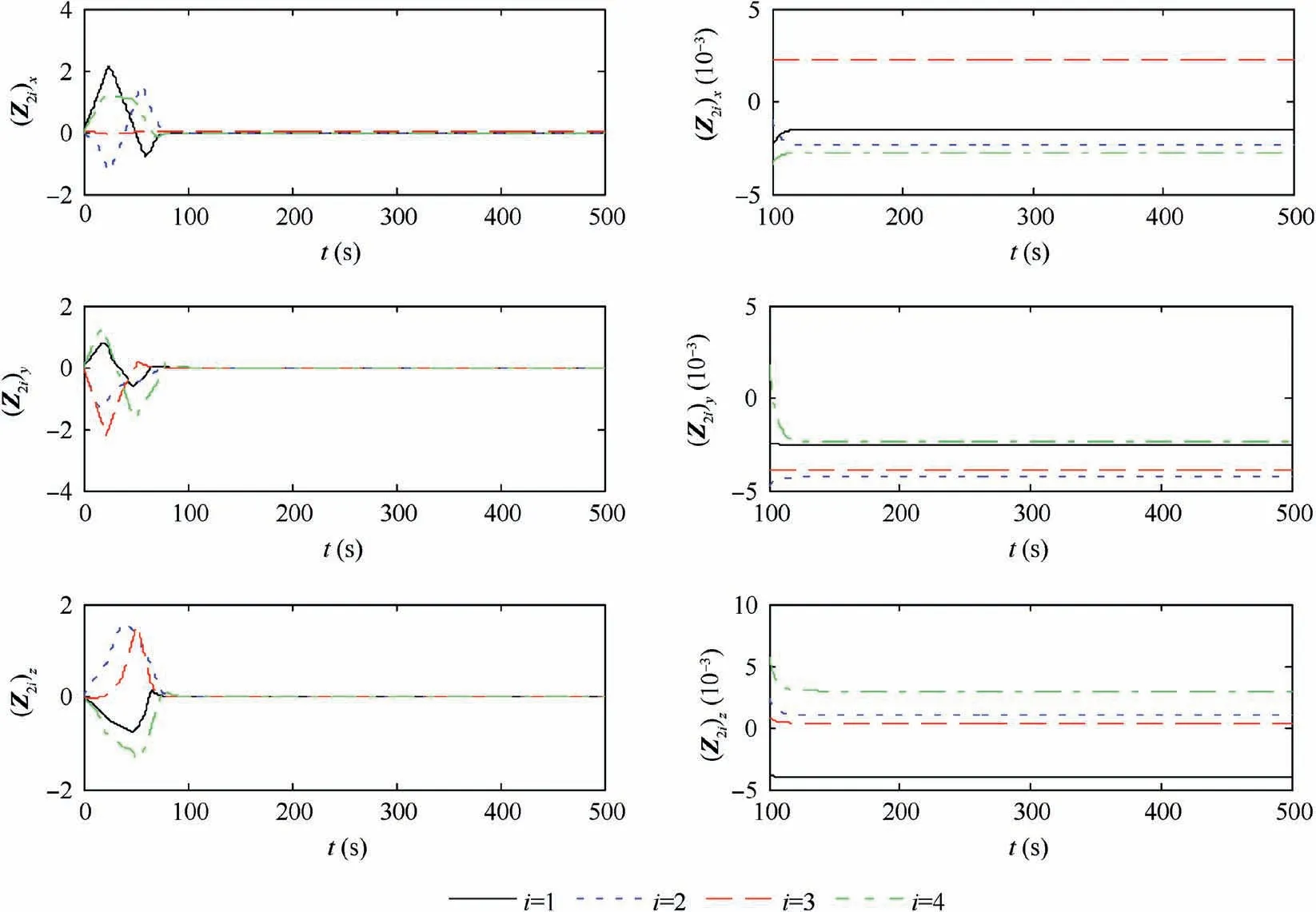
Fig.3 Position error of every follower in SFF under the action of controller Eq.(16).
4.1.Collision avoidance APF
The collision avoidance APF betweenith spacraft andkth spacecraft is defined similarly to Li and Wang34which is given by:

Wherercdenotes the allowable minimum distance andrddenotes the distance at which the APF operates betweenith spacraft andkth spacecraft,respectively.The gradient of the APF is given by

Note that both of the two functions Eq.(27) and Eq.(28)are continuous at ‖ρi-ρk‖=rd.
4.2.Fixed-time TSM surface design considering mutual distance constraints
The TSM surface considering mutal disturbance constraint is designed as the form of

Theorem 3.The TSM surface Eq.(29)keeps the statesx1i converge to origin in fixed time afters1i=0.The bounded settling time is also Ts.And the control input is also nonsingular.
Proof.The lyapunov function is also chosen as the form of Vi,j.The time derivative of Vi,j is calculated as follows:

Similarly analysis to Eq.(10),ei.jconverges to origin within bounded convergent timeTsis hold.The proof process of control input is nonsingular is also similar to Theorem 1.
4.3.Fixed-time observer design
Generally,in system model Eq.(3),the consumption of spacecraft mass Δmi,the external disturbance are not exactly known.These uncertainties,if not handled well,will affect the performance of the controller and even lead to system instability.To better handle them,an observer is designed in this subsection.Before moving on,an assumption is exploited.
Assumption 2.The system uncertainties of spacecraft i contain the assumption of mass and the external disturbance are lumped asdi which is bounded and differentiable and satisfieswhereΛi andΛare known positiveconstants.

Fig.4 Velocity error of every follower in SFF under the action of controller Eq.(16).

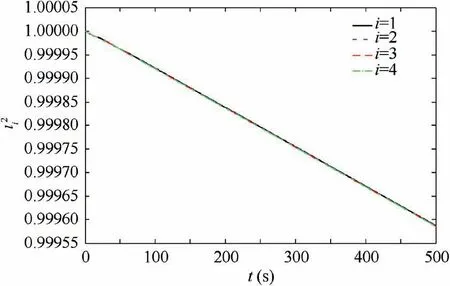
Theorem 4.For the error dynamics Eq.(3),if the observer is designed as the form in Eq.(31)and Assumption2is satisfied,then the termdi/mi will be estimated within fixed-time throughZ2i,and the boundary of time is To.


4.4.Design of coordination controller considering mutual distance constraints

Assumption 3.The initial distance between any two spacecraft in the formation is greater than the safe distance rc.That means that neither of two spacecraft had a collision before control beginning.Also,the distance between the desired positions of any two spacecraft is greater than the safe distance rc.
The controller designed for SFF error dynamics Eq.(3) is stated as:

Theorem 5.For the spacecraft system Eq.(3),the proposed controller Eq.(36)guarantees the following conclusions to be true if Assumptions2and3hold.
(A) The TSM surface Eq.(35) converges to zero with bounded reaching time T2,and the position tracking erroreand velocity error ˙econverge to zero in bounded settling time T3=T2+Ts.
(B) There is no collision between any two spacecraft in SFF during the transition process.
(C) SFF position coordination control is completed under undirected communication topology in fixed-time T3.
(D) All signals are ultimately uniformly bounded.
Proof.The proof process is divided into two steps.The first is the stability of the time t≥To.In this circumstance,Z2i=di/mi.The Lyapunov function is chosen as V2.The time derivative of V2is stated as:

The following analysis is similar to Eq.(24).Finally,one can conclude that the TSM surface Eq.(35) is bounded and converges to zero with bounded reaching timeT2=To+Tr1.Therefore,the stability ofecan be described as follows.

By simply deforming the above equation,the following results can be obtained:

Then according to Eq.(30),ei,jconverges to origin within bounded timeT3=T2+Ts.Consequently,velocity error ˙ei,jalso converges to origin.From the above proof process one obtains thatfi,jis bounded,which implies that there is no collision between any two spacecraft in SFF.Whenei,jand ˙ei,jconverge to origin respectively,the position coordinated control has been completed.
The second step is stability in the duration 0 According to Lemma 2,one infers thatS1is bounded.Then one also infersei,jis bounded and there is no collision between any two spacecraft.Finally,one gets all the signal are ultimately uniformly bounded. Thus,complete the proof. Remark 5.From the proof process of Theorem5,one obtains the boundedness of S1i,j guarantees the boundedness of fi,j.Then one obtains thati is also bounded.However,the expression ofi is too complicated to engineering practice.The controller Eq.(36)is redesigned as where the designed parameterKrepresents the maximum value ofThe new designed coordinated controller also ensures that the conclusions of Theorem 5 are correct. Proof.When t≥To,the Lyapunov function is also chosen as V2.Then the time derivative of V2is The following analysis is similar to Theorem 5,thus it is omitted. Remark 6.The proposed control scheme is free of local minima.According to Eq.(37),There is the unique minima of the Lyapunov function V2only at ei,j=0.V2is continuous anddifferentiable,if and only ifS1=0.After the slingsurface reaches to zero,it has been proved that ei,j converges to origin in fixed-time.Finally,one infers that the proposed control scheme is free of local minima. Remark 7.The combination of TSM surface and APF is inspired by Li et al.36,the main difference between this paper and Li’s is that the design of TSM surface Eq.(29)contains the gradient information of APF.The three directions ofsi are adjusted according to the gradient information of APF rather than a single multiple adjustment based on APF.Also,the control input contains the gradient information of APF which is the key to collision avoidance rather than the time derivative of APF. Remark 8.The parameters of Eq.(41)also need to be set when applying it.The selection of parameters of nonlinear controller is complicated,thus we give the role of every parameter.ϖis used to keep systems stability in the duration0 Remark 9.As mentioned in previous proof process,this approach guarantees the collision avoidance by ensuring that fi,j is bounded.The actual convergent time that the TSM surface Eq.(35)reaches to zero is faster than that of TSM surface Eq.(14)due to the termThe coordinated controller Eq.(41)is also suitable for SFF in an environment with obstacles.There is only a little change infthen it achieves the collision avoidance. Remark 10.The communication topology is used to keep the position synchronization in the trasition process,so the proposed control scheme consumes more energy than that of the form of it omitting the communication topology.The proposed control schemes Eq.(36)and Eq.(41)consume more energy than that of the controller Eq.(16),because the collision avoidance constraint must be satisfied.Although the expressions of the controllers look like complex,they do not affect their real-time performance. In this section the performance of the proposed control schemes is conducted by numerical simulations.A SFF scenario is adopted in which a virtual leader and four followers are involved.In this scenario,the spacecraft are assumed to perform a formation reconfiguration mission,changing from any four positions in space to a rectangular configuration.The orbit parameters of the virtual leader are stated as follows:ar=7178 km,er=0.01,Ωr=0 rad,ir=π/6 rad,ωr=0 rad,θr(0)=0 rad.The mass of the virtual leader ismr=100 kg.It should be noted that the virtual leader is used to generate the desired position,thus the mass of virtual leader can be arbitrary values.The mass of the followers ismi=100 kg.The maximum thrust provided by thrusters of the follower is supposed to be 10 N.External disturbance mainly considers the influence of the earth’s non-spherical perturbation. Fig.5 Control input of every follower in SFF under the action of controller Eq.(16). Fig.6 Time response of parameter Remark 11.The finite-time control theory requires sufficient control force to ensure high control accuracy and finite time stability of the controlled system.This article limits the control input to make the simulation results more realistic.Many articles have made similar restrictions such as Refs.21,24,28,30,36. Fig.7 Time response of CPI1 under the action of controller Eq.(16). Remark 12.The proposed control schemes do not handle the input saturation problem,so the limitation on the amplitude of control input makes the robustness against variation of initial states degraded.But,one can infer from the following simulationresults that the control schemes still work when the amplitude of control force is limited to a proper threshold.For SFF reconfiguration,each spacecraft is located near its desired position,thus the limitation on control force has little impact on the closed loop system stability. The nodeViis used to denote theith spacecraft,and the weighted undirected graph is shown by Fig.1.Then one obtains the weighted adjacency matrixA: Fig.8 Time response of CPI2 under the action of controller Eq.(16). The initial simulation conditions are shown in Table 1.And the values of controller are selected as shown in Table 2.The simulation results are depicted in Figs.2–9.According to previous statements,the bound of reaching time that TSM surface converge to the region φ0is 573.6938 s.The bounded time thatei,jandconverge to Ω1and Ω2respectively is 695.4297 s.According to Fig.2,the actual time thatSi,jconverges to the regionis 240 s.Also according to Figs.3 and 4,the actual time thatei,jandconverge to the regionsrespectively is 350 s,which are far lower than the estimated bound of convergent timeT1.The control input of every follower is shown in Fig.5,which implies that the control scheme still works even though there is a limit on the control input.The time response of parameteris shown in Fig.6,as previous statements,the decreasing ofis used to accelerate the convergence rate of system state.To examine the coordination control effort,two Comprehensive Performance Indexes (CPIs) are introduced13,which are given byThe two indexes CPI1and CPI2are used to evaluate the performance of formation tracking accuracy and formation synchronization accuracy,respectively.Time response of CPI1and CPI2of Eq.(16) are shown in Figs.7 and 8.Form Figs.7 and 8,one can see that the controller Eq.(16) provides faster synchronization accuracy and higher tracking accuracy than its form of ignoring the coordination term.We define the functionto denote the energy cost.The energy consumption of controller Eq.(16) and its form of omitting coordinated term are shown in Fig.9,from which,one can infer that the position synchronization is guaranteed by more energy consumption. Fig.9 Energy consumption comparison between controller Eq.(16) and its form of omitting coordination term. To demonstrate the fixed-time stability of controller Eq.(16),another initial position of every followeras shown in Table 1 is considered.Simulation results show that the actualtime thatSi,jconverges to the regionthe actual time thatei,jandconverge to the regionsrespectively is 340 s,and the position coordination is accomplished after the time instant 340 s.Simulation results also validate the correctness of Theorem 2. Table 1 Initial simulation conditions of controller Eq.(16). Table 2 Main parameters of proposed controllers. Another SFF scenario is conducted to testify the control effort of controller Eq.(41) in which considering mutual distance constraint among spacecraft.The safe distance is set asrc=25 m.Another parameterrdthat the APF starts working is defined asrd=100 m.The initial simulation conditions are shown in Table 3.The system uncertainty is considered as Δmi=-0.2mi*Rand,where Rand denotes a random number between 0 and 1.The values of parameters of controller are shown in Table 2.The simulation results are shown in Fig.10–19.According to previous statements,the bounded time that the observer estimates the uncertainties is 140.4904 s and the bounded reaching time that the TSM surface Eq.(35) converges to origin is 110 s.The actual time according to Fig.10 that the observer has estimated the system uncertainties before 140.5904 s,and the actual time that TSM surface Eq.(35)reaches to zero is about 250 s as Fig.11 shows.The actual settling time thatei,jandconverge to origin is about 280 s,which is far lower than the estimated bounded convergent time 1443.0279 s.And Figs.12 and 13 show the actual control precision ofei,jandandrespectively.Fig.14 shows the controller also works even though there is a limitation on control input.The CPIs are also used to evaluate the performance of formation tracking accuracy and formation synchronization accuracy of controller.Fig.15 shows that the tracking accuracy of controller Eq.(41) is better than its revised form whose the coordination term is omitted in the second half of control process.The tracking accuracy of controller Eq.(41) is better than its revised form is not always hold because Δmiis not identical in the two simulations.Fig.16 shows the better position synchronization performance of Eq.(41).The results depicted in Fig.18 is obtained by omitting APF which means makingm1=0.From Fig.18 one obtains the collision occurs between spacecraft 1 and spacecraft 2.By comparing Fig.17 with Fig.18,one can easily deduce that when applying the proposed controller Eq.(41),the mutual distance constraint is guaranteed.Fig.19 shows the energy consumption of different forms of controller Eq.(41),from which,one infers that the collision avoidance and synchronization need more energy to be guaranteed. Fig.10 Time response of observer. Fig.11 Time response of TSM surface Eq.(35). Fig.12 Position error of every follower in SFF under the action of controller Eq.(41). Fig.13 Velocity error of every follower in SFF under the action of controller Eq.(41). Fig.14 Control input of every follower in SFF under the action of controller Eq.(41). Fig.15 Time response of CPI1 under the action of controller Eq.(41). Fig.16 Time response of CPI2 under the action of controller Eq.(41). Fig.17 Relative distance considering mutual distance constraint under the action of controller Eq.(41). Fig.18 Relative distance without mutual distance constraint under the action of controller Eq.(41). Fig.19 Energy consumption of different conditions under the action of controller Eq.(41). To testify the fixed-time stability,another initial position of each followershown in Table 3 is selected.Simulation results show that the actual time that the sliding surface Eq.(35) converges to zero is about 300 s.The actual time that the tracking errorei,jand velocity errorconverge to the regionrespectively is 350 s.The mutual distance constraint among each spacecraft is also satisfied,the minimum distance is 25.7121 m.Thus,the simulation results also validate the correctness of Theorem 5. Table 3 Initial simulation conditions of controller Eq.(41). The obstacle is assumed at the positionm.The initial position of each spacecraft is assumed asThe other initial conditions are the same to previous statements.The parameters are selected as the same to those in subsection 5.2 exceptK=100,m1=0.02,k1=0.2 and ϖ=0.0005.We also assume that the safe distance between spacecraft and the obstacle isrc=25 m.And the parameterrdis also selected asrd=100 m.The system uncertainty is also considered as Δmi=-0.2mi*Rand.Simulation results are presented in Figs.20–22.The simulation results that without considering the distance constraint are shown in Figs.23–25.Fig.20 shows that the distance constraint of any two spacecraft is satisfied during the transient process.The collisions between spacecraft 2 and 4,and between spacecraft 1 and 4 occur when omitting the distance constraint as shown in Fig.23.From Fig.21,one gets the proposed control scheme keeps the spacecraft avoid colliding the obstacle.The spacecraft 1 collides with the obstacle when omitting the distance constraint as Fig.24 shows.The tracking error of each spacecraft is shown in Fig.21,from which,one obtains that the actual settling time is about 830 s,which is far lower than the calculated boundary 1382.16 s.Comparing Fig.22 with Fig.25,one gets the position synchronization of each spacecraft controlled by Eq.(41) is slower than that controlled by omitting the distance constraint of Eq.(41).Because spacecraft 1 should avoid the obstacle when track its desired trajectory,and spacecraft 1,2,and 4 must make corresponding maneuvers to meet the distance constraint.All of the above simulation results testify the correctness of Theorem 5. Fig.20 Relative distance considering distance constraint in obstacle environment. Fig.21 The distance between each spacecraft and the obstacle considering distance constraint in obstacle environment. Fig.22 Tracking error of each spacecraft considering distance constraint in obstacle environment. Fig.23 Relative distance without considering distance constraint in obstacle environment. Fig.24 The distance between each spacecraft and obstacle without considering distance constraint in obstacle environment. Fig.25 Tracking error of each spacecraft without considering distance constraint in obstacle environment. This paper has addressed the fixed-time stable problem of SFF formation reconfiguration.Two coordinated controllers have been proposed under undirected communication topology.The first controller we proposed associates with a new designed nonsingular TSM surface.To handle the mutual distance constraint among spacecraft,another nonsingular TSM surface has been designed associating with APF.A fixedtime observer was designed to handle system uncertainties.And the second controller was designed based on them.It is theoretically proved that both of two controllers keeps the fixed-time stability of the closed loop system.Finally,simulation results are used to testify the validity of the proposed theorems.Further work will focus on extending the results to the case when actuator saturation and actuator fault.The amplitude of control input in this paper is big,and this problem has not been handled.Further work should focus on dealing with it. Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgements This paper was supported by the Major Program of Natural Science Foundation of China (No.61690210),the Science Fund for Excellent Young Scholars of Heilongjiang Province,China (No.YQ2020F007) and National Natural Science Foundation of China (No.6191101340).


5.Simulation



5.1.The performance of the control scheme Eq.(16)




5.2.The performance of the proposed control scheme Eq.(41)






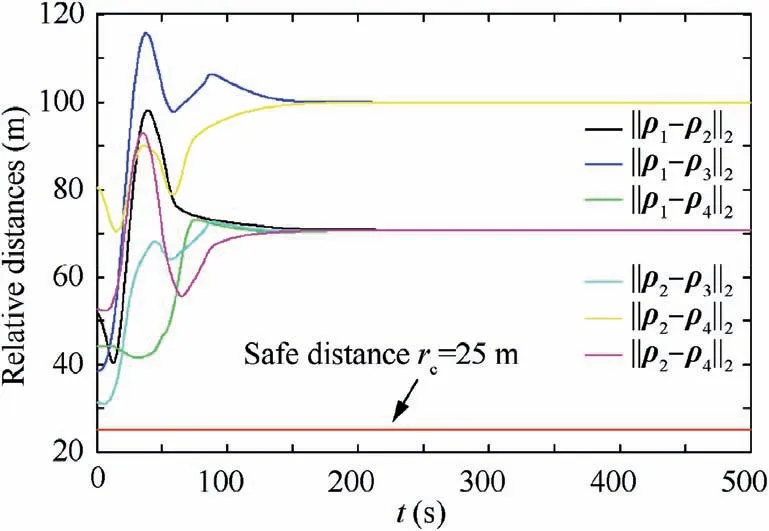



5.3.Another scenario for testing the performance of Eq.(41)








6.Conclusions
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Parameter effects on high-speed UAV ground directional stability using bifurcation analysis
- Supersonic flutter control and optimization of metamaterial plate
- Review of in-space assembly technologies
- Utilisation of turboelectric distribution propulsion in commercial aviation:A review on NASA’s TeDP concept
- The influence of inlet swirl intensity and hot-streak on aerodynamics and thermal characteristics of a high pressure turbine vane
- Full blended blade and endwall design of a compressor cascade
