区域与空间视角下中国城市规模分布与增长

摘 要：检验齐普夫定律和吉布拉定律在中国城市规模分布和增长中的适用性，有利于分析中国城市体系的演变趋势和合理化特征。研究表明：中国城市规模分布基本服从齐普夫定律，但存在明显的分化特征和趋势;中部地区城市规模分布呈现扁平化特征，而其他区域均存在明显的分化特征和趋势，这与其内部城市规模的差异相关;全国和区域层面城市规模增长基本服从吉布拉定律，这与小城市和大城市人口增长较快，而中等城市人口增长较慢相关。因此国家需要调整未来城镇化发展的重点，在中部地区应当注重发展大城市，而其他地区应当注重大中小城市协调发展;另外还需要加大对中等城市的政策倾斜和增强大城市的空间溢出效应，以促进中等城市人口增长。

关键词：人口城镇化;城市规模;齐普夫定律;吉布拉定律

中图分类号：F291.1

文献标识码：A

文章编号：1000-4149（2021）05-0081-14

DOI：10.3969/j.issn.1000-4149.2021.00.041

收稿日期：2021-02-01

;修订日期：2021-06-08

基金项目：国家社会科学基金项目“户籍管制下城市差异化公共服务供给与人口空间集聚优化研究”（18BRK017）;国家社会科学基金项目“城市群战略下中心城市人口集聚的时空演变与空间效应研究”（20BRK019）;中南财经政法大学中央高校基本科研业务费项目“中国城市人口集聚的区域差异与分布动态演进”（2722020JCG011）。

作者简介：杨晓军，经济学博士，中南财经政法大学经济学院副教授。

The Distribution and Growth of Chinas City Size from Regional

and Spatial Perspective

YANG  Xiaojun

（School of Economics， Zhongnan University of Economics and Law，

Wuhan 430073， China）

Abstract：Testing the applicability of Zipfs law and Gibrats law in the distribution and growth of Chinas city size is helpful to analyze the evolution trend and rationalization characteristics of Chinas urban system. The results show that Chinas city size distribution generally obeys Zipfs law， but there are obvious divergence features and trends. The distribution of city size presents a flat feature in the central region， while other regions have obvious divergence features and trends， which are related to their inter-region difference. The growth of city size at the national and regional levels basically obeys Gibrats law， which is related to the rapid population growth of small and big cities， while the slower growth of population in medium-sized cities. Therefore， the focus of future urbanization development needs to be adjusted， and the central region should focus on the development of big cities， while other regions should focus on the coordinated development of big， medium and small cities. It is also necessary to increase policy inclination for medium-sized cities and enhance the spatial spillover effect of big cities to ensure population growth in medium-sized cities.

Keywords：urbanization; city size;Zipfs law;Gibrats law

一、引言

中國城镇化的路径选择存在以大城市为主的集中式和以小城镇为主的分散式两种观点，其争论焦点在于城市体系合理化。一个国家城市体系的合理化有利于高效优化要素资源分配和充分发挥集聚（或扩散）效益优势，这就需要不同规模的城市相互依存、共同发展，既要充分发挥大城市的集聚与辐射效应，又要注重增强中小城市和小城镇的容纳与吸收作用，从而实现大中小城市和小城镇的协调发展。关于合理城市体系的研究既有

基于人口或经济规模等单一指标的分析，也有基于经济、社会、生态等综合指标的分析，本文的讨论主要是基于城市人口规模指标。现有文献主要通过齐普夫（Zipf）定律和吉布拉（Gibrat）定律来检验城市体系是否合理化。因此，利用最新数据来检验齐普夫定律和吉布拉定律在中国城市规模分布和增长中的应用，以揭示城市规模的空间分布动态特征，有助于更好地促进城市规模分布格局的优化与调整，对推动新型城镇化进程和实现城市体系合理化具有重要的现实意义和理论价值。

齐普夫研究表明城市规模分布不仅服从帕累托分布，而且帕累托指数为1[1]，这就是所谓的“齐普夫定律”或“位序—规模法则”，它通常作为一种检验城市体系合理的标准，以此来判断城市规模分布是否合理化。

吉布拉认为城市规模的增长率与其初始规模无关，即不同规模城市的人口增长率没有显著差别，都保持在自然增长率水平，这被学者们称之为“吉布拉定律”[2]。

随后国外学者们运用不同国家或地区的实证数据来验证其有效性，研究结果存在差异：一是认为城市规模分布遵循齐普夫定律[3-5];二是认为城市规模服从帕累托分布，但帕累托指数大于或小于1[6-9];三是认为城市规模上尾部分的分布遵循齐普夫定律[10-11];四是认为城市规模分布服从对数正态分布，且城市规模与其增长率无关，满足吉布拉定律[12-15];五是认为城市规模分布服从双帕累托对数正态分布[16]。中国正处于城镇化快速发展阶段，其城市规模分布和增长也随之不断变化和调整，国内外学者运用上述方法对中国城市人口规模分布和增长进行了验证。有的学者认为其服从帕累托分布，存在明显的区域特征[17]，且基本服从齐普夫定律[18]，人口在不同规模城市间的分布逐渐趋于合理[19];但也有学者认为其并不服从齐普夫定律[20-21]，而是呈现出典型的扁平化特征，表现为大城市和小城市、小城镇相对较少，中等城市分布密度较高，特大型城市相对合理[22]，这也与小城市高速增长及中等规模城市增长相对停滞密切相关[23];还有学者认为其符合双帕累托对数正态分布，且拥有对数正态分布的中间主体，上下尾部更接近幂律分布，这与处于上尾的大中城市数量和人口规模增长迅速，处于下尾的中小城市数量多但人口规模增长动力相对不足有关[24]，且总体上不满足吉布拉定律，这与城镇化发展阶段密切相关[25]。

上述研究为本文提供了很好的经验借鉴，但也存在进一步探讨的问题，如现有文献所使用的数据多为不同时点的截面数据，且衡量城市规模指标存在争议;时间范围上主要在2010年以前，需要更新数据分析其最新特征;研究范圍主要是全国总体为主，较少涉及区域层面;未考虑城市规模分布与增长的空间依赖性。因此，本文根据2006—2017年中国县级及以上城市面板数据，构建衡量城市规模的指标，基于全国、区域和空间视角检验齐普夫定律和吉布拉定律在中国城市规模分布和增长中的适用性，分析中国城市体系的演变特征和合理化趋势，并据此提出相应的政策建议。

二、数据与典型化事实

1. 数据

现有研究中衡量城市规模的指标主要有两类：一是来自美国国防气象卫星计划/线性扫描系统（DMSP/OLS）的夜间灯光数据[23，26-29]，它是一个较好的替代衡量指标，但不能精确衡量城市人口数;二是基于人口统计数据指标，包括《中国城市统计年鉴》中的市辖区户籍人口指标[17，30]、《中国城市建设统计年鉴》中的城区常住人口指标[19]、全国人口普查数据中的城镇常住人口指标[22，25，31-32]和联合国人口司编撰的《世界城市化展望》中的市域城镇人口指标[24，33]。上述指标涉及城镇、市辖区和城区三个范围，具体来看，城镇包括设市建制的城市市区和建制镇的镇区，市辖区包括城区和郊区人口，而城区主要是城市市政设施建设和经济发展的核心区，因而相对于城镇和市辖区而言，城区能够更准确地反映城市的范围。此外，2014年国务院印发的《关于调整城市规模划分标准的通知》中也将城区常住人口作为衡量城市规模的依据。基于此，本文采用城区常住人口指标衡量城市规模。

由于《中国城市建设统计年鉴》中准确衡量城区常住人口数据起始于2006年，因此本文将时间范围限定在2006—2017年。在样本数据期，由于撤县设区和新设县级市等行政区划调整引起城市数量发生变化，为保持每个年度城市数量一致以便于比较分析，本文将考察期内27个撤县设区的县级市在撤销前的人口数据并入相应的地级市，并删除32个新设县级市，最终数据处理后共获得628个城市数据。关于城市规模的划分标准，根据2014年11月国务院印发的《关于调整城市规模划分标准的通知》（国发〔2014〕51号），以城区常住人口为统计口径，其中城区常住人口50万以下的城市为小城市，城区常住人口50万以上100万以下的城市为中等城市，城区常住人口100万以上500万以下的城市为大城市，城区常住人口500万以上1000万以下的城市为特大城市，城区常住人口1000万以上的城市为超大城市。

2. 典型化事实

中国城市规模具有明显的空间非均衡性态势，这已经成为城镇化进程中的客观存在。因此需要考察区域层面城市规模的差异性。关于区域划分标准，本文依据国家统计局2011年6月公布的《东西中部和东北地区划分方法》，将我国的经济区域划分为东部、中部、西部和东北部四大地区，其中东部地区包括北京、天津、河北、上海、江苏、浙江、福建、山东、广东和海南10个省和直辖市;中部地区包括山西、安徽、江西、河南、湖北和湖南6个省;西部地区包括内蒙古、广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、宁夏、青海和新疆12个省、自治区和直辖市;东北地区包括辽宁、吉林、黑龙江3个省。最终样本中，东部、中部、西部和东北地区分别选择210、167、165和86个城市。

为了揭示考察期内城市规模的演变趋势，本文对全国及各区域城市人口规模进行均值处理，具体如图1所示。从演变趋势来看，考察期内全国及各区域城市人口平均规模均呈现出明显的上升趋势。在增长数量方面，东部城市人口平均规模的增长数量最高，年均增长量为2.69万人;其次是西部城市，年均增长量为1.95万人;再次是中部城市，年均增长量为1.57万人;最后是东北部城市，年均增长量仅为0.51万人。在增长速度方面，西部城市人口平均规模的增长速度最快，年均增长率为3.81%;其次是中部城市，年均增长率为3.08%;再次是东部城市，年均增长率为2.86%;最后是东北部城市，年均增长率仅为0.96%。在差异程度方面，考察期内区域间城市人口平均规模的绝对差异明显，极差呈现出不断扩大的趋势，从2006年的39.24万人扩大到2017年的54.83万人。具体来看，东部城市人口平均规模一直处于最高水平，平均值为94.51万人，远高于全国城市平均水平;其他三个区域的城市平均人口规模均低于全国平均水平，且差异不明显。

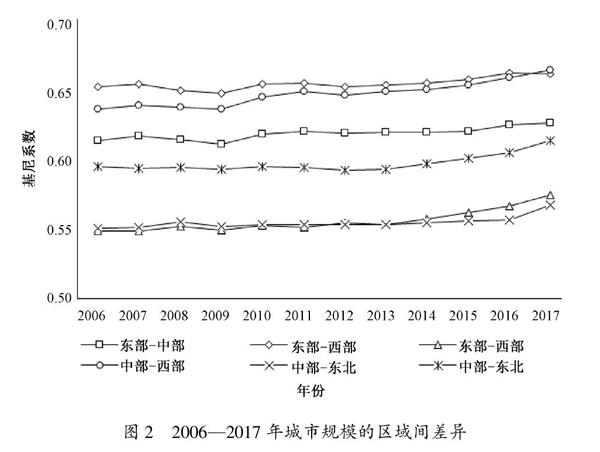
为了详细反映中国城市规模的区域间差异，本文利用达古姆（Dagum）基尼系数[34]进行测算，结果如图2所示。总体来看，四大区域间城市规模存在较大差异且呈现扩大化趋势。从数值来看，东部与西部、中部与西部的区域间城市人口规模差异最大，其基尼系数的均值分别为0.67和0.65;东部与中部、西部与东北的区域间差异较大，其基尼系数的均值分别为0.62和0.60;东部和东北、中部和东北的区域间差异较小，其基尼系数的均值分别为0.56和0.56。从演变趋势来看，各区域间城市人口规模差异总体上呈现小幅上升趋势，但其增长速度存在差异，如东部与东北区域间差异的增长速度最快，其基尼系数的年均增长率为0.42%，而东部与西部区域间差异的增长速度最慢，其基尼系数的年均增长率仅为0.13%。由此可见，中国城市规模存在较高的区域间差异，因此区域层面分析有助于更好地了解其特征。

三、城市规模分布：齐普夫定律检验

1. 经验估计

大量文献采用帕累托指数研究城市规模分布状况，具体公式为：

R=A·P-a（1）

其中，R为城市位序，即一个城市的规模在全国或区域内的排列次序，P为城市规模，a为描述城市规模分布形状的参数（即帕累托指数），且a>0，A为参数。现有实证研究通常估计帕累托指数是否为1以及其随时间变化的趋势。如果a等于1，说明城市规模分布满足齐普夫定律，即中国城市体系比较合理;而a不等于1则意味着城市规模分布不满足齐普夫定律。如果a值越大，说明城市规模越均匀，反之城市规模越集中;a值逐渐增加，说明城市规模分布呈现扁平化趋势，反之城市规模分布呈现分化趋势。

本文利用极大似然估计对样本数据是否符合帕累托分布进行检验，由于篇幅受限，其结果备索。结果表明不同样本城市规模分布均在1%的显著性水平上通过了帕累托检验，说明中国城市规模分布服从帕累托分布。因此建立实证模型来估计帕累托指数：

lnR=c-alnP+ε（2）

其中，c为常数，ε为误差项。

加贝克斯（Gabaix）和伊布拉吉莫夫（Ibragimov）研究表明，式（2）的OLS回归结果可能存在偏差，需要对模型中的城市位序进行修正[35]，具体模型如下：

ln（R-1/2）=c-alnP+ε（3）

表1报告了中国城市规模分布的Gabaix-Ibragimov回归结果。结果表明，总体样本中，帕累托指数位于0.951—0.991之间且通过1%的显著性水平，说明中国城市规模总体分布近似满足齐普夫定律，中国的城市体系比较合理。随着城市样本选取量的增加，帕累托指数逐渐减少，即随着中小城市数量增加，中国城市规模分布呈现分化趋势，人口向大城市集聚的现象尤为突出;随着时间推移，各城市样本的帕累托指数也呈现出减少趋势，尤其是2011年以后各城市样本的下降趋势非常明显

，说明中国城市体系从2011年开始出现不合理的态势，这与城市化进程中重点发展大城市，忽视中小城市发展密切相关。此外，我们注意到截点城市的选择与齐普夫定律是否成立存在极大关系，因此通过编撰计算程序测算出帕累托指数最接近1时所对应的城市数量，即最优截点城市数量。结果显示，最优截点城市数量其范围在611—626之间，非常接近本文选取的城市样本量，这也进一步说明齐普夫定律在中国城市规模分布中有较好的适用性和合理性。

下面进一步检验区域层面城市规模分布是否与全国样本存在显著差异。表2报告了区域层面城市规模分布的Gabaix-Ibragimov回归结果。结果表明，各区域城市规模总体分布也近似满足齐普夫定律，但也存在差异性。其中，中部地区的帕累托指数大于1而其他地区均小于1，说明中部地区城市规模分布存在扁平化特征，而其他地区存在分化特征。随着时间推移，各区域城市样本的帕累托指数均呈现下降趋势，即城市规模分布的分化趋势逐渐明显。综合来看，中部地区城市规模分布比较均匀，而其他地区存在明显的集聚现象。

2. 空間距离约束

由于人口在城市间可以自由流动，一个城市与邻近城市的人口之间存在密切联系，即城市规模分布存在空间依赖性 [36]。因此，本文通过基于距离的城市地理样本选择，引入空间变量分析城市规模分布随地理距离变化的规律。第一步是确定邻近城市的地理样本，根据空间地理距离考虑半径500公里范围内城市的所有可能性组合，其中城市间地理距离数据来源于国家基础地理信息系统1∶400万中国地形数据库，并利用ArcGIS软件进行测算。以一个城市为中心，从城市间最短距离10公里开始，选择每增加10公里的城市样本，最终形成了49个距离样本和20904个城市样本数据。

在这些样本数据中，所有规模的城市均被考虑在内。由于在不同城市的相同距离样本中会包括完全相同的城市，在此删除重复值。第二步是利用极大似然估计对每个距离样本数据进行帕累托分布检验，结果表明2006—2017年49个距离样本数据均服从帕累托分布。第三步是采用Gabaix-Ibragimov回归模型估计每个距离样本城市规模分布的帕累托指数，最终每年可以获得49个不同的估计值。第四步是使用局部多项式平滑对地理距离和估计的帕累托指数之间的关系进行非参数估计。本文仅列示了部分年份的非参数估计结果，如图3所示，图中虚线部分为95%的置信区间。结果表明，随着地理距离增加，帕累托指数总体呈现下降趋势，且在100公里范围内的下降趋势非常明显，在100—500公里范围内，帕累托指数呈现出波动趋势，且近似等于1。从时间趋势来看，在不同地理距离上，2006年帕累托指数主要大于1，而2017年却小于1，这说明随着时间推移，城市规模分布的分化趋势逐渐明显，这与上述分析相一致。综合来看，考虑到空间因素后，中国城市规模分布也近似满足齐普夫定律，且分化趋势日趋明显。

四、城市规模增长：吉布拉定律检验

1. 线性模型估计

吉布拉定律主要用来考察城市规模增长率与初始规模的关系，本文建立如下回归模型：

gi=α+βlnPi+εi（4）

其中，g为城市规模的标准化增长率，即增长率减均值再除以标准差;α为常数，β为回归系数;i为某个城市，ε为误差项。如果β为零或者不显著，则表明城市增长率与其初始规模无关，即城市规模增长满足吉布拉定律，反之则表明吉布拉定律假设不成立，即城市规模体系没有达到最优状态。

考虑到城市规模增长率与间隔时间密切相关，本文对其取值范围限定在1—11年，以尽可能了解城市规模增长率的准确变化趋势，进而增强模型检验的有效性。表3报告了中国城市初始规模对不同时间间隔增长率的回归结果。从结果可以看出，城市初始规模对增长率的影响存在较大差异。具体来看，2006年城市规模与其2—8年增长率，2007年城市规模与其1—7年增长率，2008年城市规模与其1—5年增长率均呈现显著的负相关，这说明初始规模较大的城市往往具有较低的增长率，即表明吉布拉定律假设不成立。2009年和2010年城市规模对不同增长率的影响均不显著，则表明吉布拉定律假设成立。从2011年开始，城市规模对增长率的影响开始呈现显著正相关，说明吉布拉定律假设不成立。综上所述，从年份来看，2009—2010年中国城市规模增长满足吉布拉定律;从时间跨度来看，9年及以上城市规模增长满足吉布拉定律，这说明短期内城市规模增长可能不服从吉布拉定律，但从长期来看却服从吉布拉定律。

下面进一步分析区域层面城市初始规模对增长率的影响。表4报告了区域层面城市初始规模（2006年）对不同时间间隔增长率的回归结果，其他年份城市的回归结果备索。结果表明，东部、中部和西部地区少数年份的城市初始规模与增长率呈现显著负相关或正相关，且这些增长率的时间间隔均在5年及以下，5年以上城市规模增长率与初始规模均不存在显著性相关，这说明虽然短期内存在城市初始规模与增长率相关的事实，但是长期内城市规模增长与初始规模不存在相关性;东北地区城市初始规模与增长率均不存在显著性相关。综合来看，区域层面城市规模增长基本服从吉布拉定律。

2. 非线性模型估计

本文参考现有研究的做法[11-12，37]

建立非参数估计模型。

gi=m（pi）+εi（5）

其中，p为城市规模的自然对数，即p=lnP;m（pi）为利用pi估计所有p的回归曲线，其估计值为m^（p），是围绕p点的局部平均值，并使用对称、加权和连续的核密度（如围绕p对称的连续加权函数）围绕p进行平滑处理。基于哈德尔（Hrdle）提出的纳达拉亚-沃森（Nadaraya-Watson）估计方法[38]，计算其条件均值：

m^（p）=n-1∑ni=1Kh（p-pi）gin-1∑ni=1Kh（p-pi）（6）

其中，K为核函数，本文采用埃帕内奇尼科夫（Epanechnikov）核函数[39];h为带宽。

基于全国和区域层面城市规模与增长率的数据，采用500个样本的自主法（bootstrap）和95%的置信区间进行非参数局部线性核回归，其结果与表3和表4线性估计结果基本一致。由于篇幅受限，本文不再列出相应的回归估计值，其结果备索。下面主要利用模型给出的城市增长率条件均值来分析其与城市初始规模的非线性关系，本文仅列出部分年份的非线性估计结果，如图4所示，图中虚线部分为95%的置信区间，该置信区间非常小，几乎和模型曲线重合，但在图4 2006—2017年图中可以看出一点。

结果表明，2006—2010年城市规模增长率与2006年城市规模呈现“U”型关系，即随着城市规模增加，增长率呈现出先下降后上升趋势;30万—1000万人口城市的增长率为负值，且最小值在400万人口城市左右。这说明对小城市而言，规模越小越有利于人口增长;中等城市和大城市规模越大越不利于人口增长;特大城市规模与其增长率虽呈现负相关，但却呈现出逐渐减少的趋势;超大城市规模与增长率呈现正相关，这与其人口集聚优势密切相关。2010—2014年城市規模增长率与2010年城市规模呈现负相关，且40万人口以上城市的人口增长率均为负值，但其人口增长率的下降幅度较小。这说明该期间内中等及以上规模城市的人口增长率呈现出微弱的下降趋势。2014—2017年城市规模增长率与2014年城市规模呈现先上升后下降的倒“U”型态势。具体来说，小城市规模增长率基本为零，中等城市和大城市的增长率与其规模呈现显著正相关，而特大城市和超大城市具有显著负相关，且超大城市具有负的人口增长率。这说明该时期内中等城市和大城市具有较高的人口增长率。从总体时间样本2006—2017年来看，城市规模增长率与其初始规模呈现倒“N”型态势，且10万以下和200万—1000万人口的城市增长率为正值，40万—200万人口的城市增长率为负值。这说明考察期内小城市、大城市和特大城市具有较高的人口增长率，而中等城市和规模较小的大城市陷入人口增长停滞期。综合来看，城市规模增长率与其初始规模并不存在明显相关性，即服从吉布拉定律，这与上述分析基本一致。

3. 空间模型估计

如果城市规模存在不同程度的空间依赖性，采用上述估计方法也可能会存在偏误。本文采用全局莫兰指数考察城市规模及其增长率是否存在空间相关性，其中空间权重矩阵的元素取值为城市间地理距离的倒数。通常采用标准化统计量Z值来检验莫兰指数的显著性水平。结果表明：城市规模的莫兰指数值在0.035—0.049之间且在统计上满足1%的显著性水平，这表明城市人口规模存在明显的空间正相关，但空间关联性不强;除城市规模间隔1年或2年增长率在个别年份不存在空间相关性外，其余城市规模增长率的莫兰指数值在0.024—0.142之间且在统计上显著，这表明城市增长率也存在一定的空间相关性。从时间维度来看，城市规模及其增长率的莫兰指数值均呈现出上升趋势，这充分说明城市规模的空间依赖性呈现增强态势。基于此，本文构建空间计量模型如下：

gi=α+βpi+ρwijgi+εi（7）

其中，ρ代表空間回归系数，w代表空间权重矩阵。

基于全国和区域层面城市规模与增长率的数据，采用空间计量模型考察城市初始规模对增长率的影响，其结果与线性回归估计结果基本一致。由于篇幅受限，本文不再列出相应的回归估计值，其结果备索。

上述分析均是基于截面数据的分析结果，而城市规模增长是一个连续过程，需要利用面板数据进一步考察。因此，本文构建衡量城市初始规模对其增长率影响的空间面板计量模型：

gi，t=βpi，t+ρ∑nj=1wijgi，t+θ∑nj=1wijpi，t+μi+ηt+εi，t，εi，t=λ∑nj=1wijεi，t+σi，t（8）

其中，λ代表空间误差系数，θ代表基期城市规模的空间影响，μ代表个体效应，η代表时间效应。现有常用空间计量模型主要包括空间滞后模型（SAR）、空间误差模型（SEM）和空间杜宾模型（SDM）三种形式，本文使用LR检验确定SAR模型、SEM模型或SDM模型类型，使用豪斯曼（Hausman）检验判断固定效应或随机效应。

表5报告了中国城市初始规模对不同时间间隔增长率的面板回归结果。模型选择中，LR检验结果表明所有模型均应选择SDM模型;豪斯曼检验结果表明所有模型均应使用固定效应模型。回归结果表明，除10年增长率模型外，各模型中空间回归系数ρ均大于零且在统计上显著，说明全国城市规模存在显著为正的空间相关性，同时城市规模的空间项θ为正值且在统计上满足1%的显著性水平，说明周边城市规模增加对本地城市规模增长速度具有显著的促进作用，即空间外溢是促进城市规模快速增长的一个重要因素。所有模型中城市规模的回归系数β均小于零且在统计上显著，说明中国城市人口规模的增长率与初始规模呈现负相关，即城市规模较小的城市拥有较大的增长率，而城市规模较大的城市拥有较小的增长率。从时间趋势来看，城市初始规模对其增长率的影响会随着时间推移呈现出先上升后下降的趋势，且对4年增长率的影响最大。综合来看，中国城市规模存在显著为正的空间相关性和空间外溢性，且与其增长率呈现显著负相关。

五、结论与建议

本文基于2006—2017年中国628个城市规模数据，采用齐普夫定律和吉布拉定律分别检验城市规模分布和增长状况，得出如下研究结论：中国城市规模分布基本服从齐普夫定律，这表明中国城市体系合理性较高;但存在明显的分化特征和趋势;中部地区城市规模分布呈现扁平化特征，而其他区域均存在明显的分化特征和趋势，这与中部地区城市规模差异较小有关;全国和区域层面城市规模增长基本服从吉布拉定律，这与小城市和大城市人口增长较快，而中等城市人口增长较慢相关;考虑到空间因素后，中国城市规模增长率与其初始规模呈现显著负相关。

基于上述研究结论，得出如下政策建议：第一，科学认识城市规模的分布规律。中国城市规模体系比较合理，针对其日益明显的分化趋势，需要调整未来城镇化战略发展的重点，不仅要一如既往地重视大城市（尤其是特大和超大城市）发展，也应该重新重视中小城市发展，最终实现大中小城市协调发展。在现有资源配置不均衡情况下，人口向大城市集聚是用脚投票的结果，这就要求政府部门在制定政策时应该在充分考虑其资源禀赋和区位优势的基础上，明确其在国家和地区发展中的角色及定位功能，制定差异化措施保障实现城市发展，如中部地区应该注重大城市发展，通过加快承接东部地区制造业转移等不断增加大城市人口规模，以改变其城市体系扁平化特征;而其他地区要注重控制大城市规模，注重大中小城市协调发展。第二，充分重视城市人口规模的增长态势。由于中等城市人口规模增长缓慢是导致中国城市体系不够均衡的重要原因，这就要求政府在制定城市人口规模协调发展政策时一方面要加大对中等城市的政策倾斜，通过采取某些制度性措施保障中等城市实现人口快速增长，这不能仅仅依靠城市自身的经济发展水平和质量的提升，也要注重吸引人口的优惠政策出台或高质量的市政公用设施水平，以全面促进这些城市经济健康发展;另一方面也要注重大城市的空间溢出效应，增强大城市的空间溢出能力，这既可以一定程度上缓解某些城市由于人口过度集聚所产生的城市病问题，又可以强化其对周围城市的辐射力，实现区域人口协同发展和构建合理化城市体系。

参考文献：

[1]ZIPF G K. Human behavior and the principle of least effort[M]. Cambridge， MA： Addison-Wesley， 1949：364-376.

[2]GONZLEZ-VAL R， LANASPA L， SANZ-GRACIA F. Gibrats law for cities， growth regressions and sample size [J]. Economics Letters， 2013，18（2）： 367-369.

[3]KRUGMAN P. Confronting the mystery of urban hierarchy[J]. Journal of the Japanese and International Economics， 1996， 10（23）： 399-418.

[4]ROZENFELD H D， RYBSKI D， GABAIX X， MAKSE H A. The area and population of cities： new insights from a different perspective on cities[J]. American Economic Review， 2011， 101（5）： 2205-2225.

[5]BERRY B J L， OKULICZ-KOZARYN A. The city size distribution debate： resolution for US urban regions and megalopolitan areas[J]. Cities， 2012， 29（1）： 17-23.

[6]ROSEN K T， RESNICK M. The size distribution of cities： an examination of the Pareto law and primacy[J]. Journal of Urban Economics， 1980， 8（2）： 165-186.

[7]BLACK D， HENDERSON J V. Urban evolution in the USA[J]. Journal of Economic Geography， 2003， 3（4）： 343-372.

[8]NITSCH V. Zipf zipped[J]. Journal of Urban Economics， 2005， 57（1）： 86-100.

[9]SOO K T. Zipfs law for cities： a cross-country investigation[J]. Regional Science and Urban Economics， 2005， 35（3）： 239-263.

[10]GABAIX X. Zipfs law for cities： an explanation[J]. Quarterly Journal of Economics， 1999， 114（3）：739-767.

[11]IOANNIDES Y， OVERMAN H. Zipfs law for cities： an empirical examination[J]. Regional Science and Urban Economics， 2003， 33（2）： 127-137.

[12]EECKHOUT J. Gibrats law for （all） cities[J]. American Economic Review， 2004， 94（5）： 1429-1451.

[13]LEVY M. Gibrats law for （all） cities： comment[J]. American Economic Review， 2009， 99（4）： 1672-1675.

[14]IOANNIDES Y， SKOURAS S. US city size distribution： robustly Pareto， but only in the tail[J]. Journal of Urban Economics， 2013， 73（1）： 18-29.

[15]GONZLEZ-VAL R， LANASPA L， SANZ-GRACIA F. New evidence on Gibrats law for cities[J]. Urban Studies， 2014， 51（1）： 93-115.

[16]GIESEN K， ZIMMERMANN A， SUEDEKUM J. The size distribution across all cities： double Pareto lognormal strikes[J]. Journal of Urban Economics， 2010， 68（2）： 129-137.

[17]高鸿鹰，武康平. 我国城市规模分布Pareto指数测算及影响因素分析[J]. 数量经济技术经济研究，2007（4）：43-52.

[18]GANGOPADHYAY K， BASU B. City size distributions for India and China[J]. Physica A： Statistical Mechanics and Its Applications， 2009， 388（13）： 2682-2688.

[19]张车伟，蔡翼飞. 中国城镇化格局变动与人口合理分布[J]. 中国人口科学，2012（6）：44-57.

[20]ANDERSON G， GE Y. The size distribution of Chinese cities[J]. Regional Science and Urban Economics， 2005， 35（6）： 756-776.

[21]LUCKSTEAD J， DEVADOSS S. A comparison of city size distributions for China and India from 1950 to 2010[J]. Economics Letters， 2014， 124（2）： 290-295.

[22]梁琦，陈强远，王如玉. 户籍改革、劳动力流动与城市层级体系优化[J]. 中国社会科学， 2013（12）：36-59.

[23]李松林，刘修岩. 中国城市体系规模分布扁平化：多维区域验证与经济解释[J]. 世界经济，2017（11）：146-171.

[24]邓智团，樊豪斌. 中国城市人口规模分布規律研究[J]. 中国人口科学，2016（4）：48-60.

[25]魏守华，孙宁，姜悦. Zipf定律与Gibrat定律在中国城市规模分布中的适用性[J]. 世界经济，2018（9）：98-122.

[26]ZENG C， ZHOU Y， WANG S， et al. Population spatialization in China based on night-time imagery and land use data[J]. International Journal of Remote Sensing， 2011， 32（24）： 9599-9620.

[27]吴健生，刘浩，彭建，马琳. 中国城市体系等级结构及其空间格局——基于DMSP/OLS夜间灯光数据的实证[J]. 地理学报，2014（6）：759-770.

[28]HUANG Q X， HE C Y， GAO B， et al. Detecting the 20 year city-size dynamics in China with a rank clock approach and DMSP/OLS nighttime data[J]. Landscape and Urban Planning， 2015， 137（1）： 138-148.

[29]JIANG B， YIN J， LIU Q. Zipfs law for all the natural cities around the world[J]. International Journal of Geographical Information Science， 2015， 29（3）： 498-522.

[30]魏守華，周山人，千慧雄. 中国城市规模偏差研究[J]. 中国工业经济，2015（4）：5-17.

[31]陆铭，高虹，佐藤宏. 城市规模与包容性就业[J]. 中国社会科学，2012（10）：47-66.

[32]唐为. 中国城市规模分布体系过于扁平化吗？ [J]. 世界经济文汇，2016（1）：36-51.

[33]孙斌栋，金晓溪，林杰. 走向大中小城市协调发展的中国新型城镇化格局——1952年以来中国城市规模分布演化与影响因素[J]. 地理研究，2019（1）：75-84.

[34]DAGUM C. A new approach to the decomposition of the Gini income inequality ratio[J]. Empirical Economics， 1997， 22（4）： 515-531.

[35]GABAIX X， IBRAGIMOV R. Rank-1/2： a simple way to improve the OLS estimation of tail exponents[J]. Journal of Business and Economic Statistics， 2011， 29（1）： 24-39.

[36]GONZLEZ-VAL R. US city size distribution and space[J]. Spatial Economic Analysis， 2019， 14（3）： 283-300.

[37]GONZLEZ-VAL R. The evolution of U.S. city size distribution from a long-term perspective （1900-2000） [J]. Journal of Regional Science， 2010， 50（5）： 952-972.

[38]HRDLE W. Applied nonparametric regression[M]. Cambridge， New York and Melbourne： Cambridge University Press， 1990： 32-33.

[39]EPANECHNIKOV V A. Nonparametric estimations of a multivariate probability density [J]. Theory of Probability & Its Applications， 1969，14（1）： 153-158.

[责任编辑 武 玉]