基于S域变换的声压衰减曲线计算方法优化

桂 桂，高 旭，孙 磊，鄂治群，尹永钊，付志勇

(1.中国测试技术研究院，四川 成都 610021;2.中国人民解放军32603 部队，四川 成都 610000)

0 引 言

混响时间是声学工程评价中最为常用的参数之一，在现行标准中，定义为声音已达到稳态后停止声源，平均声能密度自原始值衰变百万分之一（60 dB）所需要的时间[1]。在音乐厅、体育馆、会议室等对室内声学指标要求较高的场合的声学评价中，由于混响时间最为直观，易于感受，因此常常被采用为中期质量控制和工程验收的主要测试项目。故而混响时间测量的准确与否一方面关系到建筑声学评价的可靠性，另一方面关系到与之相关的建筑材料、机械设备等声学测量的准确性。

现有混响时间测量方法主要分为脉冲响应法和中断声源法[2]。脉冲响应法是指通过把房间内某一点发出的狄拉克函数脉冲声在另一点形成的声压平方进行反向积分来获取衰减曲线的方法；中断声源法与之类似，是采用窄带噪声或粉红噪声激励房间，然后直接记录声压级的衰减来获取衰减曲线。可以看到，不管采用何种方法，混响时间最终都要依靠声压衰减曲线来计算得到，因此，声压衰减曲线的准确度直接影响到了混响时间测量的准确性[3]。

随着仪器技术的发展，现有声学测量仪器种类繁多，但在实际应用中，声能密度的衰减速率仍然需要依靠声级计、噪声频谱分析仪等设备测量得到。其结果不可避免的受到了仪器设备自身性能的影响，设置不同仪器参数，会给测量结果带来不同程度的误差，其中最为明显的是时间计权函数中时间常数τ 的选择。蔡德威等研究了一种基于DSP 的时间计权声级算法[4]；张明铎等分析了积分声级计的时间计权特性对等效连续A 声级（LAeq）的影响[5]；莫方朔等提出了估值混响时间的声级残差最小二乘非线性拟合法[6]。本文在分析时间计权声级计算原理的基础上，提出了一种基于拉普拉斯变换的减小时间计权参数误差的方法，经实验验证，该方法能够广泛应用于吸声系数测量领域。

1 时间计权对混响时间测量结果的影响

由于动态测试中信号随时间变换较快，实际测试时为取得有效值，现有声级计、噪声统计分析仪等设备均采用时间计权的方法保证数据准确可靠。目前，丹麦B&K 公司提供了国际最高标准的声级计产品，本文以如图1 所示B&K 3160 型信号分析仪为例，探讨时间计权对混响时间测量结果的影响。

时间计权通常定义为规定时间常数的时间指数函数，该函数对声压信号的平方进行计权。时间计权声级为经时间计权的频率计权声压信号平方在运行时间内的时间平均与基准值平方之比，取以10为底的对数乘以10[7]。对信号求时间计权的过程实际上是使用单实极点为 −1/τ（指数时间计权）的低通滤波器对信号进行滤波。在某观察时刻t的A计权和时间计权声级用公式（1）表示[8]：

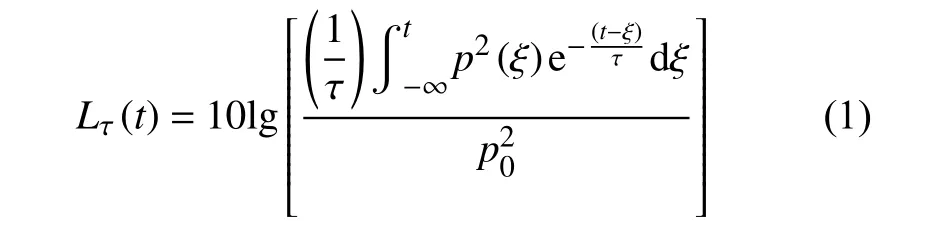
式中：τ——时间计权的指数时间常数，s；

ξ——从过去的某时刻，到观测时刻t的时间积分的虚拟变量；

p(ξ)——瞬时声压信号；

p0——基准值，20 µPa。

可以看出，采用不同的指数时间常数值，对最终实测的声压级结果影响很大。在现行的混响时间测试方法中，最终混响时间结果是由声压衰减曲线计算而来。因此，时间常数的选择直接影响到了混响时间的测量。针对同一正弦信号，当τ 分别为1/8 s、1/4 s、1/2 s、1 s 时测得的声压级结果如图2 所示。

图2 不同时间常数下声压级测量结果

可以看到，不同时间常数下声压衰减速度明显不同，在计算混响时间时，叠加误差将会导致测试结果相差甚远，最终影响到测试精度。以图中所用时间计权函数为例，四条曲线的斜率即代表了最终声压级的衰减速度，计算其斜率结果如表1 所示。

从表1 结果可以看到，不同档位（不同时间计权函数）对最终结果影响很大，通常所用设备一般包含F 档（τF=1/8 s）和S 档（τs=1 s），其声压衰减速度相差30.6 dB/s。事实上，表1 所示结果十分接近JJG 188—2017《声级计检定规程》中所提到的参考值，即理想条件下不同档位的理论值。在实际测试中，由于所用仪器设备的不同，其测量误差难以估计，测试结果更加不可控。

表1 不同时间常数衰减速率

因此，本文提出一种基于拉普拉斯变换的混响时间优化算法，利用拉式变换对的数学性质，减小时间计权函数的影响，取得更高的混响时间测试精度。

2 基于数字信号处理的混响时间优化算法

2.1 混响时间优化算法

本文提出的优化算法，是拉普拉斯变换在混响时间测量中的一次应用。在上文公式（1）中，可以看到，时间计权的结果事实上为瞬时声压平方p2(ξ)与时间计权函数的卷积积分[8-9]。有：

其中pτ(ξ) 为ξ 相关的时间计权声压。

根据卷积定理[10]，对式2 进行S域变换，则有

式中：h(s)——时间计权函数的S域变换对；

p2(s)− 真实的声压平方值，通过计算p2(s)的衰减率，即可得到混响时间测量结果。

故而若要消除时间计权函数的影响，只需将时间计权声级和时间进行S域的变换，然后除去h(s)得到结果后再进行反变换，即可得到p2(t)[11-12]。流程如图3 所示。

图3 计算流程

2.2 算法输出结果

为验证算法实际效果，使用Matlab 对图示过程进行了模拟仿真。取一标准正弦信号，在700 ms处终止，时间谱（声压平方）如图4 所示。

图4 标准信号时间谱

取不同时间常数值，对其求时间计权，时间计权函数时间谱如图5 所示。

图5 时间计权函数时间谱

通过本文所述算法后，结果时间谱如图6 所示。

图6 处理结果时间谱

可以看到，在不同的时间计权函数作用下，最终输出结果曲线十分吻合，即证明优化后的算法可以消除时间计权函数对声压级测量结果的影响，进而能够实现更高精度的混响时间测量。

3 实验验证

3.1 实验环境及方法

为更能体现不同时间计权对混响时间的影响，实验在干扰较少，混响时间较短的房间中进行。将采集设备时间计权常数分别设置为1 s、1/2 s、1/4 s、1/8 s，重复测试四次获取四组实验数据。实验装置如图7 所示。

图7 实验装置

该实验装置由B&K 4943 型传声器、3160 型信号分析仪、PULSE 软件组成。混响时间的测试采用脉冲响应法进行，使用气球爆炸声作为声源激发房间响应。实验全过程依据GB/T 50076—2013《室内混响时间测量规范》进行，测得声压数据保存为.dat 格式文件，等待下一步处理。

3.2 实验数据分析

数据的后处理在Matlab 软件中进行，按时间常数的不同（1 s、1/2 s、1/4 s、1/8 s）分为四组，每组处理后的结果进行比较，以得到测量误差。实验时，设置设备采集时间为10 s。开始设备约4 s 时发出激发信号，不同时间常数时采集到的输出信号如图8所示。

图8 输出信号

时间常数越大，曲线更加平滑，但最终衰减速度更慢，对声压衰减曲线的影响就越大。分别采用四组信号输入算法，最终结果如图9 所示。

图9 结果输出

四组信号均能够完整的表现出激发信号的时域特征。比较四组结果，可以看到取不同的时间常数，最终结果仍然一致性较好，可以说明通过变换及反变换的过程后，声压测量结果可以较好的避免时间计权函数的影响，达到优化混响时间测量过程的目的。

4 结束语

在常用室内声学评价方法中，混响时间是最为关键的指标之一，而混响时间测量的基础是声压衰减曲线的测量。现有声学测量仪器往往通过时间计权的方式取得最终声压测试结果，时间常数的不同直接影响了声压测试结果。为解决这一问题，本文在研究现行测试方法的基础上，探讨了声压衰减曲线与混响时间的关系，利用数字信号处理方法获取了初始的声压信号，设计了算法处理流程，利用模拟信号验证了该算法的准确性。最后对算法进行了实验验证，实验结果表明，该方法能够减小时间计权函数对声压测试结果的影响，避免了因仪器设置不同引起的测量误差，对未来研究更高精度的混响时间测量方法具有一定的参考意义。