Pseudo-Predictor Feedback Control for Multiagent Systems with Both State and Input Delays

Qingsong Liu

Abstract—This paper is concerned with the consensus problem for high-order continuous-time multiagent systems with both state and input delays.A novel approach referred to as pseudopredictor feedback protocol is proposed.Unlike the predictorbased feedback protocol which utilizes the open-loop dynamics to predict the future states,the pseudo-predictor feedback protocol uses the closed-loop dynamics of the multiagent systems to predict the future agent states.Full-order/reduced-order observer-based pseudo-predictor feedback protocols are proposed,and it is shown that the consensus is achieved and the input delay is compensated by the proposed protocols.Necessary and sufficient conditions guaranteeing the stability of the integral delay systems are provided in terms of the stability of the series of retarded-type time-delay systems.Furthermore,compared with the existing predictor-based protocols,the proposed pseudo-predictor feedback protocol is independent of the input signals of the neighboring agents and is easier to implement.Finally,a numerical example is given to demonstrate the effectiveness of the proposed approaches.

I.INTRODUCTION

SINCE multiagent systems have very wide applications in many problem domains,such as,sensor networks [1],power systems [2] and social networks [3],cooperative control of multiagent systems has received considerable attention in the past two decades.Consensus problem is one of the most important fundamental problems in cooperative control of multiagent systems.With the development of the consensus theoretical framework for the multiagent systems[4],the consensus problem has been widely studied and many important results have been reported in the literature [5]–[8].For example,in the mixed environment of communication and broadcast,the consensus problem for the scalar multiagent systems was considered in [9],by developing the gain scheduling approach and the self-triggered mechanism,the consensus of continuous-time multiagent systems with actuator saturation was studied in [10],[11],for the secondorder multiagent systems,the finite-time consensus problem was considered in [12] and the necessary and sufficient conditions for the consensus were proposed in [13],and the(average)consensus problem for the multiagent systems was investigated in [14],[15].

Predictor-based feedback protocol is an efficient approach for studying the consensus problem of multiagent systems and the design of stabilizing controllers [16],and there are a large number of results reported in the literature.For instance,for multiagent systems with both input,output and/or communication delays,the leader-follower consensus problem was studied in [17] via the predictor based feedback protocols,and the consensus problem was addressed by the discrete-time predictor feedback protocols in [18],the observer-based predictor feedback approach was established in [19] to address the consensus problem of multiagent systems with input delays,for (nonlinear)multiagent systems with input delay,the consensus problem was considered by the Artstein reduction based predictor feedback approach in [20],and the same problem was studied via the truncated predictor feedback approach in [21],and the output/robust consensus for multiagent systems was investigated in [22]–[24] by some predictor-based feedback protocols.

Time delays related to information transmission cannot be ignored in practical applications.Input delay is one source of time delay since the packets arriving at each agent require the processing and connecting time [25].Generally,predictorbased state feedback protocols can be utilized to compensate the input delay such that the consensus is achieved in multiagent systems.Unfortunately,the predictor-based feedback protocols contain integral terms of the control input,thus involve the input signals of the neighboring agents (see,e.g.[20],[24] and [26])and may suffer some implementation problems [27],which is the main defect of the predictor-based feedback protocols.In order to circumvent this defect,for the continuous-time multiagent systems with both input and communication delays,the truncated predictor feedback protocol and the full-order observer-based truncated predictor feedback protocol were proposed in [28],and the reducedorder observer-based truncated predictor feedback protocol was later established in [29].Recently,the nested predictor feedback protocol and observer-predictor feedback protocol were respectively proposed in [30],[31] to study the consensus problem for discrete-time multiagent systems.

For the multiagent systems with both state and input delays,it is unfortunate that the predictor-based feedback protocols involve the input signals of the neighboring agents [20],[24],[26] and may suffer some implementation problems [27],and furthermore,the truncated predictor feedback protocol proposed in [28] may fail to solve the consensus problem.In order to overcome the main shortcoming of the predictorbased feedback protocols,the aim of this paper is to present an alternative protocol to consider the consensus problem for continuous-time multiagent systems with both state and input delays.Differently from the predictor-based feedback protocol which uses the open-loop dynamics to predict the future states,the proposed pseudo-predictor feedback protocol utilizes the closed-loop dynamics of the multiagent systems to predict the future agent states,and moreover,the proposed protocol is easier to implement since it is independent of the control signals of the neighboring agents and does not involve the integral terms of the control input.Full-order/reducedorder observer-based pseudo-predictor feedback protocols are also established,it is proved that the consensus is achieved and the input delay is compensated.In addition,necessary and sufficient conditions guaranteeing the stability of the integral delay systems are offered on the basis of the stability of the series of retarded-type time-delay systems.Finally,a numerical example is given to illustrate the effectiveness of the proposed protocols.

The remainder of this paper is organized as follows:In Section II,we give some preliminaries and the problem formulation.The pseudo-predictor feedback protocol is established in Section III.Full-order/reduced-order observerbased pseudo-predictor feedback protocols are established in Section IV.In Section V,a numerical example is worked out to support the obtained theoretical results,and Section VI concludes this paper.

Notations:The notations used in this paper are fairly standard.The identity matrix in Rn×nis denoted byIn.For two integerspandqwithp≤q,the symbol I [p,q] refers to the set{p,p+1,...,q}.Let L(f(t))denote the Laplace transformation of the time functionf(t).For a given complex number λ,λ∗is the conjugate of λ.The symbol ⊗ denotes the Kronecker product.For the variablexi∈Rn,denotes the predicted value ofxi(s),and,ifs≤0,then=xi(s).

II.PROBLEM FORMULATION AND PRELIMINARIES

A.Problem Formulation

We consider the following multiagent system with both state and input delays

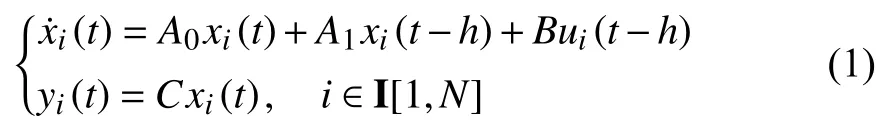
wherexi∈Rn,yi∈Rp,ui∈Rmdenote respectively the state,the output and the control of agenti,A0,A1∈Rn×nandB∈Rn×mare constant matrices,h>0 is the state/input delay,andN≥1 is a given integer,which denotes the number of agents.

In this paper,the weighted directed graph G(V,E,A)will be characterized as the communication topology among these agents,where V,E and A=[αij]∈RN×Ndenote the node set,the edge set and the weighted adjacency matrix,respectively,L=[lij]∈RN×Nis the corresponding Laplacian,and some other basic concepts and properties in graph theory can be found in [32].

We assume that agentireceives the state,output,and input information of its neighboring agents under the following rule:

wherei∈I[1,N].

The aim of this paper is to design pseudo-predictor feedback protocols and full-order/reduced-order observer-based pseudopredictor feedback protocols such that multiagent system (1)achieves consensus.Hence,we first recall the definition of consensus below.

Definition 1 [13]:The consensus of multiagent system (1)is achieved if=0,i,j∈I[1,N].

Now,the problems to be solved in the present paper can be stated as follows.

Problem 1:The consensus of multiagent system (1)can be achieved by the following designed pseudo-predictor feedback protocol

ui(t)=F1(χi(t+θ)),i∈I[1,N]

where θ∈[−h,0] and F1is a linear map.

Problem 2:The consensus of multiagent system (1)can be achieved by the following designed (full-order/reduced-order)observer-based pseudo-predictor feedback protocol

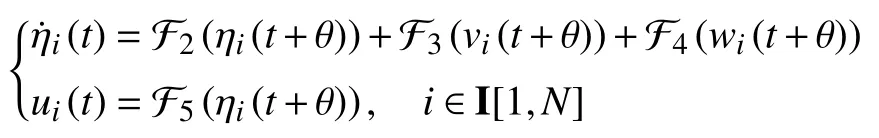
where θ∈[−h,0] and Fl,l∈I[2,5] are some linear maps,and moreover,limt→∞ηi(t)=0.

ForA1=0,Problems 1 and 2 were studied in [32] by the truncated predictor feedback protocol and observer-based output feedback protocols.It is worth mentioning that the truncated predictor feedback protocol proposed in [32] may fail to solve the consensus problem for the multiagent systems with both state and input delays.Notice that the problem was solved by the conventional predictor feedback protocol (see,e.g.[20],[24] and [26]).Unfortunately,the predictor-based feedback protocolsui(t)depend on the input signals of the neighboring agentsuj(t),j∈I[1,N],i≠j,and involve the history information of the neighboring agentsuj(t+θ),θ ∈[−h,0],j∈I[1,N][20],[24],[26].In addition,the resulting protocols contain integral terms,such as

which may suffer some implementation problems [27].In this paper,we will give a new solution to Problems 1 and 2 (see Section III and Section IV for details).

B.Preliminaries

In this subsection,we introduce some assumptions as follows.

Assumption 1:The weighted directed graphG(V,E,A)contains a directed spanning tree.

By the above assumption,there exists a nonsingular matrix Ψ=[1Nψ2··· ψN]∈CN×N,such that

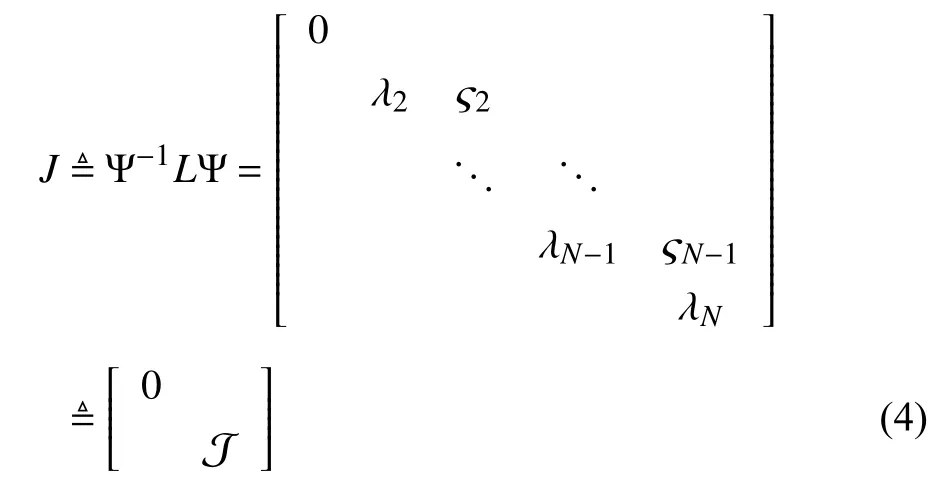
where λi,i∈I[1,N] denote the eigenvalues of the Laplacian matrixL,and ςi∈{0,1},i∈I[2,N−1].Let ςN=0.Assumption 1 implies that R e(λi)>0,i∈I[2,N].

In what follows,we give another assumption which is also satisfied in [30].

Assumption 2:There exist feedback gainsK0∈Rm×nandK1∈Rm×nsuch that,i∈I[1,N],

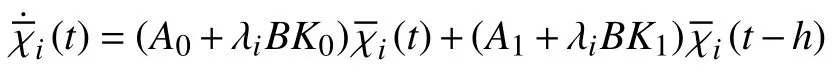
are asymptotically stable.

We mention that the design of the feedback gainsK0andK1in Assumption 2 is given by Lemma 1 in Appendix A,which is easily obtained by [33].

To design the full-order observer-based pseudo-predictor feedback protocols,we present the following assumption which is also satisfied in [30],[34].

Assumption 3:There exist two matricesF0∈Rn×pandF1∈Rn×psuch that

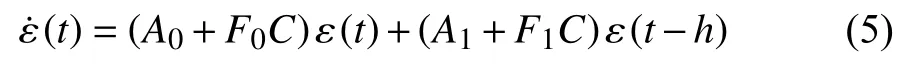
is asymptotically stable.

Notice that Assumption 3 is dual to Assumption 2 in the absence of λi.The design of the matricesF0andF1is given by Lemma 2 in Appendix A,which is easily obtained by applying Lemma 1 in Appendix A.

In order to design the reduced-order observer-based pseudopredictor feedback protocols,we give the following assumption which is also satisfied in [30],[34].

Assumption 4:There exist two matricesE0∈R(n−p)×(n−p)andE1∈R(n−p)×(n−p)such that

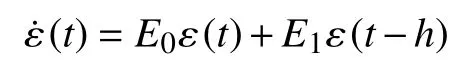
is asymptotically stable.

III.PSEUDO-PREDICTOR BASED STATE FEEDBACk PROTOCOLS

In this section,we will establish the pseudo-predictor based state feedback protocol to solve Problem 1.Notice that

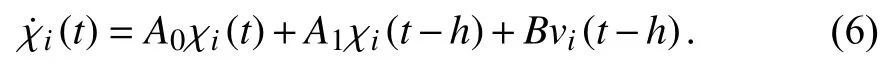
Design a predictor-based feedback protocol as

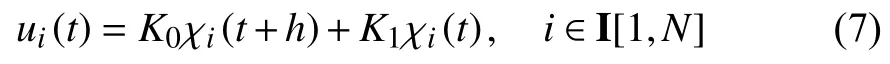
Clearly,we need to predict χi(t+h),i∈I[1,N] in (7).It then follows from the open-loop system (6)that χi(t+h),i∈I[1,N]can be predicted as

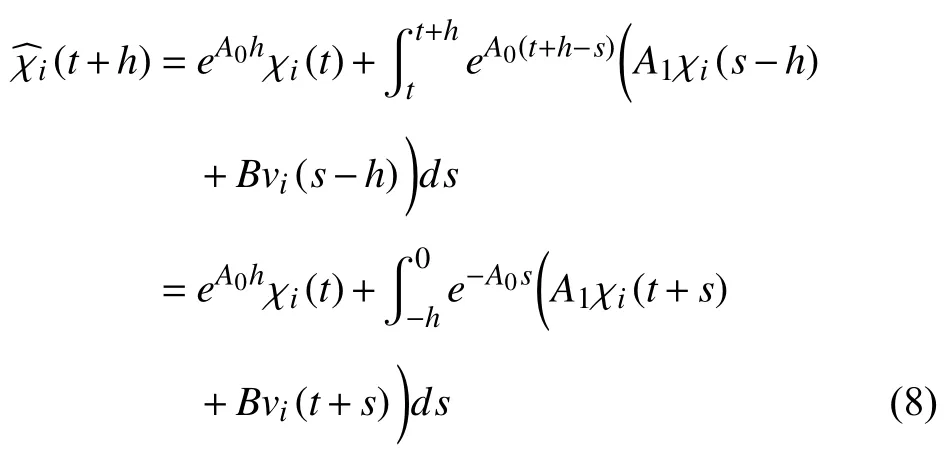
by which,we can get

However,protocol (9)depends on the signalsuj(t),j∈I[1,N],i≠j,and involves the history information ofuj(t+θ),θ ∈[−h,0],j∈I[1,N],and moreover,since protocol(9)contains integral terms (3),it may suffer some implementation problems [27].To solve this problem,we develop the pseudo-predictor feedback approach as follows[35],namely,using the closed-loop dynamics of the multiagent systems

instead of (6)to predict the future agent states χi(t+h).By virtue of (8),whereA0is replaced by,A1is replaced by,andvi=0,we get

which is referred to as pseudo-predictor feedback protocol.

To go further,define the following variables as

The following theorem shows that the consensus of multiagent system (1)can be achieved by the pseudo-predictor feedback protocol (12).

Theorem 1:Let Assumptions 1 and 2 be satisfied.Then,Problem 1 is solved by the pseudo-predictor feedback protocol(12)if the integral delay systems (IDSs)

are all asymptotically stable.

Proof:Notice that the characteristic equations for system(10)and IDSs (14)can be written as,respectively

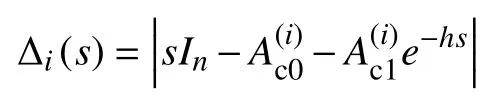
and

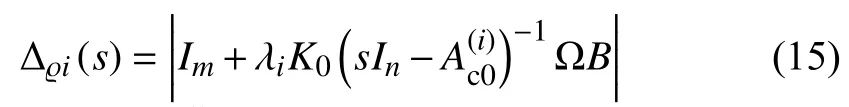
where Ω=In−.Clearly,multiagent system (6)and(7)can be rewritten as

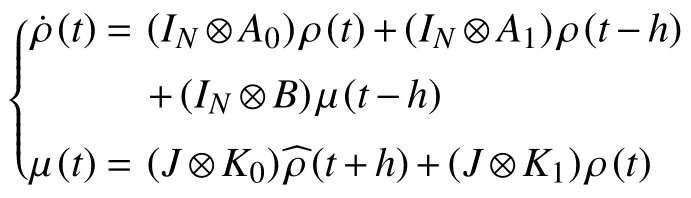
where ρ and µ are defined respectively by

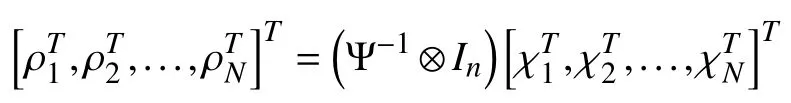
and

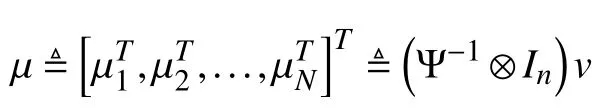
It follows that

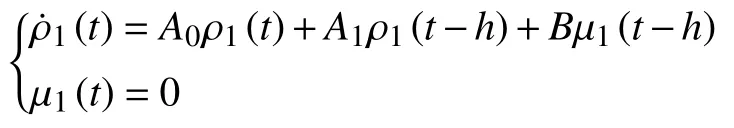
and

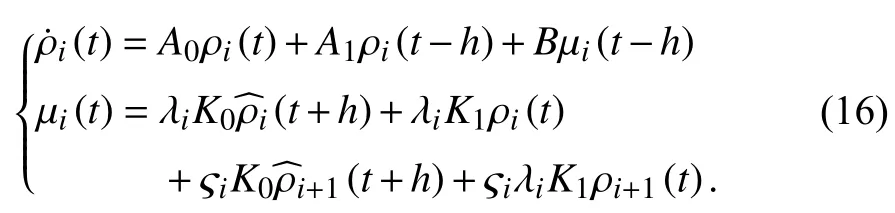
Notice that the closed-loop system (16)is the upper triangular structure.Then,we can get that system (16)is asymptotically stable if and only if

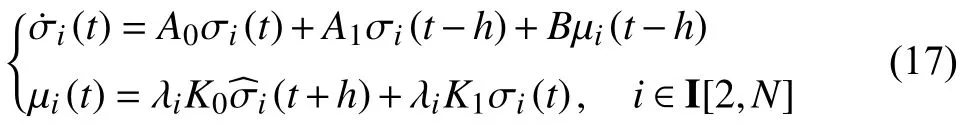
are asymptotically stable,wherecan be predicted by the closed-loop dynamics of the multiagent systems,namely

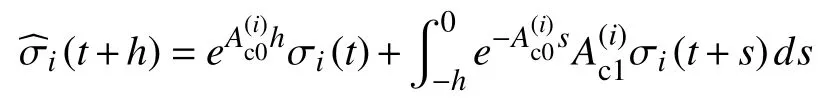
in which

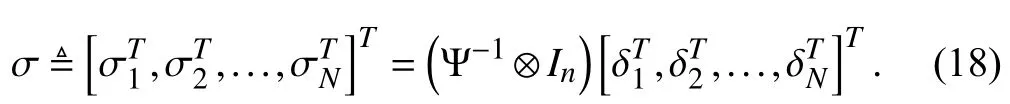
Note that

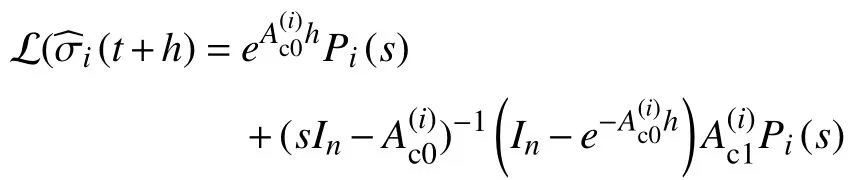
wherePi(s)=L(σi(t)),by which,system (17)in the frequency domain can be represented as

whereUi(s)=L(µi(t)),i∈I[2,N],and

The characteristic equation of system (19)is then given by[36]

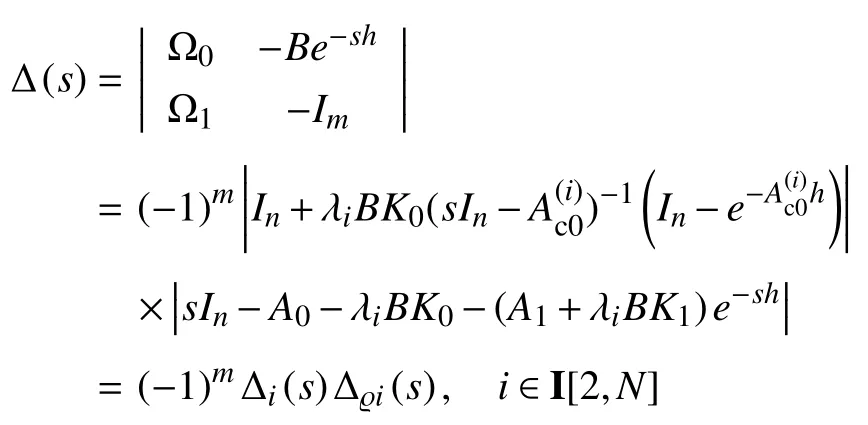
where we have noticed that det(In+MN)=det(Im+NM)withMandNhaving appropriate dimensions.Hence,it follows from Assumption 2 that

By (4),(13)and (18),we can get

where

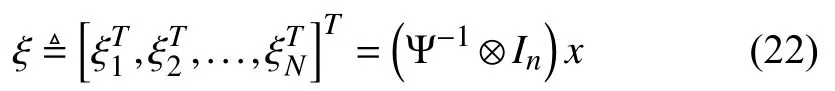
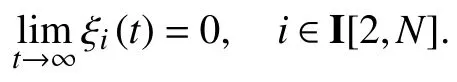
Then,we have limt→∞∥xi(t)−ξ1(t)∥=0,i∈I[1,N] as the first column of Ψ is 1Nandx(t)=(Ψ⊗In)ξ(t). ■

At the end of this section,the necessary and sufficient conditions guaranteeing the stability of IDSs (14)are obtained by the following corollary.

Corollary 1:Under the assumption thatis Hurwitz,IDSs (14)are asymptotically stable if and only if

are asymptotically stable.

Proof:Notice that

which is exactly the characteristic equation for system (23),where Ω is defined in the proof of Theorem 1,we have noticed that (15)and det(In+MN)=det(Im+NM) withMandNhaving appropriate dimensions. ■

Obviously,the pseudo-predictor feedback protocol (12)is independent of the signalsuj(t),j∈I[1,N],i≠j,and does not contain the history information ofuj(t+θ),θ ∈[−h,0],j∈I[1,N]and the integral term (3).

IV.OBSERvER-BASED PSEUDO-PREDICTOR FEEDBACk PROTOCOLS

In this section,we will solve Problem 2 by designing the observer-based pseudo-predictor feedback protocols.In terms of (1)and (13),we have

Now,we present the main results in this section by the following theorem.

Theorem 2:Let Assumptions 1–3 be satisfied.Then,Problem 2 is solved by the following protocol:

Moreover,limt→∞∥ηi(t)∥=0,i∈I[1,N].

Proof:In view of (13),we have

where σ and ξ are defined respectively by (18)and (22).It follows from (4)and (26)that σ1(t)=0,

where ξN+1(t)=0.Define the new variables as

By (24)and (25),we get

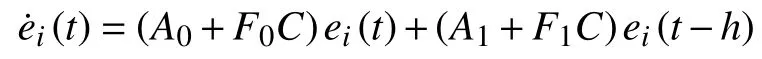
which implies that limt→∞∥ei(t)∥=0,i∈I[1,N] with the help of Assumption 3.Consider the following artificial protocol

it then follows from (24)that

by which,we can further get

wheres∈[−2h,0] and Φ is a linear map.We note that system(30)is equivalent to=A0σ1(t)+A1σ1(t−h)and

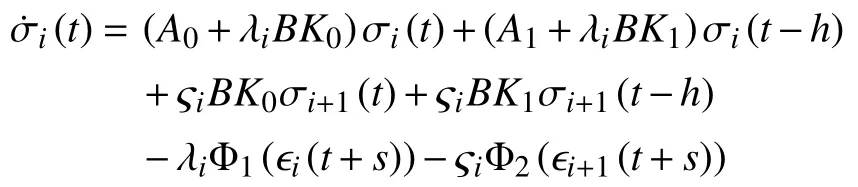
wherei∈I[2,N],σN+1=0,ϵN+1=0,(Ψ−1⊗In)e,and Φ1and Φ2are some linear maps.It follows from Assumption 2 that

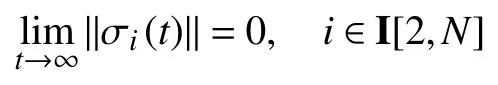
where we have noticed that σ1(t)=0 and limt→∞∥ei(t)∥=0,i∈I[1,N].By (27),we can get limt→∞∥ξi(t)∥=0,i∈I[2,N].Hence,we can further get

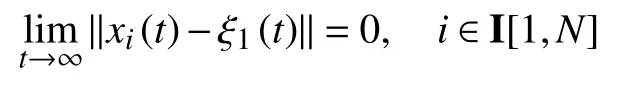
which means that the consensus is achieved.In addition,we have

where we have used limt→∞∥ei(t)∥=0 and limt→∞∥δi(t)∥=0,i∈I[1,N].

In view of (29),we notice that

which is equivalent to the protocolui(t)in (25)with the help of (28). ■

Notice that the full-order observer-based pseudo-predictor feedback protocol is designed in Theorem 2.We mention that the consensus problem can also be solved by designing the reduced-order observer-based pseudo-predictor feedback protocol.

Now,we present the main results by the following corollary,whose proof is moved to Appendix B.

Corollary 2:Let Assumptions 1,2 and 4 be satisfied.Then,Problem 2 is solved by the following reduced-order observerbased pseudo-predictor feedback protocol:

where (H,Pi,Pi,Ri,Ri,Qi,Qi,) satisfiesHA0−E0H=T0CandHA1−E1H=T1C,and

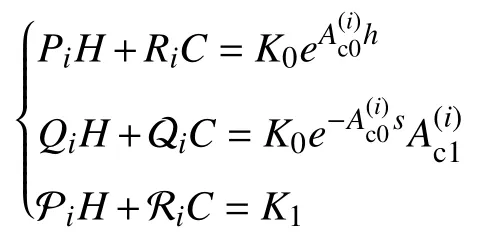
in whichi∈I[1,N] ands∈[−h,0].Moreover,limt→∞∥ζi(t)∥=0,i∈I[1,N].

V.A NUMERICAL EXAMpLE

In this section,a numerical example is offered to illustrate the effectiveness of the proposed protocols.We consider four agents whose dynamics obeys the form of (1),where the coefficient matrices are set as

andh=0.5.Let the weighted directed network be given by Fig.1,the corresponding Laplacian matrix is presented by

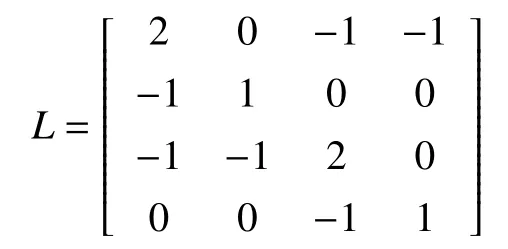
and the eigenvalues of Laplacian matrixLare 0,2,2 and 2.

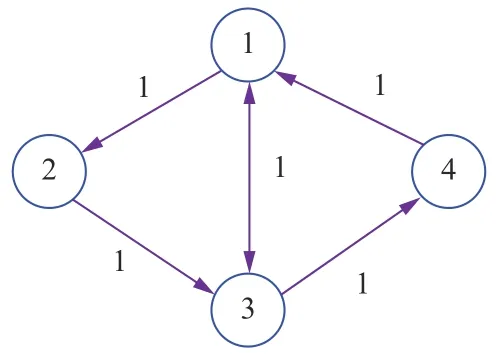
Fig.1.Communication network.

1)Pseudo-Predictor Feedback Protocol:By virtue of Lemma 1 in Appendix A,the feedback gain matricesK0andK1are given by

K0=[−0.0096−0.6993 0.0845−0.4349]

K1=[0.0007−0.9785−0.0087 0.0227].

The initial conditions for the four agents are set asx1(0)=[1,−1,2,−3]T,x2(0)=[−2,1,−2,1]T,x3(0)=[−1,−2,1,2]Tandx4(0)=[2,1,−3,−1]T.The states trajectories ofxij−x1j,i∈I[2,4],j∈I[1,4] are recorded in Fig.2.The consensus of this multiagent system is clearly achieved and the input delay is compensated by the proposed pseudopredictor feedback protocol.To compare with the predictorbased feedback protocols,the states trajectories ofxij−x1j,i∈I[2,4],j∈I[1,4] for this multiagent system (1)with protocol (9)are also recorded in Fig.3.Unfortunately,the consensus of this multiagent system is not achieved by protocol (9).

2)Observer-Based Pseudo-Predictor Feedback Protocol:In virtue of Lemma 2 in Appendix A,the observer gain matricesF0andF1can be designed as

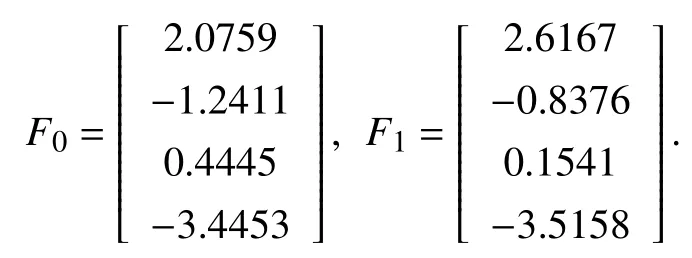
The initial conditions for the observer are set as η1(0)=[2,1,1,−2]T,η2(0)=[−1,−1,−1,2]T,η3(0)=[−2,−3,2,1]Tand η4(0)=[1,2,−2,−1]T.The states trajectories ofxij−x1j,i∈I[2,4],j∈I[1,4] are recorded in Fig.4,and the states trajectories of the observers are recorded in Fig.5.Obviously,the consensus is factually achieved and the input delay is compensated by the proposed observer-based pseudopredictor feedback protocol.

By comparing Fig.2 with Fig.3,we can see that the consensus of this multiagent system is factually achieved by the proposed pseudo-predictor feedback protocol,and it is unfortunate that the consensus of this multiagent system is not achieved by the predictor-based feedback protocol (9).In addition,according to Figs.2,4 and 5,we can observe that the convergence rate ofxij−x1jcontrolled by the proposed pseudo-predictor feedback protocol is obviously faster than that controlled by the proposed observer-based pseudopredictor feedback protocol.

VI.CONCLUSIONS

This paper studied the consensus problem of continuoustime multiagent systems with both state and input delays.Differently from the conventional predictor feedback which utilizes the open-loop system to predict the future states,the proposed pseudo-predictor based state feedback protocols and full-order/reduced-order observer-based pseudo-predictor feedback protocols use the closed-loop dynamics of the multiagent systems to predict the future agent states,it was revealed that the consensus was achieved and the input delay was compensated,and the proposed protocol was independent of the control signals of the neighboring agents and was easier to implement than the existing predictor-based protocols.Moreover,necessary and sufficient conditions guaranteeing the stability of the integral delay systems were established in the light of the series of retarded-type time-delay systems.A numerical example was worked out to support the obtained theoretical results.

AppENDIX A THE DESIGN OF THE FEEDBACk GAINS

Lemma 1:If there exist symmetric matricesP>0,Q>0,Z>0,and two matricesG0andG1such that

Fig.2.Differences between the states of Agent 1 and those of other agents (pseudo-predictor feedback protocol).

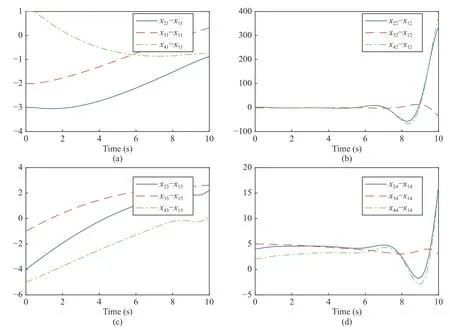
Fig.3.Differences between the states of Agent 1 and those of other agents (predictor-based feedback protocol).

are feasible,i∈I[1,N],then linear time-delay systems (10)are asymptotically stable,where Ω2=.Moreover,K0=G0P−1andK1=G1P−1.

Lemma 2:If there exist symmetric matricesP>0,Q>0,Z>0,and two matricesU0andU1such that

is feasible,then linear time-delay system (5)is asymptotically stable,where Θ=.Moreover,F0=P−1U0andF1=P−1U1.

AppENDIX B THE PROOF OF COROLLARY 2

Proof:Letei(t)=ζi(t)−Hδi(t),it then follows from (24)and (31)that

Fig.4.Differences between the states of Agent 1 and those of other agents (observer based output feedback protocol).

Fig.5.States of the observer.

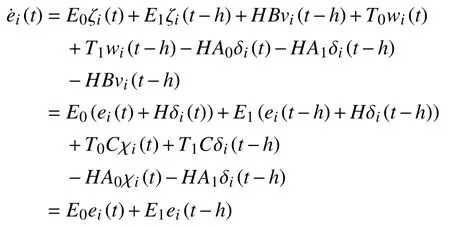
which implies limt→∞∥ei(t)∥=0,i∈I[1,N] in terms of Assumption 4.Consider the following artificial protocol:

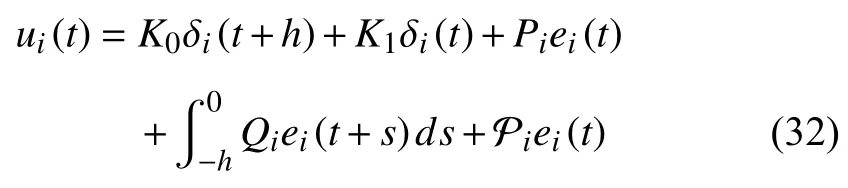
it yields from (24)that

Then,

wheres∈[−2h,0] and Φ0is a linear map.We note that system(33)is equivalent to=A0σ1(t)+A1σ1(t−h)and

wherei∈I[2,N],σiand ϵihave been defined in the proof of Theorem 2,σN+1=0,ϵN+1=0,and Φ3and Φ4are some linear maps.It yields from Assumption 2 that

where we have noticed that σ1(t)=0 and limt→∞∥ei(t)∥=0,i∈I[1,N].By (27),we can getlimt→∞∥ξi(t)∥=0,i∈I[2,N].Hence,we can further get

which means the consensus is achieved.In addition,we have limt→∞∥ζi(t)∥=0,i∈I[1,N],with the help of limt→∞∥ei(t)∥=0 and limt→∞∥δi(t)∥=0,i∈I[1,N].Finally,by (32),we note that