基于广义S变换的透射槽波埃里相识别
2021-10-23陈波朱国维武延辉杨振强周俊杰
陈波,朱国维,武延辉,杨振强,周俊杰
(1.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083; 2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室,北京 100083)
0 引言
我国煤炭资源丰富,分布广[1],但煤层赋存地质条件差,致灾因素较多,而地面地震勘探精度低,无法满足煤矿企业对安全生产的需求,因此在煤矿工作面内开展透射地震勘探为精细查明工作面内的地质情况提供了可能[2-3]。相对于围岩,煤层速度低,在煤层内激发地震波会产生沿煤层传播的槽波[4-5]。由于在煤层内传播的槽波携带了煤层的地质信息,因此通过对透射槽波的分析可以查明工作面内的地质异常。频散是透射槽波的重要特征,埃里相分布在频散曲线上速度最低能量强的位置,其特征明显,通过对频散曲线埃里相的分析可以获得工作面内煤层的速度及厚度[6-8],从而查明工作面内的地质情况。因此,准确地从透射槽波频散曲线中识别埃里相显得尤为关键。
目前,频散曲线的提取方法主要有基于单道分析的多次滤波法、移动时窗法、时频分析法及基于多道分析的F-K域变换和拉东变换等[6]。在透射槽波的分析中,需要对单道槽波提取频散曲线,研究高精度的单道频散曲线的提取方法对透射槽波分析具有重要意义。Feng和Zhang[9]提出了时窗可变的S变换提取透射槽波频散曲线,取得了较好效果,但未讨论如何准确识别埃里相。笔者受Li等[10]的启发,将广义S变换引入到透射槽波的频散曲线提取中,并对参数的取值做出分析,通过选取合理参数突出埃里相特征,确保准确地识别出频散曲线中的埃里相。
1 广义S变换
Stockwell等[11]提出了S变换,其定义式如下:
(1)
其逆变换为:
(2)
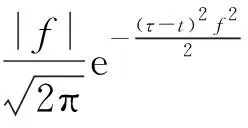
Li等[10]构造了一种形式更为简洁的两参数广义S变换并展示了其良好的应用效果,定义式如下[10]:


图1 广义S变换窗函数时间半高宽随频率变化Fig.1 Temporal FWHM of generalized S-transform window versus frequency
(4)
(5)
式中:f1、f2为频率,tFWHM1、tFWHM2为窗函数时间半高宽。当频率为f1时,窗函数的时间半高宽为tFWHM1;当频率为f2时,窗函数的时间半高宽为tFWHM2。附录A给出了详细推导,可以通过给定两个频率点的时间半高宽快速确定A和B。
为检验广义S变换在提高信号时频分辨率方面的性能,利用合成信号进行了初步测试,图2a为频率呈阶梯变化的非平稳信号[22],其中前部分为低频并包含一个高频信号,中间部分为中频,后部分为高频,信号的具体表达式如式(6)所示:

(6)
图2b、2c分别为图2a所示信号的S变换和广义S变换结果,从变换的结果可以看到,广义S变换信号的频率分辨率显著提高,在时频域中,阶梯状信号的能量聚集性更好,即频率分辨率提高,由海森堡不确定性原理,其时间分辨率降低,图2c中持续时间较短的高频信号能量相对发散,表明了其时间分辨率降低。图2d展示了图2b和图2c虚线处的线谱,相比S变换,广义S变换信号能量更集中,频率分辨率得到大幅提高。图2e为50 Hz时的S变换和广义S变换窗函数比较,广义S变换窗函数呈现出“矮”、“宽”特征,图2f为窗函数时间半高宽对比图,广义S变换窗函数整体比S变换宽,因此,其频率分辨率高于S变换。任取两点,由式(4)和式(5)即可确定A、B值,本例中A=0.4239、B=0.471。

a—频率阶梯变化的非平稳信号;b—图2a的S变换结果;c—图2a的广义S变换结果;d—图2b、图2c虚线处的线谱;e—50 Hz时的S变换和广义S变换窗函数振幅随时间变化;f—S变换和广义S变换窗函数时间半高宽对比a—non-stationary signal with frequency step change;b—S-transform results of Fig. 2a;c—generalized S-transform results of Fig. 2a;d—line spectra at dotted lines in Fig. 2b and Fig. 2c;e—S-transform and generalized S-transform window amplitude versus time at 50 Hz;f—comparison of the temporal FWHM between S-transform and generalized S-transform图2 频率阶梯变化的非平稳信号的S变换和广义S变换(A=0.4239,B=0.471)对比分析Fig.2 Comparison of S-transform and generalized S-transform (A=0.4239,B=0.471) for non-stationary signal with frequency step change
2 合成数据应用
利用文献[23]给出的Love型槽波计算方法合成槽波,计算参数如表1所示。

表1 合成Love型槽波物性参数
合成的Love型槽波如图3a所示,道间距为5 m,共41道。取第30道进行群速度频散曲线提取,提取过程简述如下:
首先将地震道变换到时频域S(t,f),然后用炮检距x除以t,即得v=x/t,最后对S(v,f)重新排序并插值得到群速度频散曲线图。
图3b为第30道Love型槽波记录,图3c为图3b数据S变换提取的群速度频散曲线图,其中星号线为Love型槽波群速度理论频散曲线[24-25](下同),由图可见,提取的频散曲线与理论频散曲线一致性较好,说明了提取的频散曲线的正确性。在本例中,广义S变换的目的是适度提高提取的频散曲线频率分辨率,突出埃里相特征。图3d为图3b数据广义S变换结果,从图可知,频散曲线埃里相(图3c、3d黑色圆圈所示区域,下同)能量聚集性明显比S变换更好,更利于准确快速拾取埃里相。本例中,广义S变换A、B值与图2一致,广义S变换的目的都是适度提高频率分辨率。
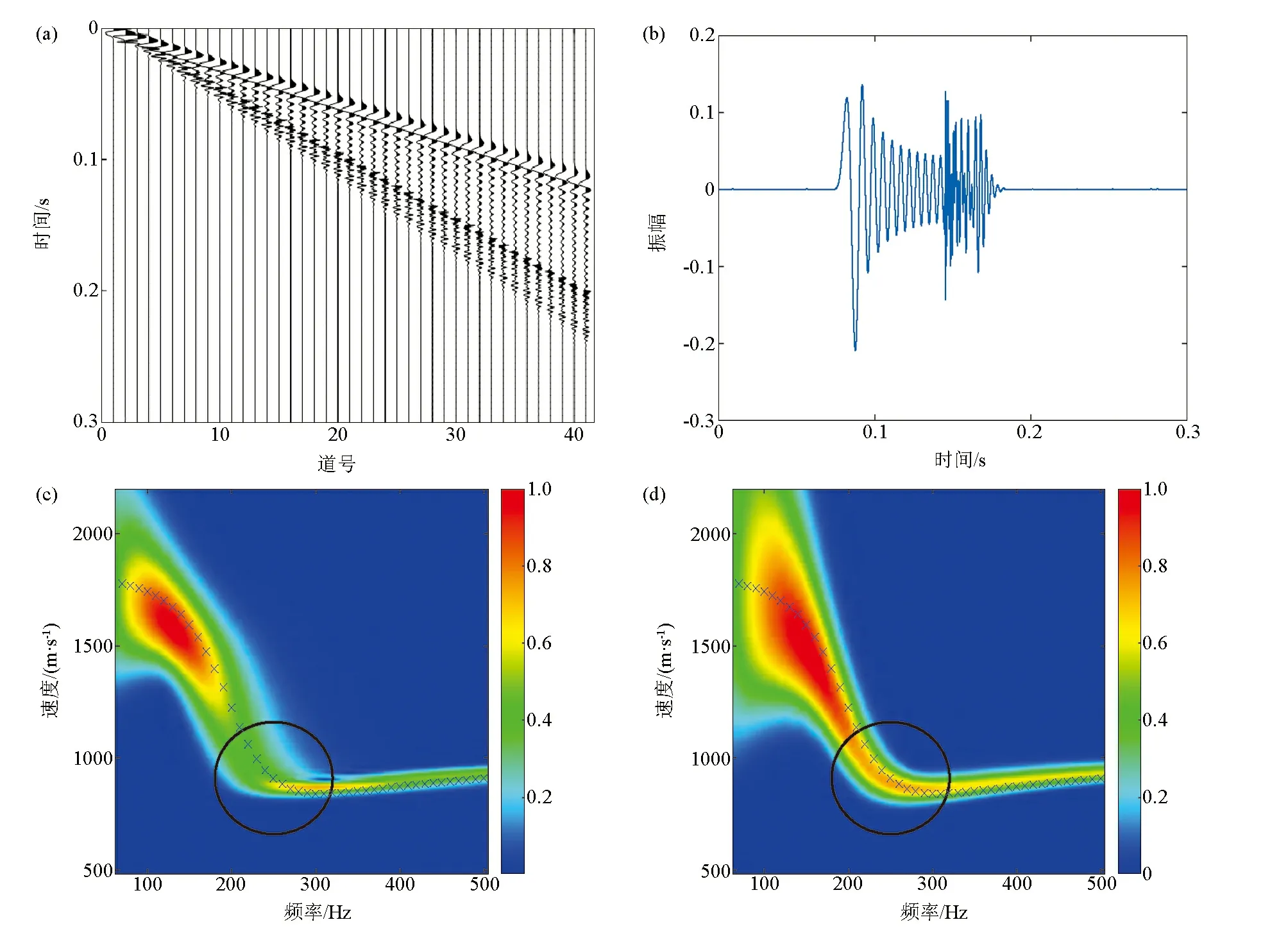
a—合成Love型槽波记录;b—图3a中第30道槽波记录;c—图3b数据S变换提取的频散曲线;d—图3b数据广义S变换提取的频散曲线a—synthetic Love channel waves;b—the 30th channel wave in Fig. 3a;c—dispersion curve of Fig. 3b extracted by S-transform;d—dispersion curve of Fig. 3b extracted by generalized S-transform图3 合成Love型槽波数据S变换和广义S变换(A=0.4239,B=0.471)提取频散曲线对比分析Fig.3 Comparison of the dispersion curve extracted by S-transform and generalized S-transform (A=0.4239,B=0.471) for synthetic Love channel waves
为进一步说明广义S变换A、B取值对频散曲线埃里相特征的影响,与图3相反,我们取一组值A=2.1195、B=2.355,使广义S变换窗函数时间半高宽整体比S变换窄,广义S变换窗函数呈现出“高”、“窄”特征,如图4a所示,图4b为窗函数时间半高宽对比,广义S变换窗函数整体比S变换窄,其时间分辨率高于S变换,由海森堡不确定性原理,频率分辨率低于S变换。利用此广义S变换对图3b数据进行处理,提取的群速度频散曲线如图4c所示(埃里相所在区域由黑色圆圈所示),可以看到,相比S变换提取的群速度频散曲线图3c,图4c中埃里相所在区域黑色圆圈所示完全无法识别,因此,通过图3、图4的分析可知,利用广义S变换适度提高频率分辨率更有利于埃里相的识别。
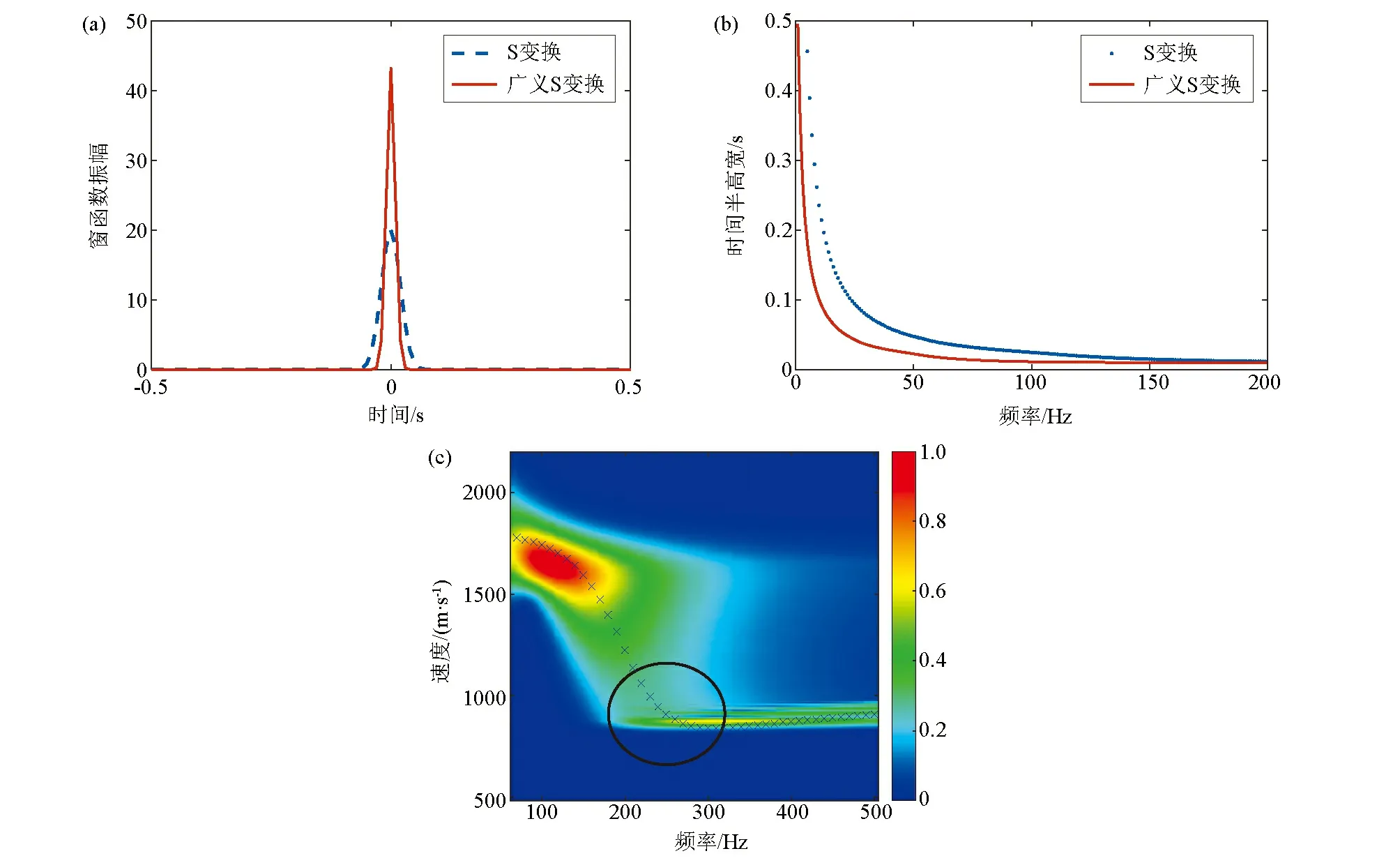
a—50 Hz时的S变换和广义S变换窗函数振幅随时间变化;b—S变换和广义S变换窗函数时间半高宽对比;c—图3b所示数据广义S变换提取的频散曲线a—S-transform and generalized S-transform window amplitude versus time at 50 Hz;b—comparison of temporal FWHM between S-transform and generalized S-transform;c—dispersion curve of Fig. 3b extracted by generalized S-transform图4 合成Love槽波数据广义S变换(A=2.1195,B=2.355)提取频散曲线Fig.4 Dispersion curve extracted by generalized S-transform (A=2.1195,B=2.355) for synthetic Love channel waves
为测试广义S变换在含噪情况下对数据的处理能力,在图3a所示的数据中加入随机噪声,得到如图5a所示数据。图5a中第30道槽波记录如图5b所示,对图5b所示数据进行S变换和广义S变换分析,广义S变换A、B值与图3取值一致,图5c为S变换提取的频散曲线,图5d为广义S变换提取的频散曲线,两种方法提取的频散曲线与理论频散曲线一致性均较好,但广义S变换提取的频散曲线埃里相更易于识别,进一步说明广义S变换在数据含噪情况下也能突出埃里相特征。
3 实际资料应用
图6a为某工作面第12炮第10道透射槽波记录,图6b、6c分别为图6a数据S变换和广义S变换(A=0.4239,B=0.471)提取的频散曲线,从两图对比看到,相比图6b,图6c埃里相能量更集中,群速度频散曲线埃里相特征更明显,可以迅速确定埃里相位于图6c中黑色圆圈所示区域,而从图6b所示频散曲线图中识别埃里相则相对困难。因此,广义S变换提取的频散曲线更有利于准确拾取透射槽波埃里相,使解释人员能较快速地识别埃里相频率及速度,从而为下一步工作面层析成像研究奠定坚实基础。
4 结论
1)讨论了广义S变换中参数的取值与时频分辨率的关系,并推导了其参数与窗函数时间半高宽的具体表达式,为定量表征时频分辨率奠定基础。
2)广义S变换的数值试验表明,通过合理选择参数,广义S变换能够有效提高时间或频率分辨率,根据海森堡不确定性原理,在提高频率分辨率的同时,时间分辨率会有所下降,反之亦然,因此,需根据实际情况合理选择参数,提高时频分辨率。
3)将广义S变换引入到透射槽波频散曲线提取中,研究认为广义S变换能有效改善频散曲线的时频分辨率,通过选取合适的参数能进一步有效突出频散曲线中埃里相特征,使解释人员能准确快捷地识别透射槽波埃里相。

a—图3a加入随机噪声后的Love型槽波记录;b—图5a中第30道槽波记录;c—图5b数据S变换提取的频散曲线;d—图5b数据广义S变换提取的频散曲线a—synthetic Love channel waves with adding random noise to Fig. 3a;b—the 30th channel wave in Fig. 5a;c—dispersion curve of Fig. 5b extracted by S-transform;d—dispersion curve of Fig. 5b extracted by generalized S-transform图5 合成Love槽波数据中加入随机噪声后S变换和广义S变换(A=0.4239,B=0.471)提取频散曲线对比分析Fig.5 Comparison of the dispersion curve extracted by S-transform and generalized S-transform (A=0.4239,B=0.471) for synthetic Love channel waves with adding random noise
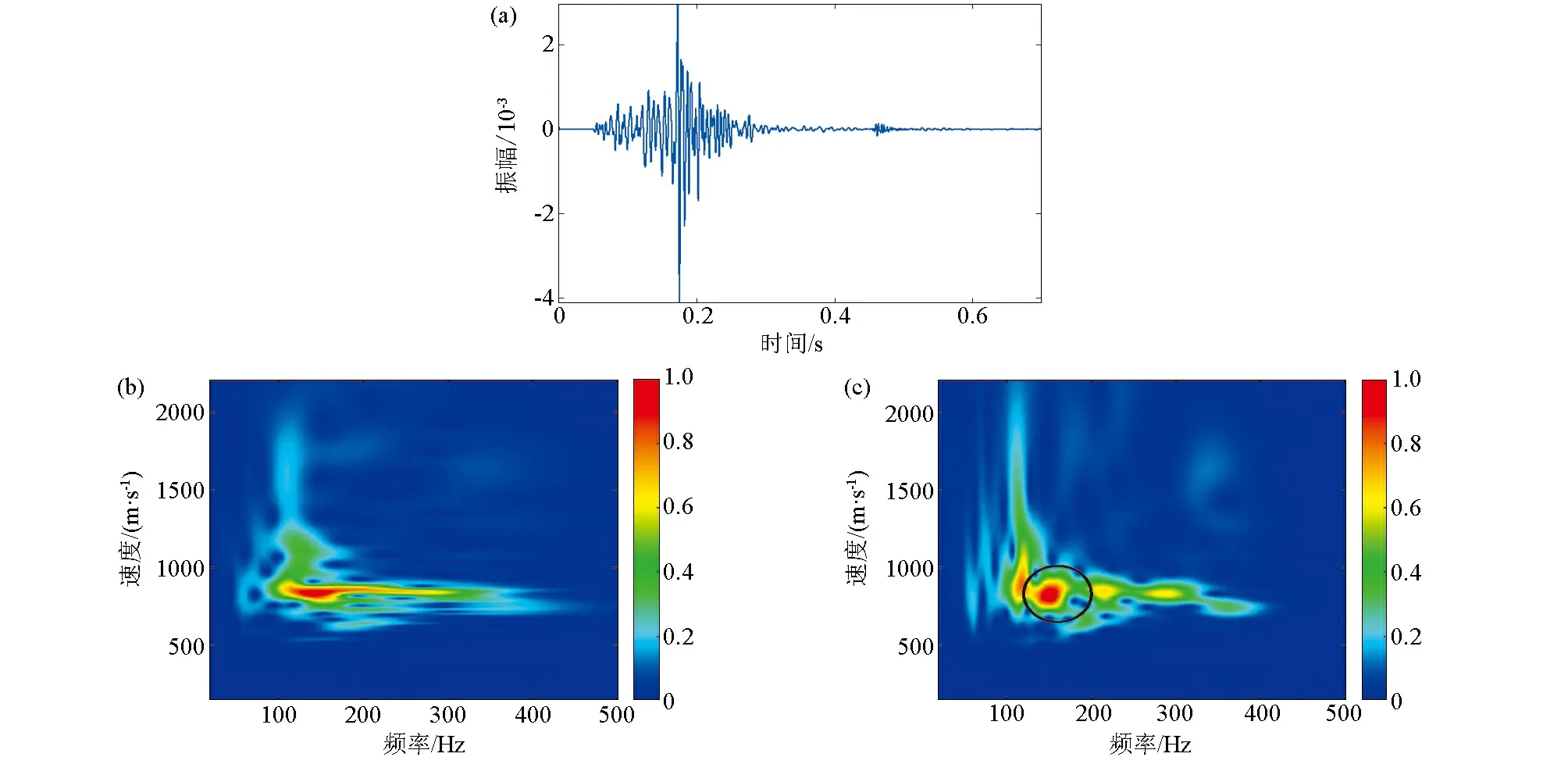
a—某工作面第12炮第10道透射槽波记录;b—图6a数据S变换提取的频散曲线;c—图6a数据广义S变换提取的频散曲线a—the 10th transmitted channel wave of the 12th shot in a coal mining face;b—dispersion curve of Fig. 6a extracted by S-transform;c—dispersion curve of Fig. 6a extracted by generalized S-transform图6 实际槽波数据的S变换和广义S变换(A=0.4239,B=0.471)提取频散曲线对比分析Fig.6 Comparison of the dispersion curve extracted by S-transform and generalized S-transform(A=0.4239,B=0.471) for real data
