一类新的随机三项共轭梯度算法
2021-10-23北京邮电大学理学院北京100876
杨 晗(北京邮电大学 理学院,北京100876)
深度学习概念最早由Hinton等人为研究人脑多层次的抽象学习过程而提出,为此他们提出了多层神经网络结构.近年来,深度学习作为一种新的机器学习模型受到广泛关注并在各个领域中得到了应用,在语音识别[1]、图像处理[2]、数据挖掘[3]、计算机视觉[4]、自然语言处理[5]等场景下均有良好表现.
深度学习模型主要是由输入层、多层隐藏层和输出层构成,该网络结构的隐藏层含有大量参数,在实际训练过程中需要修正这些参数,从而出现经验风险最小化问题(ERM).针对这一优化问题,为了减少计算量,目前人们提出的大量有关深度学习的优化算法主要是随机梯度下降法(SGD)和对其的改进算法.在确定性的优化方法中,共轭梯度算法由于具有计算量小,存储量小,计算效果好等优点而被广泛应用.因此对于ERM问题,人们将共轭梯度法成功应用在训练神经网络上,并有学者提出了随机共轭梯度算法.三项共轭梯度方法比传统两项共轭梯度方法在理论和数值上均有更优表现,因此本文提出一类新的随机三项共轭梯度算法,并在不同问题和数据集上进行数值实验,论证新算法在求解ERM问题上的有效性.
1 问题描述与经典方法
1.1 经验风险最小化问题
深度学习中的优化过程是由预测函数和损失函数给出的,网络结构如图1所示,由输入层,隐藏层和输出层构成,隐藏层的所有参数记为向量ω.

图1 网络结构
对于输入值x,经过网络隐藏层计算后会产生预测值h(x;ω),损失函数l(h(x;ω),y)用来衡量真实值y与预测值h(x;ω)之间的差距.
理想情况下,为了使任何输入-输出对产生的损失函数值最小而选择合适的参数向量ω,假设概率分布P(x;y)表示输入和输出之间的真实关系,即输入-输出空间Rdx×Rdy服从概率分布P(x;y).Rdx×Rdy→[0,1],以此定义期望风险函数:
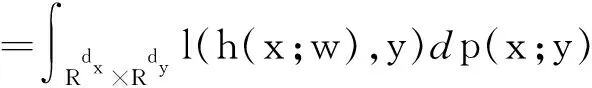
=E[l(h(x;w),y)]
(1)

(2)
即每个样本损失函数的平均值.极小化式(2)为所求优化问题,称为经验风险最小化(ERM)问题.
为了表示方便,将ERM问题写成
(3)
其中:n为样本个数,fi(ω)为第i个样本的损失函数.
1.2 随机梯度下降类算法
一般情况下,问题(3)中样本数量巨大,即n的值非常大,所以考虑随机算法.
目前常用的随机算法为随机梯度下降法(SGD)[6]和小批量版本的随机梯度下降法(mini-SGD)[7],它们的更新格式分别为:
ωk+1=ωk-αkgk=ωk-αkfζk(ωk)
其中:ζk为从n个样本中随机选取的一个,Sk为随机选取的一部分,称为小批量,|Sk|表示小批量中样本个数.这两种方法都可以减少对梯度的计算量,但是由于对梯度的估计是随机的,与真实的梯度之间有一个比较大的方差,这个方差会导致收敛速度较慢.特别地,即使在目标函数f(ω)为强凸函数时,也只能达到次线性收敛速度[8].
为了提高收敛速度,Johnson等人[9]提出了一种方差缩减的随机梯度下降法(SVRG),它的主要迭代格式如下:
ωt+1=ωt-αgt

2 随机共轭梯度算法
2.1 三项共轭梯度算法
共轭梯度法[10]是求解大规模无约束优化问题
min{f(ω)|ω∈Rd}
的一类简单高效的计算方法,其迭代公式为:
ωk+1=ωk+αkpk
其中:gk=f(ωk),αk是步长,通常由某种非精确线搜索产生.常用的线搜索有很多种,本文只考虑强Wolfe线搜索条件:
f(ωk+αkpk)≤f(ωk)+c1αkf(ωk)Tpk
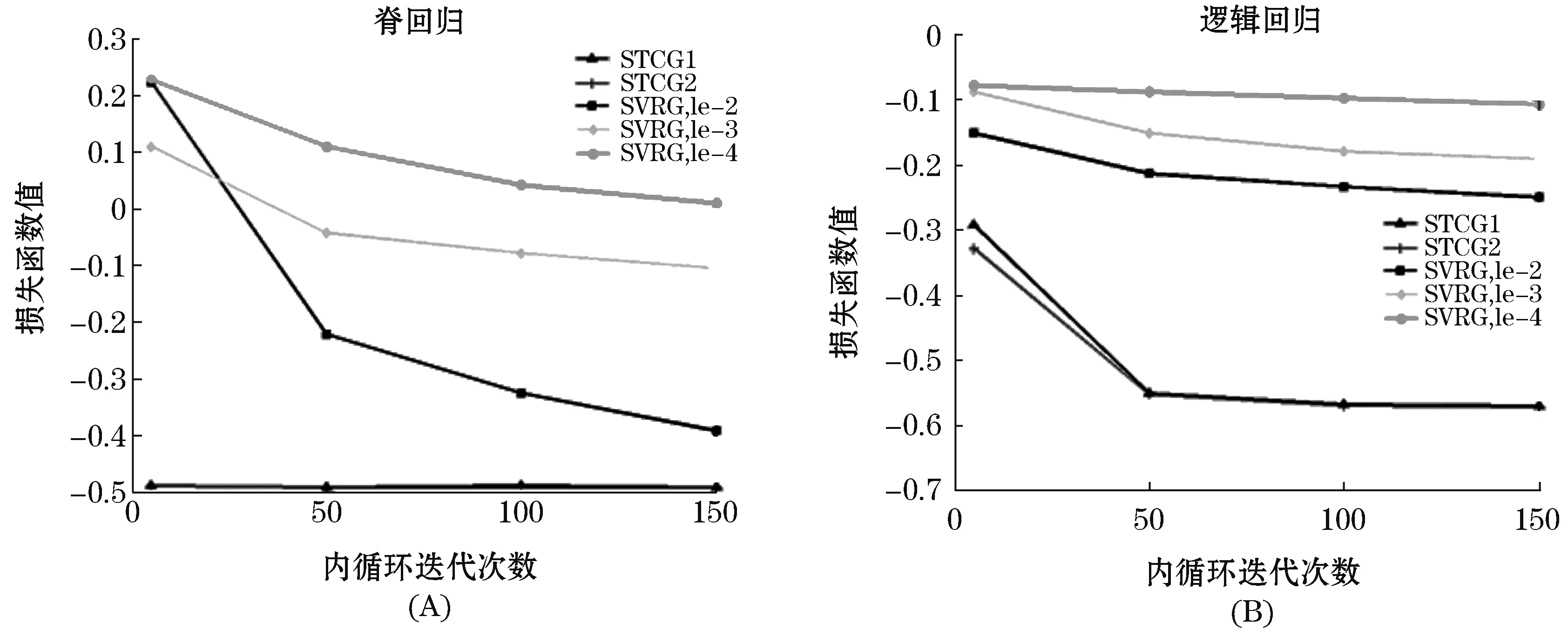
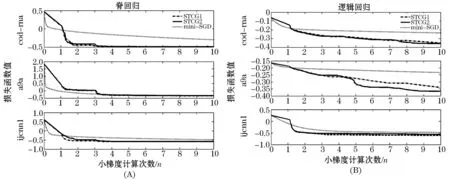
其中:0 共轭梯度方向pk为搜索方向,βk为共轭因子,不同的βk产生不同的共轭梯度方法.经典的共轭梯度法包括FR方法[11],PRP方法[12-13],HS方法[14]和DY方法[15].上述四种方法在收敛性质与数值表现方面存在较大差异,一般地,FR方法和DY方法在常用非精确线搜索条件下具有良好的收敛性质,但是它们的数值表现均不如PRP方法和HS方法.而PRP方法和HS方法对于一般目标函数,即使采取精确线搜索步长也无法保证全局收敛.近年来,为了建立具有良好收敛性质和高效数值结果的共轭梯度法,许多学者对以上经典共轭梯度法进行深入广泛研究,取得了一些较为理想的成果[16-17]. 三项共轭梯度法最早由Beale[18]作为一种再开始策略提出,其共轭梯度方向为: pk+1=-gk+1+βkpk+γkpt 其中:pt为再开始方向,参数γk定义为 但pk+1不一定是下降方向,在实践中该方法不是有效的[19-20]. 为了构造具有下降性质的共轭梯度方向,张等人[21-22]基于有限内存的BFGS法的三项形式提出了三项HS共轭梯度方向法和三项PRP共轭梯度法,其共轭方向分别为 (4) (5) 通过同样的构造方式,Moyi等人[23]考虑有限内存的SR1校正方法,提出了另一种三项共轭梯度方法3TCG-SR1,该方法中共轭方向满足充分下降条件.Arzuka等人[24]利用拟牛顿法Broyden族中的DFP方法,结合有限内存拟牛顿法对近似Hessian阵逆的更新,提出三项共轭梯度方法STCG,该方法中共轭方向满足充分下降条件和DL共轭条件. 由于共轭梯度法具有计算量小,存储量小等优点,人们开始研究随机共轭梯度下降法.Jin等人[25]提出了方差缩减的随机共轭梯度下降算法(CGVR),主要迭代格式为: pt=-gt+βtpt-1 ωt+1=ωt-αtgt 由于三项共轭梯度法在确定性优化问题中比两项共轭梯度法有更好的收敛性质和数值效果,因此本文考虑随机三项共轭梯度法,具体过程如算法1所示. 同样,梯度的近似是用小批量样本近似的,并且使用了x0处的随机梯度和它的全梯度对梯度近似进行了修正,这样可以减少一定计算量并得到方差较小的近似结果.同样,x0是周期性更新的点,每m次迭代更新一次.搜索方向为随机三项共轭梯度方向pt+1,为了有较好的计算效果,这里的pt+1选择的是式(4)和式(5),两种算法分别记为STCG1和STCG2.选取αt是通过非精确线搜索得到的,满足强Wolfe线搜索条件,与经典优化中不同,这里的强Wolfe条件为: fSk,t(xt+αtpt)≤fSk,t(xt)+c1αkfSk,t(xt)Tpt 其中:0 为了检验两种随机三项共轭梯度算法STCG1和STCG2的实际数值效果,我们将两种算法与SVRG,CGVR和mini-SGD进行比较,选取了下面两个常用于回归问题的损失函数极小化问题进行实验: 1)脊回归 2)逻辑回归 其中:xt∈Rd和yt∈{-1,+1}是第i个样本,λ>0是正则项参数.并且在预处理阶段,输入值X的每一个分量都被max-min压缩变为[-1,+1]范围内. 实验选取了表1中数据集,所有数据集均来自LIBSVM Data. 表1 数据集 实验均在PC机上完成,PC机的配置如下:Intel Core i5,8GB内存,Windows 10系统.程序用Matlab编写,运行环境为Matlab R2014a. 为了探究内循环迭代次数m对算法的影响,本文测试了外循环T=25时m分别为{5,50,100,150}的最终损失函数值.图2显示了在数据集cod-rna上STCG1,STCG2和SVRG在不同步长下随参数m的增加迭代完成后的损失函数值,横轴表示不同内循环迭代次数,纵轴表示迭代完成后的损失函数值在以10为底的对数下的值,图2(A)为在脊回归下的结果,图2(B)为在逻辑回归下的结果.我们发现,在设置适当的步长时,随着m的增加,SVRG在一定程度上降低了损失.STCG1和STCG2算法中损失函数值可以在仅包含5个内循环迭代的算法中快速下降,并且随着m值的增加,损失函数值差异不大.因此可以得出,STCG1和STCG2对参数m不敏感,且只需少量内循环即可快速收敛. 图2 内循环数对算法的影响 下面将内循环迭代次数m设为50,测试了STCG1,STCG2,SVRG和CGVR在相同外循环迭代次数下在3个大规模数据集上的损失函数值的下降情况.SVRG的步长选择10-2.图3显示了四种算法的收敛效果,横轴表示外循环迭代次数,纵轴表示损失函数值在以10为底的对数下的值.可以看出,STCG1和STCG2在脊回归和逻辑回归问题中仅需几次迭代即可达到极小值,收敛速度均比SVRG快.而且数值表现与CGVR表现相当,因此STCG1和STCG2是两种有效的算法. 图3 损失函数值随迭代次数的变化 除此之外,还将STCG1和STCG2与mini-SGD进行了比较,为了比较公平,我们比较了相同计算量下损失函数的值,这里用梯度的计算次数表示计算量.内循环迭代次数m=50,mini-SGD步长为10-2.结果如图4所示,横轴为小梯度计算次数/n,纵轴表示损失函数值在以10为底的对数下的值.可以观察到,总体来说,在相同计算量下,STCG1和STCG2的损失函数值的下降明显快于mini-SGD,说明两种新算法在收敛速度上是有优势的. 图4 损失函数值随梯度计算量的变化 本文提出了两种新的随机三项共轭梯度算法,分别为STCG1和STCG2,并与经典随机梯度下降类算法SVRG,mini-SGD和随机共梯度算法CGVR在求解两个回归问题时进行了数值实验的对比,结果说明STCG1和STCG2可以在几步迭代后达到极小值,收敛速度优于SVRG和mini-SGD.
2.2 随机三项共梯度算法


3 实验与分析



4 结 语
