前庭康复6-PSS并联机器人设计与ADAMS仿真

晏祖根，窦家明，刘玉斌，孙智慧，桑 华，康琪麟 (.哈尔滨商业大学 轻工学院，哈尔滨 5008; .哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 5000)

随着人口老龄化的加剧，越来越多的老年人出现身体运动功能障碍，其中前庭损伤是一个主要病因.医学研究表明，由于人体大脑的可塑性，通过重复的康复运动，可以提高运动功能障碍患者的协调性.传统的康复训练方法由人工或者借助简单器械带动患肢进行，医护人员的康复强度大、易受治疗师主观因素影响，限制了康复效果的提升.为了应对传统康复训练方法的不足，康复机器人应运而生.康复机器人将机器人技术和临床康复医学有机结合，可让病况差异、个体差异的患者主动参与而不是被动跟随，智能地适应精确化、自动化、智能化的康复训练[1]，实现人机之间协作、交互、共融的紧密耦合，进一步提升临床康复效果.

上肢康复机器人的研究相对较早，美国麻省理工的MIT-MANUS[2]、英国雷丁大学的GENTLE[3]、美国加州Palo Alto的MIME[4]、瑞士苏黎世联邦理工的ARMin[5]等为国外开发的不同形式的末端式上肢康复机器人，天津大学的李博超[6]、哈工大、上海交大等也开展了相关研究.在下肢康复机器人的研究方面, 最为典型的为瑞士苏黎世联邦理工的Lokomat[7]、美国麻省理工的Skywalker[8]、安徽工大的汪步云[9]、兰州理工的张淑珍[10]等相关研究.

目前，康复机器人的研究主要集中在上肢、下肢肌肉康复机构的研究方面，康复机器人平台的机构设计、人机交互、实验与评价等多个研究方面还存在不足，对于前庭功能损伤康复机器人的研究还较少开展.

1 前庭康复并联机器人工作原理

前庭是人体感受平衡状态变化的重要器官，由位于人耳内3个互相垂直的半规管和耳石器组成，半规管主要感受人体头部俯仰、偏转和滚动的运动信息，耳石器主要感受头部的空间位置变化和直线加速度运动信息.前庭将感受的人体平衡状态信息反馈给人体中枢系统，触发前庭觉.如果前庭功能障碍或者前庭损伤，患者会发生眩晕、平衡失调等问题，出现走路不稳、不自主偏向一侧的症状[11].

为实施个性化的平衡障碍康复训练，提出一种基于Stewart[12]机构的前庭康复6-PSS并联机器人机构，如图1所示.机器人由动平台、6条运动支链、基座等组成，每条运动支链由高性能的直线电机驱动，动平台的支撑连杆通过虎克铰分别与动平台、直线电机动子连接，机器人为6-PSS并联机器人.相比于液压缸、电动缸等驱动元件，直线电机具有更佳的动态性能.

图1 前庭康复6-PSS并联机器人系统Figure 1 Vestibular rehabilitation 6-PSS parallel robot system

通过控制基座上安装的直线电机的输出，可实时改变动平台的位置和姿态.人站立在机器人动平台上，实时感受运动平衡状态的变化，产生前庭觉.通过机器人多次的重复运动，提高前庭障碍患者的协调性，进行运动康复训练.

2 并联机构运动学建模

为实现康复并联机器人的优化设计、提高机器人控制性能[13-15]，将直线电机简化为移动副，虎克铰简化为球铰，建立并联机器人的机构简化模型，如图2所示.分别在机器人的基座、动平台上建立基坐标系和动坐标系，基坐标系{O-XYZ}原点O与基座几何中心重合，动坐标系{P-XYZ}原点P与动平台几何中心重合，基座与动平台的支撑连杆AiBi长度为L.

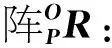
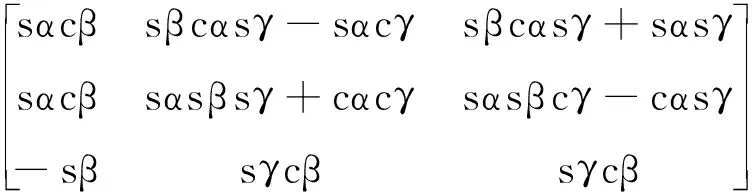
(1)

其中：c表示cos，s表示sin.

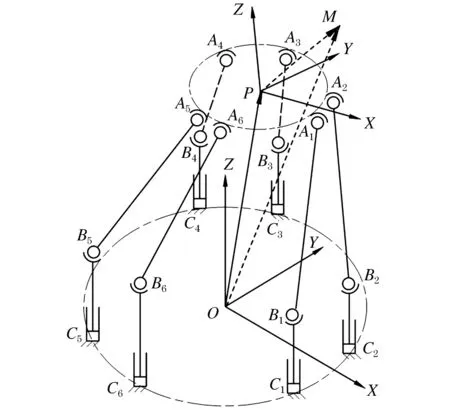
图2 6-PSS并联机构运动学模型Figure 2 Kinematics model of 6-PSS parallel mechanism

动平台上任意点M相对于动坐标系{P-XYZ}的位置矢量为pM，相对于基坐标系{O-XYZ}的位置矢量为OM，动平台坐标原点P相对于基坐标系{O-XYZ}坐标原点O的位置矢量为OP，则有：

(2)

3 并联机构运动学逆解

基座简化模型如图3所示，直线电机球铰点Bi在O-XY平面的投影点Ci位于半径为R的圆周上，Ci构成对称六边形的3条短边相等，短边C1C2长为2D.

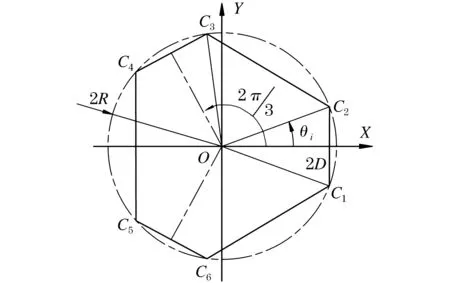
图3 基座简化模型Figure 3 Simplified base model

Ci点在基坐标系{O-XYZ}的位置为：

OCi=[RcosθiRsinθi0]

(3)

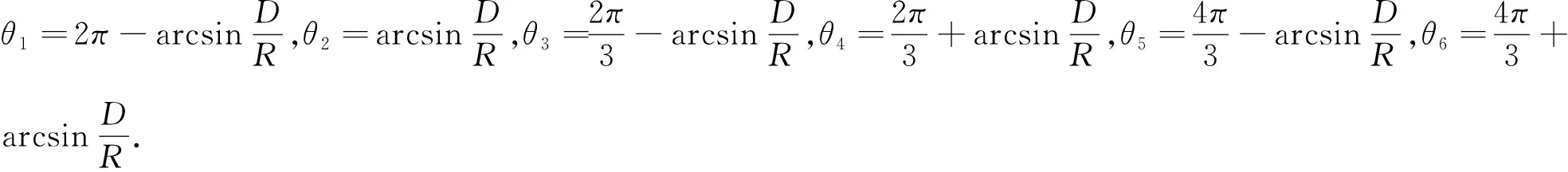
直线电机各球铰点Bi在基坐标系位置为：

OBi=[RcosθiRsinθizi]

(5)

其中：zi为对应直线电机动子移动距离.

动平台简化模型如图4所示，球铰点Ai位于P-XY平面半径为r的圆周上，Ai点构成对称六边形的3条短边相等，短边A1A2长为2d.

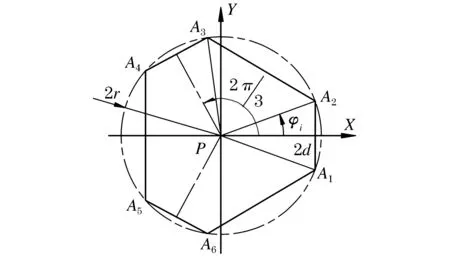
图4 动平台简化模型Figure 4 Simplified model of moving platform

Ai点在动坐标系{P-XYZ}位置为：

PAi=[rcosφirsinφi0]

(6)

结合式(2)、式(6)，可求得Ai点在基坐标系的位置为：

(8)

动平台运动过程中，支撑动平台的各支杆长度L保持不变：

|AiBi|=L

(9)

如已知并联机器人动平台任意时刻的位姿OP，将式(5)的OBi、式(8) 的OAi代入式(9)，可求取该时刻各直线电机动子移动距离，完成机器人运动学逆解的求解.

6-PSS并联机器人的运动学正解有歧义，很难直接求解，多应用牛顿迭代法、搜索法和神经网络等算法，进行快速的数值求解.

4 并联机构拉格朗日动力学分析

并联机器人具有封闭环结构及运动学约束等内在特性，建立其动力学模型非常复杂，常采用拉格朗日法(Lagrange) 、牛顿-欧拉法(Newton-Euler)、凯恩法(Kane)、虚功法等方法，分析并联机器人的动力学特性.

相比于其他方法，拉格朗日法在求解过程中，可避免对各执行构件速度、加速度的求解，具有运算简单、计算量小的优点，更能满足实时控制的需求.本文利用拉格朗日动力学方法分析并联机器人的动力学特性.

机器人的拉格朗日函数L为系统的动能E与势能U之差，即：

(10)

其中：mp为动平台质量，mD为直线电机动子质量，mL为支杆质量(含两端虎克铰)，JL为支杆绕质心的转动惯量，vLi、ωLi为支杆的运动速度与旋转速度，JPx、JPy、JPz为动平台的转动惯量，vPy、vPz、ωPx、ωPy、ωPz为动平台的运动速度与旋转速度，vDi为直线电机运动速度，zLi为直线电机动子移动距离.

式(10)中支杆的运动速度vLi、旋转速度ωLi可通过图5的单运动支链机构简图求得.

动平台上球铰点Ai速度为：

vAi=v+ω×Ri

(11)

其中：Ri=RPAi，PAi为Ai点在动坐标系的位置矢量，动平台速度v=(vpx,vpy,vpz)，角速度ω=(ωpx,ωpy,ωpz).

支杆两端上、下球铰速度关系：

vBi·Li=vAi·Li

(12)

其中：Li为向量AiBi在基坐标系中的位置矢量，vBi为球铰Bi速度.

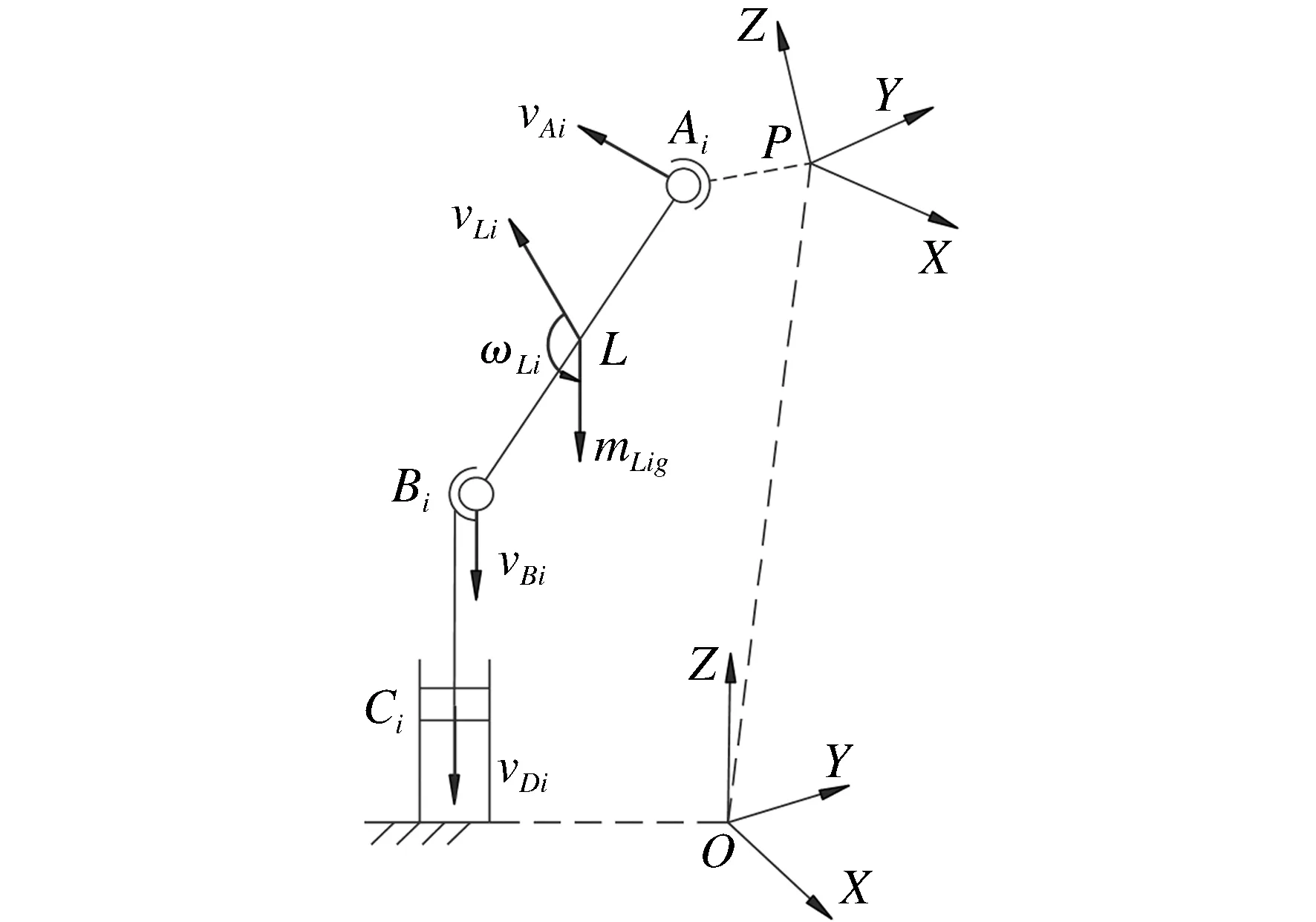
图5 单运动支链机构简图Figure 5 Single motion branched chain diagram

将式(12)代入(11)中得：

(13)

球铰Bi的速度可以简化为[0,0,vBi]，则直线电机动子球铰Bi的速度为

(14)

(15)

动平台球铰速度也可表示为：

vAi=vBi+ωLi×Li

(16)

可求得支杆AiBi的质心运动速度vLi与绕质心旋转速度ωLi：

vLi=vBi+ωLi×Si

(17)

(18)

其中：Si为Bi到支杆质心的矢量在基坐标系中的螺旋表示.

将机器人的拉格朗日函数L代入拉格朗日动力学方程：

(19)

由式(19)可求得：

(20)

直线电机动子速度与动平台速度之间存在如下映射关系：

[vD1vD2vD3vD4vD5vD6]T=J×[vPxvPyvPzωPxωPyωPz]T

(21)

式(20)表示作用在动平台上的广义力分力，根据虚功原理，可求得直线电机的驱动力：

τ=[τ1τ3τ3τ4τ5τ6]

(22)

τ=JT·F

(23)

通过上述各式，当给定该动平台的位置、速度、加速度，可求出运平台广义力和直线电机的驱动力.

5 ADAMS虚拟样机仿真

5.1 搭建虚拟样机

结合康复医院的前庭障碍患者康复治疗经验，确定前庭康复机器人的设计要求：

1)动平台实现6自由度运动；

2)负载：100 kg；

3)运动范围：3个方向平移量：±30 mm，3个方向旋转量：±4 °；

4)最大加速度： 1 m/s2.

根据前庭康复机器人的设计要求，选用台达LMS67型直线电机，初步确定机器人的主要机构尺寸：动平台直径650 mm，短边长160 mm，基座直径1 200 mm，短边长280 mm，支杆长度705 mm.

基于Solidworks，建立机器人三维模型，并导入ADAMS，建立机器人的ADAMS虚拟样机模型.给虚拟样机添加约束副和驱动：在每条运动支链的球铰点Ai、Bi处添加球副约束，直线电机添加移动副，动平台上施加120 kg的负载.

5.2 动平台运动规律

各运动支链直线电机的驱动函数非常复杂且难以确定.进行运动学仿真时，先从运动学逆解出发，看其是否能够达到要求的运动状态，并查看是否有干涉现象发生.借鉴相关文献，确定动平台中心点的运动规律函数：

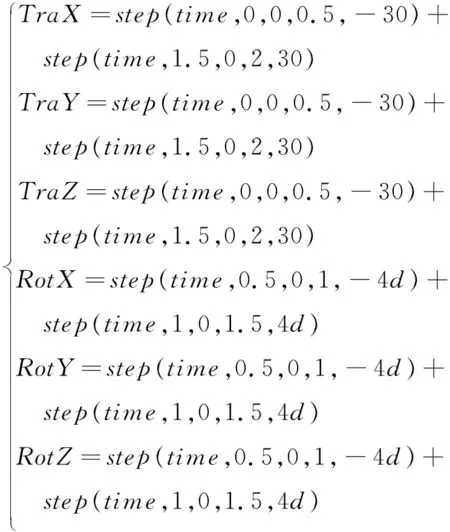
(24)

上式的运动规律，在0～0.5 s运动过程中，动平台沿X、Y、Z轴分别移动30 mm；0.5～1 s间，绕X、Y、Z轴逆时针旋转4°；1～1.5 s间，绕X、Y、Z轴以相同速度顺时针旋转4°；1.5～2 s间，再沿X、Y、Z反向移动30 mm，回到初始位置.

5.3 动平台运动仿真

将式(24)所示的动平台运动规律函数导入机器人的ADAMS虚拟样机，计算出动平台中心点位移、速度、加速度的合成曲线，如图6所示，位移曲线值是动平台中心点相对于基坐标系原点的合成位移值.动平台的角加速度与角加速度如图7所示.

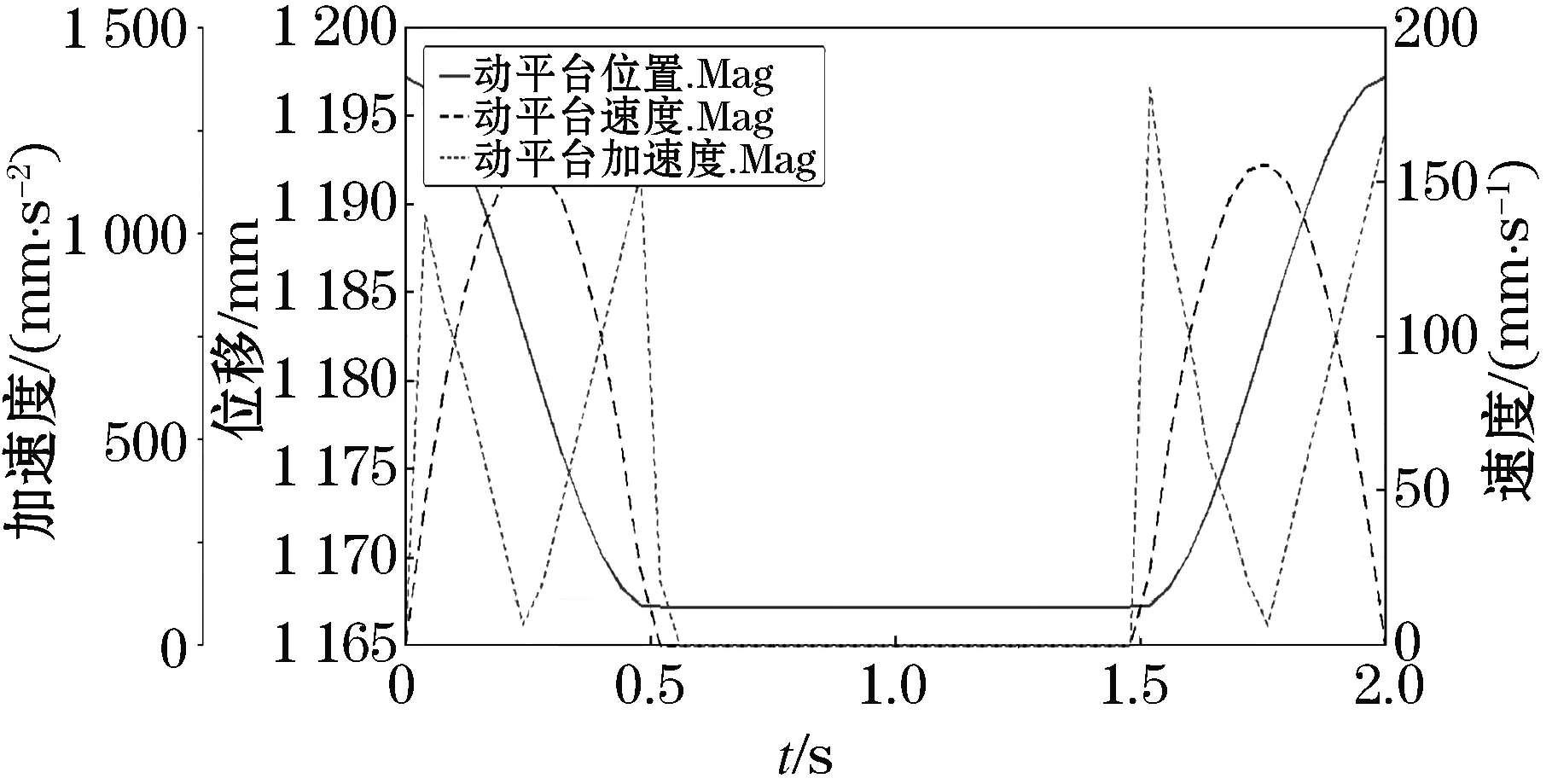
图6 动平台中心点的位移、速度、加速度曲线Figure 6 Displacement, velocity and acceleration curves

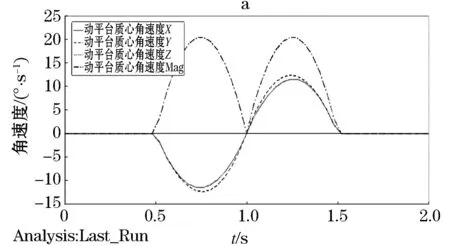
图7 动平台的角速度、角加速度曲线Figure 7 Angular velocity and angular acceleration curves

由图7可看出，动平台在0～0.5 s间呈下降状态，最大加速度为1.2 m/s2，最大角速度20 °/s.0.5～1.5 s间保持不动，动平台绕X、Y、Z轴旋转，线速度与加速度都为0.在1.5～2 s呈现线性回复状态，最大加速度为1.2 m/s2，回复到初始位置.

各驱动直线电机动子的位移曲线如图8所示.0～0.5 s运动过程中，各电机动子线性下降.1.5～2 s 间，电机动子线性下上升.0.5～1 s运动过程中，动平台仅绕X、Y、Z轴逆时针旋转，三个电机动子上升，另三个电机动子下降.1～1.5 s间，动平台绕X、Y、Z轴顺时针旋转，电机动子移动方向与前相反.

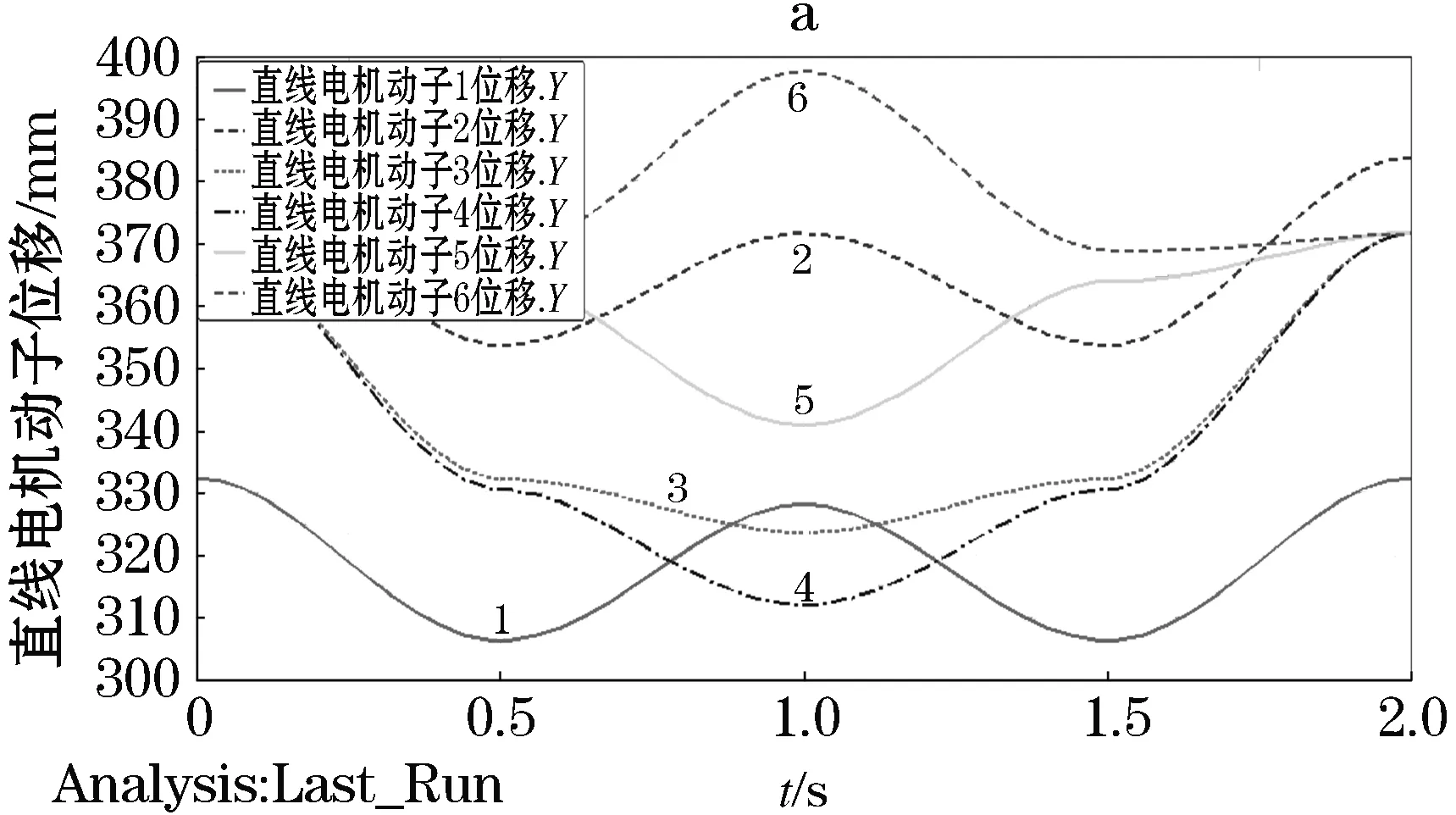
图8 直线电机动子位移曲线Figure 8 Linear displacement curve of electric motor

利用虚拟样机进行并联机构逆解计算，生成各直线电机的驱动样条函数，如图9所示.实际应用时，可调用所生成的驱动样条函数，融合轨迹规划、力矩控制、动力学控制等因素，实现康复并联机器人的实时控制.

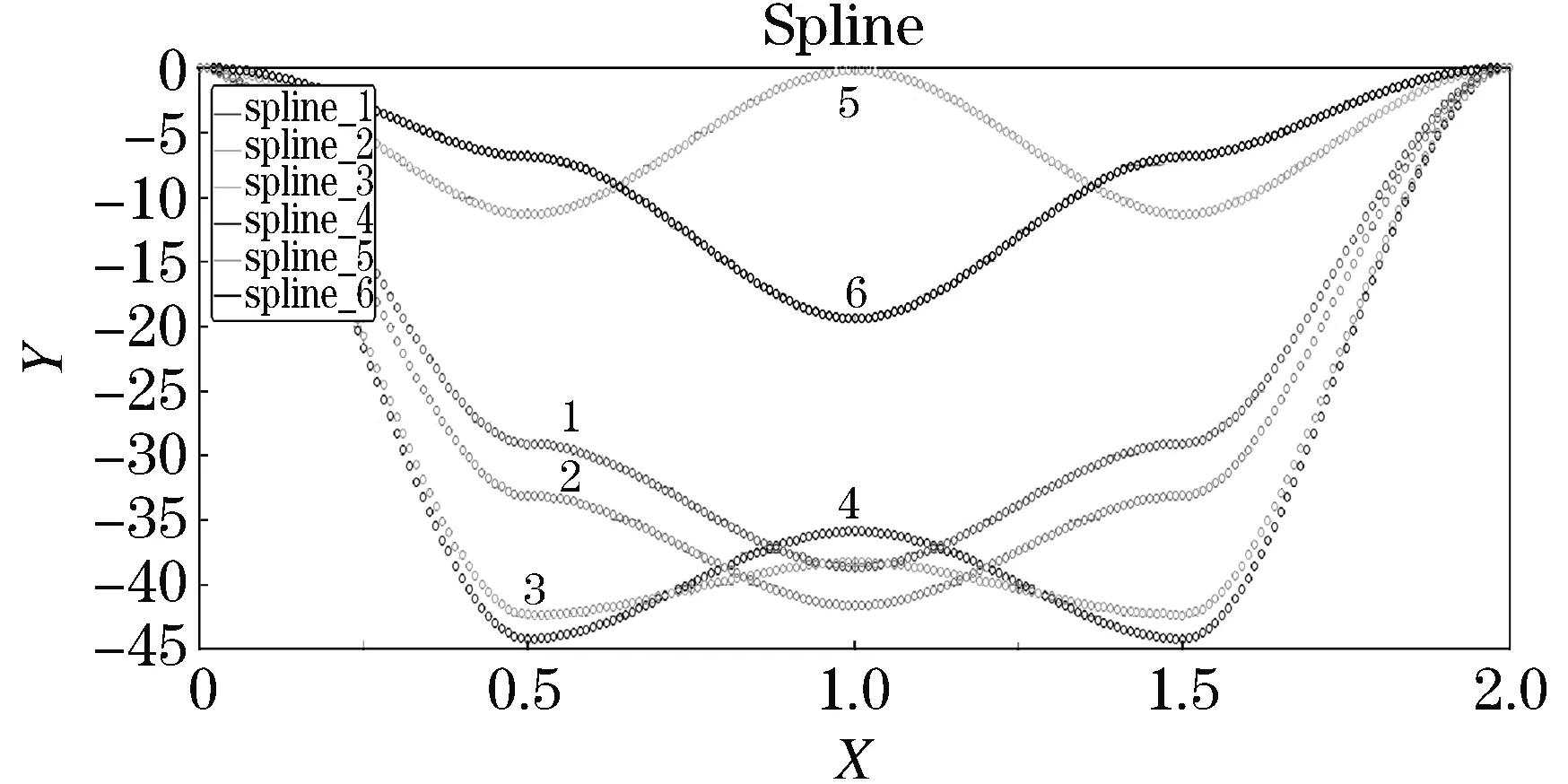
图9 驱动样条函数Figure 9 Drive the spline function

直线电机驱动力变化曲线如图10所示.在动平台下降到最低位置时，动平台突然加入转动；在从最低位置开始上升时，转动开始退出.转动的突然加入与退出，会改变并联机构的动力特性参数，使动平台出现剧烈波动.这种动平台的剧烈波动，可用于刺激动平台上前庭障碍患者的前庭觉，以利于患者的前庭康复.

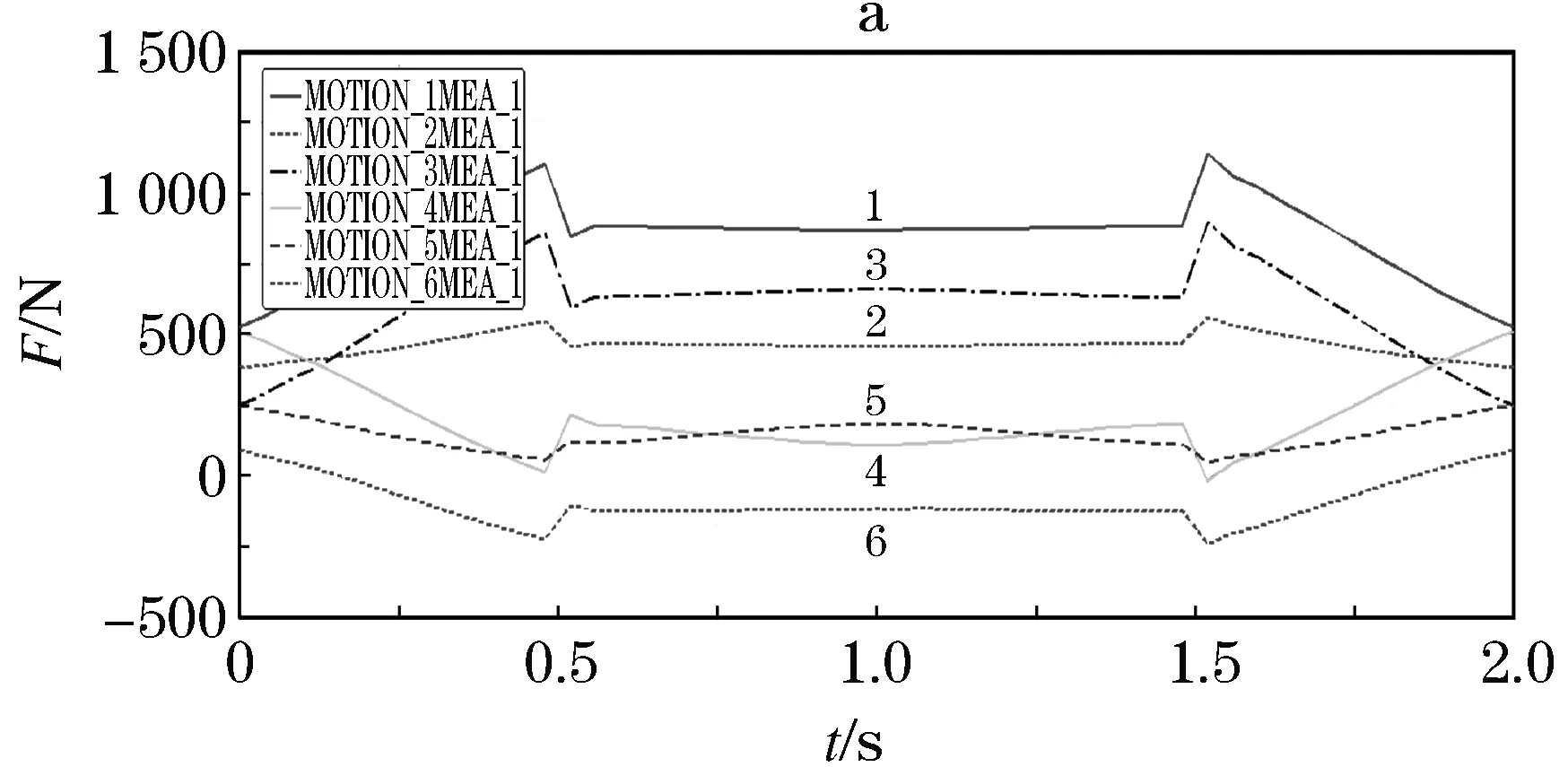
图10 直线电机驱动力变化曲线Figure 10 Driving force curve of linear motor

6 结 语

为帮助前庭障碍患者进行科学有效的康复训练，设计了一种基于直线电机驱动的前庭康复6-PSS并联机器人，建立了机器人运动学模型和拉格朗日方程动力学模型，得出了机器人运动学逆解.基于ADAMS，建立机器人的虚拟样机并仿真，仿真结果表明，机器人动平台最大加速度为1.2 m/s2，可有效刺激患者的前庭觉，进行前庭障碍患者康复训练.后续要研发前庭康复机器人样机，开展患者的康复训练实验研究.