可视化视角下的数学解题教学：取势、明道、优术*——以高三二轮微专题复习课“与导数有关的函数零点问题”为例

张志勇 (江苏省常州市第五中学 213001)

张加红 (江苏省常州市田家炳高级中学 213001)

解题可以帮助学生深刻理解数学概念、掌握数学方法进而锤炼数学思维，正如波利亚所言，“掌握数学就意味着学会解题”.解题教学无疑是数学教学的重点，对于高三数学复习而言，更可谓是主旋律．如何开展解题教学？不能只有“数”(计算推理)而不见“形”(想象直观)，不能只有解题方法的简单堆积而没有对解题策略的思考，不能只有“怎么解”的具体操作而没有“为什么这样解”的不断追问．有鉴于章建跃博士提出的数学教育要“取势、明道、优术”[1]，我们以为，数学解题也需要“取势、明道、优术”；在可视化技术的支持下，通过直观想象指引解题方向(取势)、深度挖掘明晰本质属性(明道)，达成模型构建优化解题方案(优术)的解题教学目标．在此过程中，不仅有解题思路的过程展示，解题策略的形成解构，更有解题观念的实质突破和“原来如此”的美妙感悟．本文谨以一节高三微专题复习课“与导数有关的函数零点问题”为例，与读者分享可视化视角下的数学解题教学．

1 基本情况

1.1 授课对象

学生来自四星级高中普通班，数学基础一般，已经历过高三一轮复习，掌握基本的数学运算和简单的逻辑推理，如求导、利用导数判断函数单调性、判断零点的个数等；有一定的阅读表达能力，对数形结合的解题思路较熟悉，能判断函数变化趋势进而讨论渐近线的存在性，并能结合单调性和可能有的渐近线绘制函数示意图；基本掌握GeoGebra的常见操作要领，能简单应用软件开展数学探究活动．

1.2 内容分析

纵观近几年的高考、模考试题，与导数有关的函数零点问题是函数压轴题中的常客，此类问题将函数、不等式、方程等知识综合在一起，能有效区分学生数学能力的水平差异，故而广受命题者青睐．从知识层面看，导数和零点存在性定理是解决这类问题必不可少的工具，应用导数判断函数的单调性没有多少障碍，难点在于零点存在性定理的应用，而此中关键在于“找点”，即构造异号的函数值，这是颇具技巧又很有计算难度的一步．如何突破运算的难点？“数形结合”无疑是一可行路径.绘制函数图象，借助图象能直观帮助学生认识结果、明辨解题方向；进一步地，图象更可以揭示真相，最终帮助学生优化解题方法、形成解题模式．

据此，本节专题复习课拟采用的教学策略为：一是重视数形结合，借助单调性和变化趋势绘制函数图象，以图象直观来判定参数范围及取点方向；与此同时，借助GeoGebra开展数学实验，让学生在动态观察中把握数学本质.二是重视问题引导，在思维“关节点”与“关键点”处驻足停留，对于为什么这样“取点”、怎样放缩等问题，通过问题串的方式不断地追问，以引导、帮助学生认识数学本质并掌握数学方法．

1.3 教学目标

(1)经历完整的数学解题方法的探求过程，感悟数形结合的解题价值，在取势、明道、优术中让自己的数学理解和思考从模糊走向深刻．

(2)能在准确把握函数特征(单调性、渐近线等)的基础上绘制较复杂的函数图象，结合图象判断零点的存在、参数的范围；把握零点存在定理的应用要求，采用按图索骥、函数放缩、结构化简等不同方法“找点”证明零点的存在．

教学重难点：函数放缩与“找点”．

2 教学过程

2.1 归类辨析，聚焦问题

问题1(改编自2020年苏锡常镇一模13题)若ax=x2在(1,+∞)上有两解m,n，求a的取值范围．

图1

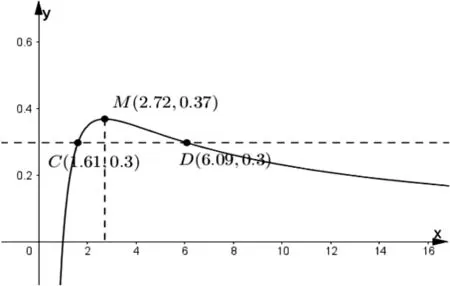
图2

2.2 按图索骥，初解取势

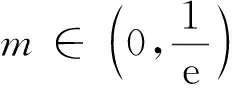
2.3 函数放缩，再解明道

根据图象趋势“找点”，虽然可以解决问题，但这样的尝试理由并不显然，有必要进一步探究以明了个中奥妙．我们将其中的关键不等式换元处理后可得到如下简化的不等式：

图3

图4

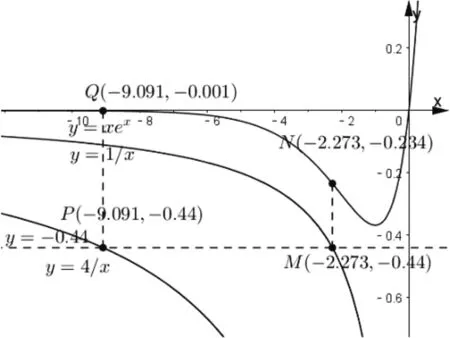
图5

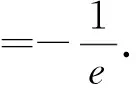
说明本例中，关键“点”在直线上方，因此构造的函数图象在原函数下方．

2.4 结构化简，三解优术

例1(2019年南京三模试题19改编)关于x的方程lnx+1=bx2有两个不等的实数根，求b的取值范围．

图6

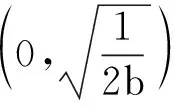
练习：(1)已知函数f(x)=ax2-x-lnx有两个零点，求实数a的取值范围．

(2)已知函数f(x)=mex-(x-1)2有三个零点，求实数m的取值范围．

2.5 梳理总结，形成范式

结合课堂教学中涉及的案例，梳理问题解决过程，可总结出下列要点：

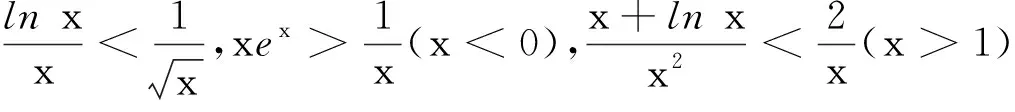
(2)放缩方法有章可循．放缩的目标是将不易解的不等式转化为易解的不等式，通常做法是将指对数函数化为多项式函数．由两个简单基本不等式lnxx出发，可演绎出不简单的放缩形式；

(3)放缩千万,趋势为要．不同函数的“变化趋势”不同，放缩不能改变函数整体的相对变化趋势(极限一致)，原函数图象的变化趋势需要结合导数整体辨析．

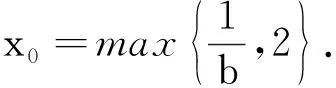
简而言之，就是“零点判定有讲究，图象观察辨趋势；函数变换是根本，放缩有度分主次”．

3 回顾与反思

因为运算难度大，面对与导数有关的函数零点问题，多数学生望而生畏、止步不前．本节课在“取势、明道、优术”的思路指引下，三次求解零点问题，形成三种不同解法(按图索骥法、函数放缩法、结构化简法)，不同水平层次的学生可选择不同的解法．更为重要的是，可以改善学生拿笔就算的解题习惯，回归数学直观探究先行，促使计算推理也能返璞归真，在帮助学生掌握一类题的解法过程中让学生学会数学地思维．

3.1 数学解题中的取势明道优术

将“取势、明道、优术”用于数学教育中，章建跃博士是强调教育要明确方向、把握规律、办事有方[1]；用于解题中，则是指直观想象指引解题方向(取势)、深度挖掘明晰本质属性、模型构建优化解题方案(优术)．具体而言，“术”多指抽象的数学方法、繁杂的计算技巧，如本例中的“取点”.如果只是为术而术、停留于“知其然”层面，一方面会因难以理解而不为学生所接受和优化，另一方面也会因“见木不见林”而难以生成和旁通．因此解题不应只囿于解题技巧的获得，而应走向“知其所以然”，让学生理解其中的函数放缩．明道就需要追本溯源，首先得聚焦关键环节、分析问题特征，然后才是丰富表征手段、找寻联系通道，在抽象的“数”之间架设具象的“形”作为桥梁，无疑是帮助学生问道明理的重要情境．解题也需要看清方向，方向不对则多做多错，而“形”正可以揭示“大势所趋”，让最终结果在解题前就“观念性地存在着”，而不再是摸着石头过河．事实上，当我们绘制出图2所示的函数图象后，问题2的结果已经水落石出，跟进的只是数学的解释和证明罢了．解题中的取势明道优术，告诉我们的是不仅要埋头赶路，更要抬头看路；优术的前提在于明道，取势方能明道．

3.2 数形结合与深度学习

提及数形结合，耳熟能详的是华罗庚先生说过的“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．虽然数形结合是重要的数学思想方法，然而解题时(特别是主观题)多数时候却有“数”无“形”．究其原因，一方面当然有评价更重视严谨的计算推理的缘故，另一方面也因为对数学对象的本质特征把握不全面，难以绘制准确的图象，如图2中f(x)的图象刻画离不开对单调性、最值、渐近线的考量．“形”可意会取势，“数”为优术言传，我们这儿强调“形”的价值不只是为了得到结果，更重要的是为“数”的推理提供方向直观，如由图2发现找点方向(足够大、在直线下方、与变量有关)，由图5思考函数放缩(趋势一致，放缩有度)，“形”的展示不仅有想象直观，更有深透的理解、深入的思维和深切的体验．

3.3 GeoGebra与数学可视化

数学可视化就是“看见不可见”，即将抽象的数学对象用可看见的表征形式清楚直白地呈现出来，从而得到一个形象、直观、整体的认识和理解．作为一款数学学科软件，GeoGebra实现了“形”(几何)与“数”(代数)的完美融合，可以将抽象的数学知识直观化，使数学的关联性变得可见甚至可操作，从而帮助学习者洞悉数学本质．如图6中“作差”与“分参”两种思路的比较呈现，图4中切线放缩的动态呈现等．GeoGebra带给我们的不仅是更加方便快捷的数学，更是理想的深度学习平台和深度教学工具．

数学解题，不仅是解决问题，更重要的是观点的提高和思维的启迪．“形”可意会取势，“数”为优术言传，“取势、明道、优术”的思路为当下数学解题教学提供了一个全新的思路，而可视化恰可让学生将更多的精力集中在高层次的数学思考和问题解决上．