咬定目标不放松 立根原在模块中*

陆一烽 张岭芝 (江苏省无锡市青山高级中学 214036)

核心素养为纲的理念如何转化为学校教育教学的实际行动，发展学生的核心素养，教学该如何做？[1]数学运算是重要的数学核心素养，《普通高中数学课程标准(2017年版)》指出：数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等.[2]笔者在高三教学实践中发现，高三学生在数学运算方面不同程度地存在着以下问题:有的不会根据题目条件选择合理的运算思路，有的不能在具体的题境中明确合适的运算对象.运算来源于情境，本文以高三解析几何复习中一类题型为例，从模块化设计的角度谈谈在培养学生数学运算这一核心素养上的一些尝试.

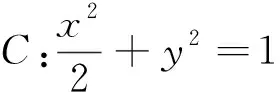
本题考查直线的方程、直线与椭圆的位置关系,考查数学运算等数学核心素养.笔者从学生的解答发现，第一问解答较好，但是第二问情况差了很多,很多学生没有对直线进行分类讨论,也不知道如何在直线l与x轴不重合不垂直的情况下与椭圆联立来证明∠OMA=∠OMB.这个问题在教师眼里看似简单，但是在刚进入高三的学生眼里却可能是陌生的.对于这一点，笔者很快在讲评课中得到了验证.有学生回答：这是一个几何结论,通过角平分线定理来证明两角相等.笔者表扬了学生扎实的平面几何知识,列出了角平分线定理的式子,并引导学生发现后面的计算量不小(运算思路).还有什么方法?考虑到在l与x轴不重合不垂直的情境中,两角相等有没有什么等价的代数形式？经过引导，让学生考虑斜率和倾斜角的关系，大部分学生终于发现只要证明kMA+kMB=0(运算对象).最后留给学生课后思考:如果以后要证明α=2β,应该怎么证呢?

问题中,学生的困惑主要体现在如何证明∠OMA=∠OMB.怎样在教学中帮助学生选择合理的运算思路，明确合适的运算对象呢？笔者想到了模块化.

生活中,模块化设计已经成为很多产品的设计主流，所谓模块化设计就是将产品分成几个部分，也就是几个模块，通过不同模块的排列组合可以形成不同的产品.模块化设计效率高，执行快.就数学运算而言,那些经常使用，根据题设条件呈现的相应数学知识,都可以归为基础模块.常见的基础模块有：设点或直线的方程、点在线(或曲线)上、韦达定理、三点共线、斜率之和(积)、向量的线性表示等.而根据题目目标建立目标的等价性转化，如将α=2β转化为证明tanα=tan 2β，或者根据求解目标的特征建立基础模块之间的新组合来创造性地解决问题,则属于创意模块.

1 基础模块反映了数学运算应该渗透对通性通法的掌握

解析几何的基本思想方法就是把几何问题转化为代数问题，问题的形式有新有旧，但其解决离不开这一基本思想.所以要鼓励学生把显性或者隐性的几何条件转化成代数条件，形成基础模块.像上述问题,如果学生能够有意识地假设出过点F的直线方程和点A,B的坐标,并能够联立直线与椭圆的方程,形成韦达定理,就会逐步接近设计出kMA+kMB=0这一运算对象.下面再举例说明.

例1(2019·北京理第18题第二问)已知抛物线C：x2=-4y，设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=-1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点．

分析 从逻辑推理的角度,要证明以AB为直径的圆经过y轴上的两个定点，就要先求出圆的方程，而要求圆的方程就要求出A,B两点的坐标，这就是整个题目的运算程序.所以设M,N坐标，直线l:y=kx-1，求出A,B坐标，这些都是基础模块，在圆心和半径的化简过程中还用到了韦达定理这一常用基础模块.教师在教学实践中应该指导学生不要匆匆做题，而要耐心审题、读题，逐一分析表达，让学生感受运算程序的完整性．

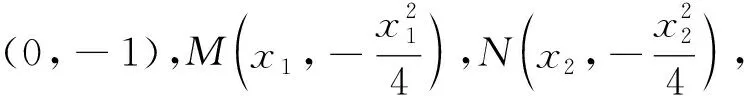
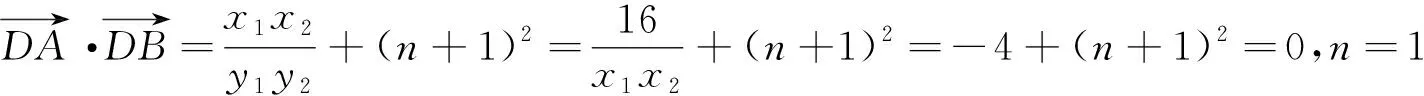
2 创意模块充分体现了数学运算承担着从已知到未知、化难为易的重任

除了建立目标的等价性转化是创意模块,根据求解目标的代数特征,执果索因,建立基础模块之间的新组合来解决问题,也是创意模块.在一些数学运算中，运算对象并不明显，运算思路并不容易.

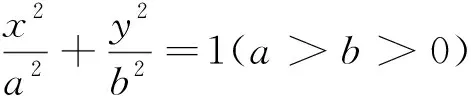
图1

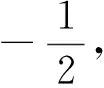
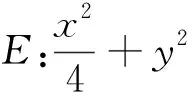
图2

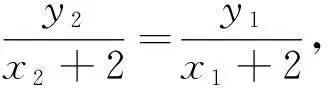
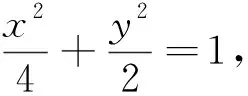
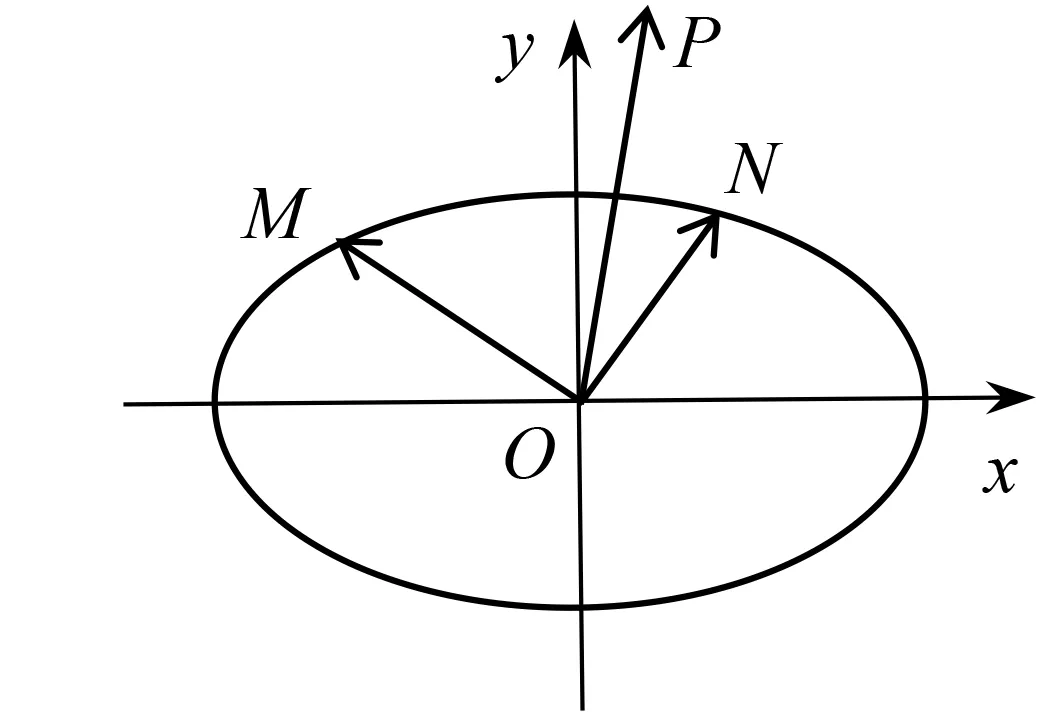
图3

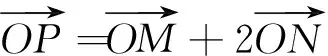
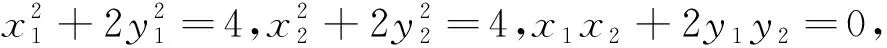
综上,模块化设计首先要把源头和底层的东西搞清楚.在解析几何这一类问题中，教师要在教学中鼓励学生把几何条件转化为代数语言,形成基础模块，再通过代数式的运算来解决问题.没有基础就没有创造.创意模块的设计,需要追根溯源，善于发现几何与代数问题间的等价性转换,运用常数代换、部分替换、配凑等运算技能，分解目标式，巧妙组装基础模块，打通障碍，直至得到结果，这充分体现了数学运算从已知到未知、化繁为简、化难为易的功能.