铸铁机链轮传动部件动态特性分析①

张良 李云祥 韩芩

（1：江汉大学智能制造学院 湖北武汉430056；2：陕西钢铁集团汉中钢铁公司 陕西汉中724207；3：武汉晴川学院机械与电气工程学院 湖北武汉430204）

1 前言

在钢铁企业中，当炼铁生产的铁水多于炼钢生产能力或者炼钢设备检修时，需要铸铁机将铁水铸造成铁块，供后期使用。因此，铸铁机是铁钢产能平衡的关键设备。铸铁机一般由驱动装置、链传动、铸铁模、喷淋和喷浆等部件组成，其中链传动部件包含主动链轮、从动链轮和链条等部件。链条与链轮组成具有一定倾角的循环链传动，其倾斜角度一般为8°～10°。链条的松、紧边由支撑托辊支撑，两端分别与主、从动链轮啮合。主动链轮与驱动装置连接，安装在倾斜角度顶部，基础为钢平台或混凝土平台。从动链轮与张紧装置安装在倾斜角度底部的基础上。

对于铸铁机的研究主要集中在部件结构或工艺布置上。付志林［1-2］从链条的结构特点进行了研究，防止链条松弛。王伊宁［3］对链条在运行过程中出现跑偏问题进行了分析。阮建波［4］从工艺布置上总结了铸铁机在设计过程中需要注意的问题。以往的研究工作，缺少对链传动的链轮和链条的动态特性进行研究，进而从振动特性上去分析链传动出现的问题。在本文中，以主动链轮和链条作为研究对象，分析了啮合过程，并对其进行了模态分析以及谐响应分析，得到了固有频率和振型，以及受外部激励时产生最大振幅的频率范围。根据理论分析，实际生产中可以采取相应措施，避免铸铁机在运行过程中链条振动过大，出现打滑或跑偏等问题。

2 链传动

2.1 结构特点

铸铁机链条是由若干个直边链节通过实心销轴连接而成，一个链节的长度一般为500mm～600mm。链轮为双拼星型链轮，链齿上设置开口凹槽。运行时，链节的销轴与链轮上的开口凹槽相互接触啮合，由于链条的多边形效应，使链轮带着链条转动。

2.2 啮合过程

链轮与驱动装置连接，绕自身轴心旋转，带动链节以平移的方式运动，进而实现链条绕链轮轴心线转动。链轮做旋转运动，首先带动第一个链节的销轴进入链轮开口凹槽中，当销轴滑移一段距离后，其轴心与凹槽底部圆弧段圆心重合时，完成第一个链节与链轮的啮合过程。链轮继续转动时，第二个链节销轴进入链轮开口凹槽中，当销轴轴心最终与凹槽底部圆弧段圆心重合时，完成第二个链节与链轮的啮合过程。当第三个链节的销轴进入链轮的开口槽内时，同样轴心与圆心重合时，第三个链节与链轮啮合过程完成。依次以此方式，完成链条与链轮啮合过程。链条的节距与链轮节距相等，保证啮合过程的平稳，啮合过程见图1所示。

图1 链传动的啮合过程

3 模态分析

3.1 模态分析理论

模态分析理论是最近几十年在机械阻抗和导纳理论的基础上发展起来的，涉及到振动力学、信号处理、数据分析等理论，现在广泛应用于机械结构动力学分析中［5-9］。

实际工程中许多旋转机械的振动问题多为多自由度系统，如车床主轴、减速器齿轮、链传动链轮等，多自由系统利用矩阵分析方法，N自由度线性定常系统的运动微分方程为：

式中：M、C、K—系统的质量、阻尼和刚度矩阵（均为N×N阶矩阵）；

X、F—系统各点位置上的位移响应和激励力向量。

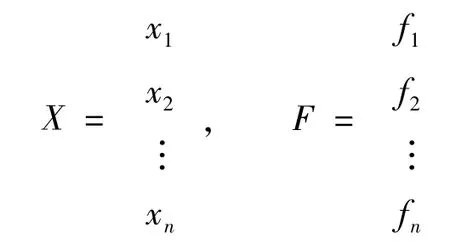
对（1）式两边进行拉氏变换，得到：

式中的拉氏因子：

s＝σ＋jτ

s*＝σ-jτ

经过转化得到：

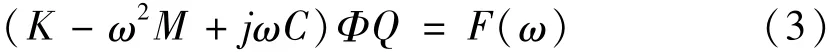
考虑铸铁机链传动阻尼因素，系统阻尼满足下列条件：

式中α，β为比例系数。对其进行解耦变换：

通常情况下［Cr］′并不是对角阵，这使得求解变得非常复杂，在工程中对其进行忽略非对角元素的近似处理，简化为对角阵［Cr］，称为模态阻尼。

由此可将系统的运动方程表示为：

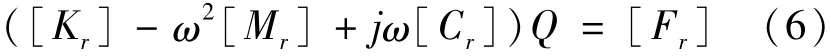
即对第r阶模态有：

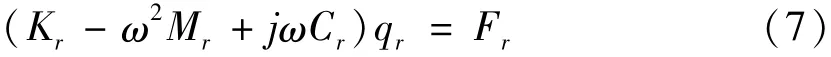
其中Fr＝φrTF（ω），其中ω为系统的固有频率。

3.2 有限元模型

在三维软件中建立链轮与链条装配体三维模型，处理倒角、倒圆等小几何特征，将模型导入ANSYSworkbench中，进行网格划分，局部几何特征细化网格，建立有限元模型，见图2所示。

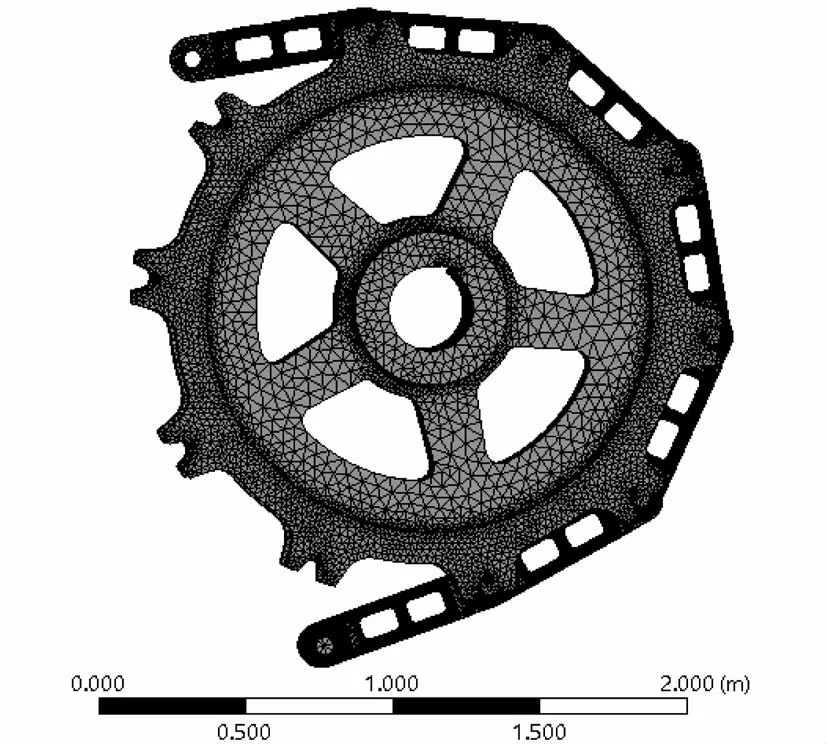
图2 有限元模型

3.3 约束设置

链轮和链条模态分析的目的是得到其固有频率和相应振型，因此，不需设置外部载荷，只需对其进行自由度的约束。链轮内孔圆柱面与主轴采取过盈配合，其自由度受限制，即约束。

模态提取有很多种方法，对链轮和链条进行模态分析采用Lanczos法，提取前5阶的模态固有频率以及对应振型。

3.4 后处理

经过对链轮和链条的模态分析，得到其前5阶固有频率和振型，见图3所示。

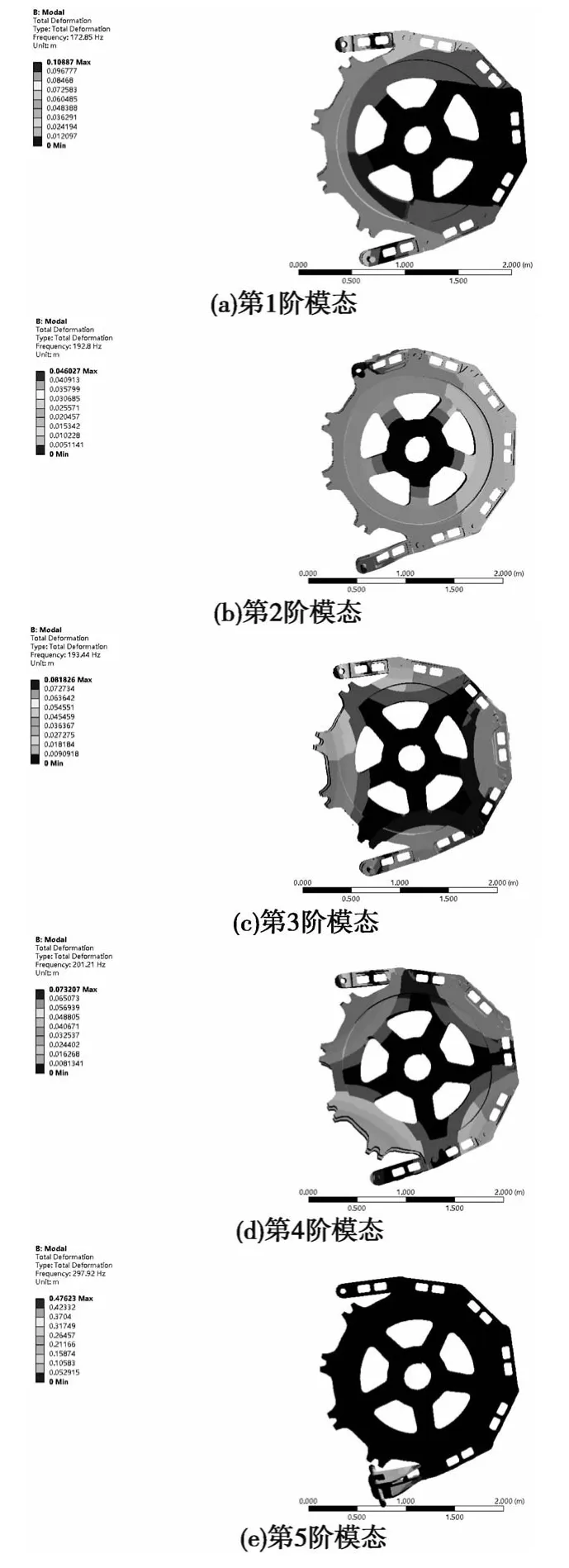
图3 模态振型

第1阶模态固有频率为172.85Hz，振型主要是绕链轮轴心变形，还未完全与链轮啮合的链节出现弯曲变形。第2阶模态固有频率为192.8Hz，振型仍然主要为绕链轮轴心变形，并在平面内发生弯曲变形。第3阶模态固有频率为193.44Hz，在平面内的振型主要为弯曲和扭转组合变形。第4阶模态固有频率为201.21Hz，振型主要为平面弯曲和扭转变形。第5阶模态固有频率为297.92Hz，振型主要是链节发生弯曲形。

4 谐响应分析

4.1 谐响应理论

谐响应理论是以模态理论为基础，经过对位移和外部载荷的复变转化，得到谐响应的分析动力学方程［10］。

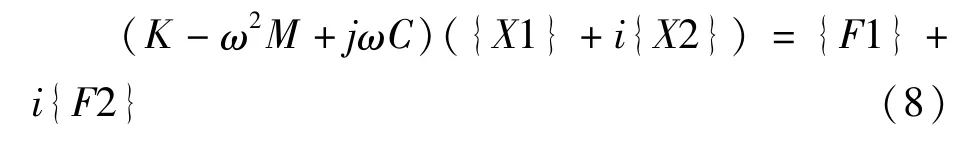
有限元分析软件ANSYSworkbench谐响应分析方法有模态叠加法和完全法两种［11］。结合前面模态分析结果，对链轮和链条进行谐响应分析采用模态叠加法，降低计算量。

4.2 载荷设置

根据铸铁机工况，链轮受到主轴传递的力矩，主要需要克服链条对链轮的拉力，此拉力主要是链条、铸铁模（含铁水）的重力，以及链条与支撑托辊之间的摩擦力。相关参数见表1。

表1 零部件参数

链轮受到的载荷主要为链条作用的拉力，直接施加设置。

4.3 谐响应分析

从模态分析的结果可以看出，链轮和链条的模态振型中容易发生变形的是链轮的外边缘和链齿，以及与链轮未完全啮合的链节。针对链轮容易发生弯曲和扭转变形，对其进行谐响应分析，得到幅频响应曲线，见图4所示。

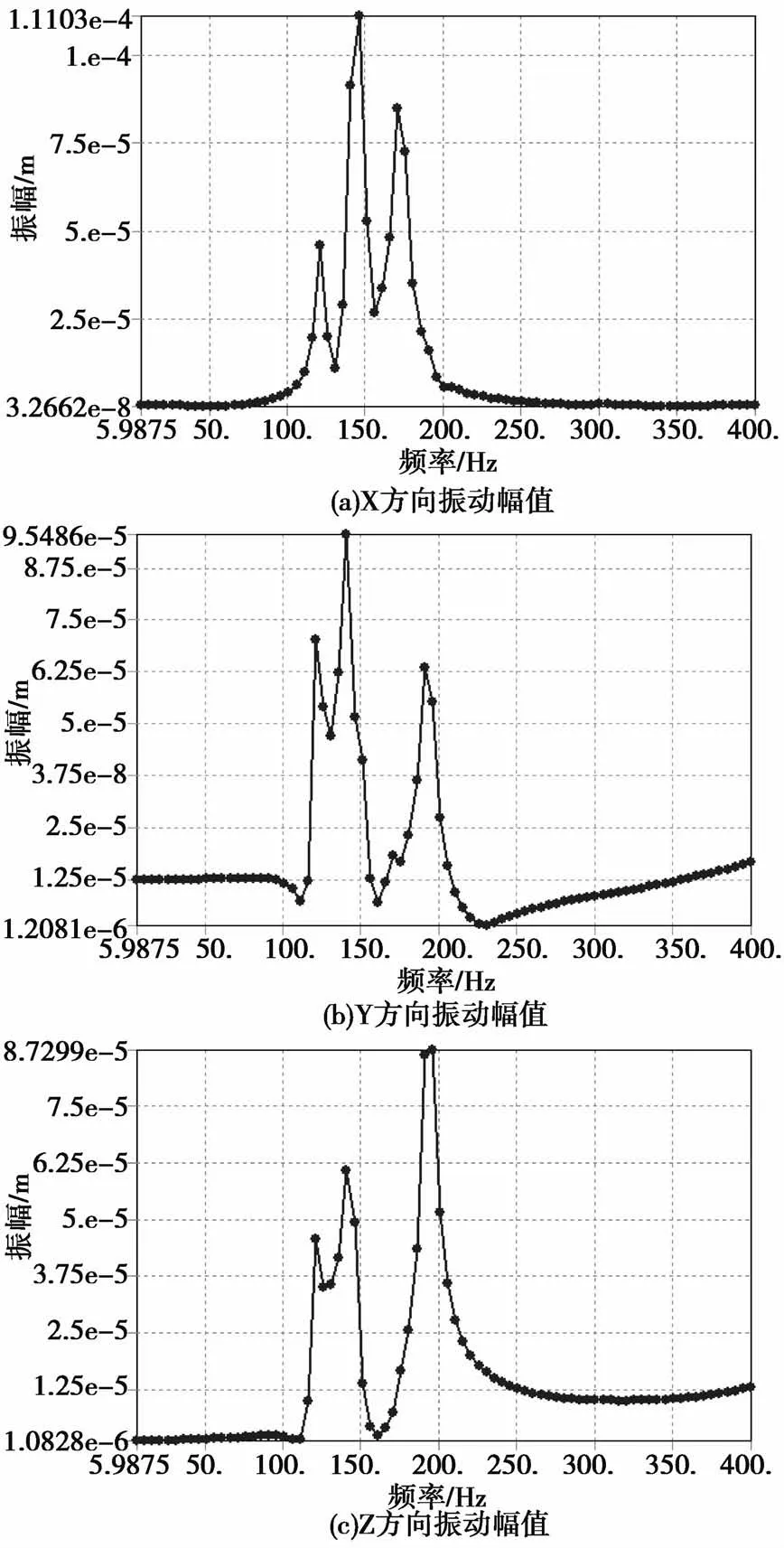
图4 链轮振动幅频图

从上图可以看，链轮在113Hz～200Hz之间，X方向出现幅值变化的过程，其中在143Hz时，振动幅值达到最大值，在其他频率时幅值也出现极值情况。在125Hz～220Hz之间，Y方向幅值出现波动，在这个过程中出现三次极值，其中在143Hz时，振动幅值达到最大值。在125Hz～235Hz之间，Z方向幅值出现变化，经历了三次极值过程，振动幅值达到最大值是在191Hz。X方向和Y方向上的振幅出现极值和最大值的频率是一致的。

针对链条容易发生弯曲变形，对其进行谐响应分析，得到幅频响应曲线，见图5所示。

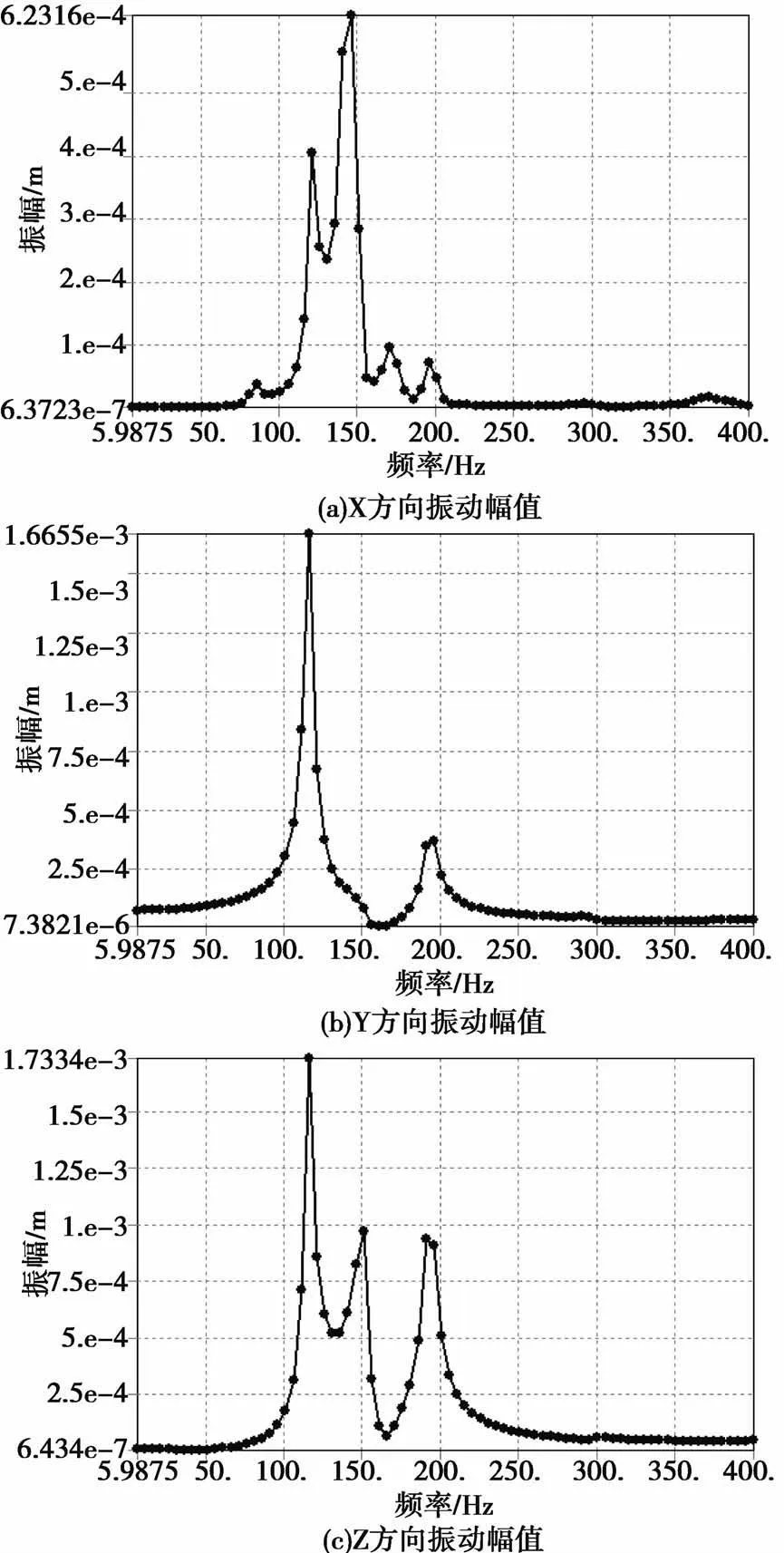
图5 链条振动幅频图

从上图可以看，X方向上，链条在频率115Hz～200Hz之间振动幅值出现变化，其中在143Hz时，幅值达到最大值，在其他频率值上出现三次极值情况。Y方向上，振动幅值在126Hz时达到最大值。Z方向上，幅值出现变化的频率区域是110Hz～213Hz之间，在126Hz达到最大值。Y方向和Z方向上的振幅最大值的频率是相同的，频率范围基本一致。

通过谐响应分析可以看出，链轮和链条产生极值振幅，主要是与其低阶固有频率部分重合，实际生产中，应该提高链轮和链条的固有频率，或降低外部激励频率，以避免出现链传动振动过大而引起的打滑和跑偏等问题。

5 结论

结合动力学理论，对铸铁机的链轮和链条进行了模态分析和谐响应分析，得到以下结论：

（1）链轮和链板的前5阶固有频率在170Hz～300Hz之间，振型主要是平面内的弯曲和扭转组合变形，以及绕链轮轴心线的弯曲变形。

（2）谐响应分析发现，幅值出现极值频率与链轮和链条的固有频率前3阶相重合。因此，需避免低阶频率的共振。实际生产中可以将链轮和驱动装置基础采用整体基础，与平台连接一体，降低振动过大，避免出现打滑或跑偏等情况。