基于组合模型的高铁隧道围岩收敛变形预测

李照众 王 浩 畅翔宇 张一鸣 王飞球

(1东南大学混凝土及预应力混凝土结构教育部重点实验室， 南京 211189)(2中铁二十四局集团江苏工程有限公司， 南京 210038)

隧道开挖会对周围岩体产生扰动，进而破坏围岩的初始应力状态，使围岩产生应力重分布以保持其稳定性.根据能量守恒定律，围岩应力随掌子面推进逐步释放，导致围岩产生收敛变形，直至围岩再次进入稳定状态[1].然而，围岩收敛变形过大可能导致局部落石，甚至引起隧道坍塌、突泥突水等重大安全事故.围岩收敛变形包含了当前围岩变形状态及未来发展趋势，对其进行及时监测和预测分析可在变形早期发现、解决安全隐患，保证人员安全及隧道的有序施工[2].因此，有必要建立准确的围岩收敛变形预测方法，及时评估隧道施工安全性，以防安全事故的发生.

围岩变形预测作为保证隧道施工安全的重要依据，是隧道领域研究的热点问题[3].随着计算机性能的不断提升，机器学习算法展现了高效的拟合、泛化能力，已成功应用于围岩变形预测中[4-8].人工神经网络作为一种具有大规模并行处理的监督式学习算法，广泛应用于隧道围岩变形预测中[3].姚凯等[4]针对软岩隧道围岩变形问题，建立了基于果蝇算法优化的神经网络预测模型，对隧道拱顶沉降和水平收敛进行了预测.岳岭等[5]综合考虑了隧道施工中时间序列和变形多因素多元输入影响，建立了基于时间序列的自回归神经网络预测模型，较好地预测了盾构施工引起地表沉降规律.Nsubuga等[2]采用多层感知器神经网络预测某高速公路隧道变形，结合现场实测数据进行了预测分析.然而，人工神经网络需要大量训练样本，且易陷入局部极小值，导致预测结果存在一定的误差.近年来，适用小样本学习的支持向量回归算法(support vector regression, SVR)逐步应用于围岩变形预测[6].Shi等[7]将拱顶沉降数据转化为三角模糊粒子，建立了基于信息粒度化的SVR算法围岩变形预测模型.周奇才等[6]提出了一种基于离散小波消噪和动态在线滑移窗的SVR预测模型，用于消除地铁隧道变形监测数据受环境等因素引起的噪声影响.以上研究主要是基于数据驱动的围岩变形预测研究，并未考虑其物理特性，导致预测结果欠佳[8].高速铁路隧道对于围岩收敛变形要求极其严格.因此，围岩收敛变形预测应考虑监测数据本身的物理特性，以提高预测精度.

本文以阳山高铁隧道为工程背景，选取浅埋段的围岩收敛变形数据，采用基于贝叶斯参数优化的经验预测模型，获取初步预测结果.然后，采用SVR算法对预测结果进行修正，构建高铁隧道围岩收敛组合预测模型，以提高收敛变形的预测精度.

1 高铁隧道围岩收敛组合预测模型

高铁隧道围岩收敛组合预测模型主要包括隧道收敛经验预测、误差学习和预测结果修正3个部分.

1.1 隧道收敛经验预测模型

围岩收敛变形是反映围岩安全状态的重要参数，对其进行预测分析有利于解决可能存在的安全隐患，保证隧道施工安全有序[9].一般来说，围岩收敛由下面2种效应引起: ① 掌子面推进产生的岩体应力重分布效应；② 岩体随时间变化产生的流变行为[10].隧道收敛经验模型根据大量实测数据建立，具有适用性强、计算简便等特点，可实现监测数据的快速预测分析，并已运用于大量工程中[11-12].在本研究中，采用Sulem等[13]提出的收敛经验模型(EM)，并对其进行贝叶斯参数估计，优化EM模型的预测性能.

掌子面推进引起的岩体应力重分布效应会导致围岩收敛变形，其计算公式为

(1)

式中，x为测点到掌子面的距离；X为掌子面所影响的特征长度；C∞x为不考虑随时间变化影响下掌子面推进速度接近无穷大时的收敛值.

当隧道开挖短暂停止或测点距离掌子面较远时，收敛主要由随时间变化的围岩力学性质决定.围岩收敛随时间变化产生的变形可表示为

(2)

式中，t为测点所在断面自开挖后的时间；T为与时间相关的特征参数；Ax为与掌子面的距离相关的参数，且Ax/Cx(x)=m.当隧道断面具有相似的特征 (如岩体性质、开挖方法、支护等) 时，其m值大小相近[14].

隧道收敛变形经验模型C(x,t)为

(3)

采用EM模型时，需设定X、C∞x、T、m四个参数.为获得较为准确的模型，本文采用贝叶斯参数估计算法优化经验模型参数.首先，假设4个参数相互独立，并从文献[13]中获取其先验分布；其次，根据实测数据建立参数似然函数；最后，将先验分布和似然函数相乘得到参数的后验分布，以预测收敛变形[15].

马尔科夫链蒙特卡洛方法(MCMC)是贝叶斯计算方法中常见的一种模拟方法[13].本文基于MCMC方法计算经验模型参数的后验分布，进而构建贝叶斯参数估计下围岩收敛经验预测模型.

1.2 基于支持向量回归的误差修正模型

SVR算法是一种以统计学习理论为基础，用于数据分析和模式识别的有监督学习方法，已广泛应用于函数拟合等机器学习问题中[16].隧道经验收敛模型主要考虑岩体应力重分布引起的变形，未考虑施工中不确定性因素(如光面爆破、地下水、不规范施工等)引起的围岩变形，导致EM模型预测结果中存在残差项E={e1,e2,…,ej}(j=1,2,…,n)[8].由于SVR算法在解决小样本、非线性及高维模式识别问题中表现出良好的泛化性能，因此本文采用SVR算法对EM模型的残差E进行滚动学习，进而修正其预测结果.

假设误差学习最佳历史序列数目为p，则误差修正模型的输入样本为L=[l1l2…li],i=1,2,…,n-p，其中，li={ei+1,ei+2,…,ei+p}为输入样本，y={y1,y2,…,yi}={ep+1,ep+2,…,ei+p+1}为输出样本，n-p为训练样本数.SVR算法目的在于寻找满足回归要求的超平面，使训练数据尽可能地接近超平面函数f(L)=ωL+b，最优超平面函数即为所求误差修正模型，其中ω为权重向量，b为偏置.

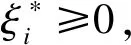
(4)

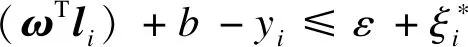
式中，ε为不敏感系数；c为惩罚参数.

求解目标函数式(4)可得

(5)

隧道围岩变形具有强非线性，因此本文采用RBF核函数，其对应的映射函数将样本空间映射至无限维空间[17].RBF核函数公式为

(6)

式中，σ核函数参数.

1.3 围岩收敛组合预测模型

采用EM-SVR算法预测隧道收敛变形，主要步骤如下：

① 采用贝叶斯参数估计算法优化EM模型参数，建立初步隧道收敛预测模型，预测收敛变形趋势项，并根据预测结果计算预测残差项E.

② 根据EM模型的残差建立学习样本，以降低均方误差(RMSE)为原则，选择合适的惩罚参数c、核函数参数σ以及最佳历史序列数目p，构建基于SVR算法的误差修正模型.

③ 通过RMSE与平均绝对百分误差(MAPE)验证误差修正模型合理性，RMSE、MAPE值越小，则该模型的性能越好，其计算公式分别为

(7)

(8)

④ 根据误差修正模型修正经验模型的预测结果，并将修正结果作为隧道最终收敛变形预测值.

2 工程应用

依托阳山高铁隧道工程，开展基于EM-SVR算法的围岩收敛预测研究.该隧道采用新奥法施工，里程DK57+285-DK57+445为Ⅴ级围岩区，其岩体极为破碎，围岩自稳能力差.Ⅴ级围岩区采用三台阶法施工，其开挖工法、支护措施等在整个隧道施工中最具代表性.为保证人员安全以及施工有序开展，自2019-12-10起，开展了为期30 d的隧道水平收敛监测，测点布置见图1.为提高预测结果的精度，以监测时间长、数据完整为原则，选取其中1个断面的2个水平收敛测点进行预测分析，测点监测数据及其掌子面推进数据见图2.由图可知，随着开挖后时间的增加以及工作面推进，测点收敛变形整体呈增大趋势，且数据发生剧烈波动.

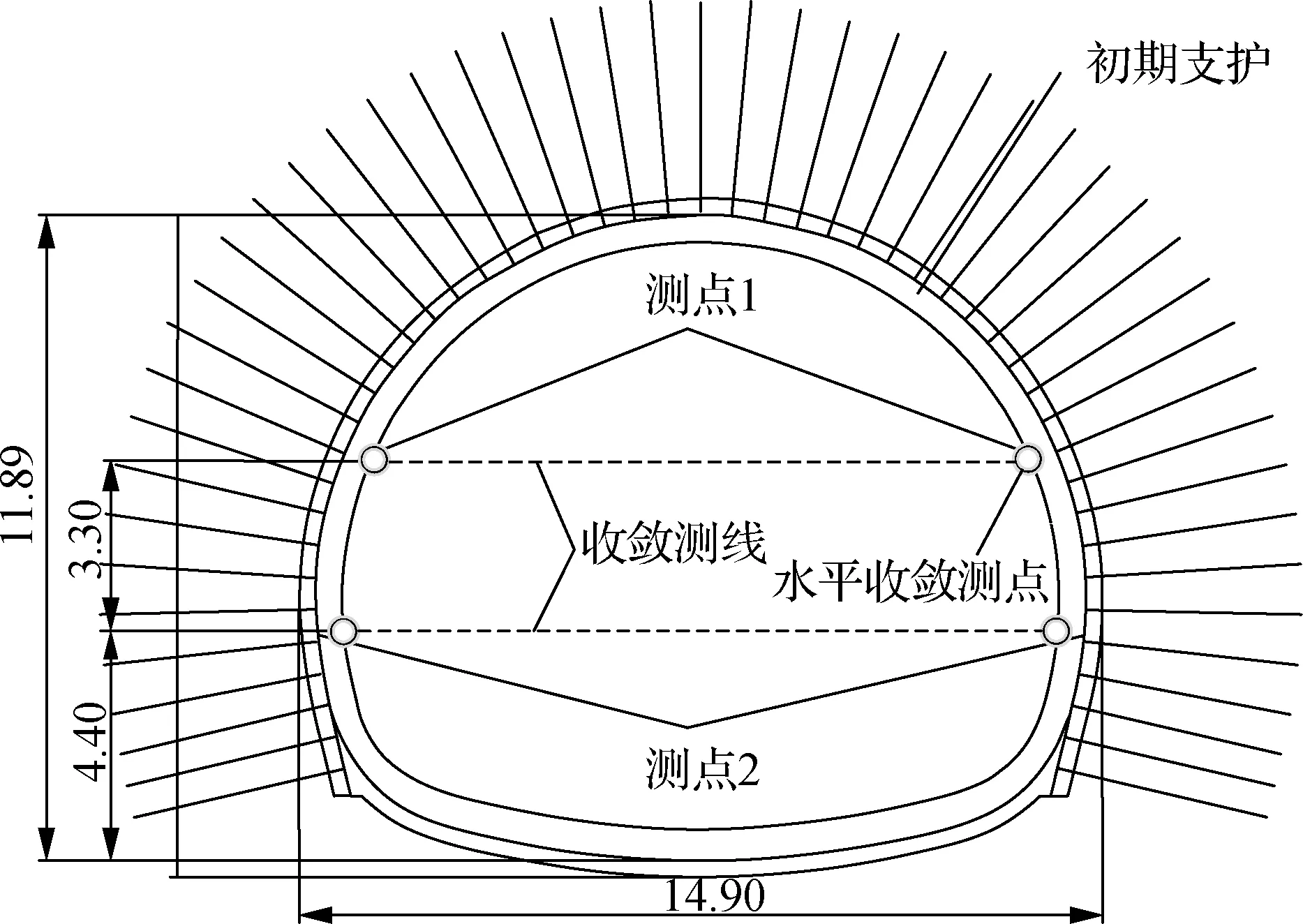
图1 隧道测点布置图(单位：m)

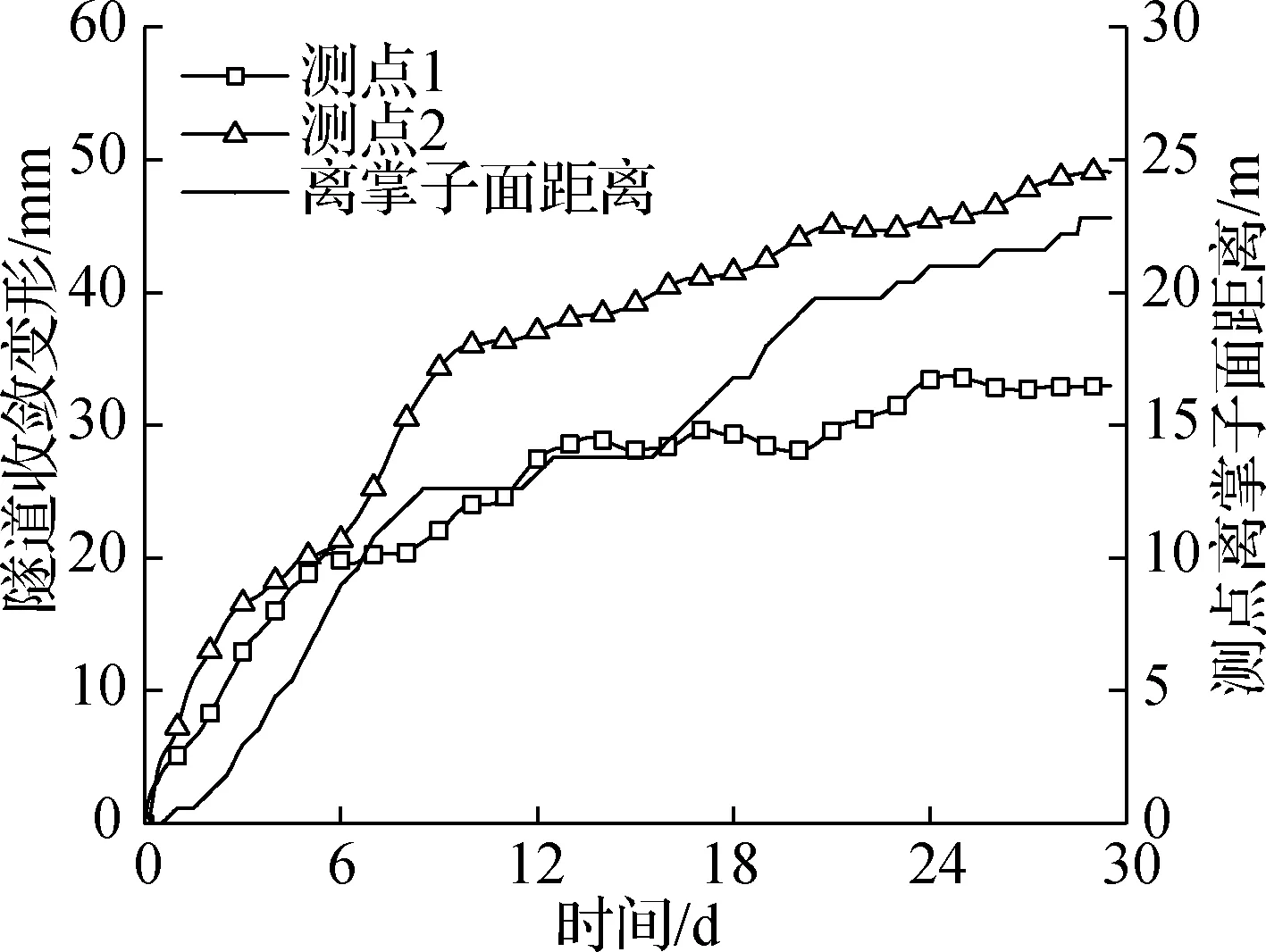
图2 测点监测数据以及掌子面推进数据图

因此，为保证隧道安全施工，应根据已有监测数据，构建围岩收敛预测模型.

2.1 EM模型的建立

采用基于贝叶斯参数优化的收敛经验模型，对阳山隧道的收敛数据进行预测分析.根据文献[13]确定EM模型参数的先验分布，结果见表1.虽然文献[13]中包含参数C∞x和m的统计结果，但波动性较大，故采用均值分布反映其先验信息.

表1 EM模型参数的先验信息

利用表1中参数先验信息和图2中的监测数据，采用MCMC方法对EM模型参数进行贝叶斯估计，共生成5×104个样本.对样本进行统计分析，得到EM模型参数在2个测点数据集中的后验分布(见表2).由表可知，除C∞x外，EM模型的参数估计在2个测点数据集中变化较小；这是因为2个测点处于同一断面，具有相似的地质结构和岩体性质，而C∞x参数在不同测点数据中存在较大差异，这与文献[13]中结论一致.

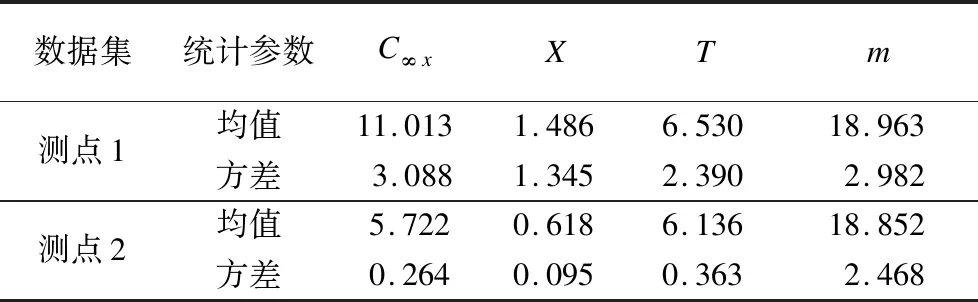
表2 EM模型参数后验分布

根据表2中的EM模型参数分布，构建收敛经验预测模型.该模型在2个数据集中所对应的RMSE值分别为1.834和1.258，预测结果及其95%置信区间见图3.由图可知，对于2个数据集，预测值与实测值变化趋势类似，说明该模型具有较好的预测性能.作为一个较为简单的函数模型，经验模型对数据中的波动部分无法做出准确预测.在测点1的数据集中，几乎所有实测收敛值都落在95% 置信区间内，但由于数据本身波动较大，导致置信区间范围也较大.在测点2的数据集中，数据整体波动较小，故置信区间范围比测点1小.

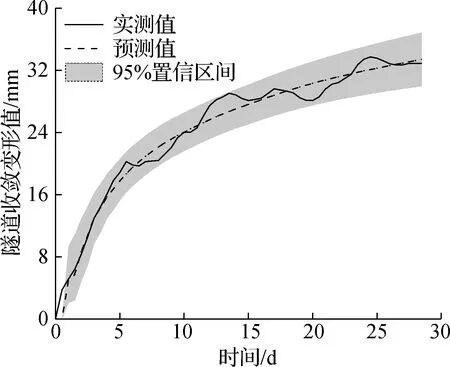
(a) 测点1

图4给出了EM在2个数据集中的预测残差曲线.由图可知，2个数据集的预测结果均存在明显残差，说明EM模型对平滑数据具有较好的预测能力，而对于数据中的波动成分预测能力欠佳.较大的预测残差将导致预测结果产生较大偏差，进而影响隧道安全评估的准确性.

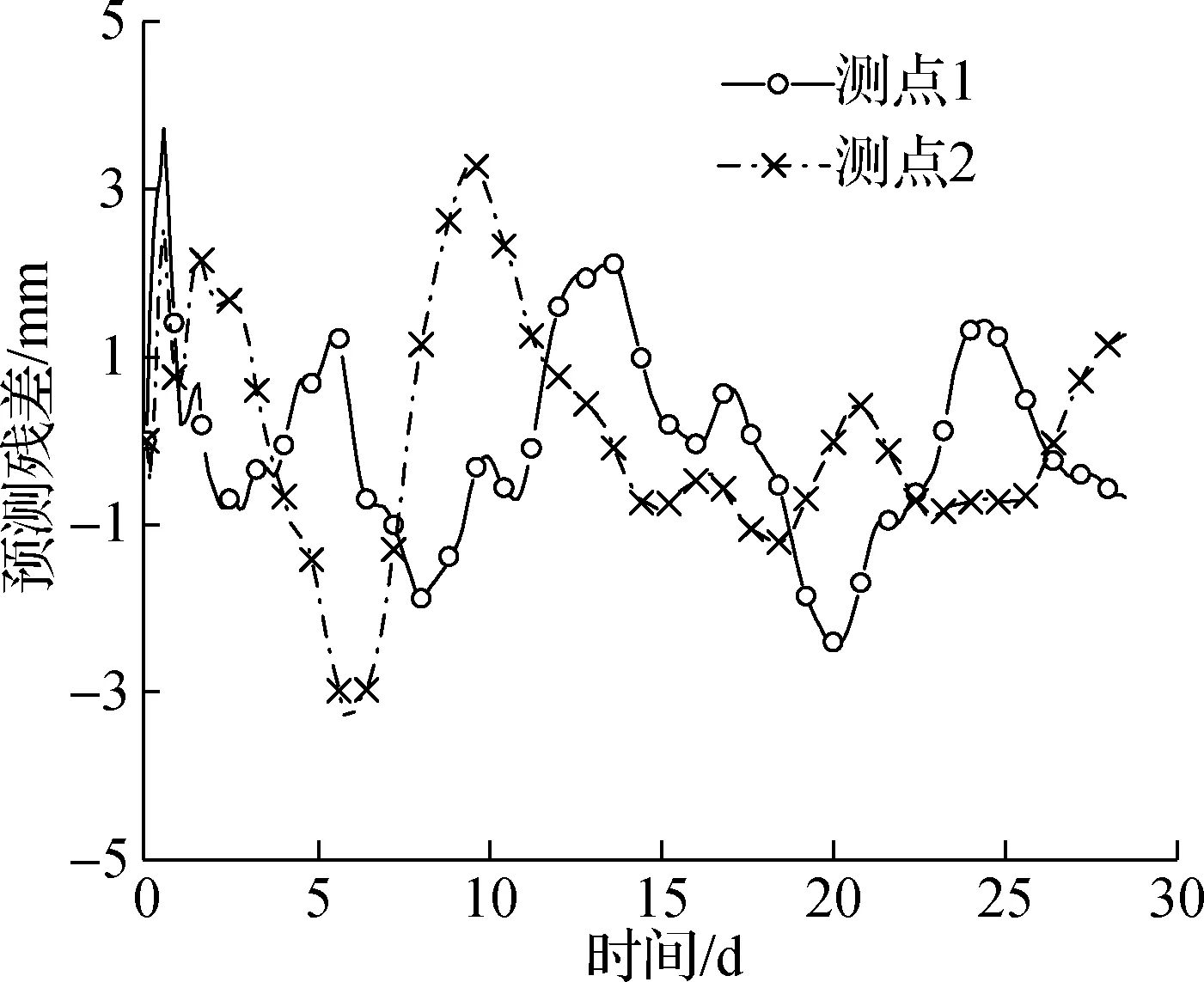
图4 经验模型的预测残差曲线

2.2 误差修正模型的建立

SVR算法是一种以结构化风险最小化原则构建的回归方法，不仅能使训练经验风险最小，而且极大地降低了模型复杂度[15].本文采用SVR算法修正经验模型的预测结果，提高隧道收敛变形的预测精度.

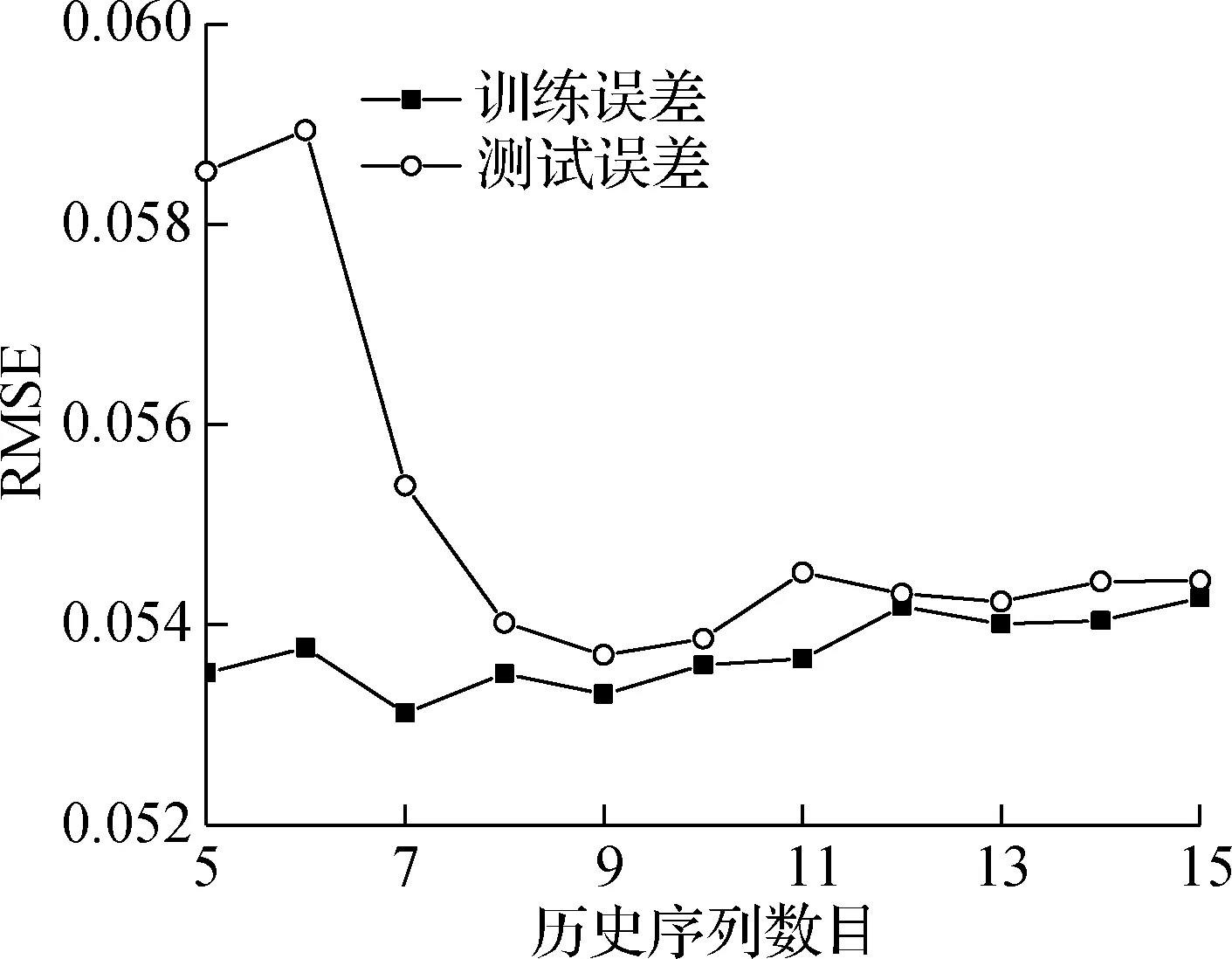
为确定预测精度最高的历史序列数目p，根据经验预测结果的残差项，选取不同的p建立基于SVR算法的误差修正模型，并计算训练样本和测试样本的RMSE值.首先，对训练数据进行初步试算，确定历史序列数目p的范围为[5, 15]，构造相应的训练样本和测试样本.然后，采用K折交叉验证法(K=10)[18]，训练基于SVR算法的误差修正模型.最后，将测试样本输入误差修正模型，训练样本和测试样本的RMSE值见图5.

(a) 测点1

由图5可知，对于训练样本，不同历史序列数目对于训练结果RMSE值的影响较小，整体呈现平稳趋势.对于测试样本，其RMSE值随着历史序列数目p的增加而变小，并逐渐趋于平稳，最优历史序列数目为9，2个测点训练样本集对应的RMSE值分别为0.053 7和0.083 5，RMSE相较于EM模型预测结果明显降低，说明基于SVR算法的误差修正模型展现出更好的学习性能.最优历史序列数目所对应的预测结果见图6.

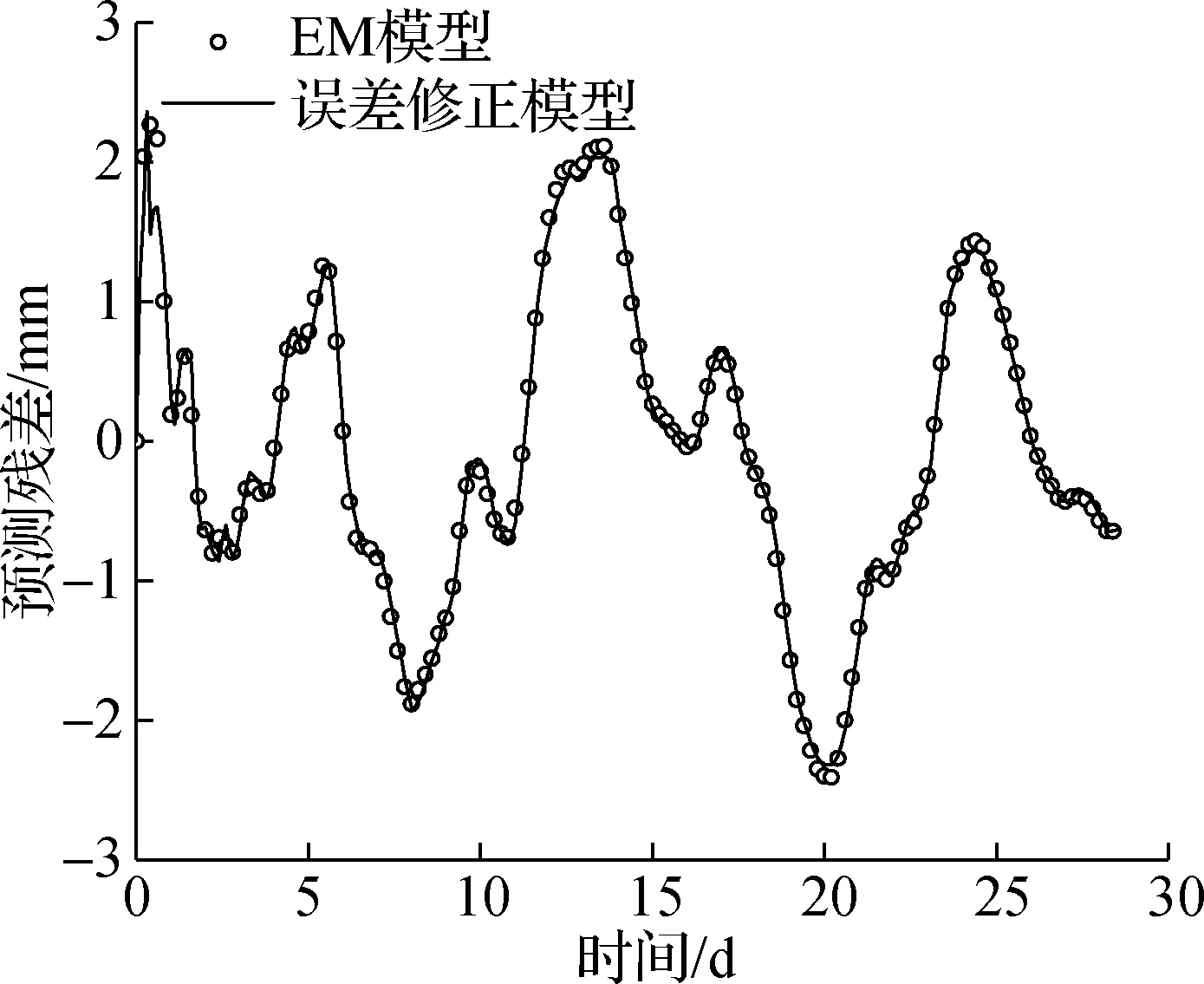
(a) 测点1

2.3 预测结果分析

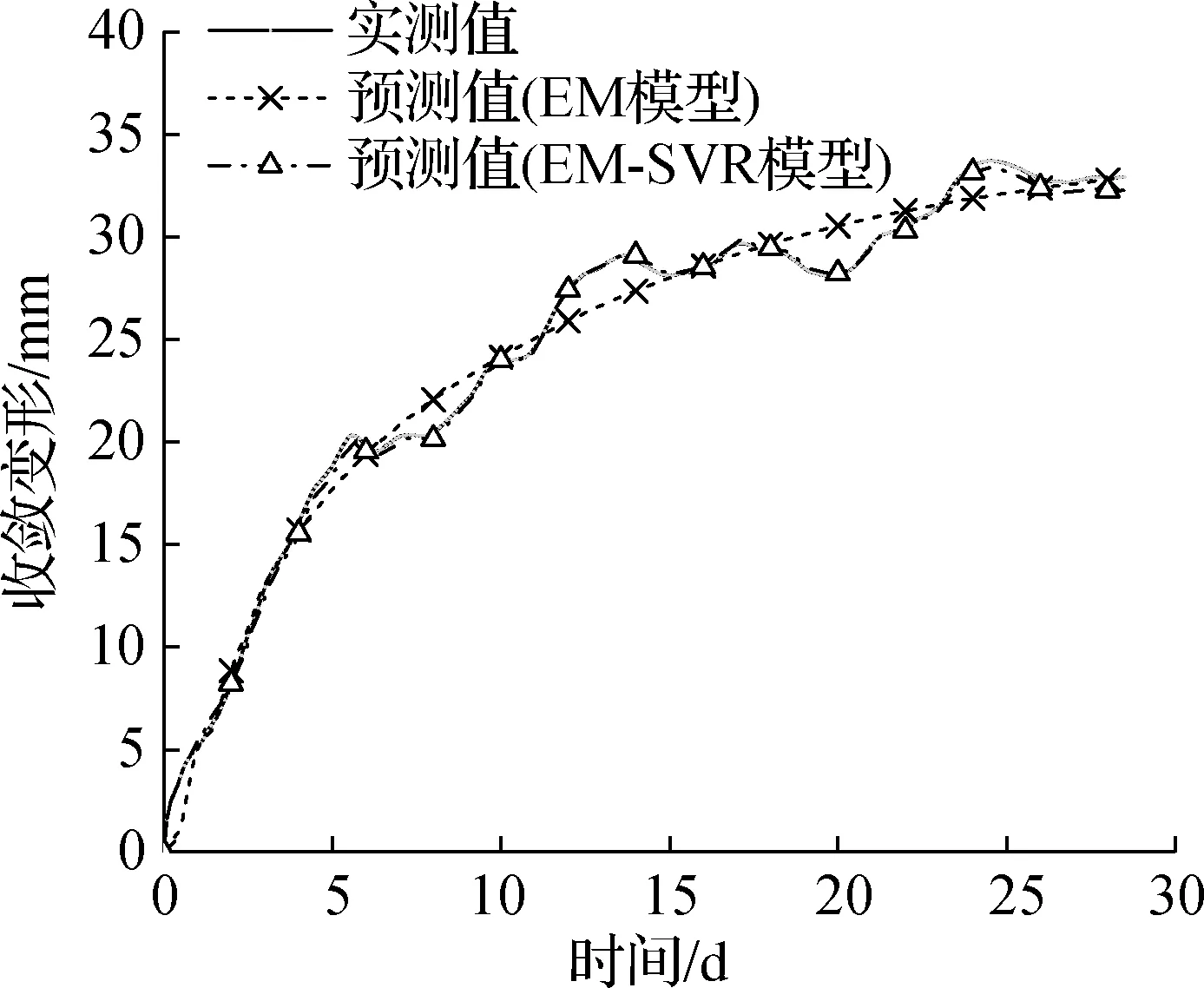
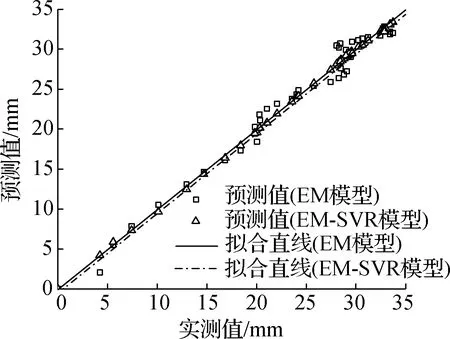
根据误差修正模型预测结果，修正EM模型预测结果，进而建立基于EM-SVR模型的收敛组合预测模型.图7给出了EM模型与EM-SVR模型的收敛变形结果.可以看出，2个模型的预测值与实测值表现出相似的变化趋势.误差修正后模型预测精度明显提高，尤其是针对监测数据中波动部分的预测.EM-SVR模型在2个数据集中的RMSE值相较于EM模型分别降低了97.0%和93.4%.为进一步对比2个模型的性能，将围岩水平收敛实测数据与预测数据进行对比，分析两者之间的差异，结果见图8.

由图8可知，EM模型和EM-SVR模型预测结果对应的数据点基本分布在y=x附近区域，且其相关性均高于95%.2种模型在测点2数据集上性能较为相近.EM模型在波动性较小的数据中具有良好的预测性能，而对于波动性较大的测点1数据集，采用EM-SVR模型可以大幅提高模型的预测性能.

2.4 模型对比

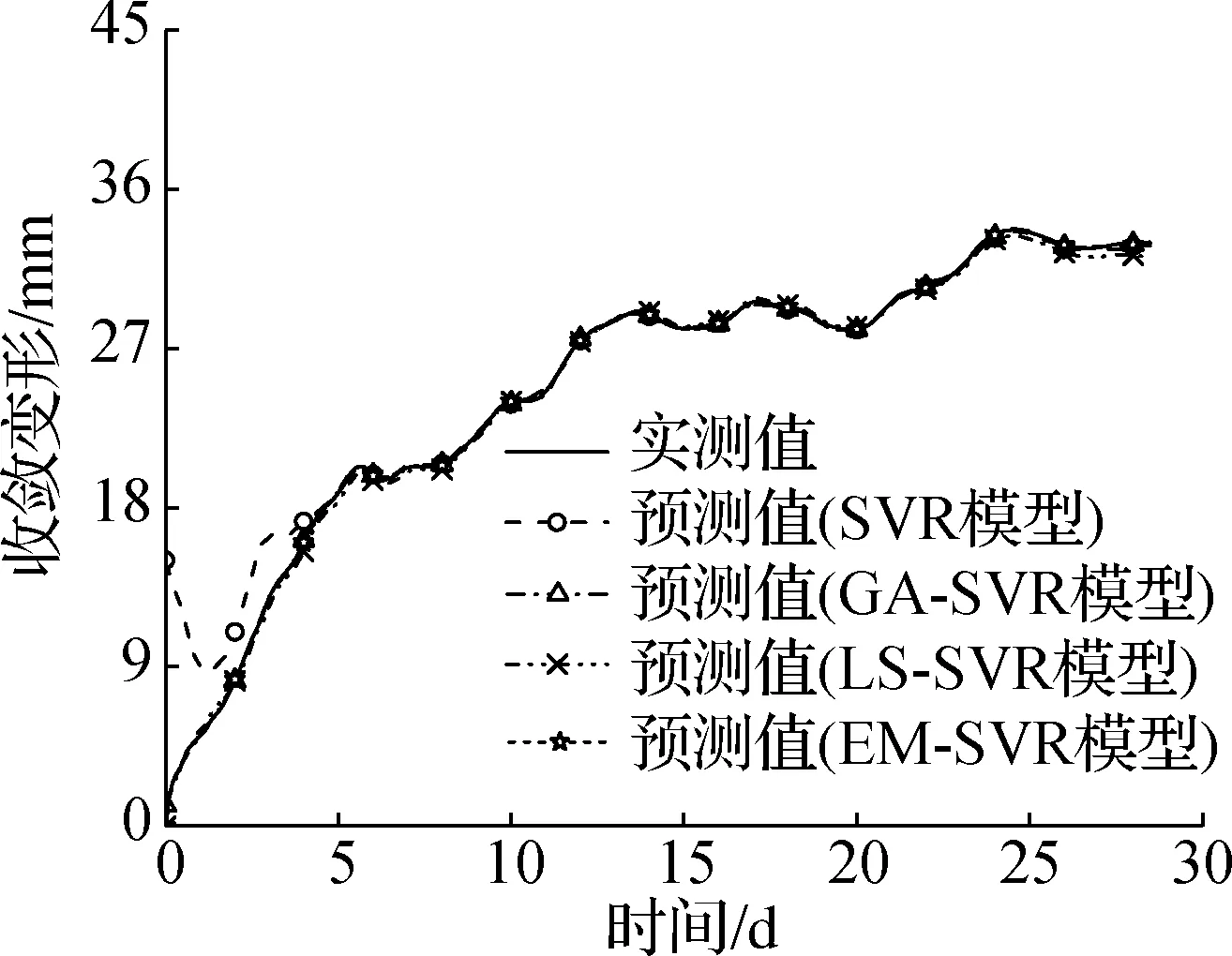
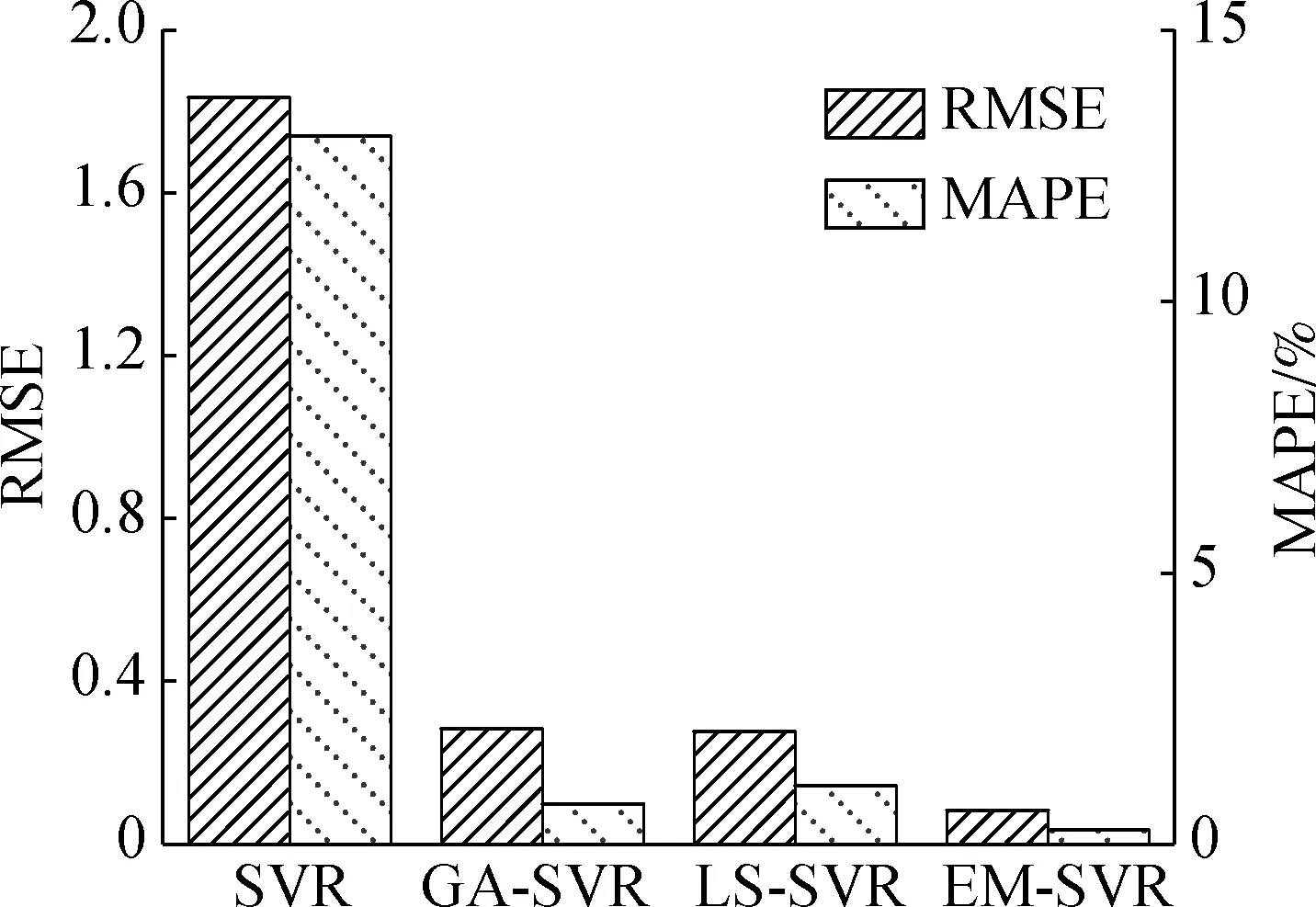
为比较不同模型的收敛变形预测性能，分别采用SVR模型、基于遗传算法(GA)优化SVR算法的预测模型、最小二乘支持向量回归模型(LS-SVR)进行预测对比.其中，GA算法在优化非线性函数方面表现优越，计算速度快，通常可找到全局最优解，避免陷入局部最优解.因此，采用GA算法对SVR模型的超参数进行优化，建立基于GA-SVR算法的收敛变形预测模型.LS-SVR模型利用二次损失函数取代SVR模型中不敏感的损失函数，并将SVR模型中的不等式约束条件改写成等式约束，具有计算效率高、收敛速度快等优点[19].SVR、GA-SVR和LS-SVR模型采用与EM-SVR模型相同的训练样本、测试样本及相关参数设置.SVR、GA-SVR、LS-SVR和EM-SVR模型预测结果见图9，其RMSE和MAPE值见图10.

(a) 测点1

(a) 测点1

(a) 测点1

由图9和图10可知，在2个测点数据集中，SVR模型的预测结果最差，尤其是在数据初期时，其对应的RMSE和MAPE值最高.利用GA算法对SVR模型进行参数优化，得到GA-SVR预测模型，性能得到显著提高，说明参数优化对SVR模型性能有显著影响.在测点1数据集中，LS-SVR模型与GA-SVR模型性能相近，而在测点2数据集中，GA-SVR模型的RMSE和MAPE值分别为0.110 4和9.391，均低于LS-SVR模型对应值，说明GA-SVR模型性能总体优于LS-SVR模型.EM-SVR模型的RMSE和MAPE值均低于其他预测模型，且EM-SVR模型较好地考虑了围岩收敛监测数据的物理特性.因此，基于EM-SVR算法的高铁隧道围岩收敛组合预测模型具有较好的适用性.

(a) 测点1

3 结论

1) 采用基于MCMC模拟的隧道收敛经验概率预测算法，考虑了掌子面推进引起的岩体应力重分布以及随时间变化产生的流变效应，隧道收敛预测值与目标值随时间变化的趋势一致，表明经验预测模型具有较好的适用性，且其参数后验信息可供相邻断面变形预测参考.对于数据中的波动部分，预测值与目标值存在较大偏差，说明该经验模型需进一步优化.

2) 采用基于SVR算法的误差修正模型对经验收敛模型的残差进行预测，进而修正经验收敛模型的预测结果.结果表明，选取合适的历史序列数目后，误差修正模型的性能明显提高.此外，对于监测数据中的波动部分，EM-SVR模型表现出较好的预测精度.

3) 基于相同的训练样本，SVR、GA-SVR、LS-SVR和EM-SVR四种模型的预测结果与实际数据随时间变化的趋势基本吻合.EM-SVR模型预测结果的RMSE和MAPE值都低于其他3种模型，表明EM-SVR模型具有更好的实用性，可为预测隧道水平收敛提供可行的方法.