基于转矩控制的上坡辅助电控系统
2021-10-21沙文瀚任彦君殷国栋章友京
沙文瀚 刘 琳 任彦君 彭 湃 殷国栋 舒 晖 章友京
(1东南大学机械工程学院, 南京 211189)(2奇瑞新能源汽车股份有限公司, 芜湖 241000)
坡道起步作为车辆的常见行驶工况,需要驾驶员协调控制油门和制动,若操作不当会造成溜车事故.为提高车辆行驶的安全性与操纵便捷性,研究人员开发了不同形式的上坡起步辅助系统.针对重型商用车,在制动主缸与制动工作缸之间加装坡道起步辅助阀能够实现坡道保持功能[1].当车辆检测到自身处于坡道起步状态时,在驾驶员松开制动的瞬间,坡道起步辅助阀作动,截断制动器工作缸与制动主缸之间的通路,保持一定时间的制动油压,使驾驶员有足够的时间操纵加速踏板[2].Peng等[3]针对这类具备电子制动控制系统的底盘结构,提出了一种对车辆质量进行自适应估计补偿的驻坡控制方法,解决了商用车质量变化导致的控制失准问题.此外,PID控制[4]、逻辑门限值控制[5]等方法也能有效解决基于电子驻车制动系统的商用车坡道辅助控制.塔塔汽车公司在其客车产品上开发了一套坡道辅助控制系统,通过调节AMT传动系统动力输出实现起步驻坡[6].针对AMT车辆大坡道起步过程中离合器摩擦片磨损严重的问题,刘海鸥等[7]提出了坡道起步改进控制策略,对车辆坡道起步过程进行划分并针对性建立了滑摩功优化策略.Song等[8]提出了一套适用于装备AMT车辆的离合器控制双层架构,有效解决了车辆起步时的溜坡和顿挫感较强的问题.此外,还有基于坡道传感器的控制系统成功应用于燃油汽车平台[9].
针对混合动力乘用车,Zhao等[10]提出了离合器与混合动力系统的协同控制方法,通过建立扰动有界的线性模型并设计了H∞鲁棒控制器,保证自动驻坡算法的鲁棒性.为了解决发动机自动启停时的起步控制问题,Tang等[11]提出了一种考虑双电机耦合辅助驱动的混合动力车辆起步控制方法,在保证车辆平稳起步的同时能够有效降低系统能耗.针对乘用车的驻坡控制,Wu等[12]通过分析车辆在行驶过程中的纵向力变化率,提出了一种基于扭矩动态分配策略的坡道起步辅助方法,并使用逻辑阈值理论实时控制轮缸压力,保证了车辆在坡道上的平稳起步.在纯电动汽车领域,Belousov等[13]设计了两通道冗余电动驱动器,通过合理地分配2套电驱系统的参与比例,提升了起步阶段车速控制的稳定性和准确性.此外,基于牵引力调节[14]和分布式动力协同控制[15]的方法也被用于解决坡道辅助控制问题.
总体来看,目前坡道辅助系统主要针对重型车辆应用研究,且由于这些车辆均以内燃机为动力源,因此往往需要综合考虑内燃机、传动系统和制动系统动态特性,算法设计相对保守,用户体验仍有待优化.电动汽车能够直接控制电机产生准确驱动力,为坡道辅助控制提供了理想的执行机构和全新实现方式,但现有研究却鲜有专门针对电动汽车的驻坡控制算法.因此,如何设计适合于纯电动汽车的上坡辅助控制方法,且该方法是否适用于实际量产汽车仍有待进一步验证.
针对上述问题,本文提出了一种具备“反馈+前馈”结构的预加载转矩上坡辅助控制策略,利用坡道传感器提供的坡度信息计算前馈预加载转矩,缩短系统响应时间,减小溜坡距离;利用轮速传感器建立反馈回路,基于比例-积分算法控制系统快速收敛,调节系统动态特性.在车辆坡道动力学模型基础上,建立了控制系统闭环传递函数,通过时域分析讨论了控制参数与系统稳定性、准确性和快速性之间的联系,从理论上证明了算法的有效性.开发了面向量产乘用车的坡道辅助控制系统,通过实车道路测试,验证了该算法的实际使用效果,并与目前广泛应用的纯PI调节和负载观测器调节技术进行了对比分析.
1 动力学模型
准确的数学模型是控制系统的设计基础,为此建立考虑坡道因素的车辆纵向动力学模型.驱动力是由电机的转矩经传动系统至驱动轮上得到的;行驶阻力包括滚动阻力、空气阻力、坡度阻力.
电机产生的转矩,经过传动系统传到驱动轮上,产生对地面的圆周力,此时地面对驱动轮的反作用力Ft为汽车的驱动力.可以得到轮端驱动力与驱动电机的力学传递关系如下:
(1)
式中,Tq为电机转矩;ig为减速器传动比;ηT为传动系统的机械效率;r为车轮半径.
ηT与减速器、传动轴万向节等传动系部件的功率损失有关,单级减速主减速器效率为96%,传动轴的万向节效率为98%.
车轮滚动时,轮胎与路面的接触区域产生法向、切向的相互作用力以及相应的轮胎和支撑路面的变形,则滚动阻力Ff如下:
Ff=mgfcosθ
(2)
式中,m为整车质量;f为滚动阻力系数;g为重力加速度;θ为坡度角.
汽车直线行驶时受到的空气作用力在行驶方向上的分力称为空气阻力Fω.空气阻力分为压力阻力与摩擦阻力2部分:压力阻力是作用在汽车表面的法向压力的合力在行驶方向的分力;摩擦阻力是由于空气黏性在车身表面产生的切向力的合力在行驶方向的分力.在汽车行驶过程中,空气阻力一般与气流相对速度μr的平方成正比,即
(3)
式中,CD为空气阻力系数,一般是雷诺数Re的函数,在车速较高、动压力较高而相应气体的黏性摩擦较小时,CD将不随Re而变化;A为迎风面积,即汽车行驶方向的投影面积;μr为相对速度,即无风时汽车的行驶速度;ρ为空气密度,一般ρ=1.225 8 kg/m3.
当汽车上坡行驶时汽车重力沿坡道的分力称为坡度阻力,如下式所示:
Fi=mgsinθ
(4)
由于本文关注的车辆驻坡工况,行驶车速很低,故忽略空气阻力,可得到汽车驻坡动力学方程为

(5)
其中,ig=7.88,r=0.3 m,ηT=96%×98%=94%,m取负载2人的整车质量1 000 kg,f取一般的沥青或混凝土路面滚动阻力系数0.02,坡道取15%的坡度.将以上参数代入式(5)中计算得到Tq=74.7 N·m,与实际驻坡稳定扭矩75 N·m接近,说明所建立的数学模型和选取参数与目标车型一致.
2 上坡辅助控制设计与分析
2.1 整体控制架构
图1为电动汽车上坡辅助控制系统架构图.整车控制器接收加速踏板、制动踏板、车速、坡道和档位等信息,判断车辆是否处于坡道起步工况并进行保护.这里档位信号主要是为了判断当前车辆状态是在前进档(D档)、倒车档(R档)还是驻车档(N档).电机控制器接收整车控制器发出的使能信号和预加载转矩进行坡道起步控制并输出控制转矩,通过正反转实现坡道起步过程.

图1 坡道辅助控制系统架构图
2.2 预加载转矩控制算法
在车辆即将发生溜坡时预先加载适当的驱动转矩是防止溜坡的有效方法.受制于坡度测量精度和汽车复合工况运行的限制,坡道阻力的精确计算十分困难,因此必须引入对车速的闭环控制对溜坡行为进行动态抑制.为了充分利用坡度传感器输出的参考坡道信息,提出了具备“前馈+反馈”结构的预加载转矩控制方法.
当车辆静置时坡度传感器能够测量出坡度大小,而坡度辅助算法恰恰就是通过施加驱动力矩平衡坡道阻力.考虑到小角度假设下sinθ≈θ,设计控制系统的前馈控制律为
Tpre=kθθ
(6)
式中,Tpre为前馈扭矩;kθ为前馈比例系数,表征了对预估坡道阻力的补偿比例.
将车速作为反馈变量,采用比例-积分(PI)控制作为反馈回路的控制算法,即
(7)
式中,Tfd为反馈扭矩;kp为比例控制系数;ki为积分控制系数;R为参考输入;Vx为纵向车速.
那么,总驱动扭矩Td为前馈回路与反馈回路的扭矩计算之和,即
Td=Tpre+Tfd
(8)
结合车辆纵向动力学模型,对上述公式进行拉普拉斯变换,整个控制系统的控制框图如图2所示,其中s为拉普拉斯算子.

图2 预加载转矩调节控制框图
由于本文研究的应用场景为驻坡控制,因此参考输入R(s)=0,可以得到系统坡道输入对车速变化的传递函数G(s)如下所示:
(9)
可以看出,所提出的预加载转矩调节控制系统是一个二阶系统.3个主要控制参数kθ、ki和kp会对系统的零极点分布产生影响,进而影响系统的稳态和动态性能.需要强调的是,如果令kθ=mgr,那么在任何坡道输入条件下车辆都能稳定在坡道上,不发生后溜.这种情况的物理含义是,前馈转矩产生的驱动力恰好和坡道阻力平衡.但实际工程中,受到传感器精度、整车质量变化以及环境扰动等多因素耦合影响,难以精确得到满足上述条件的前馈系数.同时,坡道辅助控制系统要保证车辆不能突然向前行驶,否则容易使驾驶人员产生紧张情绪和不信任感.因此,在乘用车的应用场景中需要使kθ略小于mgr,从而保证系统抗干扰裕度.
2.3 系统性能与控制参数分析
对于结构确定的控制系统来说,控制参数的选取至关重要,直接决定了系统响应的稳态性能和动态性能.因此,需要分析各控制参数对系统性能的作用机理,进而揭示控制参数的调节规律.
对于一个闭环控制系统,稳定性是系统最基础、最重要的性能.由上述构建的系统传递关系可以得到系统的极点s1,2如下:
(10)
因此,只要满足ki>0且kp>0,该控制系统就是稳定的,而kθ与系统稳定性无关.
下面分析系统的稳态误差.坡道辅助控制系统要求在经过一段调节时间后,车辆最终能完全停在坡道上,因此要求系统的稳态误差为零.由于在启用该功能前,车辆处于驻车状态,而启用该功能后坡道保持不变,因此不妨设系统输入形式为阶跃激励,即θ(s)=1/s,那么系统响应的s域表达如下:
(11)
在系统稳定的前提下,由终值定理可求得系统的稳态误差表达式如下:
(12)
式中,Vx,ss为稳态车速.
当ki≠0且kp>0时,所提出的坡道辅助控制系统没有稳态误差,也就是说最终能够将车完全停在坡道上.因此,在反馈的控制回路中积分环节是必不可少的一个重要结构,能够起到消除稳态误差的作用.
在得到了控制系统稳定和控制无静差条件后,需要分析各个控制参数对系统动态性能的影响.为了减少溜坡距离,需要保证系统有较快的响应速度,通常需要将二阶系统设计成欠阻尼系统.因此,控制系统的极点应当具有一对共轭复根,即
(13)
控制系统阶跃响应的时域解析表达式为
(14)
令Vx(tr)=0,可以得到系统的调节时间tr为
(15)
对于系统的峰值时间tp,可由图解法求得,即
(16)
由于该系统的稳态输出为零,因此无法通过定义得到系统的超调量.但为了分析车速的震荡变化行为,选择二阶系统的欠阻尼固有频率ωd和增益系数Kg进行替代分析,即
(17)
从上述解析结果可得,前馈系数对坡道阻力的补偿能力十分关键.如果能够通过标定获得相对准确的kθ,那么车速变化的范围能够被限制在一个令人满意的区间内,从而实现驻坡辅助的功能.通过调节kp和ki能够改善驻坡控制的动态性能,kp越大,调节时间会增加,但能够削弱系统震荡;ki越大,系统调节时间越短,但会加剧系统震荡.因此在标定中需要寻找到合适的控制参数组合,以综合满足乘用车的应用需求.
最后分析控制参数对溜坡距离的影响.对车速进行积分可得到如下车辆位移的时域阶跃响应的拉普拉斯变换:
(18)
式中,X表示车辆位移.
由终值定理可得车辆完全静止后的总位移为
(19)
式中,Xss表示位移的稳态值,也就是最终的溜坡距离.由于在标定过程中需要保证kθ 综上,将控制系统标定策略制订为:首先在不同载荷状态下通过静态试验确定坡道对应的前馈系数kθ,保证车辆不冲坡、不溜坡;然后再根据溜坡距离和实际响应的舒适度调整ki,若溜坡距离过长则需要适当增加ki,若溜坡距离能满足需求但系统震荡较强,则可以适当减小ki;如果溜坡距离和响应速度难以兼顾,则可以适当调整反馈回路比例系数kp后再调整ki,以获得满意的综合响应. 本文以某电动汽车为试验平台进行搭载测试,在15%的坡道上进行坡道起步测试,用于对比不同控制方法下的坡道起步效果. 本文以奇瑞新能源EQ1车型为试验车进行整车搭载测试,试验车主要参数为:峰值转速7 300 r/min,峰值扭矩120 N·m,峰值功率30 kW,减速比7.88,车辆整备质量985 kg,轮胎尺寸165/65 R15,最大爬坡度20%.上坡辅助控制系统的零部件有整车控制器、电机控制器、电机、坡度传感器、加速踏板及刹车等.其中,坡度传感器用于检测车辆在静态下所处位置坡度值;整车控制器用于监控加速踏板、制动踏板、坡度传感器、档位旋钮等实时状态,控制车辆安全运行;电机控制器用于执行整车控制器的命令,控制电机输出驱动力或制动力,对车辆进行驱动或制动. 作为控制算法的核心执行部件,驱动电机采用扭矩控制模式,采用了空间矢量脉宽调制技术,具有控制精度高、响应快的特点.图3为台架测试的电机扭矩响应时间. 图3 电机扭矩响应时间 CAN总线是一种串行数据通信总线,其通信速率最高可达1 Mb/s,此时最大传输距离为40 m.试验车CAN总线通信速率为500 kb/s,最长传输距离为3 m左右.整车CAN总线采用屏蔽的双绞线,具有较强的错误检测能力,通过监视、循环冗余校验、未填充和报文格式检查,使得未检测出的出错概率极低. CAN总线访问采用基于优先权的多主方式.CAN总线任一节点所发送的数据信息不包括发送节点或接收节点的物理地址.信息的内容通过一个标识符(ID)作标记,在整个CAN网络中,标识符是唯一的.网络中其他节点收到消息后,对该标识符进行检测,来判断该信息是否与自己有关,若有关,则进行处理;否则,将忽略. 标识符决定了信息的优先权.ID值越小,其优先权越高.CAN总线确保发送具有最高优先权信息的节点获得总线使用权,而其他的节点自动停止发送.总线空闲后,这些节点将自动重新发送信息. 整车控制器和电机控制器节点标识符优先级较高,仅次于车身控制器、制动防抱死系统、电子驻车系统以及气囊控制器,确保其信息能够及时发出.经测试,本文实验平台的通信总线负载率为26%~28%,相关节点的通信时延小于1 ms,因此能够满足实时性要求. 整车控制器和电机控制器以10 ms为周期进行通讯,以保证电机控制器实时更新整车控制器的指令,整车控制器实时监测驱动系统的工作状态.同时,整车控制器和电机控制器分别对对方的通讯进行故障检测,当对方失去通讯超100 ms以上时报通讯类故障,保护整车安全运行. 由于在试验过程中,坡道起步工况下车辆会晃动,轮胎也会在原地前后摇摆,导致刻度尺、卷尺等测量工具不方便测量,本次试验采用的是梯形估算法,估算车辆在坡道起步过程中的溜车距离.轮胎截面高度H1计算方法如下: (20) 式中,L1为轮胎宽度;S1为扁平率.因此,轮胎滚动半径r的计算方法为 r=H1+12.7L2 (21) 式中,L2为轮圈直径. 由于电机控制系统在整车上的通讯周期T为10 ms,因此每10 ms采集一组电机转速,如图4所示,使用梯形法则计算转速曲线下的面积Sn. 图4 基于梯形法则计算溜车距离 电机转一圈整车的溜车距离L3为 L3=2πr (22) 因车辆减速比i=7.88,整车在坡起过程的溜车距离L为 (23) 本文提出了预加载转矩调节的上坡辅助控制方法,并基于量产乘用车平台进行了实车试验,并与目前市场上已有应用的纯PI调节和负载观测器调节两大技术进行了对比.通过转速转矩变化、系统响应速度和整车舒适性等方面对比3种控制方法在坡道起步工况下的优缺点. 负载观测器根据整车的转动惯量和速度变化观测整车的负载,输出观测转矩,稳定时相当于PI调节的固定前馈.若以Tob表示负载观测器观测出的负载转矩,TPI表示PI控制调节输出的转矩,则电机实际输出转矩Tq为 Tq=Tob+TPI (24) 其中负载转矩Tob的观测器方程为 (25) (26) 式中,J为转动惯量;ω为电机转速;Bm为摩擦系数;Te为电磁转矩;α为电机位置. 电机作为有阻尼的弹性系统,当作用力过大时,会加剧系统的弹性形变,即PI参数过大时,虽然会提高系统的响应速度,但同时会引起系统剧烈振荡.图5为3组不同PI参数在15%坡道上的调试结果,测试电控系统驻坡控制的基础能力,并分析PI参数的影响规律.由图可知,当kp=1.5,ki=1.0时,电机转速和输出转矩振荡剧烈,转矩最大振荡幅值为120 N·m,上述现象说明该组参数kp过大;当kp=1.2,ki=1.0时,转矩振荡幅值和频率明显减小,转矩最大振荡幅值为70 N·m,说明减小参数kp有效;当kp=0.8,ki=1.0时,电机转速和转矩基本不振荡,转矩加载平滑,减少了中间振荡过程,表明该组PI参数为最佳参数.依据3.3节中的梯形法计算得到Sn为-34 340,溜车距离L约为14 cm. (a) kp=1.5,ki=1.0 综上,比较3组转速转矩曲线发现,减小参数kp能够使电机转速变化趋于平稳,削弱了系统振荡,减少转矩振荡时间;但是由于PI调节输出转矩变化较慢,使得系统稳定时间较长,溜车距离变长. 由于PI调节的局限性,不能满足坡道辅助功能要求的实时性和鲁棒性,因此在PI调节的基础上添加观测器调节.在15%坡道上,标定PI参数为kp=0.8,ki=1.0,测试负载观测器激活前后的转速转矩的变化,试验结果如图6所示. 依据3.2节中的梯形法进行计算,激活负载观测器后的溜车距离L约为8 cm;未激活负载观测器时的溜车距离L约为14 cm.对比负载观测器激活前后,可以发现PI调节的最大调节转矩接近100 N·m,负载观测器调节的最大转矩为120 N·m;在响应快速性方面,PI调节输出最大转矩需要500 ms左右,负载观测器调节输出最大转矩需要360 ms左右;在驻坡总调节时间方面,PI调节使整车在坡上停住需要1 300 ms左右,负载观测器调节使整车在坡上停住需要800 ms左右. 因此,负载观测器调节较纯PI调节可以缩短6 cm的溜车距离.但是负载观测器的转速输入是目标转速与电机反馈转速的差值,需要在溜车发生后作用,具有一定的滞后性;由图6可知负载观测器观测的负载转矩需要一定的时间收敛,导致溜车距离不能进一步缩短. (a) 激活负载观测器 预加载转矩调节包含预加载转矩加载方式和预加载转矩维持时间,本节分别对2个方面进行实车测试,以选择最优参数. 4.4.1 预加载转矩加载方式 在15%坡道上,标定PI参数为kp=0.8,ki=1.0,测试阶跃加载转矩和加载斜率2种方法时的转速转矩变化.阶跃加载转矩是指在整车控制器检测到溜车工况时,瞬间加载目标转矩.图7为阶跃加载转矩为90 N·m时的转速转矩变化图.增大阶跃加载转矩虽然可以减少转矩加载时间,缩短溜车距离,但由于车辆的悬置和悬架是弹性系统,转矩的阶跃变化会引起高频分量的激增,导致转速变化大,电机转速反复振荡,整车感受剧烈,舒适性差. 图7 阶跃加载时转速转矩变化 加载转矩斜率是指将预加载转矩分为2部分进行加载:一部分在制动释放前加载,另一部分在检测到溜车时按照一定的斜率加载.在制动释放前预加载转矩,由于此时制动抱死车轮,能够避免产生电机转速振荡问题.但是若驾驶员长时间不释放制动,可能会造成电机过热,而影响电机寿命,浪费能源,所以该转矩不能过大.综上,将预加载转矩分为以下2部分:① 驾驶员松开制动前加载20%驻坡转矩,减少转矩突变引起的车身抖动,增加车辆起步平顺性;② 当检测到溜车时,按照一定的斜率继续加载转矩.此时,若转矩加载过快,会引起系统高频分量的激增,加大阻尼弹性系统的抖动;若转矩加载过慢,虽然会增加车辆起步的平顺性,但是由于转矩的提升无法满足上坡辅助控制需求,会使车辆持续后溜,导致坡起功能失效. 图8为3组不同斜率加载转矩时转速转矩变化趋势,从15 N·m分别以0.5、0.75、1.0 N·m/ms的斜率加载到75 N·m.当转矩加载斜率为0.5 N·m/ms时,转矩加载时间为120 ms,电机转速振荡幅值约为90 r/min;当转矩加载斜率为0.75 N·m/ms时,转矩加载时间为80 ms,电机转速振荡幅值约为140 r/min;当转矩加载斜率为1.0 N·m/ms时,转矩加载时间为60 ms,电机转速振荡幅值约为185 r/min. (a) 斜率0.5 N·m/ms 因此,转矩加载斜率越大,电机转速振荡幅度越大,车辆起步冲击越大;转矩加载斜率越小,转矩加载时间越长,整车溜车距离越大,酿成事故的风险越大.综合考量,转矩加载斜率选择为0.75 N·m/ms. 4.4.2 预加载转矩维持时间 引入预加载转矩会导致转速振荡,需要把握预加载完成后PI介入调节的时间.PI调节输出转矩与电机转速偏差紧密相关,在进行PI控制时,若电机转速振荡较大,则PI输出的瞬时转矩很大,会加剧弹性系统的振荡.基于这方面的考虑,在预加载转矩完成后,增加一定的维持时间,过渡电机转速振荡环节,使PI调节介入时电机转速振荡幅度较小. 图9为在15%坡道和6%坡道上分别维持2倍转矩加载时间和1倍转矩加载时间时转速转矩变化趋势,转矩加载时间是在坡道上从20%驻坡转矩以0.75 N·m/ms的斜率加载到100%驻坡转矩的时间.在15%坡道上,1倍转矩加载时间和2倍转矩加载时间效果一致,PI调节介入时,转速偏差较小,不会引起输出转矩的突变.在6%坡道上,1倍转矩加载时间偏小,PI调节介入时转速偏差为正,导致输出转矩变小;2倍转矩加载时间较好,PI调节介入时转速较小,PI调节不会导致输出转矩突变. (a) 15%坡道2倍转矩加载时间 因此,预加载转矩维持时间定为2倍转矩加载时间.图10为预加载转矩调节和纯PI调节的电机转速曲线对比,纯PI调节Sn为-34 340,溜车距离L约为14 cm;预加载转矩调节Sn为-7 615,溜车距离L约为3 cm,该方法可以缩短溜车距离约11 cm. 图10 电机转速对比 1) 针对纯电动汽车坡道起步时由于制动踏板和加速踏板操纵不及时引发的溜车问题,充分利用电机转矩响应快、驱动/制动转矩灵活可调的优势,设计了完全基于CAN总线反馈和控制所需信号的上坡辅助控制策略. 2) 设计具备“前馈+反馈”控制结构的预加载转矩调节方法,从理论上证明了该驻坡控制系统为无静差系统,能够实现车辆的驻坡控制.通过时域分析的方法,得到了各个控制参数与系统稳定性、动态性能之间的关系.只要使得反馈回路中PI参数均大于零,即可保证控制系统稳定,而与前馈系数无关;通过标定准确的前馈系数,能够减小系统的调节时间并缩短溜坡距离;比例系数决定了系统响应的平顺性,积分系数则决定了系统响应的快速性,因此在实际标定中需要综合考虑. 3) 搭建基于量产电动汽车的控制系统试验平台,通过实车道路试验的方式研究了纯PI调节、负载观测器调节和预加载转矩调节3种防溜坡控制算法对系统响应速度、溜坡距离以及整车驻坡平顺性的影响,分析了不同控制参数选取对驻坡控制响应的影响,并且标定了最优的PI控制参数.试验结果表明,预加载转矩调节控制方法最有效,缩短溜车距离约11 cm,坡道起步控制效果最优.3 试验平台搭建
3.1 试验平台
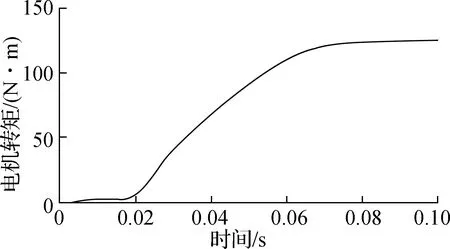
3.2 CAN总线通信设计
3.3 溜坡距离测量方法

4 不同控制方法实车试验对比与分析
4.1 对比算法设计
4.2 纯PI调节试验结果

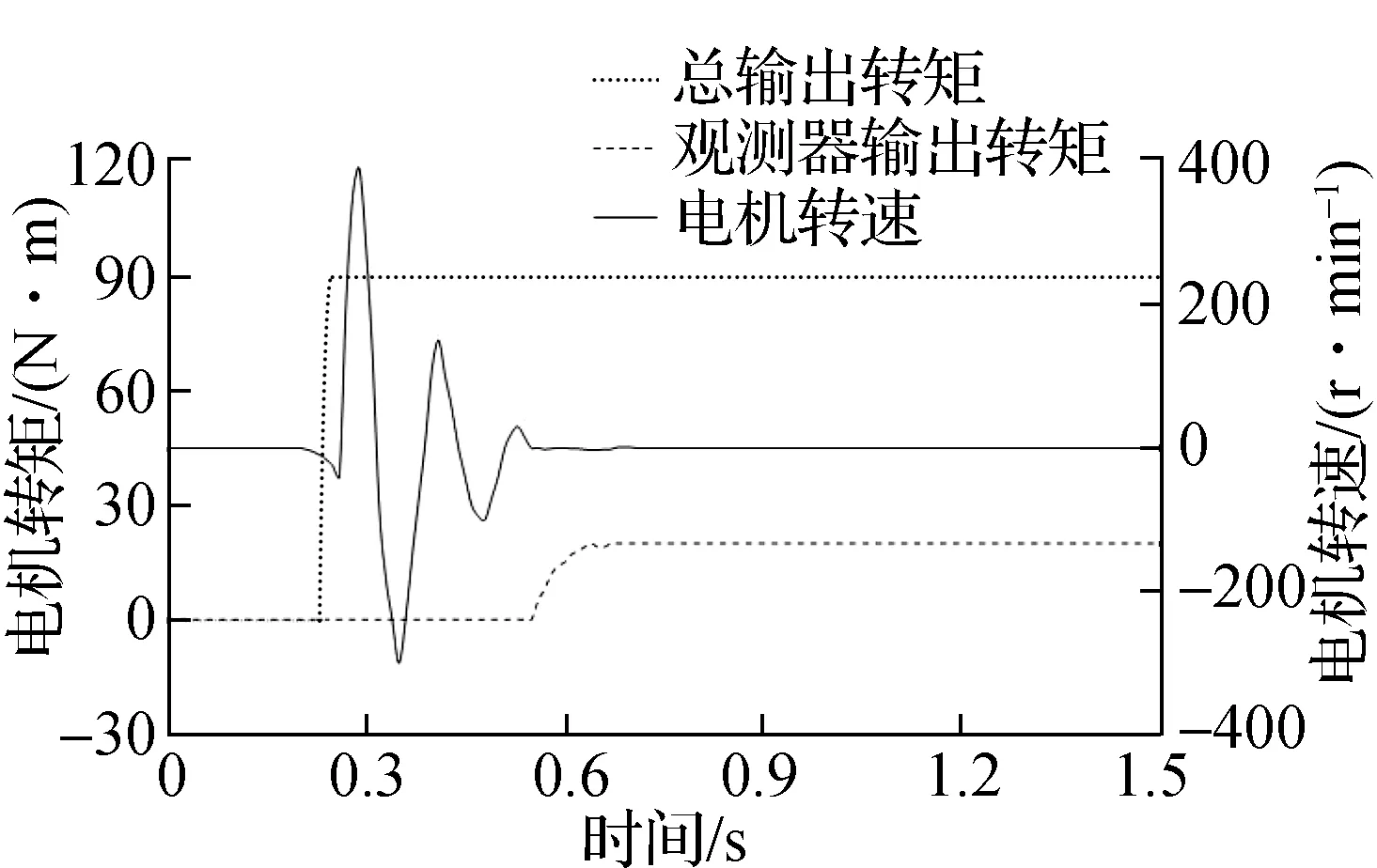
4.3 负载观测器调节试验结果

4.4 预加载转矩调节试验



5 结论
