基于Miura构形的折纸管抗屈曲能力研究

2021-10-21柳杨青蔡建国

东南大学学报（自然科学版） 2021年5期

柳杨青李旭蔡建国冯健

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)(2重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室, 重庆 400074)(3重庆交通大学土木工程学院, 重庆 400074)(4东南大学土木工程学院, 南京 211189)

折纸是一门古老的艺术,其将平面材料沿预设折痕折叠形成空间结构.由于折痕形式的多样性,通过折纸形成的空间结构多种多样.经过特别设计的折纸结构可以获得不同于常规材料的性能,从而在各领域得到了工程应用,如柔性机器人[1-2]、自折叠结构[3-4]等.由于力学性能表现良好、制造工艺简单且价格适宜,薄壁管状构件被广泛地用作吸能构件.圆管和方管是最常用的吸能薄壁管,其在轴向压溃作用下的力学行为得到了广泛的研究.研究人员通过数值模拟和试验研究,揭示了圆管和方管的变形模式和吸能特征,并提出了相应的分析理论和计算方法[5-7].研究还发现，圆管和方管在轴向压力作用下的变形模式对其初始几何缺陷十分敏感,使其吸能能力不易控制,而根据折纸构形的特点将其作为人为的初始几何缺陷施加于构件上可以激发特定的变形模式,由此控制荷载作用下的结构响应.这启发了研究人员将折纸构形引入到薄壁管上,形成了折纸型吸能构件的概念.

Guest等[8-10]将一种三角形化螺旋状圆柱折纸构形施加于圆管上,试验研究表明该构件在轴向荷载作用下可以实现完全折叠.Song等[11]首次提出了一种由等腰梯形构成的折纸管,数值模拟和试验研究表明该折纸构形成功诱导了构件在压溃荷载作用下的变形模式,从而改善了构件的耐撞性(crashworthiness).此后,研究人员设计了包括Miura构形[12-13]、crash box构形[14-15]、kite-shape构形[16-17]、waterbomb构形[18-19]等多种折纸构形,并将其应用于薄壁管上,这些构形均对荷载作用下的结构响应起到了良好的控制作用,并有效提高了构件的吸能能力.但当前研究的对象局限于长细比较小的折纸管,且研究集中于构件在冲击荷载作用下的力学性能,构件不会发生整体屈曲,而对于稍长的折纸管,构件存在发生整体屈曲从而失稳的趋势,并伴随构件跨中应力集中、突然的应力重分布和材料断裂等问题[20].因此,探索抑制稍长折纸管整体屈曲的方法具有重要意义.

本文将变角度Miura折纸构形引入到薄壁管上,并构建了一种折痕方案，以抑制该构件在轴心压力作用下的整体弯曲屈曲.首先介绍了一种由变角度Miura折纸构形合围而成的管状单元.将该单元堆叠形成基于变角度Miura构形的折纸管,并通过有限元分析比较了分别采用4种折痕方案的折纸管在轴心压力作用下的力学性能.将斜向谷线折痕设置为完美铰折痕,同时将其余折痕设置为连续折痕,能明显增强折纸管的抗屈曲能力,从而有助于提高其吸能能力.

1 基于变角度Miura构形的管状折纸单元

变角度Miura折纸构形,即二次折叠Miura折纸构形,是经典Miura折纸构形的衍生形式.两者之间的区别在于,经典Miura折纸构形中角度φ1=φ2,而变角度Miura折纸构形中角度φ1≠φ2,如图1所示,其中实线表示峰线折痕,虚线表示谷线折痕,l1和l2为构形的2条边长,2H为构形高度.当满足如下闭合条件[21-22]时,4个变角度Miura折纸构形可以合围组合而成基于变角度Miura构形的管状折纸单元:

(1)

式中,α为折叠角.形成的管状折纸单元见图2.

(a) 经典构形

图2 基于变角度Miura构形的管状折纸单元

2 基于变角度Miura构形的折纸管

2.1 折痕方案

刚性折纸是折纸构形的一个重要概念,即假定折纸面板的刚度无穷大,折纸构形可以随着面板绕完美铰折痕的转动而折叠和展开[23].完美铰折痕无法传递弯距,但可以传递剪力和轴力,本文将其称为A类折痕.然而在某些情况下,折纸构件可以通过模具冲压[15]、气压折叠[24]、3D打印[25]等冷成型技术进行制造.由此制成的折纸构件的折痕处材料是面板的延伸,材料截面并未削弱.此时,除剪力和轴力外,折痕还可以传递弯距,这类折痕为连续折痕,本文将其称为B类折痕.通过将不同位置的单元折痕设置为A类折痕或B类折痕,可以得到如表1所示的4种折痕方案,其中的水平折痕、斜向峰线折痕和斜向谷线折痕如图2所示.

表1 单元折痕方案

2.2 有限元方法验证

采用Zhou等[26]的拟静力试验数据对运用有限元软件ANSYS 18.0进行数值模拟的有效性进行验证.Zhou等[26]对如图3所示的基于crash box构形的折纸管进行了拟静力轴向压溃试验,图中,b=60 mm,c=30 mm,h=58.7 mm.加载方向竖直向下,示意图如图4所示.模型采用板厚为1 mm的Q235钢材,钢材经过800 ℃退火处理以减少制作过程中冲压和焊接造成的残余应力.

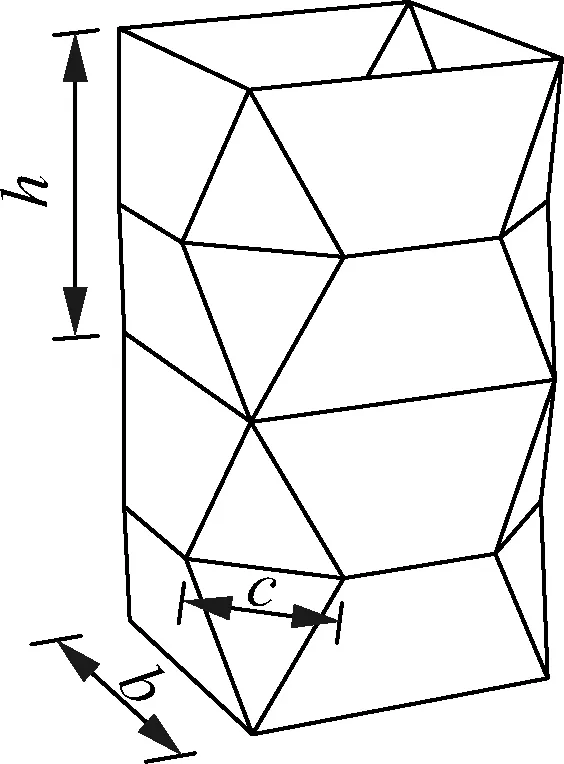
图3 Crash box折纸管

图4 试验加载示意图

采用有限元软件ANSYS/Implicit 18.0对试件的压溃试验进行数值模拟,材料本构采用文献[26]中的实测数据,有限元模型及其建模方法如图5所示.采用标准4节点壳元SHELL181来模拟折纸面板、刚性加载端头和刚性承压端.采用CONTA175单元和TARGE170单元分别对刚性加载端头表面和折纸管上端截面进行划分形成接触对,目标面的Pilot node设置在刚性加载端头的几何中心位置,通过该Pilot node施加荷载和边界约束.刚性承压端和折纸管下端截面采用相同的设置方法.刚性加载端只能沿管轴向平动(即XU=ZU=XROT=YROT=ZROT=0),刚性承压端则完全固定(即XU=YU=ZU=XROT=YROT=ZROT=0).

图5 有限元模型和建模方法

图6给出了轴向压力-加载位移(F0-Δ0)曲线的比较结果,可以看出试验值和模拟值的趋势大体一致；但两者的初始刚度有较为明显的差异.其原因在于试件的端部截面并不平整,试验初期加载端头和试件端部截面之间是逐步达到充分接触状态的；而数值模拟时,加载端头刚开始就和试件端部截面充分接触,一经加载即获得较大刚度.图7比较了试验和数值模拟得到的变形和应变分布,最大应力均发生在试件的尖点处(见图中红色虚线框),由于有4条峰线折痕在该点处相交,该点处出现了明显的应力集中,其余部位的变形和应变都吻合得较好.从以上比较可知,采用ANSYS/Implicit对折纸管进行模拟能够提供有效且可信的计算结果.

图6 轴向压力-加载位移(F0-Δ0)曲线

2.3 有限元建模

基于变角度Miura构形的折纸管是由3个如图2所示的管状折纸单元沿竖向堆叠而成.依照表1中的4种折痕方案形成4根折纸管，折纸管C-ORI-1、C-ORI-2、C-ORI-3和C-ORI-4分别采用折痕方案Ⅰ、Ⅱ、Ⅲ和Ⅳ.在闭合条件式(1)的约束下，为保证各折纸管只是折痕方案不同而其几何拓扑相同，各折纸管采用完全相同的几何参数设置，即H=200 mm，l=l1+l2=200 mm，φ1=85°,α=135°.

(a) 变形和最大主应变分布试验结果[26]

运用ANSYS/Implicit 18.0对基于变角度Miura构形的折纸管进行非线性分析,以考察各折纸管在轴心压力作用下的抗屈曲能力.折纸管的几何模型和有限元模型如图8所示.采用标准4节点壳元SHELL181来模拟8 mm厚的折纸面板和20 mm厚的管端封板.采用点元MASS21通过刚性梁元MPC184连接封板节点的方法来实现管端部绕MASS21单元的整体刚性转动,以模拟管两端与边界的铰接连接.外荷载和支座反力均通过MASS21单元施加和传递,加载端MASS21单元只能沿管轴向平动和绕X、Y轴转动(即XU=YU=ZROT=0),支座端MASS21单元只能绕X、Y轴转动(即XU=YU=ZU=ZROT=0).通过耦合节点平动自由度的方法来简化模拟A类折痕.模型材料采用钢材Q235B,其本构关系采用考虑强化段的基于钢材连续屈服理论的四折线模型[27],如图9所示,相关力学参数见表2,其中fy、fu分别为材料屈服强度和极限强度,E和Est分别为材料弹性模量和强化模量,εy、εst、εu和εel分别为材料屈服应变、强化应变、极限强度对应应变和极限应变.为保证轴心压力作用下折纸管达到其极限承载能力,有限元模拟时采用位移加载,加载位移取60 mm(约为构件计算长度的5.4%).

(a) 几何模型

图9 材料本构关系

表2 材料本构关系的参数设置

2.4 计算结果和讨论

图10 折纸管的荷载F-加载位移Δ曲线

(2)

(3)

式中,l0为折纸管的计算长度,l0=1 119 mm;t为折纸面板厚度,t=8 mm.各曲线的荷载峰值点用十字形进行标记，各荷载峰值点对应的达到荷载峰值时的加载位移Δpeak和其对应的平均轴向应变εpeak分别列入表3中.各折纸管在荷载达到峰值时和加载结束(Δ=60 mm)时的Von Mises应力状态分别如图11和图12所示.由图可见,各折纸管的应力和变形状态在数值、分布和形态上很相似,最大应力均出现在构件中部的顶点和B类折痕附近.达到荷载峰值时折纸管的侧向弯曲程度并不明显.相比较而言,加载结束(Δ=60 mm)时折纸管的整体屈曲程度则要显著得多.由上述分析可以发现,受压过程中各折纸管的变形模式遵循相同的变化规律:在达到荷载峰值点之前,各折纸管的变形由轴向压缩控制,仅产生略微的整体弯曲屈曲;达到荷载峰值点后,各折纸管整体屈曲显著增大,变形模式由轴向压缩控制转变为整体弯曲屈曲控制,并伴随承载能力的明显下降,构件发生失稳.从表3中也可以发现,折纸管C-ORI-4达到荷载峰值时的加载位移Δpeak和其对应的平均轴向应变εpeak明显大于其他折纸管,大约是其余折纸管的1.3～1.4倍,这表明该构件具有更加优越的轴向变形能力.

(a) C-ORI-1

通过模拟结果可以发现,与典型的两端简支轴心受压构件一致,折纸管的整体弯曲屈曲呈半波状.因此,折纸管端部绕支座的转角与其侧向挠度幅值呈正相关(见图13),此处用该转角来表征折纸管发生整体弯曲的程度.图14给出了加载过程中各折纸管端部转角θ随加载位移Δ的变化曲线,其中加载端转角为θtop,支座端转角为θbot,转角方向以顺时针为正,故θ=0以上部分表示θtop的变化趋势，θ=0以下部分表示θbot的变化趋势.折纸管C-ORI-4达到荷载峰值的时刻在图中用虚线表示，其余构件达到荷载峰值的时刻范围在图中用粉红色区域表示.从图中可看到,相同加载位移Δ下,转角θtop和θbot的大小基本相同,说明折纸管上下部分的整体弯曲较为均匀.在变形由整体屈曲变形控制(即达到荷载峰值)前转角θ均较小且几乎随加载位移Δ线性增长,而在变形由整体屈曲变形控制后转角θ的增长明显加快,表现出明显的非线性.对比各折纸管,折纸管C-ORI-4在整个加载过程中转角最小.对应于相同的加载位移Δ,折纸管C-ORI-4的转角分别为折纸管C-ORI-1、C-ORI-2和C-ORI-3转角的40.1%、42.7%和47.7%,使折纸管的侧向弯曲至少降低了52.3%,同时最大转角仅为6.5°,该现象表明折纸管C-ORI-4发生整体弯曲屈曲的程度最小.

图13 转角θ的示意图

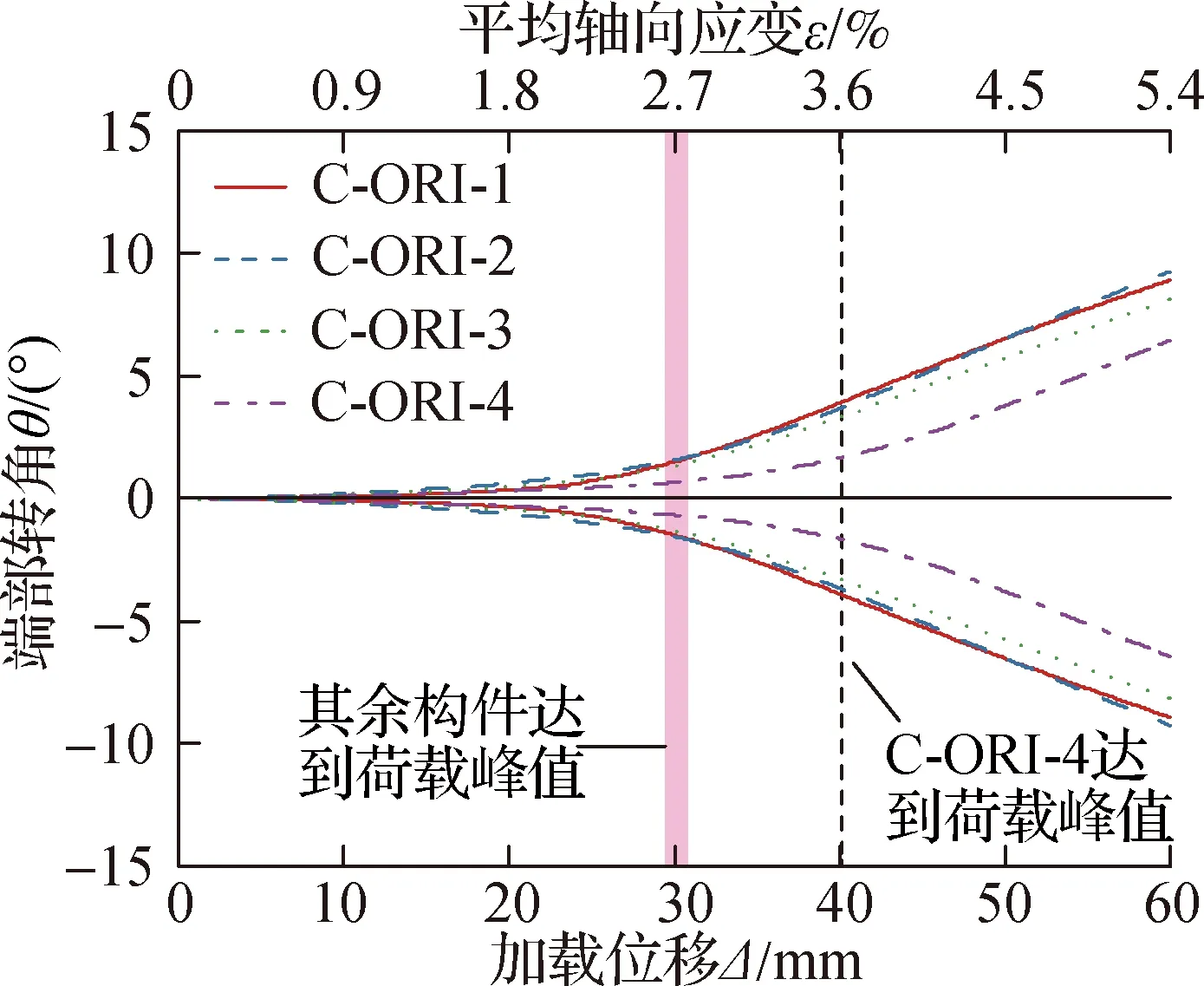
图14 折纸管端部转角θ随加载位移Δ的变化曲线

通过以上计算结果和分析发现，在本文研究的折纸管中，与其余构件相比，折纸管C-ORI-4的侧向弯曲减小了52.3%，同时发生整体屈曲的时刻延迟了38.5%，折纸管C-ORI-4具有最优越的抗屈曲能力.由于各折纸管具有相同的几何拓扑，折纸管C-ORI-4所代表的折痕方案Ⅳ(将斜向谷线折痕设置为完美铰折痕、其余折痕设置为连续折痕)是增强基于变角度Miura构形折纸管抗屈曲能力的最有效折痕方案.