黄土取土方向微观分析与动三轴颗粒流模拟研究

邓 津 安 亮 王盛年

(1兰州地球物理国家野外科学观测研究站, 兰州 730000)(2中国地震局兰州岩土地震研究所, 兰州 730000)(3甘肃省交通规划勘察设计院有限责任公司, 兰州 730030)(4南京工业大学交通运输工程学院, 南京 211816)

宏微观土力学是21世纪岩土工程重要研究方向[1].在自然沉积条件下,不同沉积环境下的微观结构差别很大,其颗粒组成、形状系数、孔隙分布、排列方式等均有差异,导致动应力-应变曲线和动力学性质也有明显区别[2-4].原状非饱和黄土试验包括常规土工室内试验、土动力学试验、离心模型试验等[5].通过黄土动三轴和共振柱等动力试验,可获得动强度和动应力-应变关系,计算动孔压特性曲线,用于筑坝黄土工程测试[6].动三轴试验结果表明,黄土的含水量、孔隙比、试验振次、固结应力比等关键参量对黄土震陷变形有较大影响[7].西宁、兰州、西吉、西安等地原状黄土的动强度特性研究表明,原状黄土黏粒含量基本呈自西北向东南增大趋势,动黏聚力也逐渐增大,内摩擦角呈减小的趋势,但幅值减小不具有相似性[8].黄土地区原状黄土的动力学性质也有较大的差异,主要表现在动弹性模量降低和残余变形(震陷系数)明显增大.

由于西北黄土是在寒冷干燥且近沙源地区形成,砂粒沉积堆积速度快,胶结黏粒少,微结构照片能记录成土信息和反应结构强度[9].从高倍电子显微镜下获取的微观结构照片中可以获取土的颗粒信息,如颗粒形状系数、长轴、短轴、角度等,便于开展微观参数定量化研究[10-13].PFC颗粒流离散单元法推动了宏微观土力学研究方向的加速发展,采用颗粒流法能模拟土颗粒在动荷载作用下的变化过程.例如,利用颗粒流法模拟二维颗粒数目及孔隙率,可获得转换公式[14-15].利用重力沉积法可建立不规则砂土颗粒单元平面双轴试验模型,进而分析砂土试样表现出的宏观原生各向异性力学特性与内部颗粒结构的关系[16].利用颗粒流方法研究围压与动剪应力比对粉土崩塌特性的影响[17]等.此外,颗粒不规则形状的选取也是颗粒流模拟的重点之一[18-19].黄土微观结构与环境及微观土动力学分析逐渐得到重视;颗粒流模拟土力学性质和试验分析及滑坡场地分析计算获得较广泛的应用[20-25].

本文选择平行于沉积方向和垂直于沉积方向对土样进行动三轴试验,考虑微观参数中颗粒形状和实际粒径大小等参数,进行PFC颗粒流模拟,建立近似的黄土微观颗粒模型,从而精细拟合动应力-应变关系曲线,研究取土方向的微观差别与土动力学各向异性.

1 取样截面分析

选取兰州新区地下4 m原状土样3号样进行分析,考虑到不同取样方向可能导致微观结构差异,采用4个截面分析微观差别.设垂直于沉积方向的2个面为h面,平行于沉积方向的为s面.如图1所示,取样方式包括:① 沉积方向竖向取样(3s-s);② 垂直于沉积方向横向取样(3h-h);③ 竖向加载时采用沉积方向面3s-s作为加载测试面,受力接触面为3s-h;④ 横向加载时以垂直于沉积方向的3h-h面为加载测试面,受力接触面为3h-s.四个截面分别为横向取土面3h-s和3h-h,以及竖向取土面3s-s,3s-h.试验采用2种加载方式(横向加载和竖向加载)测试土的动三轴应力-应变曲线并进行颗粒流模拟.

图1 兰州黄土土样4种取样方式示意图

2 动三轴试验

对该样品在偏压固结下进行不排水动三轴试验,所加动荷载为频率1 Hz的正弦波.在静压力σ1C(轴向压力)和σ3C(侧向压力)下固结,加载压力比K0=0.59.待固结稳定后,沿轴向逐级持续施加动应力,土样产生较大变形后,停止施加动应力.选取沉积向取土样和横向取土样2种方式,获得2组动应力-应变曲线.横向及竖向加载的动三轴动应力-应变曲线见图2.如图所示,3s-s和3h-h截面试验曲线分别在0.3%和0.4%应变时达到非线性段转折点,曲线由弹塑性平缓段到快速增大,直到土样破坏.采用颗粒流拟合得到4个截面的动应力-应变计算曲线,如图2所示.

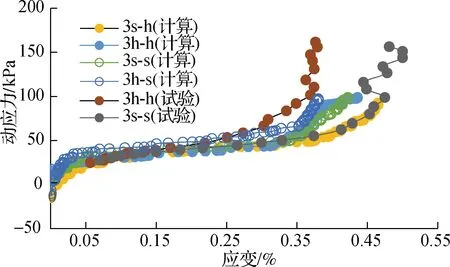
图2 动三轴试验曲线与PFC计算曲线

3 颗粒流拟合

3.1 微观参数提取

对4个取样截面进行微观电镜分析,仪器选用KyKy-2800BSEM型高倍电子显微镜(北京中科生仪科技有限公司).放大倍数为500,微观电镜照片如图3(a)～(d)所示.由图可见,4个截面的颗粒排列均不同:3s-s截面的颗粒较大,架空孔隙堆积结构;3h-h截面为大颗粒中填充有很多小颗粒,明显比3s-s截面更致密;3s-h截面含有更多小颗粒且分布较为均匀,孔隙较少;3h-s截面则兼具架空大颗粒和小颗粒,它们胶结分布在大颗粒周边.

(a) 3h-h截面

采用PCAS图像灰度处理软件分析微观电镜照片,描出颗粒边界,提取获得4个截面的微观数据[13-14].如图3(e)～(h)和表1所示,3s-s的颗粒体积分数和平均长轴粒径最大,为75.09%和48.88 μm;3h-h截面的颗粒体积分数和平均长轴粒径最小,分别为63.71%和31.72 μm.两者形状系数分别为0.425 2和0.348 3.而3h-s和3s-h截面介于两者之间,形状系数分别为0.415 4和0.360 3,平均长轴粒径分别为36.67和37.08 μm,颗粒体积分数分别为65.74%和63.97%.可见4个截面颗粒的平均长轴粒径、形状系数以及颗粒含量、曲率系数等各类指标参数均有明显差别,如图4(a)～(d)所示.

表1 4个截面电镜微观指标

形状系数定义为等价圆周长与真实周长的比值,形状系数曲线越平缓,颗粒越接近圆形.颗粒形状介于矩形和圆形之间,因此颗粒形状系数取值范围为0.3～1.四个方向颗粒形状系数曲线如图4(a)所示,其中3s-s截面的形状系数曲线更加陡峭,3s-h截面的形状系数曲线最为平缓,因此其颗粒形状较接近于圆形.

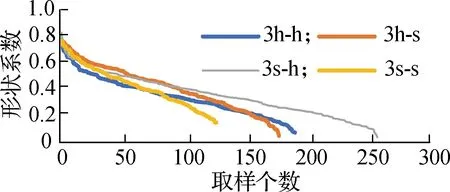
(a) 形状系数

长轴粒径分布如图4(b)所示,3h-s、3h-h、3s-h和3s-s 四个截面微观颗粒0～25 μm粒径含量(体积分数)分别为 50.28%、44.74%、43.19%、40.94%,可见粒径组成相差较大.

颗粒角度差别也导致颗粒在加载过程中产生位移的力链位置和试验曲线均不同.长轴角度分布如图4(c)和(d)所示, 3s-h截面的长轴角度曲线比3s-s截面更加平缓, 最平缓的为3s-s截面.3s-s和3h-h截面的角度频率分布曲线峰值均在20°左右;3s-h和3h-s截面的角度分布曲线有多个峰值,为20°、40°、60°、80°、180°.

颗粒长轴粒径及角度的玫瑰图如图5(a)～(d)所示.容易变形的颗粒角度分布在50°～100°范围的长轴粒径大小差别较大:3s-s截面集中在33～45 μm;3s-h截面集中在14～15 μm;3h-s 截面集中在25～35 μm,角度80～140°.3h-h、3s-h和3s-s截面的粒径均值分别为12、15、23 μm.

(a) 3s-s截面

3.2 颗粒流参数选取

通过PCAS软件处理4个截面的电镜数据,颗粒长轴粒径b按25～40、40～55、55～70、70～85、85～120 μm的区间进行粒径分组,如表2所示.由于25 μm以下颗粒作为胶结物考虑,因此没有计算在内.颗粒流模拟时考虑到颗粒长轴及角度的差异,计算得到的刚度及刚度比(计算方法见文献[26])如表2所示.图6(a)～(d)为利用PFC软件流获取的4个截面的模型图,加载前4个截面颗粒为随机排列方式.在PFC离散元数值模拟时考虑到土颗粒真实形状,采用长方形不规则集合颗粒(clump)模拟土颗粒,该方法可近似模拟土颗粒的长轴和长轴角度.

(a) 3h-h截面

表2 4个方向截面颗粒流模拟参数

图6(e)给出了4个截面的粒径按照高倍电镜获取的微观颗粒粒径含量的分组(左侧)以及颗粒流计算得到的颗粒粒径含量分组(右侧),两者基本接近.

3.3 颗粒流模拟动应力-应变曲线

采用PFC重力沉积法和不规则砂土颗粒平面双轴试验模型，对不同加载时刻下不同截面分别进行颗粒流模拟.首先在水平和竖直方向上施加固结荷载(本文选取60 kPa),得到类似沉积条件下的土样.模拟采用应变加载,给墙体施加速度,加载速度为0.01 m/s,获得试样宏观应力-应变曲线.

将采用PFC颗粒流模拟获得的4个截面的动应力-应变拟合曲线(见图2)与2条试验曲线对比发现,拟合曲线接近试验曲线,在弹性阶段拟合较好,并且在非线性阶段拟合曲线变化趋势与试验数据接近.

4 动应力-应变过程颗粒流分析

颗粒计算过程分析包括颗粒位移产生方式和力链的变化,动应力-应变曲线阶段变化与颗粒运动.

4.1 颗粒位移速度和力链

图7为3s-h截面不同应变下的颗粒位移分布图,试样加载前颗粒是随机排列的.加载后,颗粒产生定向位移,颜色越浅,颗粒的滑动位移越大.固结后产生明显的滑移面,颗粒定向排列,中间有较大位移集中面(约35°).1%和2%的应变后产生多个大小不同的剪切面(30°～60°),4%和5%应变后的颗粒位移均集中在试样中部,这符合实际三轴试验后样品中间突出的现象.

(a) 预加载

图8为3h-h截面颗粒位移速度示意图.图中箭头表示颗粒速度大小及方向,加载前箭头是杂乱分布的,1%应变之后箭头排列定向性明显,2%应变时箭头在中部位移最大,3%应变后位移鼓包集中在2/3处.

(a) 加载前

因此，颗粒发生定向位移是产生应变的原因.加载后只在特定的部位产生颗粒的定向位移,并集中产生定向剪切面.

4.2 应力集中位置变化

颗粒流计算应变过程中颗粒位移及力链变化如图9所示.加载前力链没有形成连线,如图9(a)所示.图9(b)、(c) 为3h-h截面在5%应变下的颗粒位移及力链变化图, 图9(d)、(e)为3s-s截面在5%应变下的颗粒位移及力链变化图, 图9(f)、(g)为3s-h截面在5%应变下的颗粒位移及力链变化图.由图可见: 3个截面力链和应力集中位置不同,3h-h位移集中在上下约1/3处的2个位置,力链接触点联线与中小颗粒连线接近;3s-s在右边出现上下两个应力集中区域;3s-h颗粒排列不均匀,在中间左右两侧形成不均匀受力鼓包,力链包线间隔较小.因此,颗粒力链形成与原始的颗粒排列有关.由于颗粒的排列和粒径分布的差异,力链产生的方向和位置也在发生变化.受力点连在一起形成颗粒剪切滑动面.小颗粒连线易于形成剪切力链,变形小;大颗粒接触点所形成的力链包线间隔较大,变形也大.

(a) 3h-h原状力链

4.3 动应力-应变曲线变化

图10为3s-h、3h-s、3h-h、3s-s四个截面在设定5%应变下动应力-应变曲线与颗粒位移的变化示意图.在同样的应变下,应力最大峰值明显不同,即在同一个加载应变下,动应力-应变曲线形状也发生变化,同时土样4个截面颗粒位移的位置不同.因此,动应力-应变峰值变化也是由于颗粒排列差异导致的.

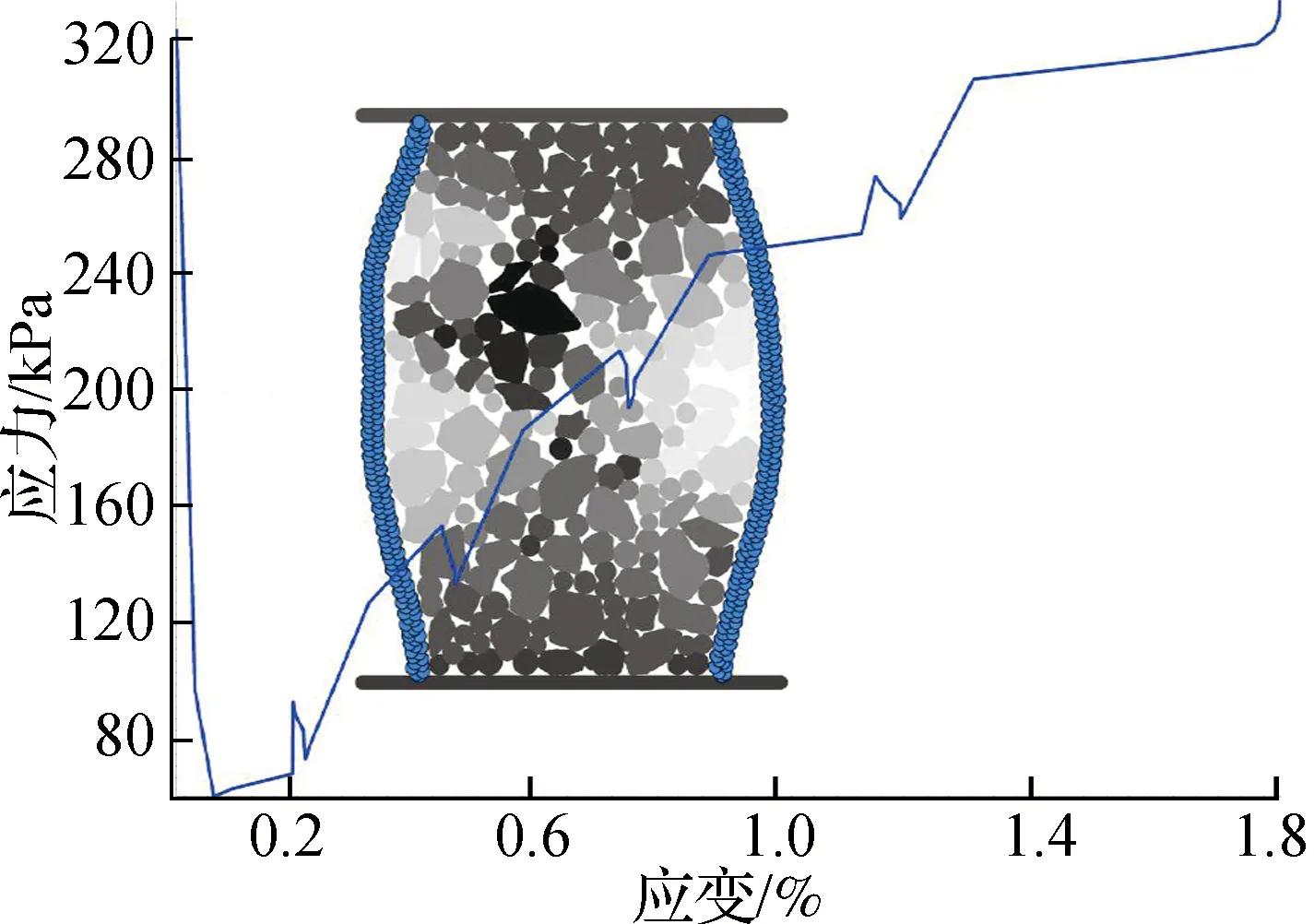
(a) 3h-s截面

4.4 不平衡力变化

截面3s-s在固结和加载过程中变形达到0%、2%、4%、6%时的不平衡力变化如图11(a)～(d)所示.固结时的应变小于0.8×10-2；2%变形下，最大应变2.2×10-2，应力200 kPa；4%变形下，最大应变3.5×10-2，应力260 kPa；6%变形下，曲线达到应力应变峰值，最大应变达到0.14，应力380 kPa.由图11可见,在颗粒接触点之间形成不平衡力,最大不平衡力并不集中在所有颗粒上,或是在某些大颗粒上,而是集中在支架接触点连线或大小颗粒悬殊的特定颗粒接触点上,最终导致不同截面形变位置发生差异.

(a) 固结0%

综上所述,不同取土地点会造成微观差异,甚至同一样品选择不同方向的沉积面也会造成差别.由于颗粒粒径分布及方向均不同并且颗粒随机分布,颗粒流模拟的动应力-应变曲线也有明显的差别,表明了黄土各向异性产生的结构性原因.

5 结论

1) 本文通过研究兰州新区地下4 m土样,分析不同沉积方向4个截面的微观颗粒指标,发现不同截面的微观参数(颗粒长轴粒径及角度)及颗粒排列均有较大差别.同时动三轴试验获取的动应力-应变曲线形状与颗粒位移变化相差很大,表现了黄土各向异性结构特征.

2) 采用4个截面的微观颗粒参数以及合理的刚度和刚度比,进行PFC颗粒流模拟,得到的动应力-应变曲线接近动三轴试验曲线,体现了黄土微观差异导致的曲线细节差别.由于颗粒长轴分组以及排列方向差异,导致不同截面剪切破裂带和力链位置方向均不同,剪切面差别较大,最终动应力-应变曲线峰值及形状均存在差异.因此,土颗粒参数和排列方式差别是产生动力学曲线差异的重要原因之一.

3) 采用宏微观相结合的分析方法,将微观颗粒参数差异分析及颗粒流计算方法相结合,能有效地获取动应力-应变曲线.该方法也可用于不同深度土样土层剖面的非线性动应力-应变试验曲线模拟,以及土层动力分析及地震工程学计算等.