概率统计法测算非饱和土渗透系数的理论研究

朱益瑶 翟 钱

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)(东南大学土木工程学院, 南京211189)

在岩土工程领域，充分了解土体的水力特性对工程的设计、施工及安全监测都有着至关重要的指导性意义.工程中遇到的土大多位于地下水位之上，处于非饱和状态.在工程实际中，石油在地下环境中的存储、垃圾填埋场废液和废气的运移分析、高放废物地下处置填充材料的设计等都需要对非饱和土的水渗流特性进行考虑[1].因此，渗透系数的确定对非饱和土性质研究十分重要.非饱和土中，孔隙水的分布及其含量变化对土体的工程性质有着显著影响[2]，土体中水力路径的微观变化会引起非饱和土宏观上力学和水力行为的不同响应，当土体饱和度随环境不断变化时，其渗透系数及强度也会发生相应的改变[3].本文将在不同饱和度条件下，讨论土体内部的孔隙水分布及其有效渗流面积，并以此为基础对土体的相对渗透系数进行测算.

渗透系数一般可通过2种方法获得，即直接的实验测量法和间接的估算法.非饱和土渗透系数试验测量难度较大，即使是在近饱和状态，由微小的吸力变化而引起的渗透系数改变也可达1～3 个数量级[4]，且测量过程较为费时，费用也很高昂.与直接测量的方法相比，间接计算的方法具有便捷性和经济性的显著优势.在非饱和土力学理论发展完善的过程中，研究人员提出了许多非饱和土渗透系数的间接计算模型，Mualem[5]将这些间接计算方法分为3类：经验模型、宏观模型和统计模型.其中统计模型被认为是最严谨和精确的计算方法[6].因此，利用数学模型估算非饱和土渗透系数的方法在工程实践中得到越来越多的应用.在Childs等[7]提出的渗流物理模型基础上，Fredlund等[8]利用土水特征曲线(SWCC)提出了非饱和土渗透系数的积分形式计算式；孙大松等[9]通过建立土中孔隙的分形模型，推导得到了渗透系数表达式；蔡国庆等[10]基于Mualem 模型，在不同初始孔隙比条件下对相对渗透系数进行了预测；Zhai等[11]提出用概率统计的方法计算土体截面上的有效渗流面积,再通过面积比来测算非饱和土的相对渗透系数；邵龙潭等[12]利用孔隙水的微分平衡方程，推导得到了渗透系数计算式.

在众多非饱和土渗透系数的计算模型中，Fredlund等[13]推荐采用Zhai等[11]模型计算非饱和土的渗透系数，认为其不仅可直接简便地用EXCEL进行计算，而且对具有双峰SWCC的材料也能进行很好的测算.但Zhai等[11]在介绍基本原理后直接给出公式，未对公式进行严格推导.基于此，本文将对此公式的理论进行详尽阐述，并用概率统计的方法对公式进行严谨推导.最后，采用数学推导的方式，将该公式与Fredlund等[8]提出的积分形式渗透系数计算式进行对比，从本质上分析其一致性.

1 理论推导

1.1 土水特征曲线与孔径分布函数关系

SWCC主要反映了土体含水量随基质吸力变化的关系.通过SWCC的曲线形态分析及特征参数(进气值、残余吸力、残余含水量等)计算，可对非饱和土的工程性质进行推算和估计[14].一维渗流分析中，常采用一系列平行于渗流方向的毛细管来代替土体单元截面上不规则的孔隙[15].由毛细定律可知，ψi=2T/ri,即任一吸力都对应于一个毛细孔隙半径.式中,ri为毛细管半径，mm；ψi为基质吸力，kPa；T为一个与环境有关的常数.因此，可将土体截面上任意形状的孔隙简化为对应于不同吸力的一系列圆孔(见图1).

图1 土截面不规则孔隙的简化

在土体排水过程中，基质吸力ψ不断增大.当基质吸力由ψi增大至ψi+Δψ时，ri至ri-Δr孔隙中的水被排出，且排出水体积与该范围孔隙体积相等.故当基质吸力为ψi时，仅小于等于ri的孔隙中含水.令孔隙总体积为单位1，饱和度Si在数值上与r≤ri的孔隙密度之和相等，因此可得到SWCC与孔径分布函数(PSDF)的关系如图2所示，其中f(ψ)为毛细定律下基质吸力ψ所对应的孔径密度.

图2 SWCC与PSDF关系示意图

1.2 特征孔隙半径及孔隙密度确定

利用SWCC计算非饱和土渗透系数时，等效孔隙半径及孔隙密度的确定取决于该曲线的划分方式.统计模型中，区间划分的方式主要有2种：①含水量区间等间距划分[16]；②基质吸力区间等间距划分[11].第1种方法中，基质吸力的变化量Δψ及其对应的孔隙半径变化区间Δr，需要由SWCC上含水量变化值Δθ进行推算.由SWCC的曲线形态分析可知，含水量在基质吸力较低和较高范围的变化率都较小.因此，较低和较高吸力范围的分区数量较少，数据点主要集中于中间区域.该方法仅适用于单峰SWCC，对双峰SWCC的应用存在局限性.基质吸力区间等分的方法能有效避免这些缺陷.将SWCC在基质吸力范围等分，当分组足够多 (≥40组) 时，采用区间内任一半径作为该组的特征孔隙半径，对渗透系数总体计算精度的影响可忽略不计[17].本文将采用等分基质吸力区间的方法，对土体中的孔隙进行分组，并选择每一区间的左端点作为该组孔隙的特征孔隙半径r，利用其所对应的孔隙密度f(r)，进行非饱和土相对渗透系数的推算.

1.3 饱和状态下的有效渗流面积

不考虑土体体积变化时，饱和土的渗透系数恒定不变.在饱和土横截面上，仅存在饱和孔隙和土颗粒2种单元，仅当孔隙与孔隙连接时，水流才能顺利通过土体截面.对于同一土样，各截面的PSDF相同，即每一截面上不同大小的孔隙所占比例相同且随机分布.因此，可仅对某一截面进行讨论，由该截面的有效渗流面积代替土体整体的有效渗流面积.由孔隙率n的定义可知，其代表土体孔隙体积与总体积之比.对于某一截面，孔隙率n可理解为该面上的孔隙面积与总面积之比.在SWCC上，沿着基质吸力增大的方向，截面上的孔隙可按其特征半径，由大到小分为N组(r1>r2>r3>…>rN).对于孔径在区间[ri0,ri1)内的孔隙，可取ri0作为特征孔隙半径.各组孔隙密度与饱和度关系如图3所示，每一组孔隙所对应的孔隙密度为

图3 孔隙密度与饱和度关系

Si0-Si1=ΔSii=1,2,…,N

对于土体上的相邻两截面1、2，可将土颗粒视为上述统计模型中的黑球，孔隙视为白球.在每一面上，选中孔隙的概率等于孔隙面积与截面总面积之比n.同时，该选中孔隙半径为ri的概率等于孔隙ri的孔隙密度f(ri)，故在该饱和土截面上选中孔隙ri的概率Pi=nf(ri).已知在截面1和截面2上，各孔隙具有相同的密度，且随机连接，则截面1上的孔隙ri与截面2上的孔隙rj相连的概率Pi,j=n2f(rj)f(ri).

A(ri,rj)=

(1)

计算由孔隙ri决定的有效渗流面积时，ri可能位于截面1，也可能位于截面2.以概率为权重，对2个截面上不同孔隙组合的渗流面积加权累和，计算可得

(2)

取各区间左端对应的孔隙半径为特征孔隙半径，即

S(ψ1)=1

由此可得

(3)

式中，S(ψ1)、S(ψi)、S(ψi+1)分别为SWCC上基质吸力ψ1、ψi和ψi+1对应的饱和度.

将所有由不同孔隙决定的有效渗流面积相加，可得到饱和状态下土体的有效渗流面积As,即

(4)

1.4 非饱和状态下有效渗流面积

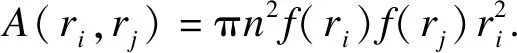
(5)

式中,i,j=1,2,…,N.

计算由ri确定的有效渗流面积时，ri可能位于截面1，也可能位于截面2，将所有可能的情况相加，得

A(ri)=[2f(rk)f(ri)+2f(rk+1)f(ri)+

2f(rk+2)f(ri)+…+2f(ri-1)f(ri)+f(ri)f(ri)]·

(6)

由SWCC与PSDF关系分析可得

因此，当基质吸力大小为ψk时，由ri决定的有效渗流面积之和为

A(ri)=[[S(ψk)-S(ψi+1)]2-

(7)

考虑所有的组合情况，将横截面上所有有效渗流面积相加，可得到基质吸力大小为ψk时非饱和土有效渗流面积之和Ak,即

(8)

1.5 相对渗透系数

在环境稳定且流体本身性质不变的条件下，液体和气体在土体中的渗流规律主要取决于土体中的孔隙几何分布情况[18].由泊肃叶定律可知，在单位面积上，流体在单位时间内的流量与流体的黏滞系数及流管两端压强差成正比.为避免由环境参数及液体本身性质参数在渗透系数的计算上引起计算误差，常采用相对渗透系数的方法，在已知饱和渗透系数的情况下，对非饱和土不同吸力条件下的渗透系数进行测算.Zhai等[15]通过对泊肃叶定律的分析发现，不饱和土的相对渗透系数与渗透面积成正比，据此提出了阀门模型，如图4所示，其中，s1∶s2∶s3=k1∶k2∶k3.

图4 阀门模型

基于阀门模型，可得到非饱和土的相对渗透系数计算式如下：

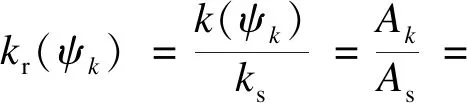
(9)

式中,kr(ψk)为基质吸力等于ψk时非饱和土的相对渗透系数.

利用毛细定律r=2T/ψ,式(9)可简化为仅与基质吸力ψ相关的函数，即

(10)

2 本文公式与已有公式对比

Fredlund等[8]基于Childs等[7]的渗流物理模型，提出了积分形式的非饱和土渗透系数计算式，即

(11)

式中，ψr为残余吸力，kPa；ψAEV为进气值,kPa；θ(ψ) 为基质吸力等于ψ时土的体积含水量.由定积分定义可知，积分式可化为自变量区间上的和式极限,式(11)的分子与分母可分别用累和的形式表达，即

(12)

由一阶泰勒展开可知

f(x+Δx)≈f(x)+f(x)′Δx

则θ′(ψi)(ψi+1-ψi)=θ(ψi+1)-θ(ψi) ，代入式(12)可得

(13)

对定积分上下限进行足够多的区间划分后，可忽略由泰勒展开省去的高阶导部分误差，则Fredlund等[8]提出的渗透系数计算式可转化为累和的形式：

kr(ψk)=

(14)

已知含水量θw与饱和度S之间存在关系θw=mS.在不考虑土体体积变形的情况下，m为常数，S(ψAEV)=1.故式(14)可进一步表达成饱和度形式：

kr(ψk)=

(15)

对于本文推导得到的式(10)，可利用平方差公式将其进一步改写为

(16)

当基质吸力被划分为足够多的区间时，S(ψi+1)与S(ψi)近似相等，此时有

2S(ψk)-S(ψi+1)-S(ψi)≈2[S(ψk)-S(ψi)]

2-S(ψi+1)-S(ψi)≈2[1-S(ψi)]

将其代入式(16)得

(17)

此时，式(17)与式(15)是相等的.因此，不考虑土体体积变形，并将SWCC划分得足够细时，本文公式与Fredlund等[8]提出的式(11)在本质上是一致的.在Fredlund等[8]的公式中，需要采用体积含水量对基质吸力求一阶导数，然后再进行积分运算，计算过程复杂，很大程度上依赖于计算机程序.相比之下，本文公式仅需EXCEL表格，便可对渗透系数进行较高精度的测算.

3 结论

1) 本文基于毛细定律，详细阐述了SWCC与PSDF的关系.采用概率统计的方法，从理论上详细推导得到了非饱和土相对渗透系数的计算式，将其作为Zhai等公式的拓展与补充.

2) 通过理论推导，证明当吸力范围被划分得足够细且忽略土体体积变化时，本文公式与Fredlund等提出的非饱和土渗透系数计算式在本质上是一致的，且本文公式更适合在工程实践中普及应用.

3) 土体体积发生变化时，孔隙之间连接的概率将发生变化，其有效渗流面积的计算结果也会随之改变.因此，在考虑土体体积变化时，需对采用概率统计法计算的非饱和土渗透系数作进一步的修正和讨论.