传染病传播的动力学分析与数值模拟
2021-10-21唐雄
唐 雄
(数学与统计学院黄淮学院,河南 驻马店463000)
0 引言
一直以来,有许多从事生物数学研究的工作是利用数学建模的手段来探讨传染病的传播机理和评价不同控制措施的控制效果。经过多年的研究,逐步提出了根据传染病传播机理所建立的SIR等较为复杂的模型。
1 SIR模型及其动力学分析
1.1 模型的建立
SIR模型广泛地运用于传染病的传播动力学的研究上,比如,天花、肝炎等传染病。为了便于建立相应的数学模型,做如下假设和符号说明:(1)假定传染病在整个传播周期内整个人口的数量不变,即人口的出生率和死亡率相等;(2)易感者和感染者的接触采用双线性发生率;(3)不考虑因病的死亡;(4)整个人群分为易感者S(t)、感染者I(t)和康复者R(t)。因此可以建立如下具有指数出生和指数死亡的SIR模型:
不难推出模型(2)存在如下一个正不变集(S,I)∈D{(S,I)|0≤S≤N,0≤I≤N,0≤S+I≤N}。
由此,可以得到传染病的基本再生数为R0=
1.2 对模型(2)的动力学分析
下面将探讨模型(2)的动力学行为,并且得到使得传染病消失的充分条件。
定理1:当R0<1时,无病平衡点E0(N,0)是全局稳定的。
定理2:当R0>1时,地方病平衡点E1是全局稳定。
由定理1和定理2可知,当比本再生数R0<1时传染病可以得到有效地控制。进一步来说,从R0的表达式可以看出,减少接触率和增大治愈率是控制传染病的重要的手段。
1.3 具有疫苗接种SIR模型的动力学分析
下面探讨免疫疫苗接种对传染病传播的影响,建立具有免疫疫苗接种的传染病传播模型,模型如下:
其中μ是免疫接种率,可以得到模型(4)的前两个方程与R无关,对模型(4)的理论分析可以考虑如下约简模型:
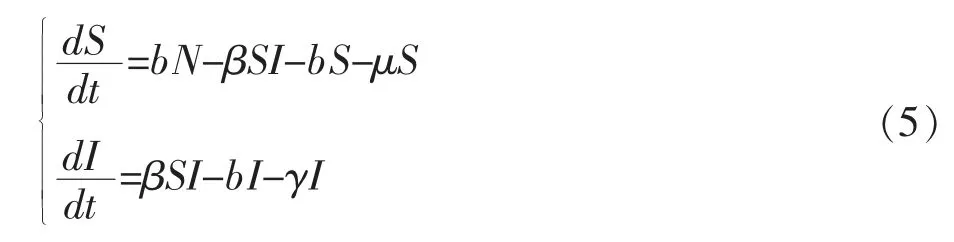
令模型(5)两个方程右端的等于0,可以得到模型(5)的两个平衡点分别为:无病平衡点总是存在的,当βNb<(b+γ)(b+μ)时存在地方病平衡点因此,在免疫疫苗接种的情况下,可以得到模型(4)的有效再生数为:
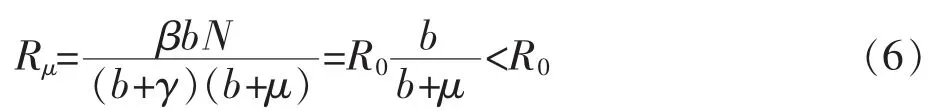
(6)式表明免疫疫苗接种是有利于控制传染病的传播的。于是可以得到如下定理:
定理3:当Rμ<1时,无病平衡点是全局稳定的。
定理4:当Rμ>1时,地方病平衡点E3是全局稳定的。
2 数值模拟及灵敏度分析
本节将通过数值模拟的方法,印证前面的理论分析。最后通过灵敏度分析来探讨哪些因素更容易控制传染病的传播。
2.1 数值模拟
从上面的相关讨论可知基本再生数R0与参数β,b和γ有关。在疫苗免疫接种的情况下,有效再生数Rμ是在疫苗免疫接种情况下传染病是否消失的阈值,有效再生数Rμ不但与参数β,b和γ有关,而且与疫苗免疫接种率μ有关。下面运用数值模拟来验证理论分析结果。考虑将一个具有100万人口的城市作为研究对象,即N=105。
(1)取b=4×10-3,β=2×10-6,λ=0.1,这时基本再生数R0=1.9231>1,由定理(2)可知,地方病平衡点是全局渐近稳定的。通过数值模拟可以看出,感染者数量随着时间的推移最终稳定到一个固定的值,形成一个稳定的地方病平衡点。
(2)取b=4×10-5,β=8×10-7,λ=0.1,这时基本再生数R0=0.769 2<1,从定理(1)可知,无病平衡点是全局渐近稳定的。通过数值模拟可以看出,感染者数量随着时间的推移最终趋于0,这也意味着传染病最终消失。
(3)取b=4×10-3,β=2×10-6,λ=0.1,这是基本再生数R0=1.923 1>1。从可以看出当μ*>(R0-1)b=0.0037时,Rμ<1。取μ=0.005,有Rμ=0.854 7<1,由定理3可知,无病平衡点是全局渐近稳定的。通过数值模拟可以看出当疫苗接种率大于阈值μ*时,传染病得到控制,并最终消失。
(4)取b=4×10-3,β=2×10-6,λ=0.1,这时基本再生数R0=1.923 1>1。取μ=0.002,此时Rμ=1.282 1>1,由定理4可知,地方病平衡点是全局渐近稳定的。
经过数值模拟可以发现感染者数量随着时间的推移最终趋于一个固定的值,这也意味着当疫苗接种率小于阈值μ*时,传染病并不能得到有效地控制。
2.2 灵敏度分析
下面通过对Rμ的灵敏度分析的方法探讨哪些因素更容易控制传染病的传播。固定N=105,μ=0.002和λ=0.1。由模拟后的结果可以看出Rμ随着有效接触率β的增加Rμ显著增加,这表明为了能够有效地控制传染病的传播,必须减少有效接触率。
固定N=105,b=4×10-3和β=2×10-6,由模拟后的结果可以看出Rμ随着疫苗接种率μ的增加而减少,说明提高疫苗的免疫接种率,可以达到群体免疫的效果。
3 结语
本文研究了SIR模型的动力学行为,探讨了平衡点的全局稳定性,得到使得传染病消除的条件。再则,研究了免疫疫苗接种对传染病传播的影响,得到了使得传染病消除的最低疫苗接种率,如果疫苗接种率高于该阈值传染病将最终消除。对于医护工作者来说要做好患者的隔离和护理,极大地提高患者的治愈率,减少患者与外界的接触是阻止疾病传播的重要手段。从数学的角度给出了传染病治疗的理论依据,印证了人类以往对付传染病时的手段和方法都是正确和有效的。
