DSPMVM电机的温升预测与研究

刘璟轩，李建贵，马 媛

（武汉理工大学机电工程学院，湖北 武汉430070）

1 引言

近几年，永磁游标电机的提出为低速大转矩应用场合提供了一个新的方案［1］。永磁游标电机在传统的永磁电机的基础上，充分运用“游标效应”，利用调制极调制电机磁路。游标效应是对电机定子电枢绕组产生的高速磁场进行谐波调制，获得可同具有高级对数的永磁体磁场相互作用的低速磁场。从而实现电机在低速运转情况下，得到更稳定更大地转矩输出。然而永磁游标电机的铁心与永磁体结构较为复杂，工作环境特殊，在设计阶段若不能考虑到温升等因素的影响，可能会导致一些严重的后果。永磁电机在工作中会产生各种热源损耗，进而产生温升。电机温升过高将导致铜线的绝缘层损坏、永磁体退磁或者定转子铁心损坏等问题。因此，在新型电机设计阶段必须充分考虑到电机温升的影响。

文献［2］中介绍了用于温度场预测的简化公式法，但是误差较大；文献［3］基于热路法完成了对异步电机定子铁心的温度场计算，但是并未对电机整体温度场进行研究；文献［4］利用热路法完成了对普锐斯2010款电动汽车电机的温度场研究，证明了热路法用于温度预测的有效性；文献［5］利用神经网络法建立目标电机的温升模型，达到准确预测电机温度的效果；文献［6-9］各自利用有限元法完成了对各电机磁热耦合温度场的计算过程。总体来说，有限元法因为计算准确，且利用软件仿真简便易行，所以使用广泛；热路法对目标电机建立数学模型与等效热路，计算结果准确度高，但需要大量计算节点热阻热容等参数；神经网络法等结合智能算法的预测方法较为复杂，需要硬件等在线支持。

结合上述优缺点，提出了一种新型双定子永磁游标电机（Double Stator Permanent Magnet Vernier Motor，DSPMVM）拓扑结构。首先，介绍了DSPMVM的结构特点与设计参数。其次，针对DSPMVM电机的工况进行选择，基于有限元电磁仿真，完成电机各部分热源损耗等参数的计算。再次，提出并搭建DSPMVM五热源等效热路模型对电机整体温度场进行仿真分析。最后，将电机各部分在几种工况下的温度与有限元法仿真计算的结果进行对比，证明利用等效热路法对DSPMVM电机温升计算的合理性，以及仿真结果的可靠性。

2 DSPMVM电机拓扑结构

以提出的一种新型DSPMVM电机为研究对象。该电机拓扑结构包含内、外双定子以及中间转子，是文献［10］所提出一种电机的变形结构。DSPMVM电机的部分主要设计参数已给出，如表1所示。

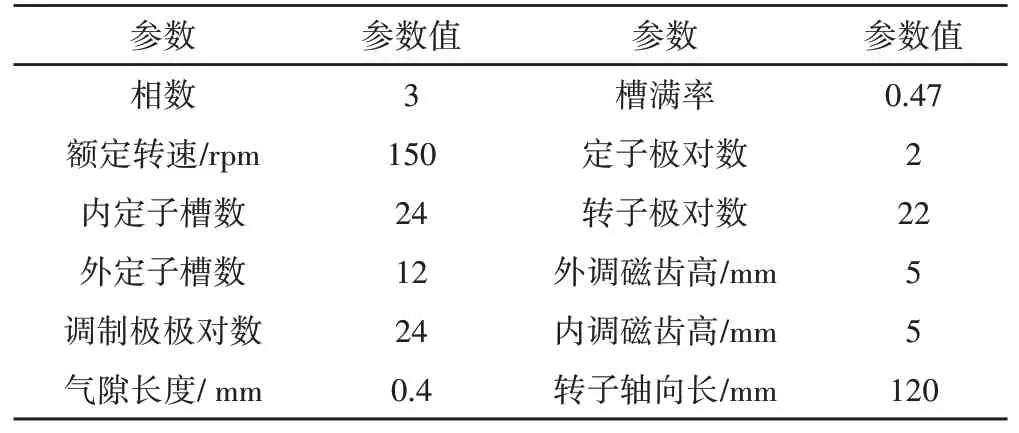
表1 新型DSPMVM的设计参数Tab.1 The Design Parameters of DSPMVM

该新型DSPMVM电机的二维模型，以及其内、外绕组各相电流的分布情况，如图1所示。永磁体采用内嵌的方式嵌入到转子内部，转子安装在内、外定子之间，从而可形成内外双层气隙磁场。该新型电机外定子在结构上采用Split-pole结构，不仅能大大节省电机制造材料，还增加了定子铁心的散热面积，一定程度上能缓解外定子局部过热情况发生；内定子采用Open-pole结构，其结构简单，能有效减小电机反电动势波形畸变率，保证电机电动势输出波形高度正弦化。另在内外定子上设计能够实现对DSPMVM内、外双层气隙磁场的磁通调制作用的调制极。

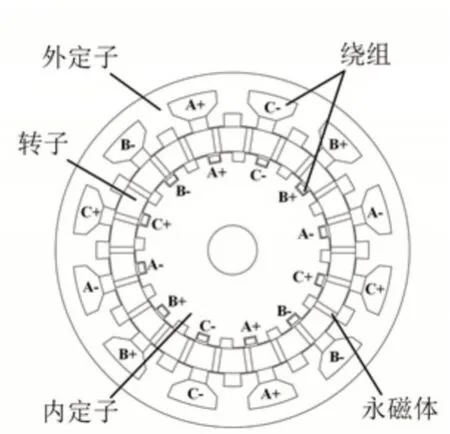
图1 新型DSPMVM的二维模型示意图Fig.1 Two Dimensional Model of DSPMVM

3 热源理论计算

3.1 DSPMVM电机的绕组铜损

DSPMVM电机适用于低速大转矩的应用场合，在工况中电枢电流的频率不高，因此可以忽略绕组线中的趋肤效应，假设DSPMVM电机的绕组线圈内电流分布均匀。

所研究的DSPMVM电机绕组为星型联接，绕组的导通方式是三相六状态两两导通，因此电机的铜损计算模型如式（1）所示：

式中：Pcu-电机的铜损；I-电机绕组的平均相电流；R-电机的单相绕组电阻。

电机在运行状态下，其相电流的有效值满足下式：

式中：I-电机运行一个周期时相电流的有效值；T-电机运行的周期。

考虑到电机在实际工作中，铜线电阻率会随自身温升的变化而发生改变，因此在对铜损的计算过程中，需要在等效热路仿真模型中增加了闭环反馈模型，引入函数f（u）。具体模型如图2所示，绕组随温升的变化关系式如下式所示：

式中：R-温升为θ时电机绕组的阻值；θa-环境温度值，规定工作环境温度为22℃；Ra-温度为θa时电机绕组的电阻值；αa-温度为θa时绕组的电阻温度系数，通常铜导线为0.00426℃-1。

3.2 DSPMVM电机的铁损

铁损是DSPMVM电机主要的热源损耗来源之一。永磁电机铁损的一般求解模型为：

式中：Pcoreloss-铁心损耗；Bm-磁通分量的幅值；f-电机频率；Kh-磁滞损耗系数；Kc-涡流损耗系数；Ke-过量铁心损耗系数。额定转速下各部分的铁损曲线，如图3所示。各部分铁心在目标电机不同转速下的铁损，如表2所示。各部分铁心在目标电机施加不同负载下的铁损，如表3所示。

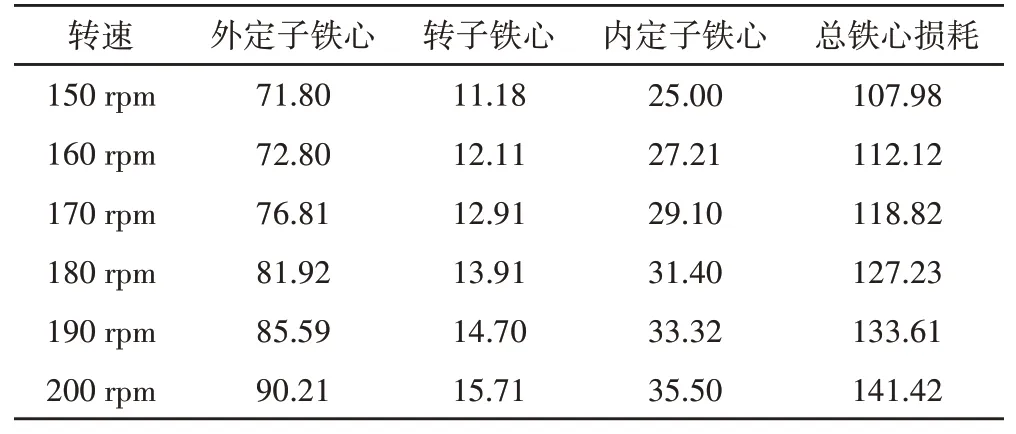
表2 电机各部分随转速变化的铁损结果（W）Tab.2 Iron Loss of Variable Parts of Motor with Speed

表3 电机各部分随负载变化的铁损结果（W）Tab.3 Iron Loss of Variable Parts of Motor with Load

图3 电机各部分铁心损耗曲线Fig.3 Core Loss Curves of Three Parts

3.3 永磁体的涡流损耗

当转子旋转时，永磁体将在交变的磁场中产生法拉第电磁感应效应，在导体中产生涡流损耗，涡流密度计算式可以表示为：

式中：Je-涡流损耗的密度；σ-永磁体材料的电导率；U-研究单元的节点间的电压；L-研究单元节点间的距离。为单独考虑目标电机内永磁体涡流损耗影响，需将目标电机工况设置为空载，并将除永磁体以外其他结构的电导率设置为零，避免其他结构产生的涡流损耗对结果产生影响。最终稳态下涡流损耗平均值，如表4所示。

表4 永磁体涡流损耗稳定值Tab.4 Eddy Current Loss of Permanent Magnets

根据表4损耗数据显示，永磁体的涡流损耗数值随着转子转速的增大呈现上升趋势，涡流损耗曲线波动也随之越大。但综合考虑，由于研究对象DSPMVM电机一般适应较低速运转状态，所以永磁体涡流损耗的数值相对较小。将其与上文已计算出的总铁心损耗数值比较分析，显然永磁体涡流损耗占比微小。所搭建的五热源等效热路模型中，忽略考虑目标电机永磁体内所产生的涡流损耗，可合理的使等效热路模型得到一定程度地简化。

4 温升仿真与比较

4.1 等效热路法

结合所提出的新型DSPMVM电机的结构特征，综合考虑DSPMVM电机内部发热、导热和散热特性，明确上述等效热路模型中等效热源以及各个部分等效热阻和等效热容，搭建DSPMVM电机五热源等效热路图，如图4所示。

图4 DSPMVM五热源等效热路图Fig.4 Five-Heat-Source Equivalent Thermal Circuit Diagram of DSPMVM

图中：PCu1-外定子电枢绕组铜损；PCu2-内定子电枢绕组铜损；PFe1-外定子铁芯损耗；PFe2-转子铁芯损耗；PFe3-内定子铁芯损耗；C1-外定子电枢绕组热容；C2-外定子铁心热容；C3-转子铁心热容；C4-内定子铁心热容；C5-内定子电枢绕组热容；V1-外定子电枢绕组热导；V2-外定子铁心热导；V3-转子铁心热导；V4-内定子铁心热导；V5-内定子电枢绕组热导；V12-外定子铁心和电枢绕组间的热导；V23-外定子铁心和转子铁心间的热导；V34-内定子铁心和转子铁心间的热导；V45-内定子电枢绕组和铁心间的热导；T1-外定子电枢绕组温升；T2-外定子铁心温升；T3-转子铁心温升；T4-内定子铁心温升；T5-内定子电枢绕组温升。

根据图4所设计电机五热源等效热路图，结合热路克希荷夫定律，可以运用微分方程表示出等效热路模型中五个热源产生热量并传递到其他部位的过程，即电机产生温升的具体计算过程，如式（6）所示：

式中：Pi-电机各部分的热源损耗；Ci-各部分的等效热容；Vi-各部分的等效热导，即等效热阻的倒数；Ti-各部分的温升值。其中，等效热阻包括了传导热阻Rc以及对流换热热阻Rf：

式中：a-平板的厚度；A-平板的换热面积；λ-物体的导热系数；h-流体对流换热系数。

基于新型DSPMVM五热源等效热路图以及搭建的温升微分计算模型，利用MATLAB内的SIMULINK模块搭建出等效热路仿真分析模型，如图5所示。模型中需要输入导热系数、散热系数等相关物理系数。电机材料的导热系数可以查阅得知，对流换热系数可根据经验公式计算得到。

图5 五热源等效热路仿真模型Fig.5 Five-Heat-Sources Equivalent Thermal Circuit Simulation Model

根据对目标电机内铁心损耗进行有限元计算得到的结果，可以计算得到目标电机在不同转速与负载下不同部位的稳态温升数值，如表5、表6所示。从表5、6中可以发现，在电机稳态温度场内，外定子绕组处于温升最大区域。这是因为外定子上端部绕组较长，铜损大且较为集中，温升最为明显。而外定子铁心因为与外定子绕组接触，且自身铁心损耗也较大，所以温升较高。总体来说，随着目标电机转速或负载的提升，其各部位温升也在增大。

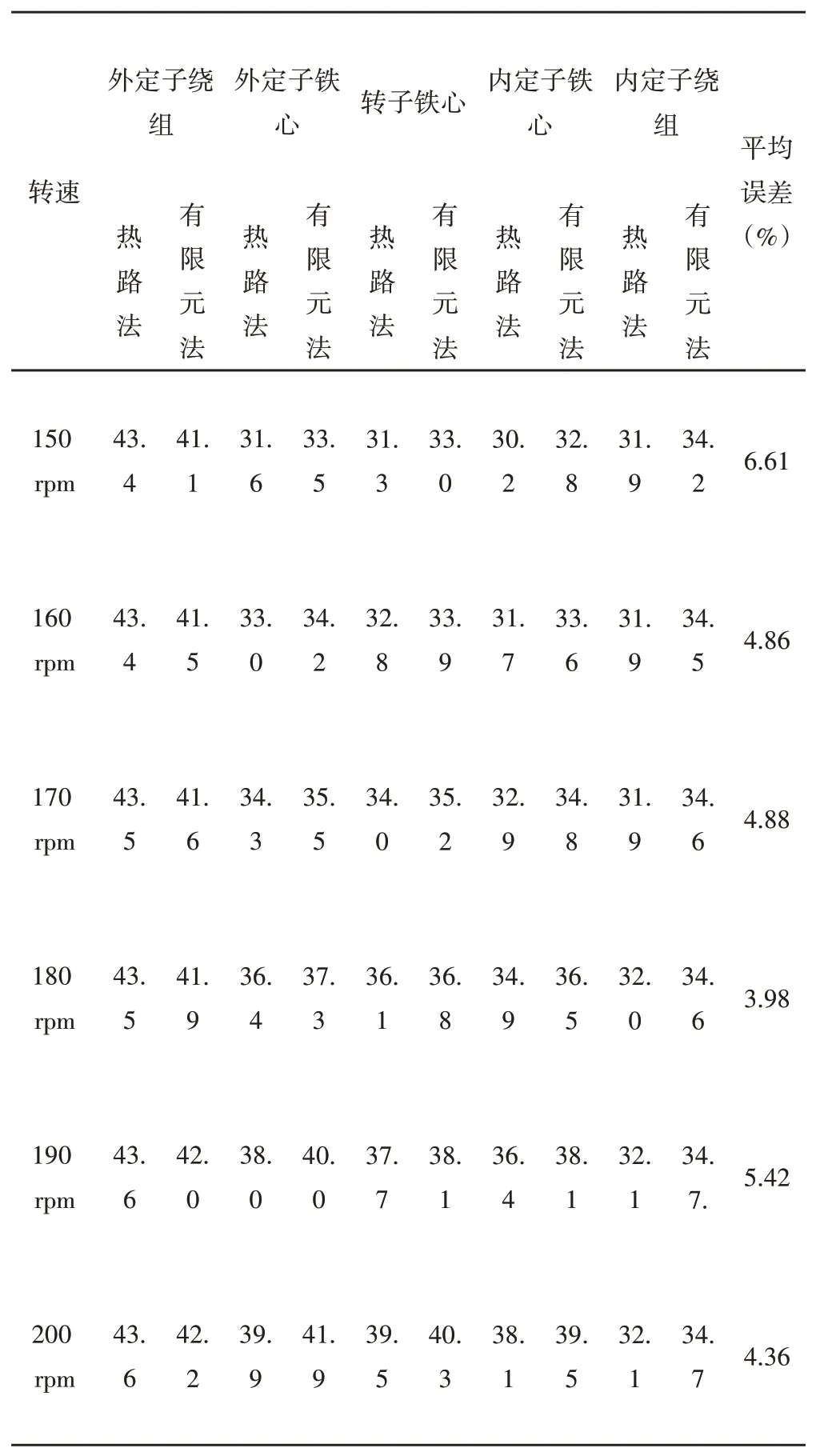
表5 不同转速下两种方法计算温升结果比较（℃）Tab.5 Comparison of Two Methods for Calculating Temperature Rise at Different Speeds

表6 不同负载下两种方法计算温升结果比较（℃）Tab.6 Comparisons of Two Methods for Calculating Temperature Rise under Different Loads

4.2 有限元仿真

利用有限元软件对DSPMVM电机稳态温度场进行仿真计算，并与等效热路法计算得到的结果进行对比。经过有限元软件磁热耦合仿真运算，得到目标电机额定转速下整体温度场分布以及截面温度场分布，如图6所示。由于电枢绕组上损耗主要是由焦耳热效应导致，其单位体积上的热量较大，因此绕组上的温升数值比铁心上的温升数值略高。

图6 额定转速下温度场（℃）Fig.6 Temperature Field at Rated Speed

4.3 对比分析

运用等效热路模型仿真计算目标电机在不同转速和负载下的温升分布结果，对比有限元温度场仿真结果，整理后如表5和表6所示。综合两种方法计算得到的结果，比较分析可知，等效热路法和有限元法二者计算的温升趋势吻合较好。温升结果的平均误差稳定在（3～7）%之间。充分证明运用两种方法对电机进行温升预测具备一定可靠性和有效性，达到准确预测电机内温升分布的目的。

为检验目标电机在上述工况内工作时温升分布是否在允许范围内，可用电机绝缘材料温升等级来验证电机内温升允许值，如表7所示。通常情况下，电机所使用的绝缘材料等级为B或E级。对比以上所求目标电机的温升结果，可以发现目标电机温升显然在绝缘允许温升范围内，证明新型DSPMVM结构设计的合理性和可行性，同时也说明该电机的热性能可得到进一步优化。

表7 绝缘温升等级Tab.7 Temperature Rise Grade of Insulation

5 结论

首先，对新型DSPMVM电机内部所产生的各种损耗进行了系统的介绍，包括不同损耗产生的机理及其计算模型，并运用有限元软件和MATLAB对目标电机在不同工况下的各损耗进行了仿真计算和分析。其次，根据目标电机的结构特点，结合电路和传热学的相关理论，提出并设计了一种五热源等效热路模型，详细阐述了该等效热路的基本原理以及数学模型，在MATLAB中完成等效热路模型地搭建。最后，运用有限元软件对目标电机进行温度场仿真，计算得到不同转速与负载工况下的稳态温度场。通过对比两种方法计算得到的结果，验证了五热源等效热路模型以及有限元3D模型的合理性和有效性，达到准确预测DSPMVM电机温升的目的，也证明DSPMVM电机结构设计的合理性。