死亡率风险对寿险公司估值的影响探究
2021-10-20南开大学金融学院
邢 辰 南开大学金融学院

一、引言
随着经济发展水平和卫生医疗水平的不断提高,我国人口的总体平均预期寿命也有逐年提高的趋势。根据国家卫健委发布的《2019年我国卫生健康事业发展统计公报》,我国的人口平均预期寿命已经从2018年的77.0岁提高到2019年的77.3岁。各年龄死亡率不断下降的趋势无疑会导致保险产品价值的波动,从而影响保险公司估值的准确性,最终影响经营决策。
目前国内外的相关研究主要关注死亡率风险的衡量和管理手段。学术界对死亡率风险管理手段的研究主要分为两种:
第一种是自然对冲手段,即利用死亡率变化对寿险和年金产品影响方向相反的特点,合理配置两种产品以规避风险。Jeffrey(2009)用CBD 模型拟合死亡率,设定目标函数为使损失波动的条件风险价值(CVaR)最小,并加入了利润约束的条件,来决定销售产品的最优化配比。Jennifer(2010)使用Lee-Carter模型来拟合死亡率,并采用死亡免疫的方法计算最佳寿险—年金产品组合比例,以规避寿险公司面临的长寿风险。Wang(2013)假设保险公司的资产组合由无风险债券、寿险保单和年金保单组成,资产组合的价值变化同时受利率风险和死亡率风险的影响,得出了可以最小化其变化幅度的最优产品组合。在国内相关研究中,李冰清(2016)应用CBD模型刻画随机死亡率,并在偿付能力的约束下探究保险公司在不同产品线上的最优资本配置。
第二种是风险管理手段,即利用死亡率相关衍生品,如长寿债券、长寿互换等,来实现死亡率风险的管理。Wong(2017)采用双随机复合泊松过程对保险负债建模,研究了保险公司使用长寿债券或长寿互换的动态均值差异对冲问题,并推导出了最优对冲策略。国内的相关研究中,艾蔚(2011)探讨了利用死亡率相关的衍生工具管理死亡率风险的可行性,并对比分析了不同衍生品的风险管理有效性。
除了死亡率风险的衡量和管理,国内外在死亡率风险的影响方面的研究分析也取得了一定进展。Jeffrey 等(2000)分析探讨了死亡率风险对寿险公司年金产品的趸交保费可能产生的影响,研究认为寿险公司在为年金产品厘定费率时需要充分考虑未来死亡率可能存在的改善趋势。Gründl(2006)以股东价值(SHV)最大化为目标,分析了死亡率风险对保险公司的最佳风险管理组合(权益资本、资产配置和产品政策)的影响。Gatzert(2012)采用自然对冲的风险管理方法,量化了死亡率变化对寿险公司违约风险的影响。文章认为,为了更深入地了解自然对冲对保险公司风险状况的影响,同时考虑资产和负债两方面是非常重要的。Nadine(2014)分析了自然对冲、死亡率衍生品两种风险管理手段对不同类型死亡率风险的有效性。Anton.S(2019)从股东和被保险人两个角度,研究了德国寿险公司资产组合中应用自然对冲策略对权益头寸产生的影响。国内的相关研究主要集中在死亡率风险对产品的保费厘定及准备金产生的影响。祝伟(2012)研究发现,未来死亡率的改善会明显提高个人年金业务的支付现值,从而对定价和准备金管理产生影响。谢漫锜等(2013)拟合了不同性别各年龄死亡率的改善情况,并分别探究了死亡率改善对于寿险和年金产品责任准备金变动情况的影响。孙佳美(2014)利用Monte Carlo 方法模拟了未来死亡率,并在模拟死亡率和静态死亡率假设下分别探究责任准备金风险的变化情况,研究发现,死亡率的改善会明显改变产品准备金的分布及波动情况。
然而,现有关于死亡率风险影响的研究大多数局限于产品层面或单纯的公司风险管理层面,没有考虑到公司估值的因素。而在实务中,无论是从公司内部、股东还是监管角度出发,寿险公司估值的准确性都非常重要。如果死亡率风险影响了公司实际估值,公司内部可能会做出错误的长期经营决策;股东方面有可能会被偏差的公司估值误导而蒙受损失;估值不准确也可能导致监管机构错误评级,影响公司长期发展。
鉴于此,本文将死亡率风险和公司估值两个方面的因素同时纳入考量,为寿险公司风险管理提供新的视角。研究将基于两个方面:一是对未来不同年龄人口死亡率的合理建模、拟合和预测;二是在固定死亡率和预测死亡率假设下研究公司估值的分布情况。为了简化分析,本文假设死亡率风险是寿险公司的全部风险来源,也就是说,在本文框架下我们不再考虑信用风险、市场风险等其他风险因素。本文采用CBD模型拟合不同年龄人口的死亡率数据并在此基础上进行预测,探究在不同死亡率假设的框架下,寿险公司价值的波动情况。本文的创新之处在于,将死亡率风险和公司估值因素联系到一起,为寿险公司的估值和风险管理提供了全新视角。
二、模型设计
(一)未来死亡率拟合模型:CBD模型
CBD 模型包含了两个时间效应参数,可以用于对随机死亡率进行拟合和预测,最早由Cairns等(2006)提出。CBD模型的基本表达式结构如下:
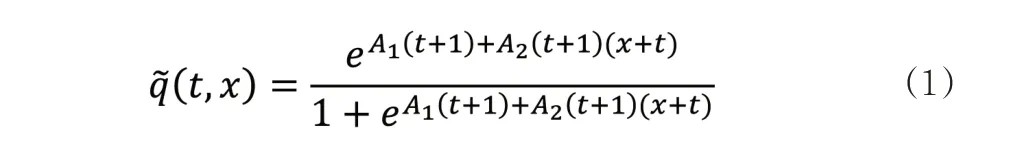
其中,t为离散时间;x是年龄;为x岁的人在t到t+1期间死亡的概率。模型里的两个因子A1(t)和A2(t)代表了所有年龄面临的死亡率随时间推移的改善情况,其中A1(t)随时间推移逐渐下降,其作用是以相同程度改善所有年龄的死亡率;而A2(t)为正值,其作用是使得死亡率随时间的改善程度因年龄段的不同而有所差别,其中低龄人群的死亡率随时间的改善更为明显。这两个因子同时代表了死亡率随时间变化的改善趋势效应和年龄差异效应。当我们考虑因子随时间的参数变化时,CBD模型将具有经济或生物学意义。
进一步地,为了预测A(t)=(A1(t),A2(t))'的未来分布情况,CBD模型把A(t)假设为带有漂移项的二维随机游走:
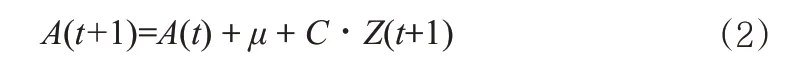
其中,μ为2×1的常量矩阵;C为一个2×2的上三角矩阵,从半正定矩阵V=C∙C'分解而来;Z是二维标准正态随机变量。
Cairns 等(2006)令D(t)=A(t)-A(t-1),并通过非信息性的先验分布,证明了μ,V满足normal-inverse-Wishart分布。
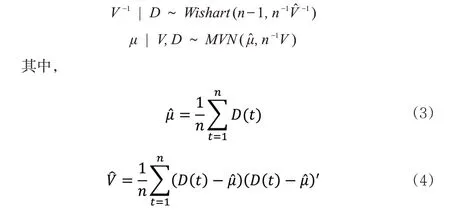
根据以上信息,本文即可对未来死亡率进行拟合和预测,并进一步对公司估值情况进行探究。
(二)公司估值模型:内含价值法
寿险公司的产品往往期限较长,而当期利润主要来自之前保单的剩余边际释放,因此无法简单地用当期会计利润来衡量公司运营状况或评估公司价值。鉴于此,本文将使用行业内常用的内含价值法来作为公司估值模型。
内含价值法(Embedded Value)的相关概念最早由Anderson 提出。他认为,由于寿险行业资产和负债存在特殊性,寿险公司的真正价值不能用一般企业的估值方法来合理反映,而是应该综合考虑全部有效保单以及新业务保单在未来可能创造的价值。Bangert(1973)在Anderson(1959)思想的基础上详细解释了“有效业务价值”和“新业务价值”的定义并给出两者的计算方法,同时他也认为,可以利用未来现金流折现加总的思想来衡量寿险公司的真实价值。随着相关理论不断发展,欧洲部分国家开始要求寿险公司在其年报内必须报告其内含价值。国内的相关应用起源于2005 年原保监会发布的《人身保险内含价值报告编制指引》,文件中首次提出了寿险公司进行内含价值评估的强制要求。随着中国偿二代框架不断完善,2016 年中国精算师协会发布《精算实践标准:人身保险内含价值评估标准》,进一步要求我国寿险公司应当充分具备准确评估内含价值的能力。
内含价值模型的基本思想是,寿险公司真实价值应该等同于公司现有净资产的总价值与未来预期会实现的收益现值的和。其简要表达式如下:
评估价值(AV,Appraisal Value)=内含价值(EV)+新业务价值(VNB,Value of New Business)
其中,内含价值被定义为公司持有资产的市场价值+公司保单的有效业务价值-公司持有要求资本的成本,这里的有效业务价值是指公司当前有效保单预计可以产生的、最终将归属于股东所有的现金流的现值;新业务价值则被定义为评估日前一年签发的所有保单未来预计产生的股东现金流的现值。
本文的后续部分将假设公司原本没有任何有效保单,所有保单将在初始时刻作为新保单同时售出,故在本文研究框架下不存在有效业务价值。为简化研究,本文将使用新业务价值指标代表公司估值。
在评估时点T,公司的新业务价值等于未来各期预计可分配盈余现值扣除评估时点的要求资本。其表达式如下:
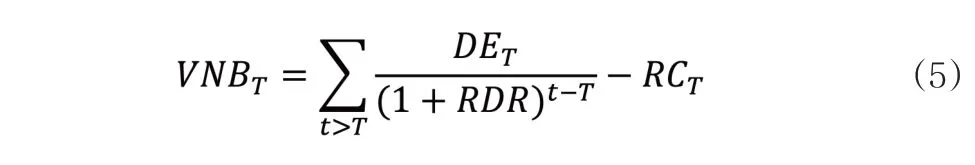
1.要求资本RC(Required Capital),是为了满足监管机构对保险公司提出的偿付能力要求而必须留存的资本量。在内含价值模型框架下,RC可以表示为:
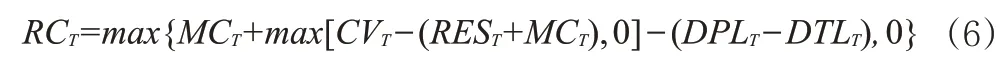
其中,MC(Minimum Capital)为监管机构要求公司持有的最低资本(Minimum Capital),由各子风险的预测资本载体乘以对应的最低资本预测因子,并通过一定方式汇总得出;CV(Cash Value)为保单的现金价值;RES为保单的准备金(Reserve);DPL为保单的剩余边际(Deferred Profit Liability),来源于首日利得的摊销,可以用摊销载体和摊销因子相乘得出;DTL为剩余边际对应的应交税金。因DTL=DPL×税率,故DPL-DTL为税后剩余边际。
2.未来可分配盈余DE(Distributable Earnings),等于公司业务的税后净利润和可投资净资产所得收益的总和。DE可以被表示为:
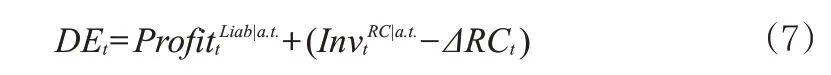
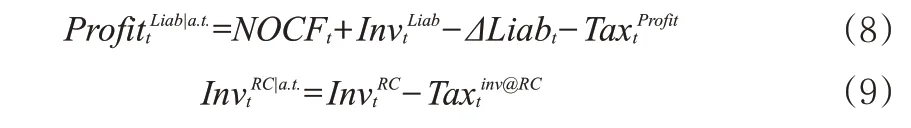
式(8)中,NOCFt为净经营现金流的最优估计,为准备金投资收益,ΔLiabt为寿险业务负债提转差(Liabt-ΔLiabt-1),为所得税支出。式(9)中,可投资净资产的税后投资收益则由要求资本的投资收益扣减相关税费()计算得出。需要注意的是,在偿二代假设框架下,寿险业务负债应该等于法定准备金(RES)与剩余边际(DPL)的和。
根据上述信息,把未来各期可分配盈余的表达式整理如下:
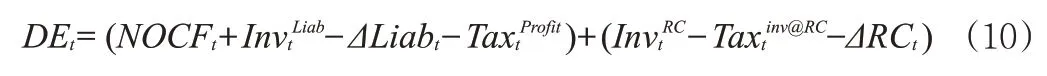
3.风险贴现率RDR(Risk-adjusted Discount Rate),被定义为将风险因素纳入考量范围后经调整得出的贴现率,用于计算未来可分配盈余的折现值。
由此,通过式(5)(6)(10),我们便可以计算出公司的新业务价值,并以其作为本文中寿险公司价值的合理预估。
三、参数假设及研究步骤
(一)数据来源及处理
本文使用我国1994—2019 年共计26 年的30 岁及以上男性经验死亡率的相关数据,并合理使用CBD 模型进行拟合。数据来源于1995—2006年《中国人口统计年鉴》、2007—2020年《中国人口与就业统计年鉴》,以及《中国2000年人口普查资料》和《中国2010年人口普查资料》。
原始数据中多数年份的年龄组别为30~89岁各年龄和90岁及以上,因此本文采取同样的年龄分组方式,并对少数年份的数据进行调整。其中,1995年、2000年、2005年、2010年、2015年死亡率数据的年龄组别为30~99岁各年龄和100岁及以上,本文将这些年份中90岁及以上各年龄的平均人口数和死亡人口数分别加总并手工计算得出90岁以上年龄段的死亡率;1996年死亡率数据的年龄组别为30~84岁各年龄和85岁及以上,本文采取邻年线性插值的方法计算此年85~89岁各年龄和90岁及以上组别的死亡率。
(二)产品组合及相关参数设定
1.寿险公司产品组合设置
本文将产品组合设定为寿险公司主要出售的两种典型产品:寿险和年金,全面考察死亡率的未来变动对公司估值可能造成的影响。由于死亡率相关数据的年龄最高组别为90 岁及以上,无法保证该组别各年龄模拟未来死亡率的准确性,因此本文将目标险种设置为定期寿险和递延定期年金,具体设定如表1所示。
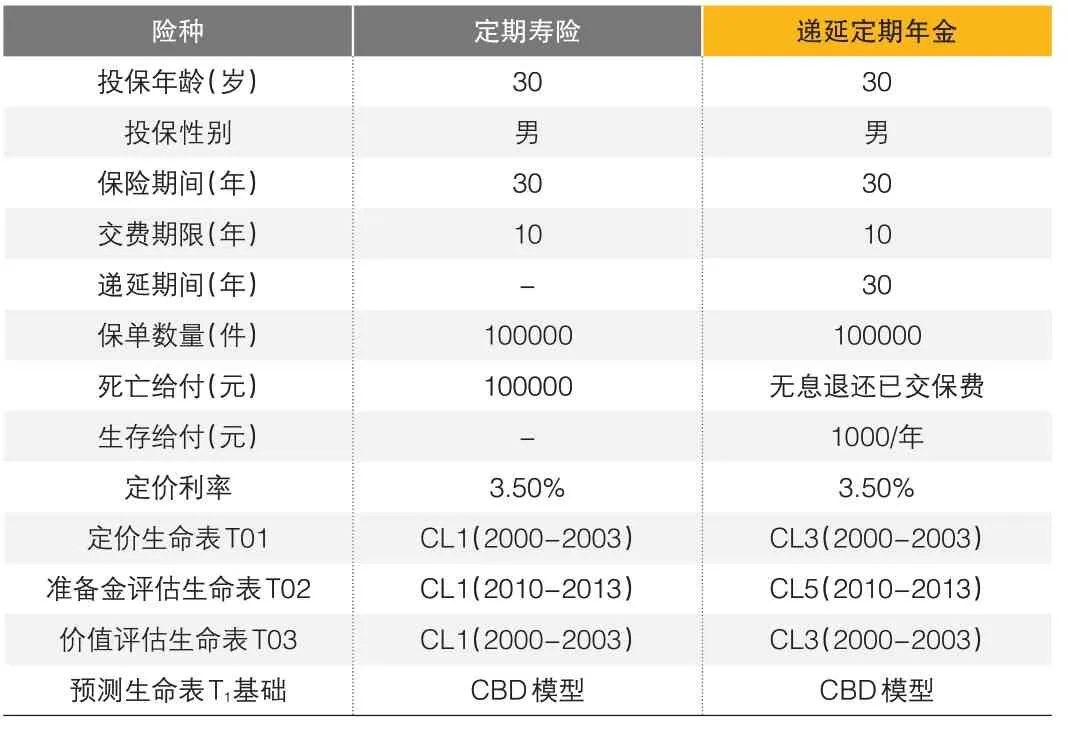
▶表1 寿险公司产品组合设置及其相关参数
2.公司价值评估有关假设及其参数设置
本文将在偿二代假设下进行公司价值评估过程。需要注意的是,由于本文重点在于考察死亡率风险对公司价值评估的影响,因此在计算各期要求资本时将只在模型中纳入死亡风险,而忽略信用风险等偿二代框架中包括的其他风险。根据偿二代下寿险公司新业务价值评估的一般原则和经验假设,本文设置了相关参数,如表2所示。

▶表2 公司价值评估相关参数设置
(三)研究步骤
产品定价过程中如果没有充分考虑到未来死亡率的改善趋势,保费可能会被高估或低估,从而影响公司估值的准确性。鉴于此,本文首先根据行业内普遍使用的生命表对两种产品进行定价和估值,再模拟不同死亡率假设下公司估值的波动情况。具体研究步骤如下:
1.对两种产品分别建模,在给定生命表T01和T02的假设下对其定价和评估准备金。
2.在价值评估阶段,首先设置初始保单数量,并假设死亡人数是关于给定生命表T03 的二项分布,模拟出各年龄的死亡人数,结合步骤1 中的保单价格及准备金,得出在此情境下的产品价值;将此步骤重复10000 次,即可得出给定生命表T03 假设下的公司估值波动情况。
3.以CBD 模型为基础,模拟出10000 张预测生命表,并取其期望值,作为预测生命表T1。
4.用预测生命表T1替换给定生命表T03,把步骤2重复10000次,即可得出预测生命表假设下的公司估值波动情况。
5.在步骤2 和步骤4 得出公司估值的两种分布情况的基础上,分别计算其期望值、标准差、偏度、峰度、VaR值和CVaR值,并通过对比两种情境,来探讨死亡率风险对寿险公司估值的准确性及波动情况可能产生的影响。
四、基本结果
(一)基于CBD模型的随机死亡率预测
本文利用CBD模型和最小二乘法,根据式(1)拟合我国1994—2019年30岁及以上男性经验死亡率数据,参数估计结果如图1所示。
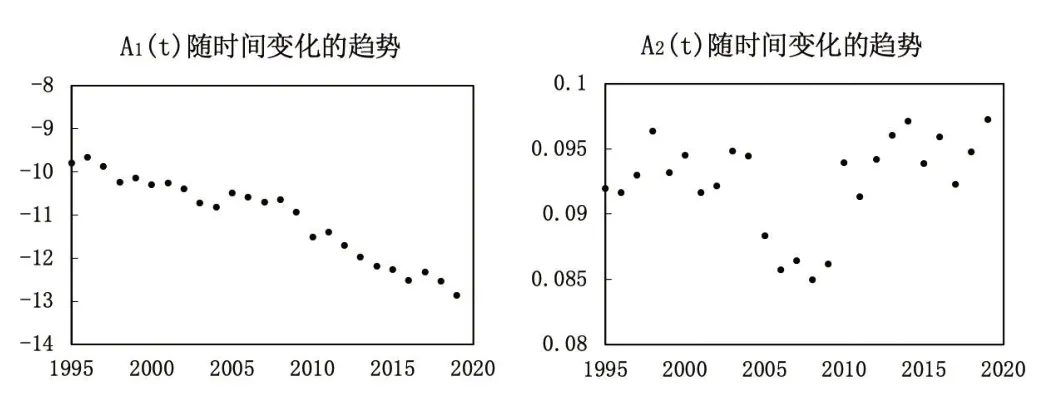
▶图1 CBD模型拟合结果
从图1可以看出,A1(t)随时间推移有逐渐下降的趋势,这表明各年龄死亡率随时间推移整体有所改善;A2(t)则存在不规则的波动趋势,且估计值都是正值,这表明随着时间推移,各年龄死亡率的改善情况并不相同,即年龄越大,其死亡率随时间的改善效果就越弱。

(二)不同死亡率假设下的公司价值评估分析
1.给定生命表下的公司价值评估分析
本文对两种产品分别建模,首先在给定生命表的假设下模拟了两种产品新业务价值和公司价值的波动情况,其分布直方图如图2和图3所示。同时,本文也计算了三者模拟分布的期望值、标准差、偏度、峰度、VaR和CVaR值,以便于后续的定量探讨,具体结果如表3所示。

▶图2 给定死亡率下两种产品新业务价值分布情况(单位:元)

▶图3 给定死亡率下公司价值分布情况(单位:元)
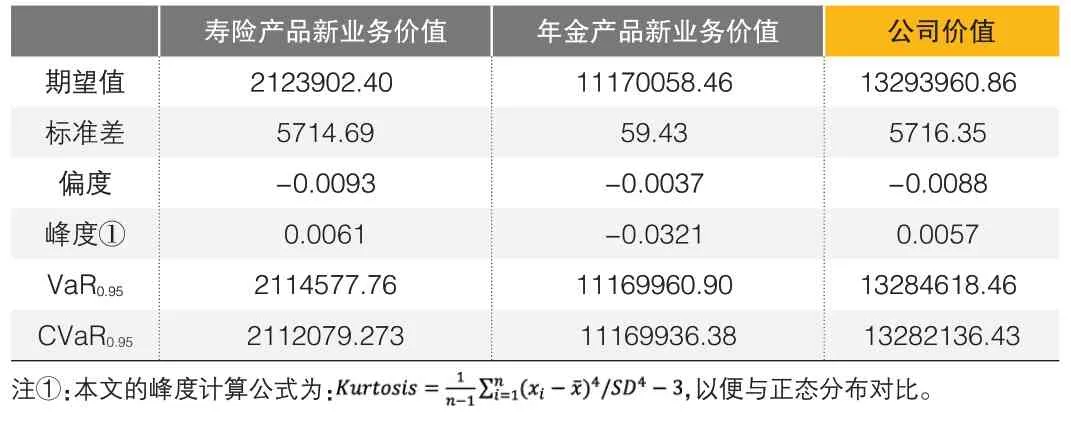
▶表3 给定生命表下的公司价值波动分析(单位:元)
从图2和图3中可以看出,虽然两个险种的保障内容不同,但当实际死亡率围绕给定死亡率波动时,两个险种的新业务价值均会受到影响,导致公司价值也出现波动,其分布接近于正态。
下面根据表3 进行具体分析。三种分布围绕期望值有不同程度的波动,各自的偏度和峰度均接近于0,即分布情况均近似于正态;VaR0.95和CVaR0.95均为正值。值得注意的是,寿险和年金产品的新业务价值标准差分别为5714.69 和59.43,即在给定假设下,死亡率波动导致的寿险产品新业务价值波动幅度明显大于年金产品。这可能是因为本文设定的年金产品同时包括生存给付和死亡给付,而两者受死亡率变动的方向相反,起到了对冲作用,因此年金产品的新业务价值相对稳定。但因受到寿险产品的影响,公司价值的波动仍较为明显。
2.预测生命表下的公司价值评估分析
为了考察死亡率的改善对公司实际价值产生的影响,我们使用CBD模型拟合并预测未来死亡率,以此建立预测生命表,并基于预测生命表及其波动,重新评估两种产品的新业务价值及对应的公司价值,其分布直方图如图4和图5所示。我们同样给出了预测生命表假设下三者模拟分布的期望值等主要统计指标,具体结果如表4所示。
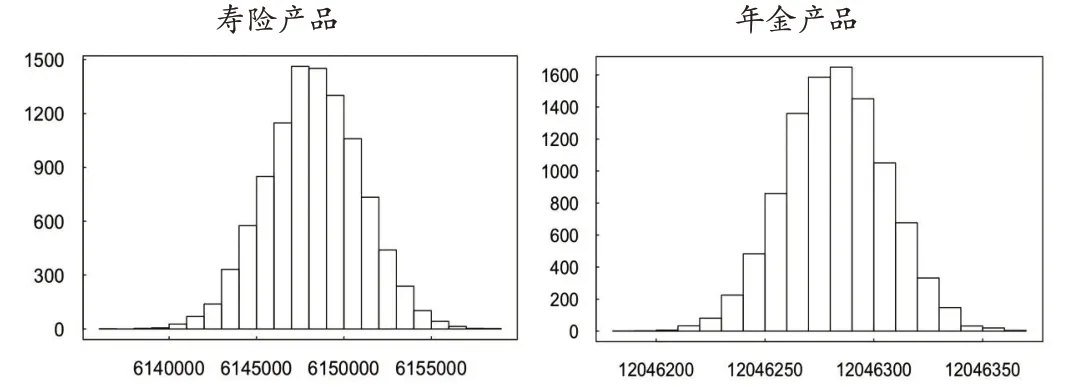
▶图4 预测死亡率下两种产品新业务价值分布情况(单位:元)
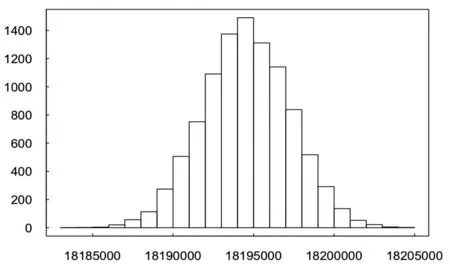
▶图5 预测死亡率下公司价值分布情况(单位:元)
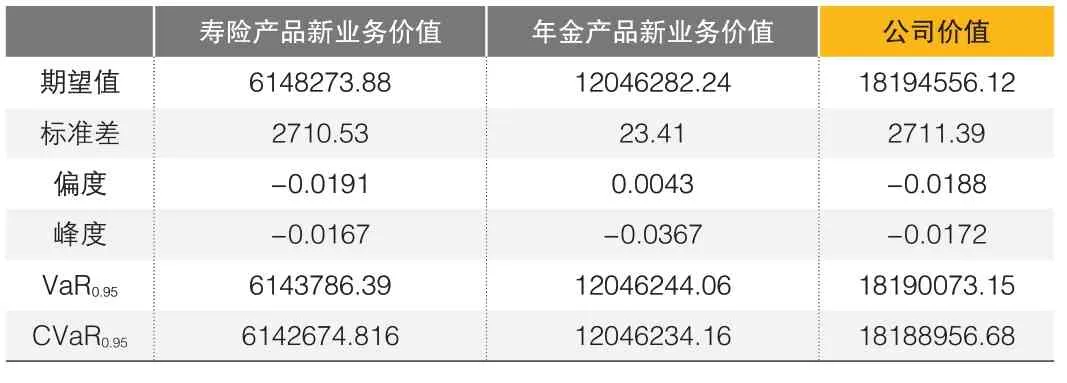
▶表4 预测生命表下的公司价值波动分析(单位:元)
从上述结果可以看出,当考虑到死亡率的改善时,两种产品新业务价值和公司价值的偏度和峰度与表3相比没有太大变化,仍然接近正态分布;但三者的期望值、VaR0.95、CVaR0.95都有不同程度的提高,这意味着在给定死亡率下,无论是两种产品新业务价值还是公司价值都被明显低估了。此外,三者模拟分布的标准差都有所降低,这意味着估值时如果充分考虑了死亡率改善,就可以使公司价值的波动幅度相对减小,有利于公司长期稳定经营。
3.不同死亡率下公司价值分布对比分析
对于寿险产品来说,死亡率的改善意味着未来死亡赔付的现值会降低,因此,如果估值时未考虑死亡率的改善,则会低估寿险产品的新业务价值。而对于年金产品来说,死亡率的改善一方面意味着预期寿命延长,生存给付的现值会提高;另一方面年金产品中死亡给付现值则会降低。因此,当年金产品中同时包括生存给付和死亡给付时,其新业务价值受到死亡率改善的影响方向并不确定,取决于两种变动方向的总效应。在本文的假设下,寿险产品的新业务价值变动非常明显,其期望值比给定死亡率下的期望值高出189%;年金产品新业务价值的变动幅度则相对较小,其期望值比给定死亡率下的期望值高出7.84%,这意味着死亡率的改善会导致两种产品的新业务价值同时被低估。两者加总后,公司价值的期望值则比给定死亡率下的预估价值高出36.86%,这意味着在本文框架下,如果寿险公司估值时没有把未来人口死亡率可能存在的改善趋势充分纳入考量,评估出的公司价值将比其真实价值降低近30%。
由此可知,未来死亡率的改善会显著影响寿险公司估值,如果不采取措施修正估值时的死亡率假设,公司估值的准确性会大大降低,最终影响到公司经营决策和长期发展。因此,寿险公司在估值时需要充分考虑未来死亡率可能存在的变动。
五、结论
本文考察了死亡率风险对寿险公司价值评估可能产生的影响,在寿险公司的估值和对应的风险管理方面给出了全新视角。本文借助CBD模型和内含价值评估方法模拟了在给定死亡率和预测死亡率下寿险公司价值的分布,从而分析未来死亡率的改善对公司价值带来的影响。本文的产品模型在偿二代框架下搭建,对寿险公司来说更具有借鉴意义。
研究结果表明:(1)无论是在现有生命表还是预测生命表的假设下,在年金产品同时包含生存给付和死亡给付时,其自身的对冲作用使得新业务价值受死亡率影响的幅度显著小于寿险产品。(2)死亡率的改善会提高寿险产品的新业务价值,但年金产品自身的对冲作用使得新业务价值受影响的方向并不确定。如果两种产品受影响的方向相反,则可以考虑通过自然对冲的方式稳定公司价值。(3)死亡率的改善会显著影响寿险公司估值,如果估值过程中没有充分考虑未来死亡率改善的因素,则可能导致公司估值和实际价值产生较大偏差,影响公司长期发展。因此,寿险公司在估值的过程中需要充分考虑到未来死亡率变动的因素。
本文首次将死亡率风险和公司估值因素联系到一起,对寿险公司估值过程中的风险管理有一定指导意义,当然也存在不足。未来的改进方向可能有以下几点:(1)本文假设死亡率风险是寿险公司面临的全部风险来源,因此未来可参考寿险公司实际估值过程,将信用风险、市场风险等偿二代下同样关注的风险因素也纳入考量范围,使文章更具有现实意义;(2)本文对寿险和年金产品使用了相同的预测生命表,未来可将逆选择效应纳入考量,对两种产品分别拟合出不同的预测生命表,以反映两种产品保单持有人不同的潜在死亡风险;(3)本文侧重于死亡率风险对公司价值产生的影响,未来可在此基础上进一步考虑自然对冲等死亡率风险管理手段,对寿险公司准确估值提供更大的参考价值。
