C- -Re 高超声速三维边界层转捩预测模型
2021-10-20向星皓张毅锋袁先旭涂国华万兵兵陈坚强
向星皓,张毅锋,袁先旭,涂国华,万兵兵,陈坚强,2,*
1.中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
2.中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
高超声速三维边界层横流转捩的准确预测是高超声速飞行器气动设计面临的主要困难之一。由于飞行器三维曲面构型和飞行姿态角(攻角、侧滑角)的影响,边界层内往往存在与无黏流线方向垂直的流动分量,称为横流流动[1]。在真实飞行中,由横流速度拐点导致的横流失稳机制在三维边界层中普遍存在,并成为三维边界层转捩的主导因素[2]。
基于雷诺平均Navier-Stokes(RANS)方程的转捩模型是解决转捩实际工程问题的重要手段。在高超声速横流转捩模型方面,王亮[3]提出了k-ω-γ新型湍流/转捩模型,对高超声速圆锥预测效果良好;周玲等[4]基于传统横流雷诺数判据对k-ω-γ转捩模型进行了改进;张毅锋等[5]改进的γ-Reθ t转捩模型实现了对零攻角尖锥、椭锥表面转捩阵面模拟;徐晶磊等[6]提出了KDO(Kinetic Dependent Only)单方程湍流/转捩一体化模型,实现了对椭球体、尖锥表面的转捩预测。此外,国内外进行了大量的低速横流转捩模型与判据研究[2,7],取得了较好的预测效果,但在高超横流转捩方面的模型研究较少。
目前高超声速横流转捩领域由于缺乏足够丰富的变参数试验结果,例如表面粗糙度、噪声等,高超声速横流转捩判据与预测模型的构建与应用遇到较大困难。本文采用线性稳定性分析eN方法对高超声速横流转捩数据进行拓展,结合横流强度与表面粗糙度构造当地化的高超声速横流转捩判据,面向高超声速三维边界层对基于Chant 2.0计算平台的高超声速修正γ-Reθ转捩模型进行完全当地化的横流拓展,建立适用于高超声速三维边界层转捩预测的C-γ-Reθ横流转捩预测模型。
1 计算方法
1.1 控制方程
采用有限体积法求解RANS方程。无黏通量采用AUSM(Advection Upstream Splitting Method)格式、二阶精度MUSCL(Monotonic Upwind Scheme for Conservation Law)格式离散,利用Van-Leer和Minmod混合限制器捕捉激波间断。黏性通量采用二阶中心差分格式离散,时间推进采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式方法,采用MPI(Message Passing Interface)技术进行并行计算。
1.2 基础转捩模型
湍流模型采用两方程k-ωSST(Shear Stress Transfer)模型。基础转捩模型采用基于Chant 2.0高超计算平台的高超声速修正γ-Reθ转捩模型[5],能够预测无攻角情况下的高超声速平板、直锥、裙锥等的流向转捩。

(1)
(2)
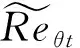
(3)
(4)
(5)


(6)
(7)
式中:Mae为边界层外缘马赫数;C1~C4为修正系数[5];y为壁面距离;v为黏性系数。
高超声速修正包括压力梯度参数修正与湍流普朗特数修正[5],使之能够预测无攻角情况下的高超声速尖锥流向转捩,如图1[5]所示,图中x为轴向位置,对比了无修正、压力梯度参数λθ修正以及两种(λθ+Prt)修正叠加γ-Reθ模型预测的尖锥壁面温度回复因子r分布。

图1 尖锥壁面温度恢复因子r分布[5]Fig.1 Temperature recovery factor r distribution on sharp cone surface[5]
2 构建横流转捩模型
能体现流动物理机制的高保真模型是提高CFD计算结果精准度的重要基础[7]。从现有模型和判据的构造出发,说明γ-Reθ转捩模型无法预测横流转捩的原因,并阐释基于传统横流雷诺数判据的横流模型在高超声速横流转捩预测中失效的机制。在此基础上通过线性稳定性eN方法对高超声速横流转捩数据进行拓展,利用横流强度与壁面粗糙度构造当地化的高超声速横流转捩判据,对γ-Reθ转捩模型进行高超横流拓展,初步建立适用于高超声速三维边界层的C-γ-Reθ转捩预测模型。
2.1 γ-Reθ转捩模型的横流预测不适用性

动量厚度雷诺数输运方程的生成项定义为
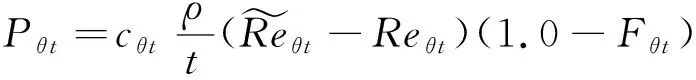
(8)
式中:cθ t为生成项系数,cθ t=0.03;Reθ t为经验关系拟合雷诺数;Fθ t为边界层识别函数,使源项在边界层外开启,在边界层内关闭。因此在边界层外,输运量趋于当地拟合值Reθ t;在边界层内,输运量主要依靠扩散作用。该边界层识别函数也被用于横流源项构造。
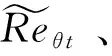

图2 椭球表面摩擦力系数分布[10]Fig.2 Skin friction coefficient distributions on prolate spheroid[10]
2.2 低速横流判据/模型的高超声速不适用性
传统横流雷诺数判据一般将横流雷诺数定义为Recrossflow=Wmaxδ10%/v,其中Wmax为沿壁面法向的最大横流速度,δ10%为横流速度为最大横流速度10%的位置(壁面较远处)对应的壁面法向距离。
天津大学赵磊[9]发现,同一流场中采用边界层名义厚度δ99无量纲化的横流速度型几乎完全重合,如图3[9]所示,其中us和uc分别为按其最大值归一化的势流方向速度和横流方向速度。这意味着不同站位下的δ10%/δ99基本上是一定的,令其比值等于Cδ,则有
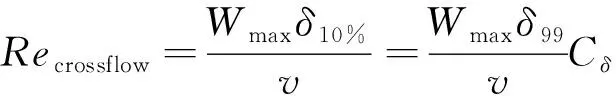
(9)
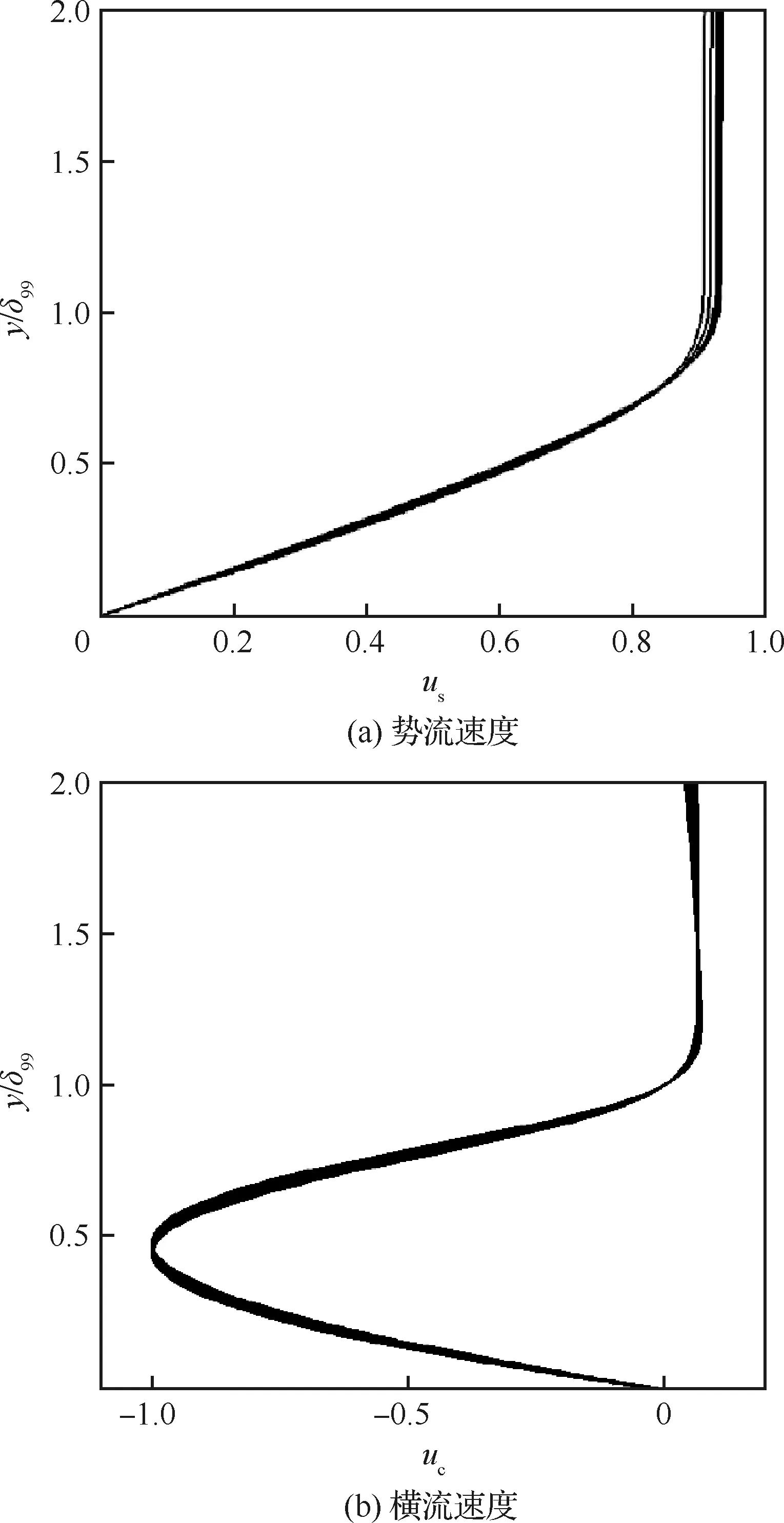
图3 超声速后掠钝头平板不同站位归一化势流、横流速度分布[9]Fig.3 Normalized potential flow and crossflow profiles at different locations for hypersonic swept blunt plate[9]
式中:δ99和v与来流相关。
通过超声速、高超声速尖锥数值计算发现,最大横流速度Wmax与来流马赫数紧密相关,并且变化幅度较大。图4为固定雷诺数、来流马赫数Ma=3~7情况下,尖锥侧面90°子午线最大横流速度沿轴向的分布。对于横流速度的马赫数相关性,赵磊在钝头后掠平板流动中也有类似发现[9]。由图4可知,尖锥表面横流强度大部分情况下超过12%,该强度也超过了Reed和Haynes[11]提出的横流准则适用范围,即最大横流速度Ucf,max与边界层外缘速度Ue比值不超过8%(Ucf,max/Ue≤8%)。固定来流雷诺数前提下,最大横流速度具有较强的马赫数相关性,导致采用单一临界值的横流雷诺数判据在图4所示高超声速情况下不再适用。

图4 不同马赫数下尖锥表面90°子午线最大横流速度分布Fig.4 Max crossflow velocity distribution for 90° meridian line on sharp cone surface with different Mach numbers
Langtry[12]基于当地涡强度和表面粗糙度提出了当地化低速横流转捩拓展方案,针对γ-Reθ模型进行了横流拓展。其横流转捩判据实现了当地化,脱离了传统横流雷诺数的定义形式,判据主要应用于低速流动。图5为在Chant 2.0平台实现的Langtry低速横流转捩模型对于亚声速条件下NFL(2)-0415后掠翼于不同来流雷诺数下的风洞状态,图中Rec为弦长雷诺数,(x/c)tr为以弦长c进行无量纲化的转捩位置,模型预测的横流转捩位置与实验结果[13]较为符合,模型性能显著优于γ-Reθ原始模型。
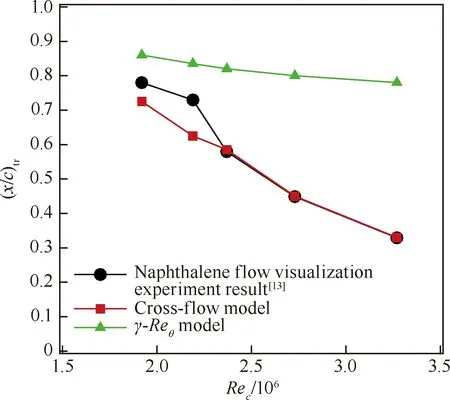
图5 后掠翼表面横流转捩预测Fig.5 Crossflow transition prediction on swept wing surface
经测试,Langtry横流转捩模型在高超声速横流转捩预测中会出现转捩位置滞后或者不发生横流转捩的情况。如图6所示,低速横流模型预测的尖锥迎风面转捩阵面相比风洞试验[14]显著延后,在试验窗口内未能观测到转捩现象。转捩模型和风洞试验的转捩位置见表1。
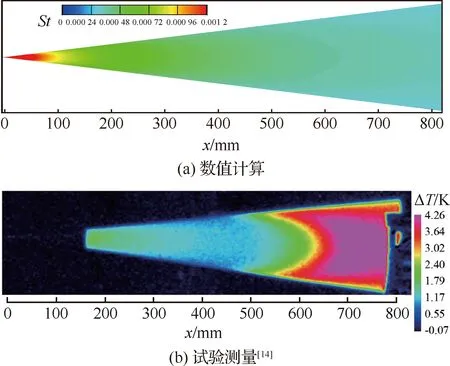
图6 攻角α=2°时迎风面低速横流模型计算斯坦顿数St分布与风洞试验[14]温升ΔT分布Fig.6 Stanton number St distribution of low-speed cross-flow model calculation and temperature rise ΔT distribution of wind tunnel experiment[14] at windward side when angle of attack α=2°

表1 转捩位置Table 1 Transition location
2.3 构建高超声速横流转捩判据
参照Langtry低速横流转捩判据的构建形式,以稳定性拓展的直接数值模拟数据[15]为基础构造了适用于高超声速横流转捩的预测判据。
现有横流雷诺数转捩判据不适用于高超声速横流转捩,而高超声速横流转捩判据的构建受限于试验数据的缺乏,尝试采用线性稳定性eN方法的拓展技术[16]对变表面粗糙度的高超声速椭锥横流转捩DNS(Direct Numerical Simulation)数据[15]进行拓展。表面粗糙度是指由于表面加工导致的分布式粗糙度,粗糙高度单位为μm,在实际风洞试验中由触针法测量。根据“临界横流雷诺数ReCF,crit-表面粗糙高度h”数据组构造考虑表面粗糙度的横流转捩判据,并对判据进行当地化处理。拓展后的“ReCF,crit-h”数据一共分为9组,每组3个数据点,共计27个数据点,如图7[17]所示。考虑攻角和表面粗糙度,研究多重因素影响下的转捩临界横流雷诺数ReCF的变化规律。
高超声速椭锥在α=0°, 1°, 2°下的高超声速(Ma=6)横流转捩临界雷诺数呈现出明显的规律性,如图7所示。判据规律具体表现为:① 在相同来流状态与飞行姿态下,对数坐标下的椭锥表面临界横流雷诺数ReCF,crit与表面粗糙度呈现出较强的线性相关性;② 有攻角条件下该线性拟合关系的斜率与截距几乎不受来流雷诺数的影响;③ 随攻角变化,椭锥表面的横流强度发生变化,“ReCF-h”线性关系沿纵轴整体发生平移。
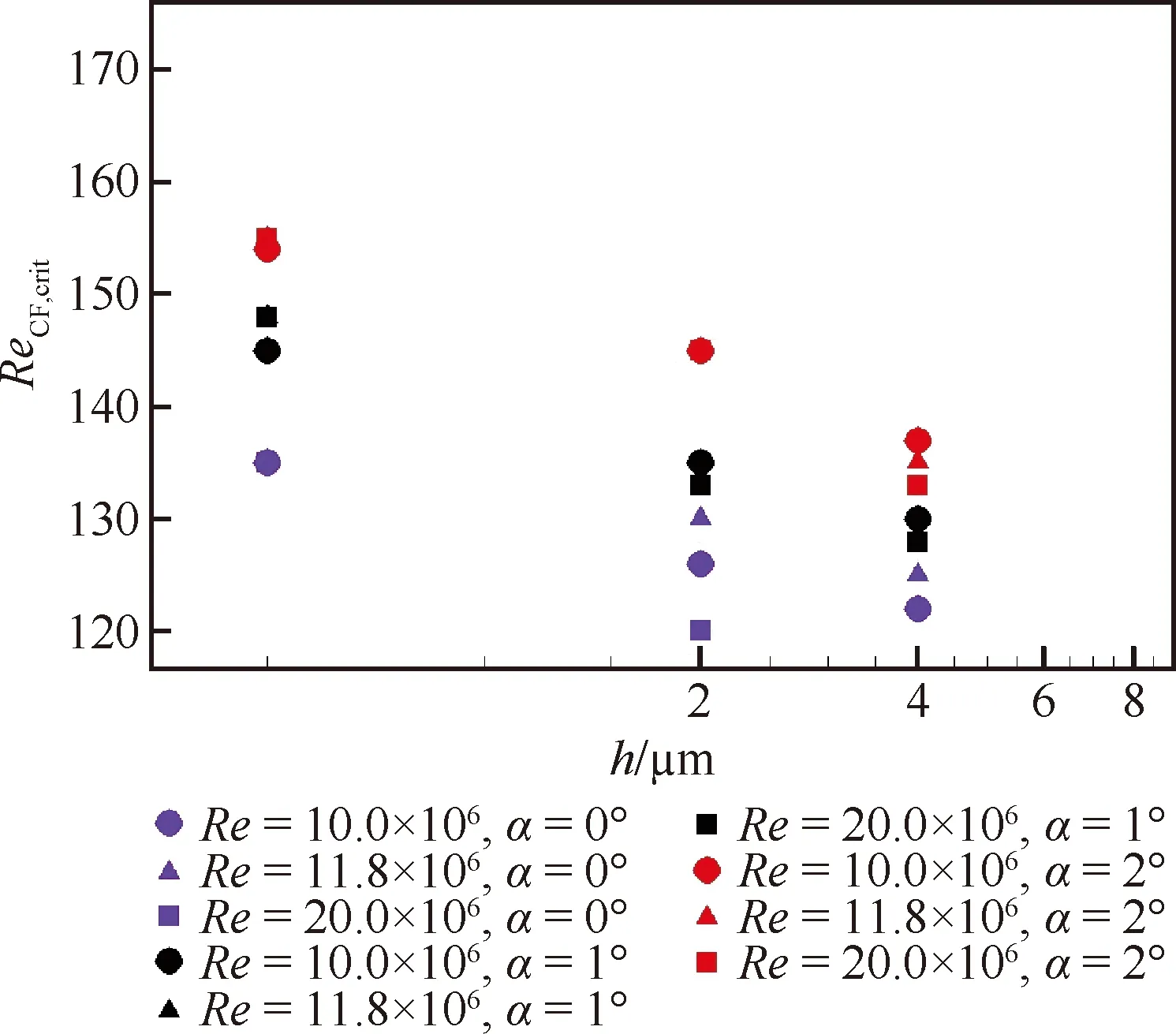
图7 椭锥转捩数据的稳定性拓展[17]Fig.7 Stability extension of transition data for elliptic cone[17]
基于图7[17]的数据与规律发现,参考低速横流转捩判据[12]的形式,采用表面粗糙度与无量纲涡量强度Hcrossflow实现判据当地化,构造了考虑表面粗糙度的当地化高超声速横流转捩判据:
(10)
式中:lμ为粗糙度参考高度,lμ=1 μm;CCF-1和CCF-2为系数,由最小二乘法获得,CCF-1=-9.618,CCF-2=128.33;f(Hcrossflow)为考虑横流强度的抬升函数。抬升函数以0°攻角椭锥数据为基准进行定义:
有人说“困难像弹簧,你弱它就强”,压力也不例外。在工作压力面前,校长如何自我调适呢?我认为多想多做,脚踏实地地朝着目标前行;与压力为伴,多修炼自身,多读书,读好书。在学校管理实践中,不断打磨自己,不断提高自己的工作素质和能力,才能出色完成学校的管理工作,从而减轻工作给自己带来的压力。
(11)
f(Hcrossflow)=6 000|0.106 6-ΔHcrossflow|+
50 000(0.106 6-ΔHcrossflow)2
(12)
式中:ΔHcrossflow和Hcrossflow分别为横流强度抬升项[12]和当地涡量强度。
2.4 基于γ-Reθ转捩模型的横流拓展
横流效应以源项形式嵌入到动量厚度雷诺数Reθ t输运方程中:
(13)
式中:DCF为源项,定义为

(14)

3 高超声速三维边界层转捩算例验证
在高超声速横流转捩判据建立完成后,对高超声速修正的γ-Reθ转捩模型进行了横流拓展,将改进后模型命名为C-γ-Reθ高超声速三维边界层转捩预测模型。基于该模型对高超声速尖锥风洞试验[14]和某飞行试验的多个状态进行数值模拟,验证了尖锥外形三维边界层转捩阵面形态。
3.1 带攻角锥的常规风洞试验
尖锥几何参数包括头部钝度、半锥角和长度。风洞试验[14]由中国空气动力研究与发展中心完成,转捩阵面由红外热图试验获得,来流马赫数Ma=6,雷诺数Re=1.0×107,攻角α=0°~10°。数值计算网格量为110万,物面第1层法向网格间距y+<1,来流湍流度为Tu∞≈0.8%,表面粗糙度h=0.2 μm。来流总/静温、总/静压等具体设置见文献[14]。采用粗、中、密3套网格(M1、M2、M3)进行网格无关性验证,网格量分别约为30万、60万、80万。如图8所示,热流区别主要集中在转捩发生后的湍流区域,M1差异较大,而M2与M3之间分布差异几乎可忽略不计。因此,采用中等网格M2开展进一步多状态计算。
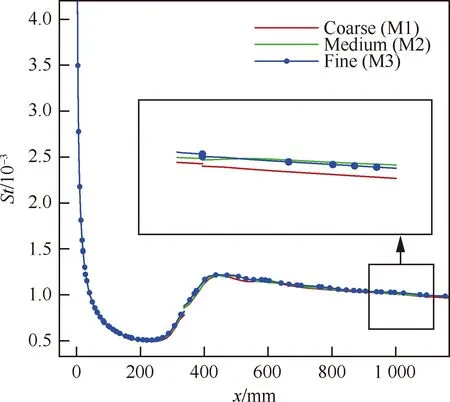
图8 α=0°时不同网格尖锥中心线St分布Fig.8 St distributions on center line for different grids of sharp cone at α=0°
图9为不同攻角下风洞试验热流分布[14]与数值预测结果对比,攻角依次为0°、2°、4°、6°、8°、10°。风洞试验测量为温升ΔT分布,模型预测为表征热流的斯坦顿数St分布,二者均可用于判断转捩位置。风洞试验和CFD计算中绿色区域为层流,红色区域为湍流,明显分界线为转捩。

图9 风洞试验[14]与C-γ-Reθ模型预测迎风面转捩位置对比Fig.9 Transition location comparison of wind tunnel experiment[14] and C-γ-Reθ model predictions on windward surface
由于模型预测的部分状态(α=2°, 4°)中心线转捩位置相对靠后,为完整观测转捩阵面形态,设置图8模型预测结果横坐标范围为[0, 900] mm,大于风洞试验观测窗口范围[0, 800] mm。由图9数值计算结果与风洞试验结果对比可知,构建的转捩模型能够较为准确地预测尖锥迎风面中心线Mack模态以及侧面横流不稳定性导致的转捩,转捩位置与三维转捩阵面整体形态都得到了较好的模拟,并且能够反映三维转捩阵面随攻角的变化趋势。大攻角(α=8°, 10°)下模型预测的转捩位置比试验结果更为靠前,可能的原因是大攻角下迎风面边界层较薄,表面粗糙度更易引起转捩。
3.2 带攻角锥的飞行试验
某圆锥飞行试验转捩段的飞行马赫数约为6,其转捩阵面由试验模型表面的分布式薄壁测温传感器测量得到。在该飞行试验的一定弹道范围内测得了清晰的转捩阵面随攻角和雷诺数的变化情况,且经过稳定性分析和相关测量数据分析,证明了飞行器表面横流转捩的存在。该横流流动由攻角引起的周向压力梯度造成。飞行试验测量的转捩数据和对应飞行状态可以用于验证C-γ-Reθ高超声速三维边界层转捩预测模型。
如图10所示,C-γ-Reθ转捩模型较好地模拟了带攻角圆锥飞行试验的横流转捩阵面。在不同飞行高度对应不同飞行状态下,圆锥±90°子午线附近区域转捩阵面呈近似对称状态,转捩模型计算的横流转捩阵面与飞行试验测量结果较接近。
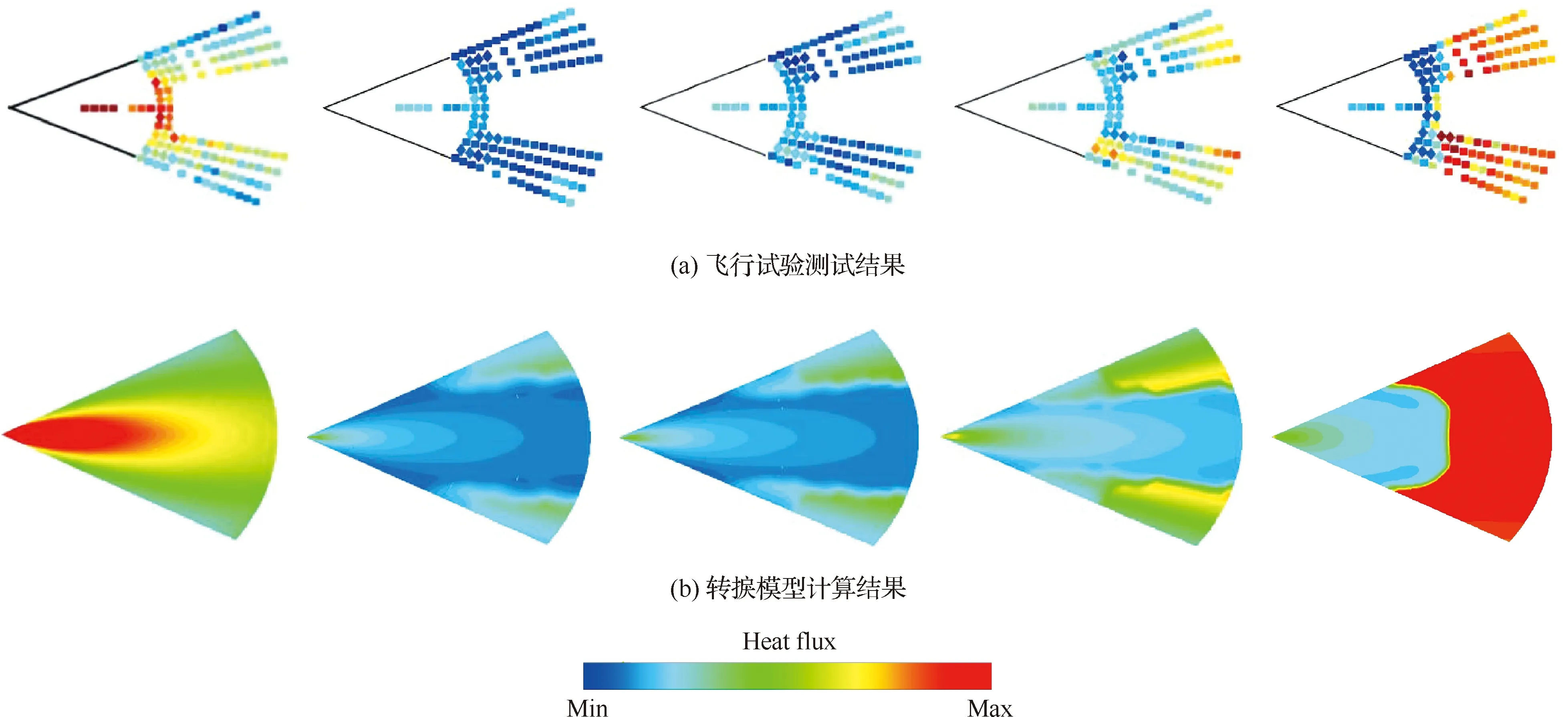
图10 飞行试验与C-γ-Reθ转捩模型表面热流分布Fig.10 Heat flux distributions on surface of flight test and C-γ-Reθ transition model
4 结 论
基于Chant 2.0高超计算平台的γ-Reθ转捩计算模块构造了高超声速横流转捩判据,进行了横流转捩模型拓展和验证,改进后的高超声速三维边界层转捩预测模型命名为C-γ-Reθ转捩模型。研究工作得到如下结论:
1) 利用已有的DNS计算数据,经过稳定性分析的eN方法拓展,获得了边界层转捩临界横流雷诺数ReCF,crit与表面粗糙度h和当地涡量强度Hcrossflow的函数关系,构造出当地化的高超声速横流转捩判据。横流判据的建立对于高超声速横流转捩模型的建立以及横流拓展具有重要意义。
2)C-γ-Reθ转捩模型在多个横流转捩测试算例中表现良好,计算结果与测量结果符合较好,模型基本能够模拟多状态下的圆锥风洞试验和飞行试验的三维边界层转捩阵面形态。
建立的高超声速三维边界层转捩模型是基于RANS方程的工程预测方法,对于横流不稳定性诱导转捩的高超声速边界层转捩预测具有一定的意义与价值。目前该模型仅在少数典型算例上进行了数值验证,下一步将在更多工况、更加复杂外形的高超横流转捩算例中进行测试与改进,进一步考核与提升该模型在工程应用中的适用性。
