单元起始课

黄娅丽

一、教材分析

本节课是高中数学北师大版必修1第二章《函数》的第一节内容，是本单元的章节起始课，为学生后面理解函数的概念做好铺垫，起到承上启下的作用，同时通过本节课的学习，从真实情景入手，学生通过提出问题、解决问题，从而建构本单元学习内容的结构框架，理清本单元要学习的主要内容及关系也是本节课的重点和难点。

二、学情分析

初中阶段，学生学习了一些简单的初等函数，如一次函数、正比例函数、反比例函数、二次函数等，学生对两个变量关系已经有了初步的认知基础，通过高一第一章《集合》的学习，学生对集合思想也有一定的认识，学生具有一定的分析、推理、抽象概括的能力，这些为这节课的学习打下了基础。

三、教学目标

1.能够在大情境中，提出问题，在解决问题的过程中发现和认识生活中变量间的依赖关系;

2.通过对生活及其他领域中变量关系的举例，认识依赖关系和函数关系，感受、领悟生活中处处有变量，变量之间充满了联系，提升学生的数学抽象和逻辑推理核心素养;

3.学生在爱心活动的真实情境中，提出问题、解决问题，问题层层递进，自然生成，师生共同建构本单元学习内容的结构框架，理清本单元要学习的主要内容及关系，对大单元的学习目的，学习意义，要学的内容的本质达成关联性理解，克服了以往零散化碎片化学习的缺点，对单元学习的数学知识有了整体性的认识，同时也渗透了本单元的学习方法， 培养学生发现问题、提出问题、解决问题的能力。

4.通过爱心活动的真实情境，既能解决数学问题，也能有积极的、正面的教育意义，并通过此情境激发学生的爱心、乐于助人、乐于奉献、社会责任感、社会担当等品质，渗透德育。

四、教学重点与难点

教学重点：生活中的变量关系，建构本单元的内容框架。

教学难点：通过真实情境建构本单元学习内容的结构框架，对本单元的知识有一个整体的认识。

五、教学方法：启发引导、讨论交流、合作探究与自主探究相结合的教学方法。

六、教学过程

（一）情境引入：

1.大情境

陕西省三原县东周儿童村是一家民间慈善机构，它是救助特殊困难环境下的少年儿童，儿童村无偿为入村儿童提供包括衣、食、住、行、医疗保健、读书上学、文化娱乐等一系列服务，给这些孩子提供一个生活、学习、健康成长的场所，帮助孩子们渡过生活难关。

一次偶然的机会，小华等3名同学也了解 “儿童村”的情况，内心感触很大，他们决定为这些孩子们做些什么，于是他们在班级募捐衣物或书籍或爱心捐款等，他们打算在儿童节这一天，带着这些物资去看望这些孩子们，和他们一起过一个不一样的儿童节。

设计意图：真实情境引入，引发学生思考，将生活问题数学化，并通过此情景引发学生的爱心、同情心、善良、乐于助人、社会责任感等渗透德育。

2.大任務

目前他们募捐了1655元爱心捐款，他们打算为这些孩子们购买一些需要的学习用品或生活用品，你能帮他们规划一下这次爱心活动吗？我们需要做哪些准备工作？

学生活动：前后4桌讨论交流2分钟，选出代表说出自己的想法，教师将学生们提出来的问题罗列出来。

预测学生会提出一下问题：（1）买什么？做预算;（2）怎么去？交通问题;（3）天气情况等

设计意图：学生通过讨论、交流，在实际情境中，发现问题、提出问题。

（二）提出问题、解决问题，建构本单元学习内容的结构框架

活动一：一套语文、数学、英语、作文、美术作业本批发价10元，书包批发价35元一个，将作业本及书包统称为学习用品，你能写出学习用品的套数x与购买费用y的关系式吗？

问题1：上面问题中哪些是常量？哪些是变量？

问题2：这些变量是什么关系？

问题3：据了解儿童村现有28名儿童，如果给每个孩子买一套学习用品，你能算算需要多少费用，还剩多少钱吗？

问题4： 请同学们回忆初中函数的定义

问题5：你能辨析下列变量之间的关系吗？

（1）路程与时间;（2）身高与体重;（3）桃子的重量和梨的大小。

由此得到：生活中的变量关系：

（1）函数关系--对于变量x的每一个值，变量y都有唯一确定的值与之对应。（确定关系）

（2）依赖关系--有关系，是一种不确定关系。

（3）非依赖关系--两变量之间没有关系。

问题6：你能说说函数关系与依赖关系的区别和联系？

是函数关系一定是依赖关系，是依赖关系不一定是函数关系。

问题7：请你举例生活中的函数关系和依赖关系？

活动二：小华等3人先坐地铁和公交到义合村，因为公交太少，剩下约8公里他们打算坐出租车，当地出租车的计费方式：一般普通出租车白天起步价为6元，起步里程2公里，超过起步里程数每公里1.5元;如果不计等待时间，你能写出出租车的费用y（单位：元）与行驶里程x（单位：公里）关系式吗？他们打车的费用是多少？

活动三：你能发现下面问题中函数关系有什么共同的特征吗？

设计意图：学生通过观察这些函数的共同特征，由此得到本单元要学习的幂函数。

问题8：y=1是函数吗？

设计意图：初中的函数是从运动变化的角度描述函数的，不能很好地解决如y=1是不是函数等问题，具有一定的局限性，因此高中我们需要从集合角度用对应来刻画函数，这种用集合语言定义函数更精确，研究函数的性质等更方便。

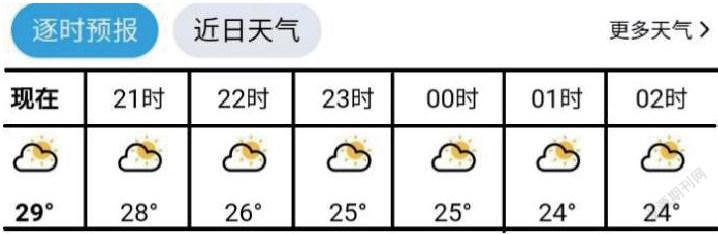
活动四： 去之前，我们要了解所去地方一天的天气和气温情况，根据天气预报，做好出行准备，下面表格表示的是某天整点对应的气温情况。

下图为某天24小时内气温随时间变化的曲线图：

问题9：你能根据图像，说出那一个时间段气温是上升的？哪一个是时间段气温是下降的？什么时刻气温最低？什么时刻气温最高？

活动五：观察下列函数的图像， 这两个函数图像有什么特征？

设计意图：由函数图像的增减性、对称性，引出本单元要学习的函数的单调性和奇偶性。

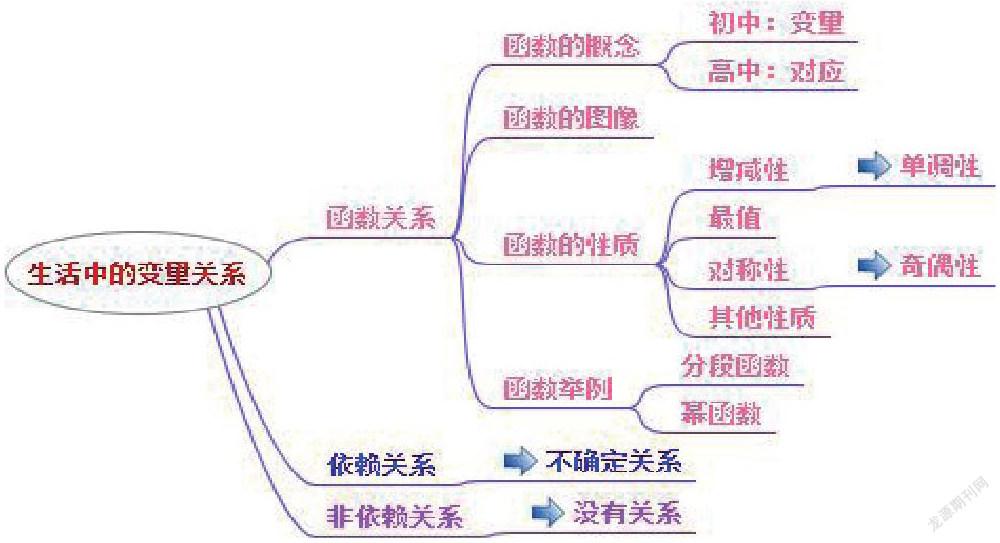
本单元学习内容框架：

（三）课堂小结： 谈谈你本节课的收获？

八、学生的自我评价

评价标准 得分

你能辨析生活中变量关系中的依赖关系与函数关系吗？ 5 4 3 2 1

你能说出函数关系和依赖关系的区别吗？

你能画出本单元的知识结构图吗？

九、作业设计

必做题：请你寻找并写出实际生活中的函数关系、依赖关系、非依赖关系（每种关系至少3个）。

选做题： 请调查你所在城市的出租车的计费方式，如果不计算等待时间，请你尝试写出出租车费用与路程之间的函数关系。