学习情境链创设视域下的计算思维培养模式

摘要：思维具有情境性，对思维能力的培养需借助于特定情境方能实现。然而，当前中小学计算思维教学中普遍存在情境创设浅表化明显、连贯性较弱和延展性不够等不足，难以有效促进学生计算思维能力的持续发展。创设情境要素多元且相互关联的学习情境链能有效避免学生在思维发展中的“跳跃感”和“断层”现象，有利于形成可促进其计算思维持续渐进发展的学习情境闭环。基于学习情境链创设视角所构建的计算思维培养模式，通过对递进式问题情境、支架式探究情境、互助式合作情境、平等化交流情境及延展性应用情境的创设，形成了计算思维“唤醒—激活—强化—升华”的培养闭环，有助于促进计算思维的螺旋式发展。该模式在以“递归算法——神奇的斐波那契数列”为主题开展的Scratch编程教学实践中的应用表明，其能够较好地实现对学生问题界定、特征抽象、算法设计、评估迭代和迁移应用等计算思维核心能力的培养。

关键词：计算思维;培养模式;学习情境链;Scratch編程

中图分类号：G434   文献标识码：A    文章编号：1009-5195（2021）05-0072-10  doi10.3969/j.issn.1009-5195.2021.05.008

基金项目：国家自然科学基金项目“民族地区优质数字教育资源均等化配置机制研究：系统动力学建模与政策仿真”（71764036）;云南省基础研究计划面上项目“数字教育资源精准服务模式及关键技术研究”（2019FB088）。

作者简介：杨文正，博士，副教授，硕士生导师，云南师范大学信息学院（云南昆明 650500）。

一、问题提出

随着计算思维内涵的逐渐明晰和外延的不断丰富，计算思维培养的实践方式也呈现出多样化发展趋势，但仍有其共同之处：强调将计算思维培养与生活实践接轨，将思维过程与技术工具结合，让学生在运用编程技术解决问题的过程中实现逻辑推理、抽象归纳、迁移应用等高阶思维能力的提升（孙立会等，2020）。编程教学以其在逻辑思维、算法设计和创新能力培养上的特有潜能成为计算思维培养的有效途径（傅骞等，2019）。可视化编程在保留算法核心思想的同时降低了学生的认知负荷，学生的学习兴趣得以提升并能留出更多的认知资源聚焦于计算思维的发展，更适合中小学生的认知水平（范文翔等，2018）。在信息技术课程教学中，常见的可视化编程工具有App Inventor、Scratch、Mixly等，其中Scratch编程软件技术门槛低，将抽象的语法规则、算法结构蕴藏于积木式的图形化语言中，大大降低了学生的认知负荷水平，成为中小学教师开展编程教学的主要工具。

皮亚杰的发生认识论认为，思维是在主体不断迭代的逻辑运演中动态生成的，当学习者的认知结构发生逻辑冲突时，便可以通过对图式的重构来触发思维的螺旋式发展（林琳等，2019）。这种思维结构的丰富性不仅要求学习者融入到特定学习情境中，更需要教师挖掘特定学习情境之间的关联性，创设有助于思维培养的学习情境生态闭环。在计算思维培养过程中，有效的学习情境创设可以“挑起”学生的认知冲突，激发学生不断通过更高级的逻辑运演领会计算机解决问题的思想、原理与方式。

然而，当前中小学计算思维教学中的学习情境创设仍然存在诸多不足：（1）与学生实际生活联系不够紧密。有些学习情境的选择过于拘泥于教材，未能与学生熟知的生活现实紧密贴合，未能阐明问题解决在实际生活中应用的价值。（2）问题情境挑战性不足。教师所创设的问题情境有明确的指向性，这在一定程度上易于引起学生参与编程学习的兴趣，但复杂性、挑战性不足的问题却可能使学生的持续性思考与探究难以维持。（3）学习情境创设连贯性较弱。多数情境创设只存在于教学的引入部分或嵌入在某一教学活动片段中，未能将情境学习理念贯穿于编程教学过程的始终。（4）学习情境创设浅表化。有些学习情境创设未能将多元情境要素与计算思维培养过程有机融合，导致学生对算法原理和信息技术学科核心素养的思考停留在浅表层面。（5）学习情境创设的延展性不强。能够促进学生协作开展知识构建的开放式交互情境设计不多，计算思维迁移应用场景增拓较少，不利于学生思维活动的深化。

思维具有情境性，思维能力的培养不能脱离真实情境。如何挖掘与计算思维培养活动相适应的多元情境要素？如何构建各类情境要素优势互补的协同机制，发挥其对学生思维能力发展的协同效应？这既是计算思维教学的实践诉求，也是中小学校信息技术课程教学改革的内在需求。针对在计算思维教学中学习情境创设存在片断化、单一化和浅表化等问题，本研究提出学习情境链创设的新思路。学习情境链创设可以弥补多元情境教学中情境创设不连续、片断化的不足，削弱孤立、零散的情境元素给学生认知和思维发展造成的“跳跃感”和“断层”现象，有利于形成计算思维渐进发展的实践场域。本研究基于对计算思维概念的解构和情境学习理论核心要义的剖析，阐明学习情境链的内涵，进而依循项目式教学基本流程，构建基于学习情境链创设的计算思维培养模式，最后以“递归算法——神奇的斐波那契数列”为主题开展Scratch编程教学活动，旨在探索多元情境要素与计算思维核心能力培养耦合的实践途径，为计算思维培养教学实践提供范例。

二、理论依据

1.计算思维概念解构

周以真教授认为，计算思维是运用计算机科学的基础概念进行问题求解、系统设计以及人类行为理解等的一系列思维活动（Wing，2006）。国际教育技术协会和计算机科学教师协会（ISTE et al.，2011）共同为K-12教育中的计算思维下了操作性定义，认为计算思维是解决问题的过程，通常包括：能够使用计算机或其他工具来解决问题;有条理、有逻辑地分析和组织数据;将数据进行抽象，并通过模型来表示;运用算法和程序设计自动化解决问题的方案;试行方案和对方案进行优化或完善，并在实施过程中实现资源有效整合;对问题解决过程进行概括，并进行迁移应用。英国学者Selby等（2013）通过文本分析方法总结出计算思维具有抽象、分解、算法思维、评估和概括五大特征。我国《普通高中信息技术课程标准（2017年版）》明确提出了计算思维培养的要求：通过抽象的方式（如模型、模拟）表示数据;设计算法形成自动化解决问题的方案;总结解决问题的一般过程与方法，并迁移至更宽泛的问题解决中（中华人民共和国教育部，2018）。吴忭等（2019）认为，计算思维并不是单一的认知技能，而是“专业概念”“专业实践”和“专业认识”多方能力维度的有机结合。

基于以上对计算思维概念及特征的分析，本研究认为计算思维是利用计算机科学领域的思想、原理、方法解决实际问题的高阶思维能力，并将其解构为更具操作意义的五大核心能力：界定问题能力、抽象特征能力、设计算法能力、评估迭代能力和迁移应用能力。界定问题能力是指学生在教师创设的问题情境中发现问题并进行需求分析，从而区分问题边界，明确学习任务的能力;抽象特征能力是指能提取问题的关键特征，并用形式化的方式表征问题的能力;设计算法能力是指选择合适算法设计问题解决方案，并用编程语言等数字化工具实现方案的能力;评估迭代能力是指依据信息系统设计的普遍原则对问题解决方案进行全面评估和迭代优化的能力;迁移应用能力是指总结问题解决的一般过程与方法，并应用于解决学习、生活中的其他相关问题的能力。计算思维五大核心能力的发展过程就是从界定问题到解决问题的路径迭代，体现出学习者在逻辑运演中不断拓展和丰富思维结构的发展过程。“促进计算思维，培养编程能力”作为中小学信息技术课程的核心目标，不仅要让学生能夠理解信息系统工作原理，而且要让学生学会计算机科学的核心概念和方法，培养其抽象与逻辑思考、系统化思考等思维能力（张进宝等，2018）。

2.学习情境链内涵解析

尤尔根·哈贝马斯（Jürgen Habermas）认为，人的理性总是嵌入在具体事件当中，知识的加工正是在这种情境理性的氛围中发生的（尤尔根·哈贝马斯，2004）。情境学习理论提出了关于学习的新观点：“思维和学习只有在特定的情境中才有意义”“不存在非情境化的学习”“学习是合法的边缘性参与”“学习是社会协商”（戴维·H.乔纳森，2002）。情境学习理论的核心要义是让学习者进入与专业领域相关的真实情境，在教师的指导下参与学习共同体活动，在合作协商、探究反思和解决问题中潜移默化地习得默会知识和思维技能。心理学领域的情境认知理论强调“个体参与‘实习场中的情境活动以建构知识”;人类学领域的情境学习理论强调“个体通过合法的边缘性参与实践共同体获得意义和身份的建构”。在编程教学实践中，“实习场”的设计就是要让学生进入结构不良和具有挑战性的真实问题情境中，运用编程工具体验计算机解决问题的原理和方式;“实践共同体”的创建强调学生在共同的项目任务下组建学习共同体，通过合作探究、经验互动和意义协商解决实际问题。二者都聚焦在计算思维与问题情境之间建立联系，创设有助于驱动学生参与知识建构和融入社会协商的开放式交互情境，对提升学生编程兴趣和发展其计算思维具有显著意义（张进宝，2019）。

思维发展是分阶段或分步骤的演变过程，计算思维也是阶段性提升的，其遵循螺旋式发展的规律（孙立会等，2020）。学习情境与计算思维培养过程紧密关联，学习情境设计要遵循计算思维发展的逻辑结构，以“链”式样态有序关联各情境要素，形成促进计算思维能力发展与品质升华的学习情境链。本研究所指的学习情境链是以多个相互关联的情境为“节点”，随着教学活动的动态发展，将多元情境要素有机联接，形成连贯有序的情境环路。学习情境链创设就是要在教学过程中，围绕教学主题设计多元学习情境要素，让各要素沿着计算思维教学环节逐级“流动”，形成优势互补、协调发展的学习生态系统，最终形成有利于学生计算思维渐进发展的闭环，触发思维品质的升华。

基于此，本研究从情境学习理论的核心要义中抽取出了问题情境、探究情境、合作情境、交流情境、应用情境5个情境要素，探寻其贯穿于教学过程中的隐含线索和相互作用，创设有利于学生计算思维发展的学习情境链。问题情境应当充分生活化，激发学生解决问题的需要，提升其对学习任务价值的认可，从而调动内部动机（赵国庆等，2018）;探究情境是指在教师的支持下，学生围绕项目任务制定计划并开展自主探究活动的场域;合作情境强调创建氛围良好的学习共同体，促进同伴合作交流、知识协同发展;交流情境旨在为学生创造展示探究成果的平台与机会，实施过程性评价，驱动项目作品的迭代改进;应用情境的创设应积极挖掘教学内容与学生生活经验之间的关联，发展解决新问题的迁移能力。学习情境链与计算思维核心能力之间是典型的耦合关系。学习情境链是由多个异质性情境要素构成的学习环境系统，通过学习情境“节点”之间的情境要素“流动”，增强项目式编程教学活动中学习的交互性，实现计算思维核心能力发展。

3.多元情境教学应用引鉴

美国教育家约翰·杜威（John Dewey）认为，思维是从直接经验开始的，人们只有沉浸于不确定的情境中，才能引起积极探索与思考的强烈动机（约翰·杜威，2011）。著名教育技术学者戴维·H.乔纳森（David H. Jonassen）认为，情境是指能够作用于人的思维并引起情感变化和行为活动的时空环境，具有复杂性、真实性和多样性等特点（戴维·H.乔纳森，2002）。学习情境对学习者知识建构、思维启迪、情感体验等方面的促进作用成为人们的共识，多数学科教师在教学实践中积极尝试创设多元学习情境以促进学生认知和思维发展。例如，针对地理学科特性，姜乔（2019）提出了融合“直观情境、问题情境、合作情境、探究情境和生活情境”等地理多元情境的教学模式;针对通用技术三种课程类型（技术理论课、技术绘图课、技术制作课），郑瑶瑶（2014）设计了“应用情境”“问题情境”“媒体情境”“语言情境”等学习情境要素，并交叉运用在“情境准备”“情境创设”“情境展开”“情境深入”和“情境提升”等环节的教学过程中。其共同点在于：情境创设紧密贴合学科课程标准和学科思维特性，对教学内容进行横向拓展或纵向挖掘;认为有效的学习情境应具备生活性、真实性、探究性、情感性和可变性等特征;多元学习情境设计旨在唤醒学生的已有经验，在自主或合作探究解决真实问题的过程中激活学生的思维，提升思维品质。

然而，多数学科教学中创设的学习情境彼此孤立，多元情境要素之间关联性不强，未能构成一条贯穿于教学过程始终的连续回路，这势必影响思维发展阶段的衔接与黏合。学习情境链以多元情境要素为节点，前后衔接的两个情境要素组合成一个链节，多个链节首尾相连，从而形成闭合环路，以此弥补多元情境教学中情境创设单一、不连续的问题。作为课堂教学一以贯之的情境主线，学习情境链创设可以在很大程度上削减孤立零散的情境要素给学生认知发展造成的“跳跃感”和“断层”现象。学习情境链创设对编程教学活动中计算思维的培养具有明显的启迪、激活、强化和升华功能：问题情境创设能唤醒学生的前概念，以富有挑战性的复杂问题触发学生的认知冲突，引发思考的强烈欲望，让学生在情境感知中启迪思维的火花;教学活动中的多元化学习情境创设可以从不同层次、多个侧面挖掘学习资源，持续激活学生思维、塑造整体认知环境;创设开放的学习情境能为学生提供计算概念再现的实践场域，在迁移应用过程中强化其对计算思维内涵的理解;依循学生思维渐进发展的规律创设连贯的学习情境，既有助于学生将零散的知识串联，又可以保持连续、平滑的思维发展过程，促成计算思维的升华。

三、模式构建

编程教学活动中蕴含了大量难以用语言清晰描述和直接传授的“主观知识”和“实践情境知识”（郑浩等，2017）。学生只有在不同的情境脉络中运用复杂的思维技能进行问题求解，才能深度理解“隐形”于编程语言环境中的计算思维（姜强等，2020）。学习情境链创设有助于学生在编程教学中实现思维活动的外显化、趣味化和深度化。学习情境链创设强调情境对学科知识意义建构和迁移应用的独特作用，注重学生在情境感知、实践操作和亲身体验中提升学科素养。真实性是构建一切情境要素的基础，各类情境要素的设计应以贴近学生生活经验为导向，使个体从自身经历的角度来诠释和建构知识（欧阳忠明等，2018）。创设贴近真实世界的学习情境有利于还原学科知识的产生过程，阐明学科知识的应用价值，满足学科核心素养的发展诉求。各类情境要素不是彼此割裂的，而是相互联系、交叉和融通的，教师应根据教学实际情况和学生的原有认知水平，优化组合各类情境要素，形成学习情境链。学习情境创设要贯穿于编程教学过程的始终，各情境要素间应体现出一定的连续性、层次性和深度性，让学生在递进式的情境化教学过程中逐渐深化计算思维。

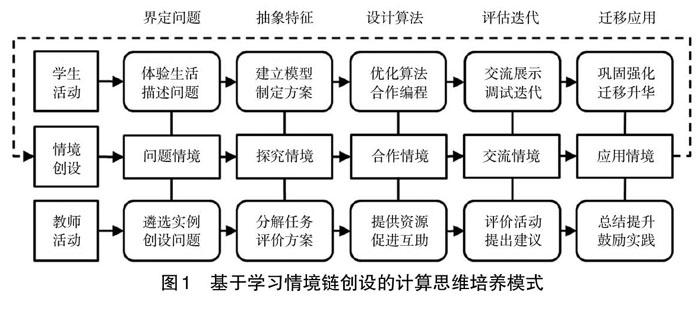
为探索多元情境要素与计算思维核心能力培养耦合的实践途径，本研究针对中小学校编程教学实践中的情境创设问题，依循项目式教学基本流程，构建了“基于学习情境链创设的计算思维培养模式”（如图1所示）。该模式以问题情境创设为出发点，将探究情境、合作情境、交流情境、应用情境融入教学活动全过程，形成各情境要素之间灵活组合、有序衔接和循环流动的学习情境链。该模式的关键是将计算思维五大核心能力的培养附载于学习情境链的动态生成过程中，师生在每一情境节点上充分交互，教师通过调节教学活动，促使学生计算思维得到充分发展。这具体体现在如下几个方面：基于学生生活经验的真实问题创设问题情境，让学生在感知体验和独立思考中界定问题能力得到发展;创设探究情境，为学生提供学习支架，辅助学生抽象出复杂问题的特征;创设合作情境，为学生参与学习共同体、共享算法设计和互助合作编程提供环境支撑;创设交流情境，鼓励学生积极展示成果，通过自评、互评等多种表现性评价手段促进程序算法的迭代优化;挖掘应用情境，引导学生将自动化、系统化解决问题的能力迁移应用到新的问题情境中，由此再次引发学生持续运用计算思维解决挑战性更强的现实问题。

思维发生在过程之中，计算思维发展的轨迹呈现出由低层次结构样态向高层次结构样态迭代演进的“非线性”逻辑脉络（张沿沿等，2020）。学习情境链中的多元情境要素遵循计算思维发展的内在逻辑，将彼此关联起来，以非线性、动态迭代的方式灵活地嵌入在项目教学活动之中，以促进计算思维结构向更高层次发展。计算思维核心能力与学习情境要素在动态耦合中相互作用、螺旋上升、协同发展。例如，界定问题能力既可在问题情境创设中培养，也可以在探究情境、合作情境、应用情境等各类学习情境中得到发展。教师预设挑战性问题情境，支持学生联系生活实际，回溯原有知识结构，拓展前后知识间的逻辑关联，从而促进界定问题能力发展;学生在探究性学习情境中及时改进项目设计方案，重新审视问题界定的准确性;小组成员在良好的合作情境中反复测试程序、优化算法，不断在试错中发现问题并设计新的程序方案;在新的应用情境中，学生重新思考作品的现实意义，针对新的生活场景迁移应用成果，拓展问题边界，再次界定问题。与此同时，问题情境也不仅限于培养学生的界定问题能力，还能为其他核心能力发展提供支持。例如，学生依托问题情境快速投入到体验式学习活动中，借助生活实例将客观事实内化为知识，在克服认知冲突中逐渐明晰问题域，提升界定问题能力;通过创设问题情境可以启发学生提取先验知识，概括问题关键特征并对问题进行形式化表达，使其抽象特征能力得到发展;在编程测试环节设置问题情境有助于引导学生共同协作，优化算法并进行编程实现，从而培养学生的设计算法能力;在交流评价环节中创设问题情境，可以提升学生问题意识，使其针对小组自评或互评的反馈建议，迭代完善项目作品;学生在新创设的问题情境中再次反思项目成果的实际应用价值，灵活运用编程知识与技能解决新问题，从而提升迁移应用能力。

下文以学习情境要素为切入点，从递进式问题情境、支架式探究情境、互助式合作情境、平等化交流情境和延展性应用情境创设方面，阐述如何通过学习情境链的创设促进学生计算思维发展。

1.递进式问题情境创设

问题情境以结构不良、真实的生活问题为中心，促使学生在与真实情境发生互动时产生认知冲突，从而激发创造性解决问题的内驱力。在编程教学中，教师结合教学目标和学生经验，通过引入真实生活案例或组织实地参观等方式创设问题情境，引导学生在观察体验中自主发现问题，明确任务主题，从中培养界定问题的能力。此外，教师通过提问引导学生总结回顾算法设计的核心思想，重新思考探究成果投入现实生活中的应用方式，使其在新的问题情境中加深对算法思想的理解，实现迁移应用能力的提升。在初步感知问题和再次迁移应用的递进式问题情境创设中，学生将计算思维逐步“渗入”自身的知识结构。

2.支架式探究情境创设

探究情境旨在为学生提供学习支架，辅助学生抽象出复杂问题的特征，并运用算法设计解决问题的方案。在编程教学中，教师引导学生运用流程图和思维导图等认知工具抽象问题特征、分解问题求解步骤、建立数学模型以及自主设计问题解决方案，从而促进抽象特征能力的发展。同样，小组成员借助伪代码、自然语言和案例资源等认知工具，合作探究算法设计过程，比较算法执行效率，优选算法策略和编写程序脚本，最终实现设计算法能力的提升。支架式探究情境的创设不仅有助于拓展探究活动方式和延伸探究活动时间，还有利于抽象特征能力与设计算法能力的衔接发展，在充分尊重学生探究兴趣的基础上促进计算思维培养的逐层深化。

3.互助式合作情境创设

学生围绕特定任务在学习共同体中共享算法设计过程，互助实现编程，以此实现学科知识的意义建构和学科思维的深度培养。在编程教学中，教师通过创建互助小组，引导组内学生明确任务分配;组长带领组员探究各自主导的任务领域，反思优化算法，协作完成编程任务，逐步培养算法设计能力。在完成程序设计作品之后，教师组织形式多样的评价活动，为小组成员合作讨论程序设计过程和交流分享算法设计经验提供交互平台;学生在交流展示和优化程序的过程中，其评估迭代能力得以提升。合作情境让学生在合作协商中经历“设计算法—编写程序—交流评价—迭代程序”螺旋式上升發展过程，潜移默化地达成培养设计算法能力的目标。

4.平等化交流情境创设

平等化的交流情境鼓励学生积极展示成果，通过自评、互评等多种表现性评价手段促进程序的迭代优化。学生在编程教学的多样化评价活动中，展示程序设计作品，分享项目活动收获，听取师生评价建议和迭代改进程序设计。灵活设计的评价活动不仅能培养学生的评估迭代能力，还有助于锻炼学生的沟通表达能力。交流情境不只限于总结性评价活动，更体现在过程性评价活动中。教师应在学生制定好算法设计方案后及时组织评价活动，对学生的问题特征进行分析，针对数学建模思路和程序流程图设计的准确性提出反馈建议，帮助学生修改完善问题解决方案，从中培养其抽象特征能力。

5.延展性应用情境创设

应用情境强调的是知识在结构不良的、复杂的新问题情境中有效迁移和整合应用（王美等，2018）。在编程教学中，学生在总结算法思想的基础上，思考如何迁移算法思维来解决实际生活中的其他问题，探讨成果如何应用于日常生活以满足用户需求，在此过程中不断培养迁移应用能力。同时，教师应设计贴近学生生活经验的案例资源或项目活动，引导学生回归问题产生的逼真情境，再次培养学生的界定问题能力。应用情境的创设将探究问题的产生和算法思想的应用还原到真实情境中，鼓励学生在实践应用中重新发现问题，生成新的探究主题，探索解决新问题的思路。

四、应用案例

1.案例背景简介

案例以“递归算法——神奇的斐波那契数列”为主题，依托YN省KM市某中学高中二年级Y班“信息技术”课程中“算法初步”选修模块展开。教学对象已习得迭代、分治、动态规划等算法初步知识。本案例的教学三维目标是：在知识与技能方面，了解斐波那契数列中蕴含的递归算法思想，知道递归算法的基本特征;在过程与方法方面，掌握测试算法效率的方法，比较递归算法与其他算法的优劣，尝试优化递归算法，并能用Scratch编程实现算法;在情感态度与价值观方面，在优化算法和解决问题的过程中体会运用算法解决问题的优势，体验图形化编程的乐趣。案例教学流程依据本研究所构建的“基于学习情境链创设的计算思维培养模式”设计，围绕5个项目活动展开，分6个课时完成。在活动实施过程中，教师充分创设问题情境、探究情境、合作情境、交流情境和应用情境，并将其灵活组合应用于教学过程。

2.教学过程中的学习情境链创设

（1）创设问题情境，引导界定问题

此环节旨在创设真实问题情境，激发学生科学探究的兴趣，在发现斐波那契数列规律中发展界定问题能力。在每个项目活动开始之前，教师向学生发放植物观察记录表，告知学生观察校园植物时对植物的花瓣和叶片数量进行记录。学生实地观察校园种植的花草树木，根据记录表的要求记录植物名称、植物的花瓣或叶片数量，并进行拍照记录。在实地观察结束后，教师组织学生分享观察结果，并将统计好的数据展示出来，供学生寻找规律。期间，教师提问：“同学们看这组数列‘1，1，2，3，5，8，13，…发现什么规律了吗？”有学生随即回答：“自第三项开始，每一项等于前两项之和。”这时教师结合教学视频和课件向学生介绍斐波那契数列在自然界和数学、工业设计等领域的广泛应用。此后，教师继续发问：“当你在爬一个十级的楼梯时，每次可以选择爬一级或两级，请问一共有多少种爬法？”学生XL说：“如果爬两级楼梯，我有两种方案——可以先一级一级地爬，或者一次爬两级。”教师顺势引导：“那么爬五级、十级呢？”学生们开始在草稿纸上进行推导演算，最后发现爬楼梯问题的答案与斐波那契数列规律类似。教师总结：“推导演算的方法是运用数学思维来解决问题，人工运算较为耗时低效，那么如何通过Scratch编程来提高问题解决的效率呢？”

（2）运用探究情境，抽象问题特征

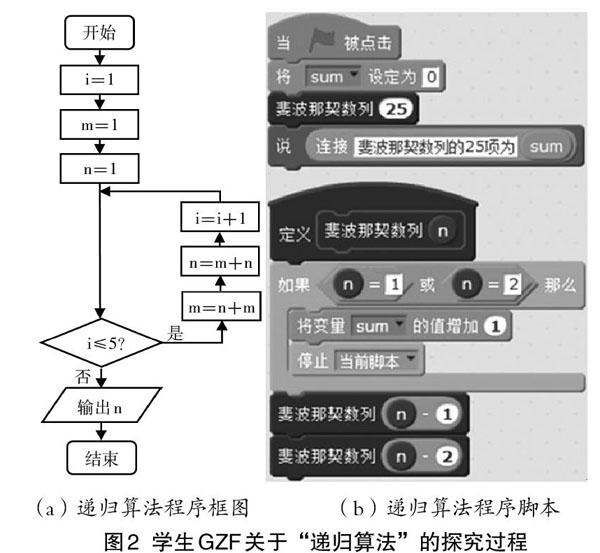
教师以程序流程图等为中介，创设科学探究情境，鼓励学生运用数学模型提取和表征爬楼梯问题的关键特征，并应用Scratch编程语言实现，发展抽象特征能力。经过教师对递归算法的讲解，学生认识到递归算法的核心思想是问题分解，即根据求解问题寻找递归体和结束条件。在灵活运用相关数学知识的基础上，学生自主探究爬楼梯问题的数学模型。期间，教师对学生数学建模遇到的困难进行引导。例如，学生GZF在寻找斐波那契数列的递归体时遇到了问题，教师快速对其进行引导：“回忆一下斐波那契数列的规律是什么？”学生GZF回答：“从第三项开始，每一项是前两项之和。”教师继续提问：“假设走法数为F（n），楼梯数为n，用函数公式怎么表达前两项之和？”经过教师的启发，学生GZF明白了递归体就是要找出原问题F（n）与子问题F（n-1）的递推关系，即F（n）=F（n-1）+F（n-2），n≥3。随后，学生采用绘制程序框图的方法，自主设计解决爬楼梯问题的程序框图，如图2（a）所示。教师设计过程性评价活动，组织学生分享自主设计的程序框图，引导学生互评，发现哪些算法设计更简洁、高效，最后提出算法改进建议，并让学生初步尝试编写递归算法程序脚本，图2（b）是学生GZF设计的程序脚本。

（3）营造合作情境，设计最优算法

此环节通过营造良好合作的学习氛围，促使小组分配任务和互助解决难题。教师以引导者、组织者和支持者的角色帮助学生循环测试和迭代优化算法。学生在教师指导下以组长负责制形式组建合作小组。教师给予学生充分思考和探究的时间和试错机会，在适当时机对学生提出的疑惑进行指导。小组成员根据自身优势进行任务分配，每位学生作为部分任务的主要负责人，带领其他成员完成小组任务，共同推进项目的实施。例如：A组学生JZY的主要任务是将程序框图转换成伪代码，学生DL用自然语言检查递归算法程序脚本的正确性，学生LB编写程序，学生WJ调试和改进程序。在将程序框图转换成伪代码的过程中，学生JZY发现有同伴不知道伪代码的概念，便利用教师提供的“导学案”进行讲解，帮助其突破学习难点;在组织同伴调试程序的过程中，学生WJ通过演示操作向同伴讲解自己擅长的调试策略，实现与小组成员的知识共享;在合作完成程序编写之后，学生LB和学生WJ发现随着输入项数增多，程序执行结果的输出时间就越长，这让他们意识到用递归算法实现的程序设计并不是最高效的解决方案。待全班大部分学生发现这个问题时，教师运用课件向学生讲解计算算法时空复杂度的方法。之后，A组学生合作计算出用递归算法解决爬楼梯问题的时空复杂度为T（n）=T（n-1）+T（n-2）+O（1），又通过树形结构表示算法执行过程，发现这种自顶向下的递归算法重复的结点数会随着n的增大而急剧增多，說明递归算法的运行时间是以n的指数递增，算法设计还存在优化的空间。

随后，教师引导A组学生思考，运用其他算法策略是否可以提高程序执行效率。经过小组头脑风暴，学生LB提议：“我们可以逆向思考，用自底向上的思路设计算法，这样程序重复调用自身的次数就会大大降低。”学生JZY表示：“可以用之前学过的迭代算法或动态规划算法尝试设计。”学生DL运用动态规划算法将问题分解为“楼梯数为1”“楼梯数为2”和“楼梯数大于等于3”三种情况进行求解，程序设计脚本如图3（a）所示。学生LB发现动态规划算法虽然可读性强、容易实现，但是程序变量设置和语句嵌套过于繁琐。他使用赋值语句并采用循环迭代的思想，对动态规划算法程序设计进行简化，如图3（b）所示。此时，学生WJ发现，虽然迭代算法设计的程序执行效率高、代码简洁，但仍然使用了4个变量。对此他提出使用链表结构对多个变量进行存储，既可以提高程序执行效率，还能将楼梯数n对应的每一项走法数F（n）呈现出来，如图3（c）所示。经过小组成员的协商讨论，决定选用链表结构实现的程序脚本作为最终程序设计作品。

（4）共创交流情境，评估迭代程序

该环节注重创建交流情境，促进师生以游戏化的形式开展小组自评、组间互评和教师点评活动，反思迭代程序作品。小组合作完成编程后，教师组织“算法效率大比拼”游戏，以检验程序执行效率。游戏规则要求教师和一名学生分别担任裁判员和计时员，各组抽签决定比赛顺序和对手组别。在游戏活动过程中，参与比赛的小组在裁判员宣布输入某一具体楼梯级数后，同时点击绿旗开始运行程序，计时员将两组程序运行时间记录下来进行比较。随着比赛的深入，裁判员会逐渐增大输入楼梯级数的数值，各组程序的执行效率差异也会更加明显。游戏活动通过3轮比赛决出冠亚军小组。最后，教师邀请各组交流分享算法设计经验和项目活动收获，组内成员和组间成员对程序设计作品进行评价。教师对每组程序设计作品进行点评，小组成员再次改进程序设计作品，将作品上传至Scratch社区供更多的编程爱好者讨论。

（5）挖掘应用情境，促进迁移应用

教师引导学生回顾运用递归算法求解问题的过程，通過提问启发学生总结分享递归算法的核心思想，并引发学生思考斐波那契数列在现实生活中的广泛应用，提升学生的迁移应用能力。例如，学生WJ认为：“递归算法的核心在于问题分解，通过数学建模将大规模问题分解成若干小规模问题，直至找到终止条件，然后再通过回溯逐个解决小规模问题，最后大规模问题也就迎刃而解了。”为拓展任务情境，教师播放介绍黄金分割法则的教学视频，引发学生思考，让其发现更多斐波那契数列在日常生活中的应用事例。学生WHS分享观点：“蕨类植物的叶片生长顺序也体现了神奇的黄金分割法则。”学生YL认为：“除了自然界，在艺术构图时也会运用到黄金分割法则，比如《蒙娜丽莎的微笑》。”讨论结束后，教师让学生回归日常生活，运用黄金分割构图法拍摄生活中的美景，并通过摄影展的形式组织学生分享。

3.教学反思

这一基于学习情境链创设的计算思维培养教学案例综合呈现了真实、连续和丰富的多元学习情境要素，其在教学目标上强调学生要追溯问题情境中算法产生的规律，以抽象化、形式化思维对真实问题进行描述，比较同一问题解决的不同算法效率。算法设计作为计算思维培养的重要组成部分，是信息技术教学的重点，也是本案例需要突破的难点。算法知识专业性较强，将情境教学法渗透到教学全程中可以有效避免单纯讲授知识点所带来的枯燥乏味感。教师将优化组合和进阶式设计的思路应用于学习情境链创设中，挖掘递归算法的应用场景，生成驱动性和挑战性强的探究问题;采用支架式教学策略，为学生“从始源情境（受客观条件制约的现实世界）向目标情境（有利于学习者知识建构的情境）转化”提供支持（王志军等，2019）。在教学实施过程中，教师采用项目式教学形式，将学习任务置于多元学习情境中，注重学生参与编程活动的体验而非仅限于问题解决的结果。教师引导学生在问题情境中表征递推关系;在探究情境中设计合适的算法并体验算法效率的差异;在合作情境中依托情境资源协同探究递归算法的优化方法及其编程实现;在交流情境中以游戏竞赛方式开展评价反思活动;在应用情境中拓宽递归算法的应用范围，形成用算法思维解决实际问题的迁移能力。面对不同的教学目标与学习任务，学习情境链呈现出对教与学过程的动态调节和链接作用，各情境要素协同促进教与学活动的有效进行，由此形成思维“唤醒—激活—强化—升华”的学习情境闭环（田阳等，2020）。

五、结语

思维的迸发需要情境的熏陶，连续的情境创设有助于锻炼思维的敏捷性、灵活性、独创性和深刻性，促进思维内在品质的升华。计算思维作为信息技术学科核心素养的重要组成部分，能让学生体验利用计算科学的基本概念和方法，进行问题求解、系统建构和人类行为理解的心智活动（陈鹏等，2018）。当前，多数编程教学实践还难以摆脱纯粹认知活动的缺陷，未能从“去情境化”走向学生丰富的“生活世界”，从“单一情境”走向“多元情境”，从“片断情境”走向“连续情境”。如何创设具有探究性、生成性、连续性和延展性的多元情境要素，是有序增进学生计算思维螺旋式发展的着力点。本研究提出的学习情境链创设，以设计环环相扣、逐次递进的多元情境要素为核心，形成思维“唤醒—激活—强化—升华”的培养闭环，为计算思维培养教学提供良好的启迪;构建的“基于学习情境链创设的计算思维培养模式”厘清了计算思维与多元情境要素的耦合关系，为计算思维培养实践提供了新思路。学习情境链有助于学生在思维活动与情境之间建立关联，促进学生思维品质的迭代升华。智能时代人们对计算思维培养寄予很高期望的同时，智能技术也将为计算思维培养创建更佳的学习情境，增强学习者的真实学习体验，促进学习情境达到“真实化”“个性化”和“精准化”（兰国帅等，2020）。如何利用新兴智能技术赋能情境学习，从而为中小学生计算思维培养和测评提供有力支持，这将是后续研究的焦点。

参考文献：

[1][美]戴维·H.乔纳森（2002）.学习环境的理论基础[M].郑太年，任友群.上海：华东师范大学出版社：63，65-67.

[2][德]尤尔根·哈贝马斯（2004）.理论与实践[M].郭官义，李黎.北京：社会科学文献出版社：15.

[3][美]约翰·杜威（2011）.民主主义与教育[M].王承绪.北京：人民教育出版社：153-162.

[4]陈鹏，黄荣怀，梁跃等（2018）.如何培养计算思维——基于2006—2016年研究文献及最新国际会议论文[J].现代远程教育研究，（1）：98-112.

[5]范文翔，张一春，李艺（2018）.国内外计算思维研究与发展综述[J].远程教育杂志，36（2）：3-17.

[6]傅骞，解博超，郑娅峰（2019）.基于图形化工具的编程教学促进初中生计算思维发展的实证研究[J].电化教育研究，40（4）：122-128.

[7]姜强，王利思，赵蔚等（2020）.认知水平与计算思维间的隐含关系挖掘——基于编程行为表征视角[J].现代远程教育研究，32（2）：94-103.

[8]姜乔（2019）.基于情境认知理论的地理教学情境设计[J].地理教学，（3）：33-36.

[9]兰国帅，郭倩，张怡等（2020）.影响未来高等教育教学的宏观趋势、技术实践和未来场景——《2020年EDUCAUSE地平线报告（教学版）》要点与思考[J].开放教育研究，26（2）：27-39.

[10]林琳，沈书生，李艺（2019）.谈设计思维发展高阶思维何以可能——基于皮亚杰发生认识论的视角[J].电化教育研究，40（8）：22-29.

[11]欧阳忠明，黄慧（2018）.工作场所作为学习环境：实现情境、实践与学习的联结——访国际知名工作场所学习专家史蒂芬·比利特教授[J].现代远程教育研究，30（5）：3-9.

[12]孙立会，王晓倩（2020）.计算思维培养阶段划分与教授策略探讨——基于皮亚杰认知发展阶段论[J].中国电化教育，（3）：32-41.

[13]田阳，万青青，陈鹏等（2020）.多空间融合视域下学习环境及学习情境探究[J].中国电化教育，（3）：123-130.

[14]王美，程佳铭，高守林（2018）.用技术赋能情境学习[J].现代教育技术，28（11）：12-18.

[15]王志军，刘潇（2019）.促进学习情境转化的增强现实学习资源设计研究[J].中国电化教育，（6）：114-122.

[16]吴忭，王戈（2019）.协作编程中的计算思维发展轨迹研究——基于量化民族志的分析方法[J].现代远程教育研究，（2）：76-84.

[17]张进宝（2019）.计算思维教育：概念演变与面临的挑战[J].现代远程教育研究，31（6）：89-101.

[18]张进宝，姬凌岩（2018）.中小学信息技术教育定位的嬗变[J].电化教育研究，39（5）：108-114.

[19]张沿沿，冯友梅，顾建军等（2020）.从知识结构与思维结构看思维评价——基于皮亚杰发生认识论知识观的演绎[J].电化教育研究，41（6）：33-38.

[20]赵国庆，熊雅雯，王晓玲（2018）.思维发展型课堂的概念、要素与设计[J].中国电化教育，（7）：7-15.

[21]鄭浩，王者鹤，马永红（2017）.OECD“催化剂项目”中的STEM教学模式及其启示[J].中国电化教育，（8）：53-59.

[22]郑瑶瑶（2014）.高中通用技术情境教学的实践研究[D].南京：南京师范大学：20-23.

[23]中华人民共和国教育部（2018）.普通高中信息技术课程标准[M].北京：人民教育出版社：6.

[24]ISTE & CSTA（2011）. Operational Definition of Computational Thinking for K-12 Education[EB/OL]. [2020-09-15].https：//id.iste.org/docs/ct-documents /computational-thinking-operational-definition-flyer.pdf.

[25]Selby， C. C.， & Woollard， J. （2013）. Computational Thinking： the Developing Definition[EB/OL]. [2020-09-18]. https：//eprints.soton.ac.uk/356481.pdf.

[26]Wing， J. M. （2006）. Computational Thinking[J]. Communications of the ACM， 49（3）：33-35.

收稿日期 2021-03-29责任编辑 杨锐

The Training Model of Computational Thinking  from the Perspective of

Learning Situation Chain Creation

YANG Wenzheng

Abstract： Thinking is situational， and the cultivation of thinking ability can only be realized with the help of specific situations. However， in the current teaching of computational thinking in primary and secondary schools， there are widespread deficiencies in situational creation， including obvious superficiality， weak coherence and insufficient ductility， etc.， which makes it difficult to effectively promote the sustainable development of students computational thinking ability. Creating a learning situation chain with multiple and interrelated situational elements can effectively avoid the phenomenon of “thinking jumping and interruption” in the development of students thinking， which is conducive to the formation of a learning situation loop that can promote the sustainable and progressive development of students computational thinking. Based on the perspective of learning situation chain creation， a training model of computational thinking is constructed. Through the creation of progressive problem situation， scaffolding inquiry situation， mutual assistance cooperation situation， equal communication situation and extensible application situation， this model forms a computational thinking training loop of “awakening， activation， strengthening and sublimation”， which helps to promote the spiral development of computational thinking. The application in the teaching practice of Scratch programming with the theme of “Recursive Algorithm—The Magical Fibonacci Sequence” shows that this model can better realize the cultivation of core computational thinking capabilities of students， such as problem definition， feature abstraction， algorithm design， evaluation iteration， migration application and so on.

Keywords： Computational Thinking; Training Model; Learning Situation Chain; Scratch Programming