高速铁路列车制动曲线速度分段方法

张友兵，陈志强，王建敏，张国振

（北京全路通信信号研究设计院集团有限公司 安全控制技术研究院, 北京 100070）

列车控制系统包括车载设备和地面设备，是保证高速铁路列车行车安全的核心系统。在列车运行过程中，车载设备根据行车许可、线路数据和列车制动参数计算目标距离连续速度控制模式曲线，对列车位置和速度进行实时监控，保证列车安全、高效运行［1-2］。

目前，我国高速铁路列车控制系统车载设备供应商主要采用欧标法和日立法2 种简化算法计算制动曲线。欧标法采用基于速度的减速度模型，将制动减速度分为6段，在每个速度分段内使用固定减速度，从行车许可终点迭代逆推计算制动曲线［3-6］。欧标法方法灵活，但是欧洲的ETCS 规范并没有给出具体可行的速度分段方法，且ETCS规范中的6段速度分段并不完全适合中国国内的所有列车类型。在日立法中，车载设备存储了7 档坡度下的制动距离表，将实际坡度信息归档到存储的坡度档位上，以便查找该坡度下的制动距离［7］。日立法将实际坡度归档到7档坡度，存在不可避免的归档误差，且通过查表计算列车制动距离的方法不够灵活。

在使用欧标法计算速度监控曲线时，对速度分段个数越多，速度分段内的固定制动减速度越接近列车真实的制动减速度，计算得到的速度监控曲线越精确。但是，速度分段个数越多，车载设备计算速度监控曲线需要执行的计算量越大，耗费时间越长，必然影响车载设备安全监控的实时性和及时性。因此，对列车速度进行合理分段，以较少的速度分段计算得到精确度足够高的速度监控曲线，就成为重要的研究内容。

本文针对欧标法计算列车制动曲线中的不足，提出基于减速度曲率进行速度分度与等间隔速度分段相结合的速度分段方法；以16编组的CRH 380AL高速动车组为例，根据其车辆制动参数进行速度分段并计算制动曲线，与采用基本速度分段计算得到的制动曲线进行比较，验证本文提出的速度分段方法的合理性和有效性。

1 减速度曲率分段与等间隔分段相结合的速度分段方法

1.1 基于速度分段的制动减速度模型

不同列车具有不同的制动性能，且在不同速度下具有不同的制动减速能力［8］。为了使用计算机计算列车的制动曲线，必然要对速度进行分段，1个速度分段内采用1个固定制动减速度。当前国际主流的采用目标距离连续速度控制模式的列控系统中，其制动减速度模型均采用基于速度的分段式减速度模型［9］。例如，按速度分段将车辆制动减速度分为6 档，如图1 所示。图中：v1—v6分别为速度分段点的速度，角标数字为对应的档位序号，后同；a1—a6分别为相邻速度分段点之间的恒定制动减速度；横线段表示速度分段内的恒定制动减速度。由图1 可知，在每个速度分段内的制动减速度为恒定值，这是根据速度分段点之间的基本速度分段制动减速度计算得到的（基本速度分段由车辆厂提供）。

图1 分为6段的制动减速度模型

1.2 基于速度分段的制动曲线计算原理

车辆提供的速度分段较细致，一般每5 km·h-1分为1 段；而列控车载设备计算制动曲线时，会从计算效率的角度以更大的速度步长进行分段，每个速度分段步长包括多个车辆提供的5 km·h-1基本分段制动减速度。假设制动减速度模型分为m个速度分段，每个速度分段包含n个基本速度分段，那么第i（i=1，2，…，m）个速度分段内的n个基本速度分段的制动减速度可分别表示为ai1，ai2，…，ain。对于第i个速度分段，可根据式（1）计算速度分段内车辆的平均制动减速度di，再根据式（2）计算对应的制动距离si［10-12］，最后根据式（3）对所有速度分段对应的制动距离求和，即可得到总的制动距离dbrake［13-14］。

式中：vi和vi+1分别为第i个速度分段的低速、高速分段点的速度，m·s-1。

基于图1 所示的6 段制动减速度模型，列车制动曲线的计算原理图如图2 所示。图中：d1—d7分别为以速度分段点的速度开始制动并停车，开始制动时的列车位置；vc为列车当前速度；点p7体现了列车的当前位置及对应的当前速度；点p1体现了列车制动停车后的位置及对应速度。由于点p1和点p2的速度已知、p1—p2间的制动减速度已知，那么可根据式（2）计算出从点p2制动到点p1所需要的制动距离。同理，还可根据式（2）依次计算出p3—p2，p4—p3，p5—p4，p6—p5和p7—p6所需要的制动距离；根据式（3）对所有制动距离求和，得到p7—p1的制动距离。

图2 基于速度分段的列车制动曲线计算原理

1.3 制动曲线计算

本文只研究速度分段对列车制动曲线的影响，因此不考虑坡度和轨道黏着系数对列车制动曲线的影响，也不考虑列车制动延时对列车制动曲线的影响。

设计列车制动曲线的计算流程及具体步骤如下。

第1 步：使用3 点求曲率方法计算所有基本速度分段点的减速度曲率，根据制动减速度的变化特点，将减速度曲率突变的点作为分段点，得到基于减速度曲率的速度分段。

第2 步：在高速阶段跨度较大的速度分段内进行等间隔速度分段，需要根据实际情况确定使用2等份或3 等份等间隔进行进一步的速度分段，得到最终的速度分段。其中，每个速度分段的2 端是2个不同速度的分段点，速度低的称为低速分段点，速度高的称为高速分段点。

第3 步：计算速度分段内所有基本速度分段的制动减速度的平均值，得到速度分段内的平均减速度或最小减速度，作为该速度分段的固定制动减速度。

第4 步：从速度为0 向制动初始速度逆推，计算相关速度分段的制动距离。不包含制动初始速度的速度分段，计算从高速分段点到低速分段点的制动距离；包含制动初始速度的速度分段，计算从制动初始速度到低速分段点的制动距离。

第5 步：对从制动初始速度到速度为0 范围内的所有速度分段的制动距离求和，得到列车从制动初始速度开始制动到列车停车所需要的列车制动距离。

2 基于减速度曲率的速度分段及验证

2.1 3点求曲率方法

在数学中，曲率（Curvature）是描述几何体弯曲程度的量，例如曲面偏离平面的程度，或者曲线偏离直线的程度。直线的曲率处处为零，圆上各点处的曲率等于半径的倒数，且半径越小曲率越大。

3 点求曲率方法的原理如图3 所示。图中：A点为二维坐标系oxy中的任意1 点，坐标为（x1，y1）；（x1，y1），（x2，y2）和（x3，y3）为不在1条直线上的任意3 个点坐标，根据平面几何基本定理，这3 个点必然能唯一确定1 个三角形，且这个三角形必然唯一存在1 个外接圆；a，b和c分别为唯一三角形的3 边边长；O为唯一圆（即曲率圆）的圆心；R为半径；斜线l为以A点为切点的圆切线。3点求曲率的具体方法为：利用式（4）—式（6）分别求出a，b和c；依据余弦定理，利用式（7）求出∠A的余弦；依据正弦定理，利用式（8）—式（9）求出∠A对边对应圆弧的曲率半径；曲率是曲率半径的倒数，即可求出点（x1，y1）的曲率［15］。

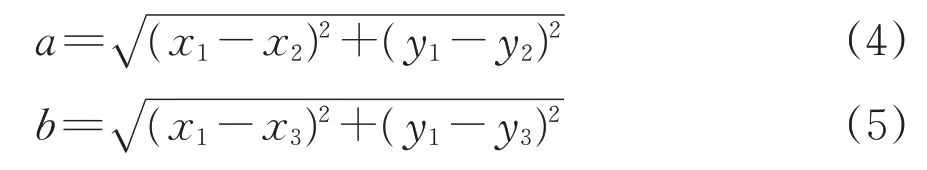
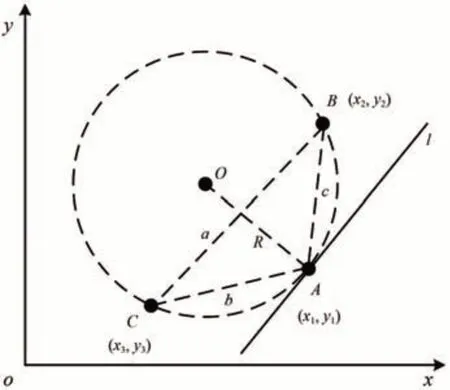
图3 3点求曲率方法原理

2.2 基于减速度曲率的速度分段

以CRH 380AL 型高速动车组为算例，采用其车辆制动参数作为试验数据。CRH 380AL 型高速动车组车辆提供的速度分段包含0～390 km·h-1共78 个等间隔的基本速度分段，每个基本速度分段的步长为5 km·h-1，速度分段内采用相同的制动减速度。每1 个等间隔的基本速度分段可被视为如图1 所示坐标系中的1 个坐标点，即速度坐标轴为横坐标，减速度坐标轴为纵坐标。除了第1 个点（速度取0 km·h-1时）和最后1 个点（速度取390 km·h-1时），其余76 个基本速度分段点的减速度曲率均可使用3点求曲率方法来计算。

比如，对于3个连续的基本速度分段点10，15和20 km·h-1，即2.78，4.17和5.56 m·s-1，对应减速度分别是1.121 7，1.239 0 和1.356 4 m·s-2，即这3个点的坐标分别为（2.78，1.121 7），（4.17，1.239 0）和（5.56，1.356 4）；利用3点求曲率方法，即可求出点（4.17，1.239 0）处的曲率为0.000 5，即15 km·h-1对应减速度的曲率为0.000 5。

同理，可以计算出所有76 个基本速度分段点的减速度曲率。不同速度下的列车制动减速度及对应的减速度曲率如图4 所示。由图4 可知：20，70，120和300 km·h-1这4个速度对应减速度的曲率明显偏大，说明列车制动减速度在这4 个速度点发生明显变化。根据这4 个列车制动减速度曲率突变点，将0～390 km·h-1速度曲线分为（0，20］，（20，70］，（70，120］，（120，300］ 和（300，390］共5个速度分段。减速度曲率较大的速度分段点及对应曲率见表1。

图4 不同速度下的列车制动减速度及曲率

2.3 制动曲线计算及验证

为了对比分析，采用前文方法，按表1 减速度曲率进行速度分段，计算得到列车制动距离；同时使用车辆厂提供的列车基本速度分段，再次计算列车制动停车的制动距离；计算2 种方法下制动距离的相对偏差，所有结果见表2。由表2 可知：当制动初始速度较小时，2 种方法求得的制动距离相对偏差很小，如列车制动初始速度分别为20，70 和120 km·h-1时，相对偏差均小于1 m；但当制动初始速度较大时，如制动初始速度为300 和350 km·h-1时，2 种方法求得的制动距离相对偏差均大于200 m，这是因为基于减速度曲率的速度分段跨度过大，速度分段内采用的固定减速度与实际减速度偏差较大，导致制动距离偏差较大，制动曲线计算精确度效果并不好。因此，为了提高制动初始速度较高时的列车制动距离的精确度，需要对基于减速度曲率的速度分段方法进行优化。

表1 减速度曲率较大的速度分段点

表2 5段速度分段下的制动距离计算

3 基于减速度曲率和等间隔的速度分段计算及验证

从式（2）可知，基于减速度曲率进行速度分段后，对于速度分段（120，300］和（300，390］，虽然速度分段内的基本速度分段点的减速度曲率很小，即制动减速度近似线性变化，但是速度分段跨度较大，速度分段内最小减速度和最大减速度差异较大，速度分段内的平均减速度已不能准确反映整个速度分段的减速度，所以计算出来的制动距离误差较大。因此，在基于减速度曲率的速度分段的基础上，需要在高速阶段的跨度较大的速度分段内再进行等间隔速度分段，比如2 等份或3 等份等间隔速度分段，降低速度分段内最小减速度和最大减速度的差异，使速度分段内的平均减速度更接近真实减速度。这样，虽然增加有限的速度分段个数，但可大大提高列车制动距离的计算精确度。

3.1 7段速度分段的制动曲线计算及验证

采用2 等份等间隔速度分段，即在（120，300］插入1个等间隔速度分段点210，在（300，390］插入1 个等间隔速度分段点345，将0～90 km·h-1分为（0，20］，（20，70］，（70，120］，（120，210］，（210，300］、（300，345］和（345，390］共7 个速度分段，基于减速度曲率分段和2 等分等间隔分段相结合的方法，得到的7 段速度分段下的制动减速度模型如图5 所示，图中a1—a7分别为相邻速度分段点之间的恒定制动减速度。基于该模型计算列车制动距离，并与基于基本速度分段计算得到的制动距离进行比较，结果见表3。由表3 可知，2 种方法求得的制动距离偏差大大降低，这说明在基于减速度曲率的速度分段的基础上，在高速阶段跨度较大的速度分段内再进行2 等份等间隔速度分段，可以提高制动初始速度较高的制动曲线的精确度。

图5 7段速度分段下的制动减速度模型

3.2 9段速度分段的制动曲线计算及验证

采用3 等份等间隔速度分段，即在（120，300］插入2 个等间隔速度分段点180 和240，在（300，390］插入2 个等间隔速度分段点330 和360，将0～390 km·h-1分为（0，20］，（20，70］，（70，120］，（120，180］，（180，240］，（240，300］，（300，330］，（330，360］和（360，390］共9 个速度分段，基于减速度曲率分段和3等分等间隔分段相结合的方法，得到的9段速度分段下的制动减速度模型如图6 所示，图中a1—a9分别为相邻速度分段点之间的恒定制动减速度。基于该模型计算列车制动距离，并与基于基本速度分段计算得到的制动距离进行比较，结果见表4。综合表3 和表4 可知：在速度分段内增加等间隔速度分段点，可以明显提高列车计算制动距离的精确度；并且增加的分段点数量越多，计算的列车制动距离的精确度越高。

表3 7段速度分段下的制动距离计算

图6 9段速度分段下的减速度模型

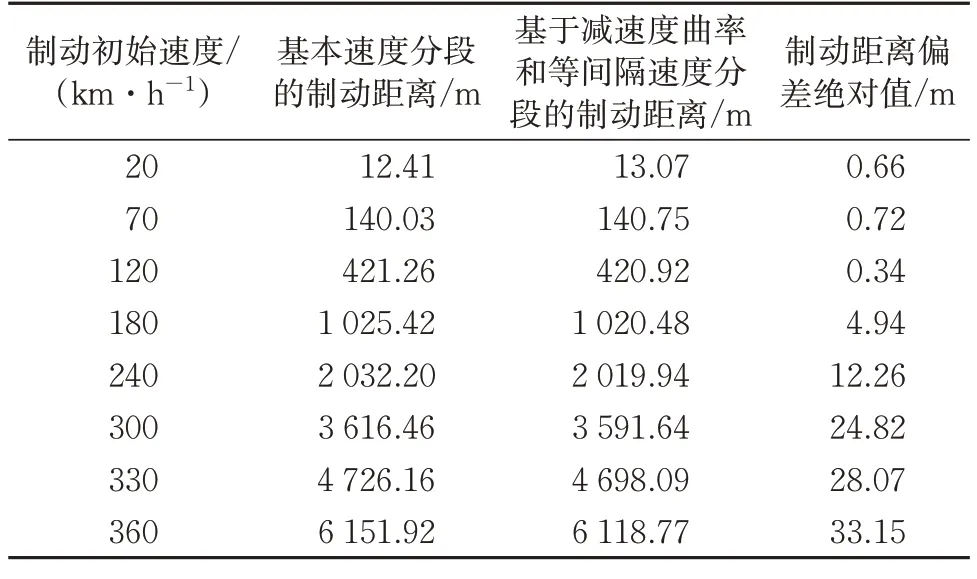
表4 9段速度分段下的制动距离计算

不同列车具有不同的制动性能，会计算得到不同的速度分段结果。如果要在其他型号列车上应用本方法，需要先根据减速度曲率进行1 次速度分段，再综合考虑制动曲线计算精确度和计算效率的要求，在1 次速度分段的基础上，通过等间隔分段进行2次速度分段，得到最终的速度分段。

4 结 语

在高速铁路列车控制系统中，车载设备实时计算速度距离监控曲线，并依据监控曲线对列车位置和速度进行安全防护，保证行车安全。由于不同速度下的列车制动减速度不同，需要对列车速度进行分段，速度分段内采用固定减速度，实现使用车载设备计算机计算制动曲线的目标。将速度分为多少段，如何分段，都会影响车载设备制动曲线计算结果的精确度和计算效率。本文提出了基于减速度曲率进行速度分度和等间隔速度分段相结合的速度分段方法，通过仿真试验，验证了本文提出的速度分段方法是准确且高效的，计算得到的列车制动曲线由于速度分段数量少，能够保证列车制动曲线的计算效率；由于速度分段合理，列车制动曲线计算结果精确度高，与使用基本速度分段得到的标准制动曲线偏差很小。因此本文提出的基于减速度曲率进行速度分度和等间隔速度分段相结合的速度分段方法在列车制动曲线计算结果精确度和计算效率间取得了良好的平衡，既能保证列车行车安全，又能提高列车运行效率。