重载列车紧急制动过程车轮踏面疲劳裂纹萌生寿命预测

董永刚，仪 帅，黄鑫磊，郑建校，杜晓钟，李树林

（1. 燕山大学 机械工程学院，河北 秦皇岛 066004；2. 西安建筑科技大学 机电工程学院，陕西 西安 710055；3. 太原科技大学 机械工程学院，山西 太原 030024；4. 太原重工轨道交通设备有限公司，山西 太原 030000）

铁路运输以其安全、快速、运载量大和运行成本低等优点，一直以来是最重要的货物运输方式。近年来随着我国经济高速发展，对煤炭、铁矿石、钢铁等货物的运输需求急剧增大，货运运力不足的问题越来越突出。货物列车高速重载化是解决货运列车运力不足的主要方式，也是当今铁路运输发展的主要方向。我国重载列车轴重已经逐步增大到25 t，30 t甚至40 t，某些货运列车运行速度已经从60 km·h-1逐步增大到120 km·h-1。随着列车向着高速化和重载化发展，制动时车轮踏面与闸瓦摩擦产生巨大的热量，闸瓦和车轮踏面表层温度急剧升高，随着热量的传导使车轮内部的温度达到一个极高的水平，这不仅导致车轮钢材料的硬度与强度发生改变，同时热应力也大幅增加。车轮旋转过程中车轮踏面除了承受闸瓦压应力、轮轨接触应力之外，还承受温度快速升高引起的热应力，在周期性机械载荷与热应力综合作用下，车轮踏面更容易发生热-机械疲劳损伤。

国内外学者从不同影响因素入手，对车轮踏面疲劳损伤进行研究。北京交通大学宋琳［1］利用铸钢车轮材料进行疲劳损伤试验，通过对裂纹断口微观形貌进行观察，发现不同的材质、载荷、环境介质、铸造缺陷等都会对裂纹形貌产生不同的影响。于荣泉［2］在有限元软件中建立轮轨滚动接触模型，通过仿真得到接触斑内应力场、应变场的分布，将应力、应变数据代入基于应变能和临界平面法的疲劳寿命预测模型中，并研究轮轨法向接触载荷以及摩擦系数对裂纹萌生寿命的影响。Esmaeili等［3］为了研究轮轨滚动接触条件下温度对车轮踏面裂纹萌生和扩展的影响规律，搭建了1∶1轮盘对转式制动试验台，结合有限元方法进行了模拟验证，最后还探讨了棘轮效应对疲劳寿命的影响。He 等［4］同样建立了轮轨滚动试验台，通过改变制动速度和制动力，研究摩擦产生的温度以及热应力对车轮型面损伤的影响，并且讨论了热疲劳裂纹的扩展行为，结果表明制动速度越高车轮表面的损伤划痕越明显，裂纹更倾向于朝车轮内部扩展，且车轮材料的屈服强度随着制动温度的升高而降低，更加剧了车轮的疲劳损伤。以往研究对车轮踏面裂纹萌生的研究大多都只考虑了外部机械载荷、车轮材质以及列车运行环境等影响因素，即使考虑温度效应对踏面损伤的影响，也没有延伸考虑热应力和热应变的影响。

本文着重研究踏面温度、热应力及热应变对疲劳裂纹萌生的影响。将列车制动工况、轮轨及闸瓦的材料性能、闸瓦-踏面接触条件、轮轨接触条件、热能交换条件等众多影响因素综合起来，采用Abaqus 有限元软件对重载列车紧急制动过程进行热力耦合仿真，求解车轮踏面温度场、应力场及应变场分布，并基于能量密度和临界平面法的多轴疲劳模型，得到踏面最大损伤参量的位置以及踏面温度、轴重、闸瓦压力与损伤参量之间的关系，对车轮踏面热-机械疲劳裂纹萌生寿命进行预测。

1 紧急制动过程热力耦合仿真

1.1 有限元模型建立

重载列车从制动开始到制动结束要行驶很长一段距离，在有限元软件中建立几百米长的轨道时计算资源过大，因此选用轨道轮替代真实的轨道进行建模。模型中，车轮直径为0.86 m、材料为CL60车轮钢、踏面为标准LM 磨耗型踏面；闸瓦为高磷铸铁闸瓦、宽度为0.05 m、弧长为车轮圆周长的1/5；轨道轮直径为1 m、材料为U71Mn 钢、轨道轮型面按照75 kg·m-1标准轨尺寸进行建模，在保证计算效率的前提下轨道轮半径尽可能大于车轮半径，以保证接触斑的形状和大小不受影响。采用Abaqus 有限元软件，建立闸瓦-轮对-轨道三维有限元模型如图1所示。

图1中，柱坐标系R，T和Z轴分别对应车轮的径向、切向（圆周方向）和轴向，将闸瓦力均匀施加在闸瓦钢背处，同时仅保留闸瓦沿车轮径向的自由度。将车轮中心O点与车轮轴孔进行耦合，轴重载荷施加在O点上，仅保留轨道轮绕轴线（Z轴）旋转的自由度，整体温度边界条件设为恒温26 ℃。选择动力-温度位移-显示分析步进行计算，车轮、闸瓦、轨道轮网格划分均为八结点热耦合六面体单元C3D8T，为了获取更为精准的仿真结果，在建模的时候除去不必要的倒角，并对车轮踏面接触区网格进行细化处理，如图2所示。

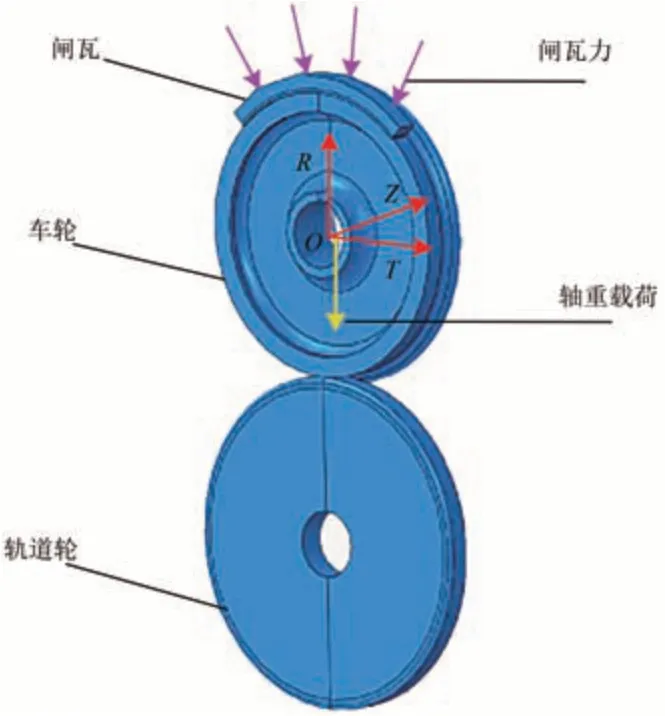
图1 闸瓦-车轮-轨道三维有限元模型

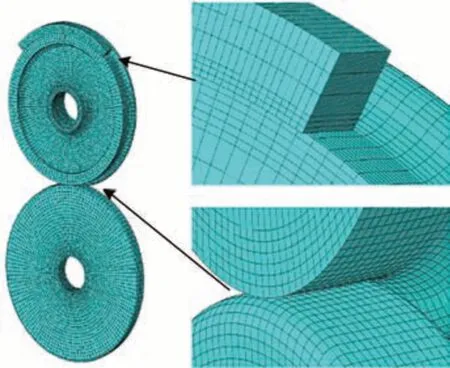
图2 闸瓦-车轮-轨道网格划分示意图

1.2 接触属性设置

在制动过程中，整个制动系统的热源输入除了包括踏面-闸瓦间摩擦产生的热量之外，还包括轮轨间微动滑移产生的热量，其中摩擦产生的热量绝大部分通过踏面传递到车轮内部，其余部分传递到闸瓦和轨道上或直接散失掉。传递到车轮内部的热能与摩擦总热能的比值称为热量分配系数，在Abaqus 软件中定义接触属性时将踏面-闸瓦、轮轨间的接触类型均设置为面-面接触，同时设定车轮的热量分配系数为0.90［5］。闸瓦-踏面间摩擦系数f1是与行驶速度、闸瓦压力相关的函数［6］，具体表达式如式（1）所示；轮轨间摩擦系数f2取定值0.3，均可在接触属性中进行设置。

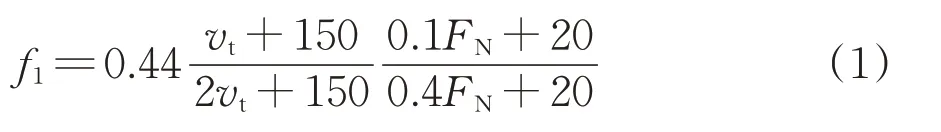
式中：FN为闸瓦压力，kN；vt为车轮运行速度，km·h-1。

对由闸瓦、车轮、轨道轮组成的整个系统而言，在确定了热源的输入方式和热量的分配比之后，还需要确定系统内部的热量传导以及与外部环境的热量交换。如果2个相互接触的物体或者1个物体内部不同位置存在温度差，就会有传热发生，踏面-闸瓦间与轮轨间的传热系数［7］均取109.43 W·m-2·K-1，材料内部的热量传导在定义材料属性之后由软件自行计算。物体辐射或吸收的能量与其表面积、表面黑度以及自身温度有关，Abaqus 软件中通过定义辐射率（即物体黑度）表征整个系统的辐射散热能力，闸瓦、车轮和轨道轮的系统辐射率根据经验取0.66［8］。摩擦产生热量的传递，除了以上2种传热方式之外还与周围空气存在对流换热，在计算对流换热散失的热量时，对流接触面积、流体温度都是初始条件，而壁面温度和车轮、闸瓦材料的热传导性能相关，也可以在Abaqus 软件中计算得到，因此只需要确定对流传热系数即可。对流换热系数αm的取值［9］依据经验公式，为

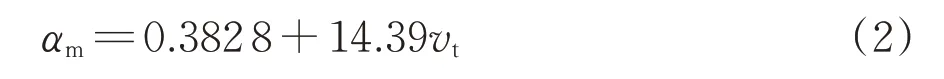
1.3 材料属性设置

重载列车在紧急制动过程中摩擦产生的高温，导致车轮钢和闸瓦材料的机械性能和物理特性发生改变，进而影响温度场和应力场的仿真结果。目前通过试验很难得到从常温（25 ℃）至600 ℃区间内CL60 车轮钢和高磷铸铁闸瓦的机械性能参数及物理性能参数，因此通过JMatPro软件［10］仿真获取；因密度和泊松比受温度影响较小，则均取定值。车轮钢材料的密度为7 850 kg·m-3，泊松比为0.3，闸瓦材料密度为6 740 kg·m-3，泊松比为0.28，其余受温度影响变化较大的参数取值分别见表1和表2。在仿真中轨道轮始终保持恒温，因此不需考虑高温对其材料参数的影响。轨道轮材料密度为7 830 kg·m-3，泊松比为0.29，抗拉强度为883 Mpa，比热容为1.57 J·kg-1·K-1，线膨胀系数为3.28×10-3K，传热系数为0.17 W·m-1·K-1，切变模量为79.2 GPa，弹性模量为210 GPa，屈服强度为620 MPa。

热塑性状态下材料的应力应变关系尚不明确，为了对热弹塑性问题进行分析，选用双线性等向强化准则对其描述［11］。任意温度下车轮、闸瓦和轨道轮材料的本构方程可用弹塑性曲线表示，如图3所示。图中：σ和ε分别表示材料的应力和应变；E为弹性模量；σs为屈服强度；Ep为强化模量。

图3 中，屈服阶段之后的曲线斜率为强化模量，其与弹性模量的关系为

式中：ζ为材料泊松比。

表1 CL60车轮钢材料参数

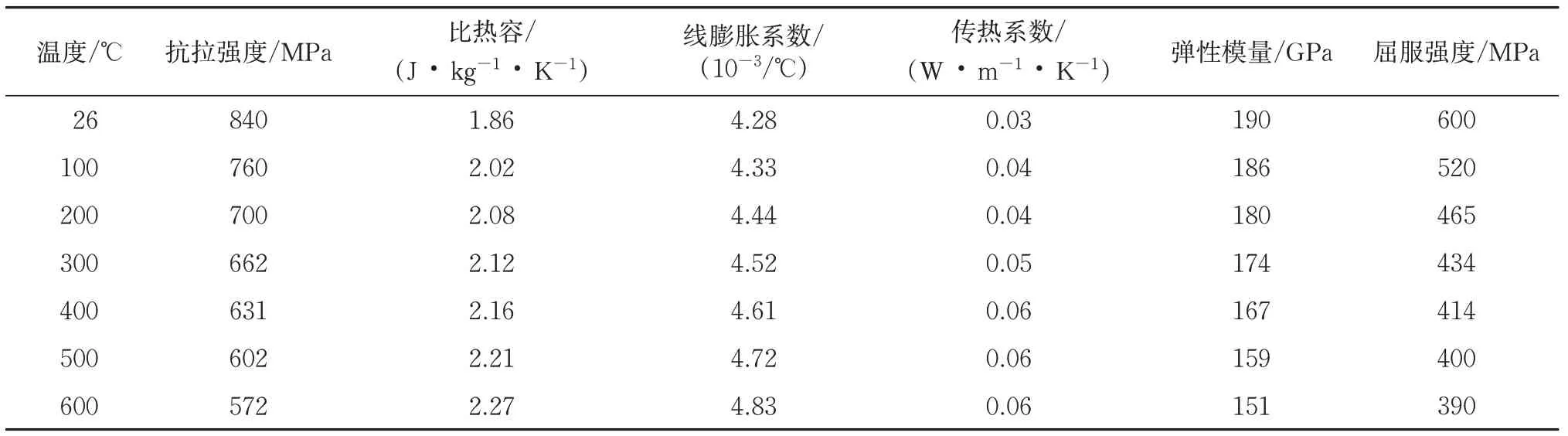
表2 高磷铸铁闸瓦材料参数

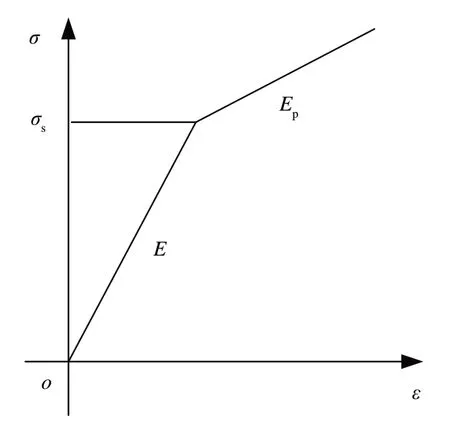
图3 某温度下弹塑性曲线

2 疲劳裂纹萌生寿命预测模型

对于车轮踏面热-机械疲劳裂纹萌生寿命预测，采用Jiang 和Sehitoglu 提出的基于能量密度和临界平面法的多轴疲劳模型［12］，踏面表层材料的疲劳裂纹萌生寿命取决于裂纹萌生面上法向应力、应变以及切向应力、应变分量的大小，损伤参量FP为

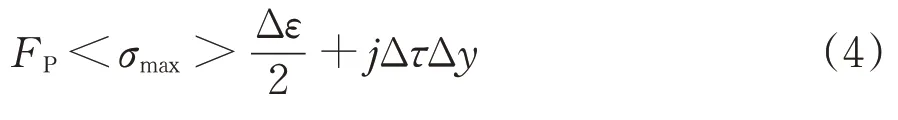
其中，

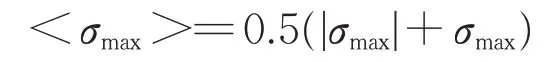
式中：＜＞为MacCauley 括号；σmax为裂纹萌生面上最大正应力；Δε为裂纹面上正应变范围；Δτ为裂纹面上剪切应力范围；Δγ为裂纹面上剪切应变范围；j为与材料和载荷相关的常数（可由拉伸/扭转试验测得）。

FP的最大值用FPmax表示，FPmax所在的平面即为裂纹萌生面，FPmax与疲劳裂纹萌生寿命Nf之间的关系式［13］为

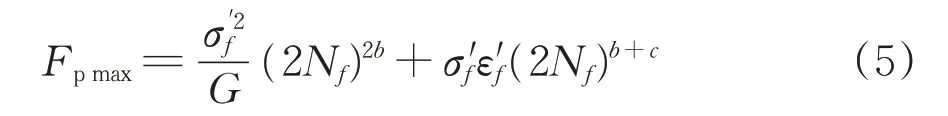
式中：σ′f和ε′f分别为疲劳强度系数和疲劳延性系数；b和c分别为疲劳强度指数和疲劳延性指数。

式（5）中的参数取值参考文献［14］并结合四点关联法对不同温度下的参数进行估值，结果见表3。

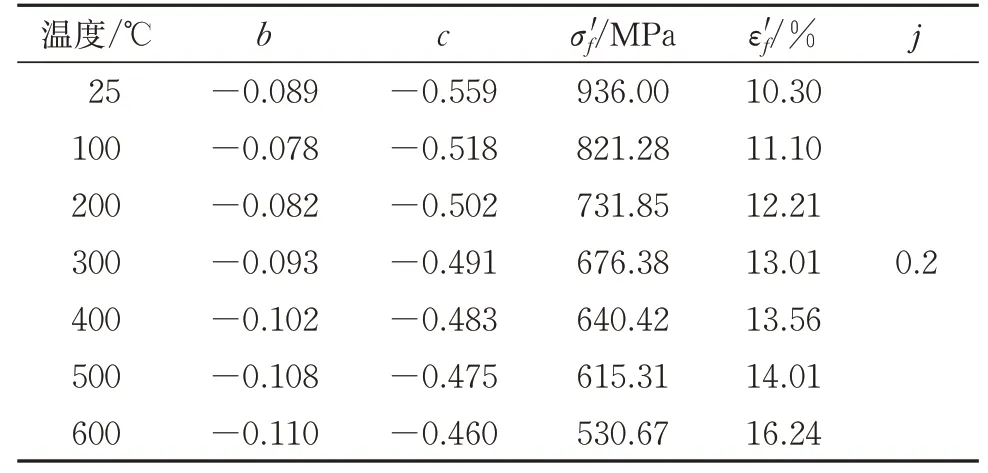
表3 车轮钢寿命预测模型材料参数

3 结果分析

3.1 车轮踏面温度分布

在动力学软件中以轴重30 t、初速度100 km·h-1、环境温度25 ℃、闸瓦压力21 kN对重载列车实际制动工况进行仿真，得到制动速度曲线如图4所示。

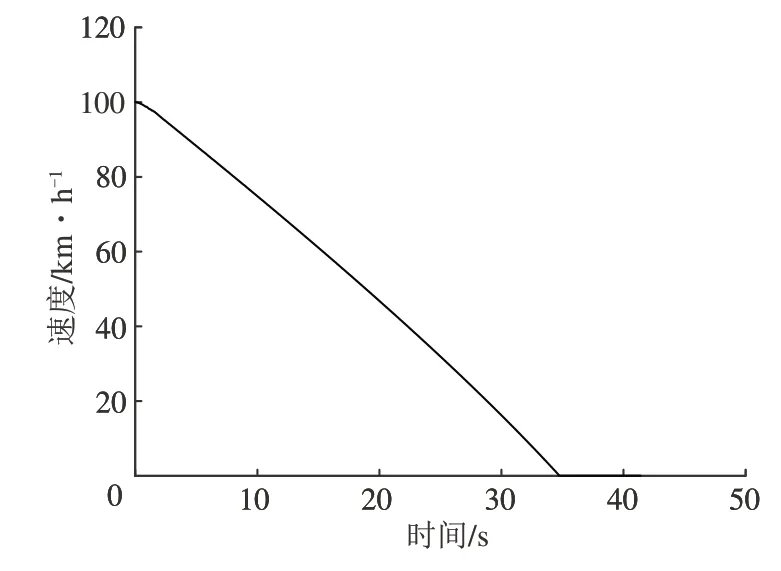
图4 制动速度曲线

制动总时间为35 s、制动距离为513 m、车轮旋转圈数为190 圈，将闸瓦压力和制动速度曲线导入有限元软件中进行制动分析。制动结束后，在车轮踏面上沿轴向（正向为车轮外侧指向轮缘侧）选择1 排固定节点集A，将所有节点上的温度提取出来。在轴向上踏面中间区域温度上升速度最快，且温度也高于2 侧区域，最高可达到567 ℃，车轮踏面温度分布云图如图5所示。

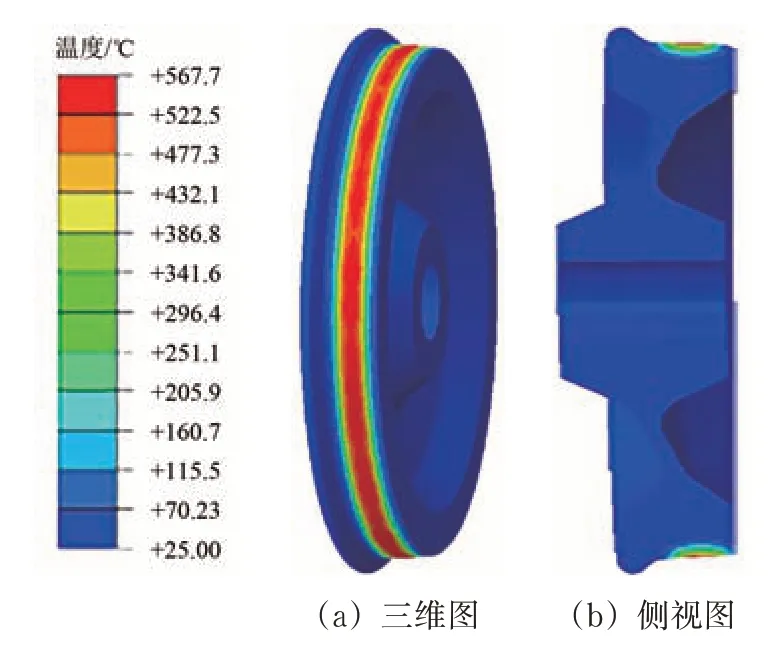
图5 踏面温度最高时刻分布云图

制动前期（0～10 s）由于车轮旋转速度较快，踏面与闸瓦摩擦剧烈，因此温度上升迅速；在制动中期（10～20 s）由于速度的下降，温度上升速度逐渐趋于平缓，在第15 s时车轮踏面温度达到制动全程的峰值；制动后期（20～35 s）由于速度下降，此时摩擦产生的热量小于散射的热量，踏面温度逐渐回落。将节点集A上的温度数据通过Matlab软件绘图，得到完整制动过程踏面温度分布如图6所示。

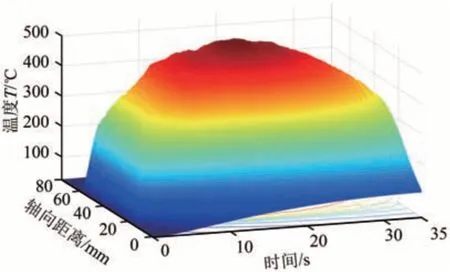
图6 踏面温度随时间变化趋势

制动温度最高时刻车轮踏面上的应力分布云图如图7 所示。图中：径向应力指向车轮外侧为正值，切向应力与车轮旋转方向一致为正值。从图7可见：接触斑内轮轨接触应力远大于踏面热应力，所以接触斑区域始终处于受压状态，最大径向压应力为332.7 Mpa；切向应力受制动力（即闸瓦摩擦力）与热应力的影响较大，是多种残余应力在切向方向不断累积的结果，最大切向压应力为710.7 MPa。

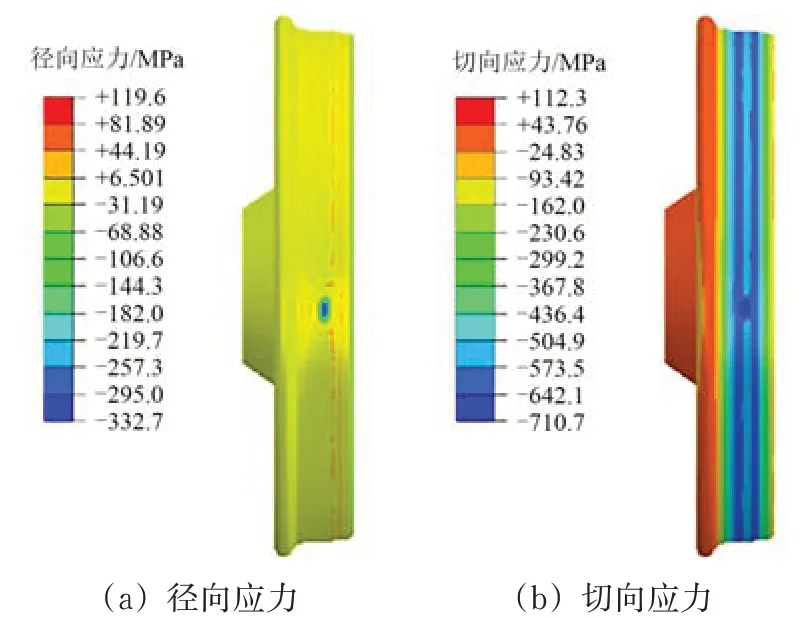
图7 踏面应力分布云图

沿轴向将节点集A内所有节点的径向应力、切向应力依次输出，通过Matlab 软件绘制三维图分别如图8 所示。从图8 可见：在接触斑之外的区域，其应力变化幅度很小，接触斑内径向最大拉应力为5.1 MPa，最大压应力为510 Mpa；制动前期车轮与闸瓦摩擦剧烈，导致车轮踏面温度上升较快，热应力与闸瓦摩擦力的残余应力导致切向应力上升幅度明显，切向应力在第14 s 时达到峰值，为-640 MPa，后期随着温度回落应力有所下降。

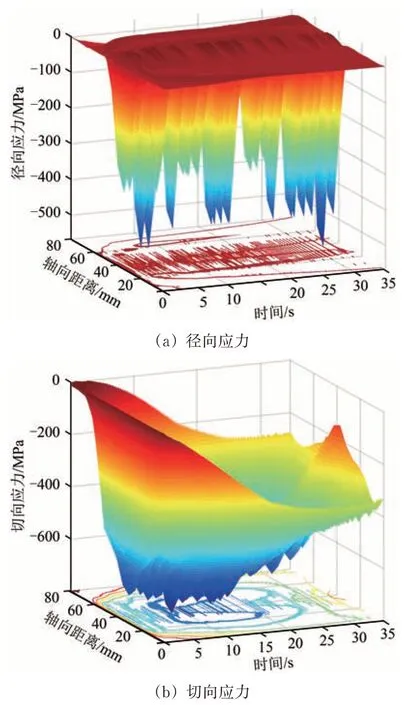
图8 车轮踏面应力随时间变化趋势

为了分析温度对踏面应力分布的影响，得到不同温度时应力沿轴向分布如图9所示。从图9可见：随着温度的升高，接触斑内径向应力有减小的趋势，在100 ℃时接触斑内最大径向应力为372 MPa，当温度上升到567 ℃时减小为190 Mpa，造成这种现象有2 个原因：一是因为受温度影响，车轮材料强度有所下降，导致接触斑面积变大，所以接触斑内最大径向应力降低；二是受热应力的影响，接触斑应力与热应力相互抵消掉一部分；随温度升高，踏面切向应力有所增大，这是由于在制动前中期闸瓦-踏面间摩擦残余应力不断累积以及热应力共同导致的，在100 ℃时踏面最大切身应力为215 MPa，当温度升高到567 ℃时为640 MPa。

图9 不同踏面温度时应力沿轴向分布

3.2 车轮踏面应变分布

根据式（4）可知，材料的应变及其方向也是影响裂纹萌生的重要因素。仿真得到车轮踏面径向应变随时间变化趋势如图10 所示。从图10 可见：踏面材料沿径向方向上的弹性应变主要是因热应力造成的，最大值为1.81×10-3，随着时间推移温度和热应力逐渐下降，弹性变形逐渐恢复；在制动第9 s时，当热应力超过材料的屈服极限开始出现塑性应变，最大值为2.10×10-3，随后虽然温度和热应力逐渐下降，但是材料产生的塑性变形已不会恢复。

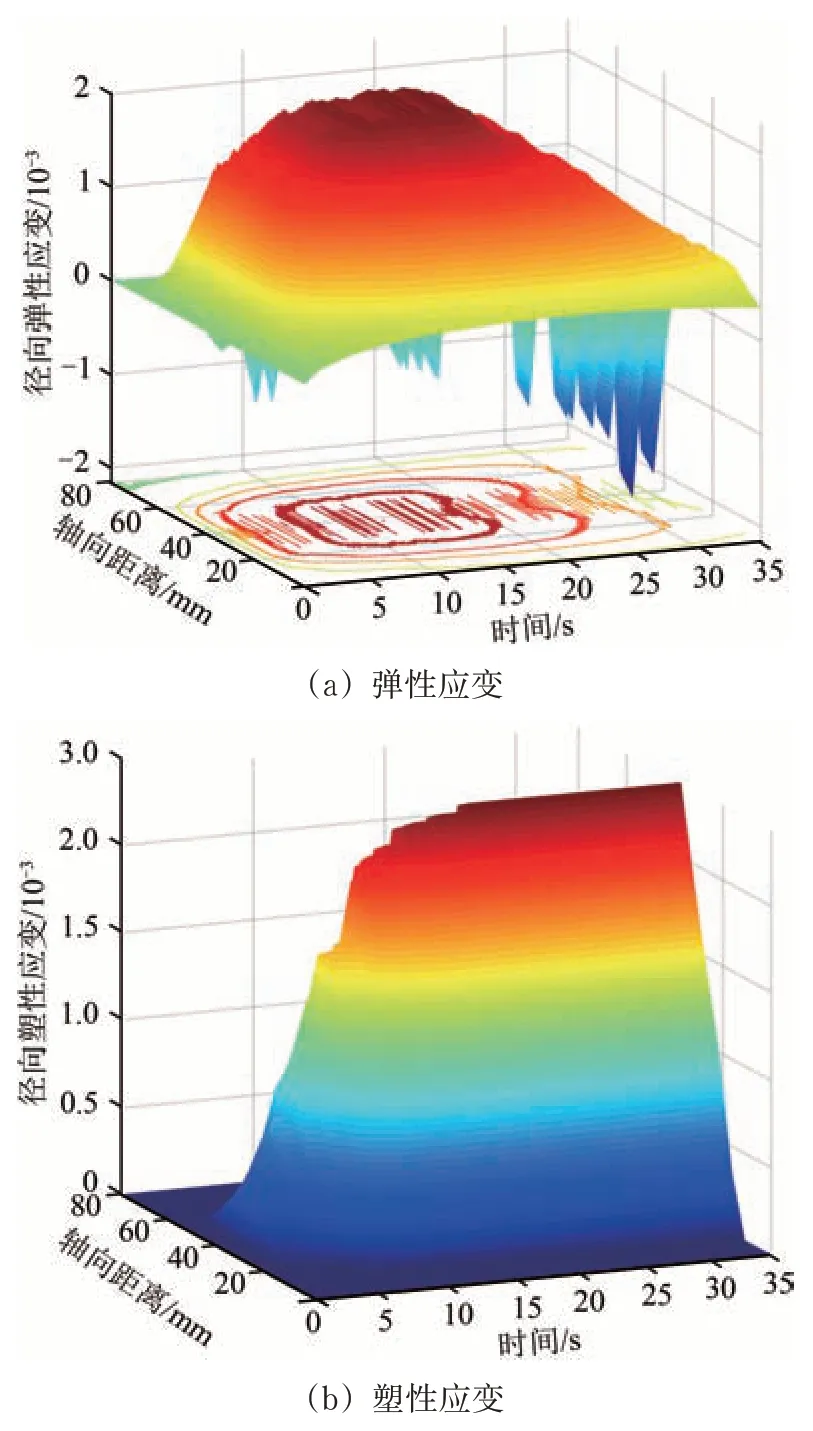
图10 车轮踏面径向应变随时间变化趋势

仿真得到车轮踏面切向应变随时间变化趋势如图11 所示。从图11 可见：踏面材料沿切向方向的弹性应变，主要是由切向应力引起的变形，其整体分布趋势与切向应力的分布趋势极为类似，切向应变的峰值为-4.0×10-3；在制动第14 s 时切向塑性应变达到峰值-1.8×10-3。

图11 车轮踏面切向应变随时间变化趋势

3.3 疲劳裂纹萌生寿命预测

由于节点集A包含了车轮踏面整个横截面上的节点，可通过计算节点上的损伤参量判断踏面上的裂纹萌生位置。在接触斑区域内材料始终处于受压状态，这样不利于裂纹的萌生，裂纹萌生面上最大正应力σmax始终为负值，因此FP=jΔτΔγ，但接触斑内的切向应力和切向应变相对大于踏面其他区域，因此需要将接触斑与其他区域的损伤参量进行比较，最终确定最先损伤位置。

在制动过程中车轮踏面不同位置承受的应力和应变有较大差异，通过数据分析计算之后得到不同制动温度下各节点的损伤参量沿轴向分布如图12 所示。从图12可见：在闸瓦摩擦区内损伤参量都处于较高水平，但损伤参量最大值始终位于接触斑区域内。

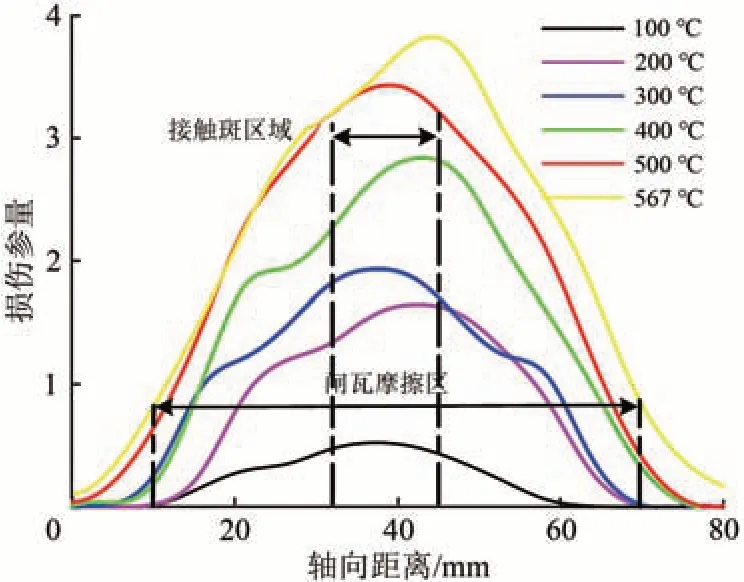
图12 各节点损伤参量沿轴向分布

损伤参量最大值FPmax所在的节点均在轴向距离32～45 mm 区间内，FPmax与制动温度之间基本呈线性关系，当温度达到最高567 ℃时，相对应损伤参量最大值FPmax＝3.801 1，具体如图13所示。

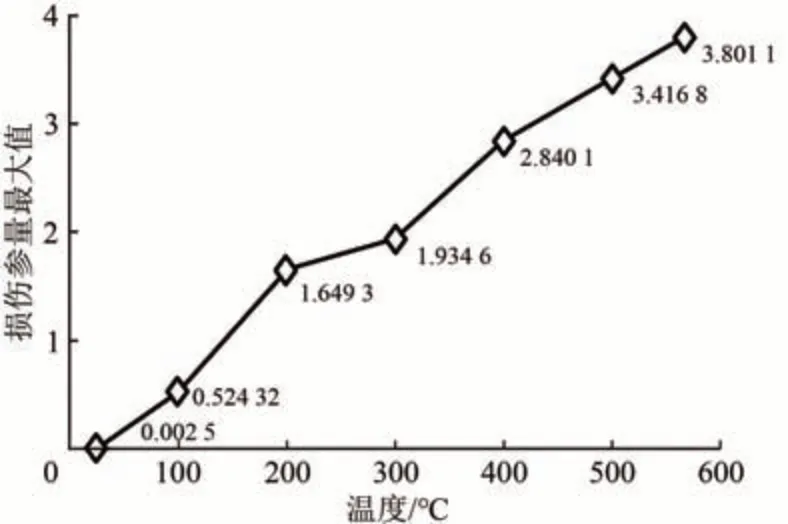
图13 不同温度下踏面材料损伤参量最大值

通过剪切型疲劳寿命预测公式即式（5），得到FPmax与疲劳寿命（循环次数）间的关系如图14 所示。从图14 可见：在不同的温度下都有相对应的寿命曲线。

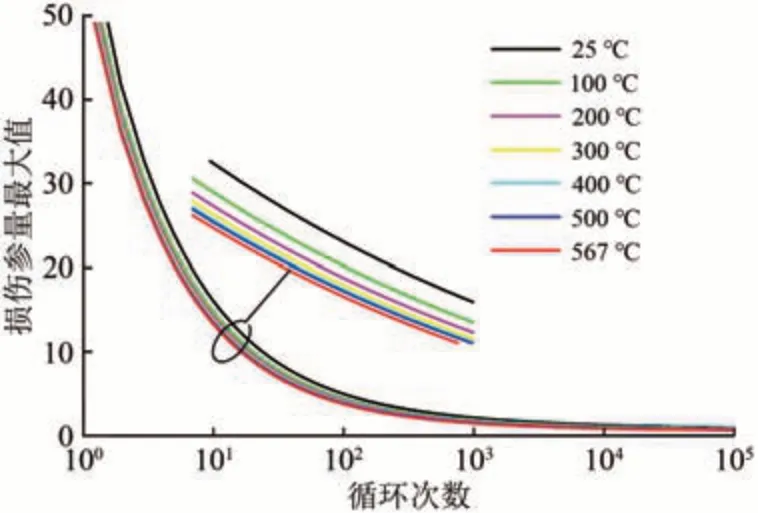
图14 不同温度下车轮材料疲劳寿命曲线

通过图14且根据FPmax查找相对应的循环次数，当FPmax=3.801 1 时车轮材料疲劳寿命Nf=236 次，表示在所分析的制动工况下可以进行236 次往复制动。

为了更全面地分析不同制动工况对车轮材料疲劳寿命的影响，保持初速度100 km·h-1恒定，改变轴重分别为20，23，25 和27 t，且轴重为27 t时闸瓦压力分别为17，19和24 kN，分析不同制动参数对损伤参量以及疲劳裂纹萌生寿命的影响规律，结果见表4。

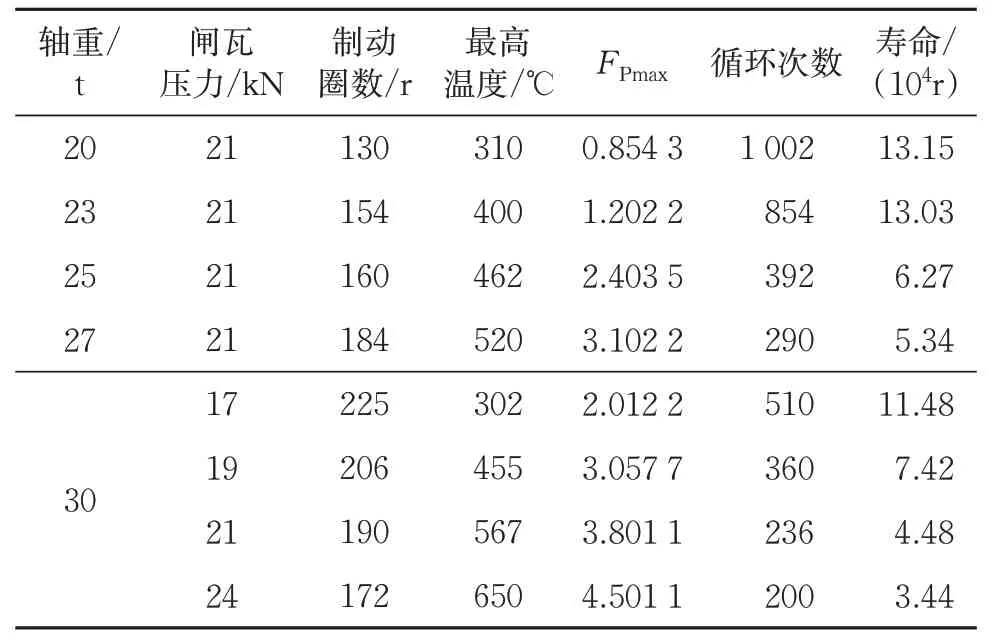
表4 制动参数对疲劳裂纹萌生寿命的影响

轴重的大小代表着动能的转化量，闸瓦压力的大小代表动能的转化效率，表3是对单一变量进行分析的结果。从表4可见：闸瓦压力保持不变（21 kN），当轴重小于23 t时，制动产生的踏面最高温度水平较低，这种工况下对裂纹的萌生寿命影响较小；当轴重继续增大，最高温度值上升明显，致使裂纹的萌生寿命大幅度降低；轴重保持不变（30 t），此类工况已经属于载重较大的范畴，最高温度值与闸瓦压力的关系更加敏感，因此为了避免产生严重的裂纹损伤，闸瓦压力应该控制在1 个较小的范围内，从寿命突变较大的点来看，闸瓦压力应不大于17 kN或者将踏面温度控制在300 ℃以下。

4 结 论

（1）车轮踏面温度变化对热-机械疲劳损伤影响较为严重，尤其当温度大于100 ℃时，踏面上应力、应变增大较为明显，损伤参量FPmax与温度基本呈线性增长趋势，致使踏面疲劳寿命大幅缩短，踏面温度最高时损伤参量达到最大值；低于100 ℃时材料的力学性能受温度影响有所缓和，损伤参量值随温度线性增长趋势放缓。

（2）车轮踏面上接触斑承受较高的交变应力，始终处于受压状态，其裂纹萌生面上的正应力为0，但由于其切向应力、应变大于踏面其他区域，因此FPmax仍处于接触斑内的节点上，并且车轮踏面裂纹萌生受剪应力和剪应变的影响比较大。

（3）当轴重为30 t、闸瓦压力为21 kN、初速度为100 km·h-1进行紧急制动时，损伤参量最大为3.801 1，在此制动工况下最大循环制动次数仅有236 次。接触斑内最大压应力达到510 MPa，而脱离接触斑区域后径向拉应力最大值仅为5.1 MPa，整个踏面上切向应力分布并没有有大差异，最大切向应力出现在温度最高的时刻，约为640 MPa。