气动荷载作用下高速铁路隧道衬砌结构的疲劳累积损伤及残余寿命计算方法

杜建明，高修强，房 倩，麦海颖，王 赶，海 路

（1. 北京交通大学 土木建筑工程学院，北京 100044；2. 北京交通大学 隧道及地下工程教育部工程研究中心，北京 100044；3. 中国电力建设集团有限公司 华东勘测设计研究院有限公司，浙江 杭州 310014）

1964年日本东海道新干线高速铁路系统成功运营后［1］，高速列车通过隧道诱发的气动效应对列车与隧道的负面影响逐渐凸显。高速列车车头进入隧道诱发压缩波，车尾进入隧道诱发膨胀波，压缩波与膨胀波不断产生并往复传播，以音速在隧道内壁、列车外壁、隧道进出口等位置间持续反射、连续叠加及激发，形成复杂波系［2-4］。在作用于隧道壁面的空气压力（压缩波产生的压力和膨胀波产生的拉力，即气动荷载［5］）循环作用下，隧道衬砌结构的原生裂纹会持续发展并相互贯通，从而降低衬砌结构完整性与耐久性，甚至诱发铁路隧道衬砌脱落、掉块等安全事故。例如1999年11 月28日，日本礼文滨铁路隧道因衬砌脱落、掉块导致列车脱轨，造成后续51 班次列车行程被迫取消、8 500名乘客滞留车站的严重后果。事后分析认为：铁路列车在隧道内所产生的气动荷载长期循环作用可能是事故发生的重要诱因之一［6］。为了防止我国高速铁路隧道运营过程中发生类似的安全事故，开展衬砌结构在气动荷载长期循环作用下的疲劳累积损伤发展规律研究，对隧道内高速列车的安全营运具有重要的现实意义。

目前，关于高速列车通过隧道诱发气动效应的研究中，对高速列车的研究主要集中在车体密封性、车内乘客舒适性以及车体疲劳强度特性等研究方面，对高速铁路隧道的研究主要集中在隧道内部结构安全性、隧道内压力波变化规律及分布特征、隧道洞口微气压波、隧道内双车交会以及特殊环境下气动效应等研究方面。已有大量国内外专家学者对上述问题的影响因素进行了系统的分析研究，并取得丰硕的研究成果，如列车速度、隧道长度、车内位置等因素对列车车体气密性及车内乘客舒适性的影响［7-9］；列车单车通过隧道及双车在隧道内交会时气动荷载对车体疲劳强度的影响［10］；隧道拱顶衬砌背后存在空洞时，不同车速下气动荷载对衬砌结构受力特性的影响［11］；列车速度、列车编组形式、隧道长度、车隧阻塞比等因素对隧道内压力波变化及分布特性的影响［12-15］；隧道洞口缓冲结构形式、隧道内通风竖井及辅助坑道、碎石道床等对隧道洞口微气压波的缓解［16-18］；列车速度、列车编组形式、列车鼻尖长度、隧道长度、隧道内交会位置、车隧阻塞比等因素对隧道内双车交会时压力波气动荷载分布特性以及列车空气阻力系数的影响［19-21］；海拔高度、温度等环境因素对高速铁路隧道气动效应力学特性的影响［22］等等。然而，目前尚鲜见针对高速铁路隧道衬砌结构疲劳累积损伤及残余寿命分析的研究成果。

本文基于高速铁路隧道壁面气动荷载特征，综合Miner 损伤理论与混凝土应力-疲劳寿命曲线（S-N曲线）的特点，考虑气动荷载间相互作用以及列车通过隧道不同次数间的影响，提出1 种气动载荷作用下的高速铁路隧道衬砌结构疲劳累积损伤与残余寿命分析方法；结合京沪高铁德州—枣庄段某隧道工程，研究高速列车单次通过隧道后气动荷载持续周期数以及列车车速对衬砌结构疲劳损伤的影响，分析列车通过隧道次数与衬砌结构疲劳累积损伤及残余寿命之间的关系，判断隧道设计年限内气动荷载长期循环作用下的衬砌结构安全性。

1 高速铁路隧道壁面气动荷载特征

高速列车单次通过隧道时，隧道壁面纵轴中断面上作用的气动荷载时程曲线可简化为图1 所示。图中：以横坐标为零表示列车车头驶入隧道入口的时刻；T为高速列车车尾驶出隧道出口后气动荷载峰值的衰减周期。将整个气动荷载时程曲线划分为列车在隧道内行驶和列车完全驶出隧道2 个阶段，由图1 可知，当列车在隧道内行驶时，由于列车的存在，隧道壁面气动荷载峰值变化无严格规律可循；而当完全驶出隧道（自车尾刚好离开隧道出口时起）后，隧道壁面气动荷载峰值变化近似呈周期性衰减规律，且正负峰值近似相等。结合现场实测结果分析可知［23］，列车完全驶出隧道后，隧道壁面气动荷载峰值的衰减周期T可表示为

图1 高速铁路隧道壁面气动荷载时程曲线简化示意图

式中：L为隧道长度；c为当地声速。

影响T衰减速率的因素主要有隧道长度与壁面粗糙程度等。一般而言，隧道壁面气动荷载最大值既可能发生在列车在隧道内行驶阶段，也可能发生在列车完全驶出隧道阶段，且列车完全驶出隧道阶段的气动荷载持续时长是列车行驶于隧道内时长的9.0倍［24］。在常温无腐蚀环境下，载荷停歇对大多数材料的疲劳强度影响不大［25］，故在研究气动荷载对衬砌结构疲劳累积损伤过程中，可忽略2 列高速列车通过隧道时间间隔的影响。

高速铁路隧道设计年限一般为100年。以京沪高速铁路沪宁段为例，线上日开行高速列车209对，当某高速列车以时速300 km 的速度通过长度1 005 m 的隧道时，根据现场实测结果［26］可知，隧道壁面气动荷载持续周期数达30 次，则沿线隧道衬砌结构所受气动荷载次数为4.6×108次。相比混凝土拉压屈服强度，气动荷载峰值极小（1.5～5.0 kPa），但气动荷载会影响衬砌结构内部缺陷发展规律，从而使得衬砌结构内部细观裂纹最终发展为宏观裂缝。

2 衬砌结构疲劳累积损伤及残余寿命算法推导

2.1 疲劳累积损伤过程

假设初始状态损伤为零，在等幅循环荷载作用下，Miner 理论与实际情况下的疲劳累积损伤过程如图2 所示。图中：u为等幅循环荷载作用次数，为便于分析，暂取u=5；黑线表示单次循环荷载作用下疲劳损伤；红线表示循环荷载相互作用对疲劳累积损伤过程的影响量。由图2（a）可知，工程实际中高周等幅疲劳循环荷载相互作用会加剧疲劳累积损伤过程，增大疲劳累积损伤，降低残余寿命，且循环荷载之间的疲劳累积损伤相对增量会随循环次数的增加而逐渐增大，表现为显著的非线性。由图2（b）可知，由于没有考虑荷载相互作用对疲劳累积损伤过程的影响，通过Miner 损伤理论得到的循环荷载作用下的结构疲劳累积损伤及残余寿命分析，会产生较大的结果偏差，因此尚需进一步提高计算精度。

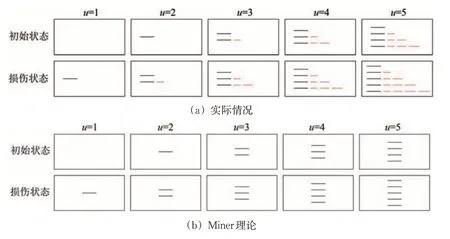
图2 等幅循环荷载作用下疲劳累积损伤过程简化示意图（假设初始状态损伤为零）

2.2 疲劳损伤及残余寿命计算步骤

引入相邻荷载间相互作用因子描述气动荷载间的相互作用，在定义完整衬砌结构受列车单次通过隧道后引起的疲劳损伤，并推导得到其计算式之后，基于损伤相对增量，衡量列车多次通过隧道引起的累积损伤，提出1种高速列车多次通过隧道后的衬砌结构疲劳累积损伤及残余寿命分析方法，具体步骤如下。

步骤1：计算列车单次通过隧道引起的衬砌结构疲劳损伤。

根据线性损伤准则以及荷载相互作用因子，定义衬砌结构在列车单次通过隧道后引起的疲劳损伤Di为

其中，

式中：ni为高速列车第i次通过隧道时气动荷载周期数；j为高速列车第i次通过隧道时气动荷载的第j个周期；dij为高速列车第i次通过隧道时第j个周期的气动荷载作用下衬砌结构产生的损伤，量纲为1；αij为相邻气动荷载间的相互作用因子；Pij为高速列车第i次通过隧道时第j个周期下的气动荷载峰值，αi1=1。

因研究对象为完整无缺陷的衬砌结构，假设初始损伤为0。

步骤2：计算列车多次通过隧道引起的衬砌结构累积损伤。

根据线性损伤准则以及损伤相对增量，定义衬砌结构在列车多次通过隧道后引起的累积损伤Dsum为

其中，

式中：m为高速列车通过隧道的次数；Δβi为高速列车第i次通过隧道时产生的衬砌结构疲劳损伤相对增量。

由于等幅循环荷载之间疲劳累积损伤相对增量差异较小，可近似认为等幅循环荷载相互作用之间的疲劳累积损伤增量相等，即Δβi为不变常数。在参考相关文献［27-28］对等幅循环荷载相互作用参数定义及取值的基础上，定义Δβi的取值范围为（0.1～1.0）/m。

步骤3：计算衬砌结构残余寿命。

衬砌结构残余寿命可根据衬砌结构损伤临界值与列车多次通过隧道引起的累积损伤分析得出。参考既有研究成果［29-30］，视衬砌结构损伤临界值Dcr为归一化后量纲为1的参数，即

此时衬砌结构残余寿命Dre为

2.3 列车通过隧道次数对衬砌结构残余寿命的影响

若以列车通过隧道次数与隧道寿命期内计划通过次数之比为列车通过隧道相对次数γm，则Dre与γm之间的关系如图3所示。由图可知：在列车通过隧道次数一定时，残余寿命随列车通过隧道产生的损伤相对增量β的增加而逐渐减小；当相对增量β一定时，残余寿命Dre随列车通过隧道次数的增加而逐渐减小；在相同受力条件下，相比Miner（α=0）公式，考虑荷载间相互作用以及列车通过隧道不同次数间的影响后，疲劳累积损伤增加，残余寿命减小，计算结果符合工程实际情况。

图3 结构残余寿命与列车通过隧道相对次数之间的关系

3 工程应用

3.1 工程概况

京沪高速铁路德州—枣庄段某隧道长1 005 m，断面面积100 m2，曲率半径7 000 m，坡度3‰；隧道内部铺设无砟轨道，轨间距5.0 m。试验中通过隧道的高速列车为8 辆编组的CRH 型动车组，车体全长201.4 m，鼻尖长度9.55 m，车身断面面积11.20 m2［26］。高速列车通过隧道的次数取实际京沪高铁的日开行对数209对。

由于洞口设有缓冲措施，隧道洞口壁面气动荷载峰值相对较小，故选择隧道纵轴中部壁面为研究对象。在靠近车体1 侧、距轨面高1.5 m 处的隧道壁面粘贴多个动态压力传感器，获取高速列车经过隧道时隧道壁面承受的气动荷载［26］；在求得高速列车单次通过隧道引起的衬砌结构疲劳损伤的基础上，进而计算得到列车多次通过隧道后的衬砌结构疲劳累积损伤及残余寿命。

3.2 列车单次通过隧道时气动荷载持续周期数对衬砌结构疲劳损伤的影响

1）计算参数

当列车以300 km·h-1的速度通过隧道后，距隧道入口500 m、距轨面高1.5 m 处隧道壁面测点的气动荷载时程曲线如图4 所示［26］。当高速列车在隧道内部行驶时，由于车体本身的存在，气动荷载峰值呈现不规则变化。为便于分析，对高速列车在隧道内行驶阶段的气动荷载进行修正，用该阶段最大峰值代替其余峰值，即曲线中的红色部分。由图4 可知：当高速列车全部驶出隧道后，气动荷载呈现周期性衰减规律，此时的气动荷载正、负峰值可近似认为相等，在后续分析中取二者中的较大值作为气动载荷峰值。

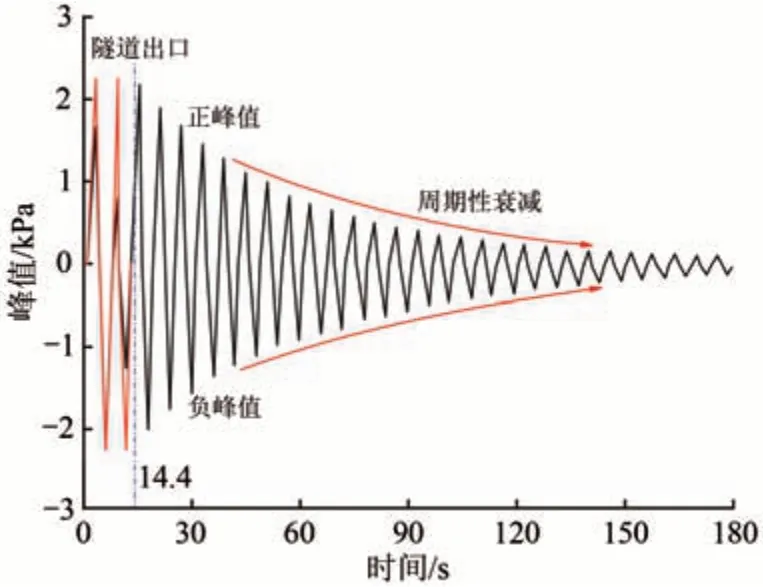
图4 距隧道入口500 m、距轨面高1.5 m 处隧道壁面测点气动荷载时程曲线

根据文献［31］，混凝土材料的极限循环次数N与循环拉、压应力之间的关系式可表示为

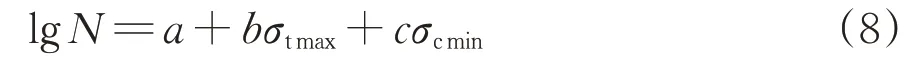
式中：a，b和c为材料参数，通过拟合曲线可求解；σcmax和σtmin分别为压应力最大值和拉应力最小值。

在等幅循环荷载作用下，拉、压应力相等，式（8）可简化为

式中：d为材料参数；P为等幅循环荷载峰值。

根据气动荷载时程曲线可以得到气动荷载周期数以及峰值参数；根据式（3）可以利用荷载峰值参数求解相应的荷载之间相互作用因子α1j（此处只研究列车单次通过隧道的情况，故i=1）；再利用材料S-N曲线，可以求解得到对应的极限循环次数N1j。计算结果见表1。

2）拟合结果

高速列车单次通过隧道时，衬砌结构疲劳损伤与气动荷载持续周期数之间的关系及拟合曲线如图5所示，得到的拟合函数见式（10），此时R2=0.999 9。

由图5 和式（10）可知：衬砌结构疲劳损伤Di随气动荷载持续周期j的增加而逐渐增大，且二者之间存在明显的线性关系；高速列车单次通过隧道对衬砌结构诱发的疲劳损伤为25.60×10-12。结合表1 进一步得知，参数α1j的变化范围为［0.83，1.00］，平均值0.90，与直线斜率接近。

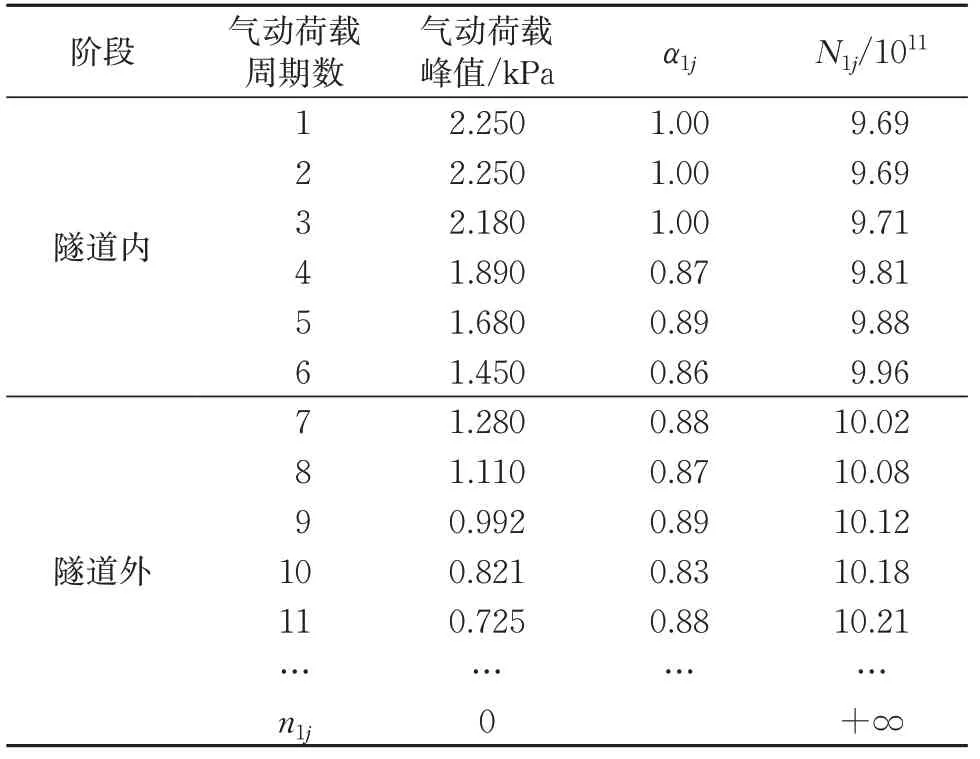
表1 计算参数（部分）

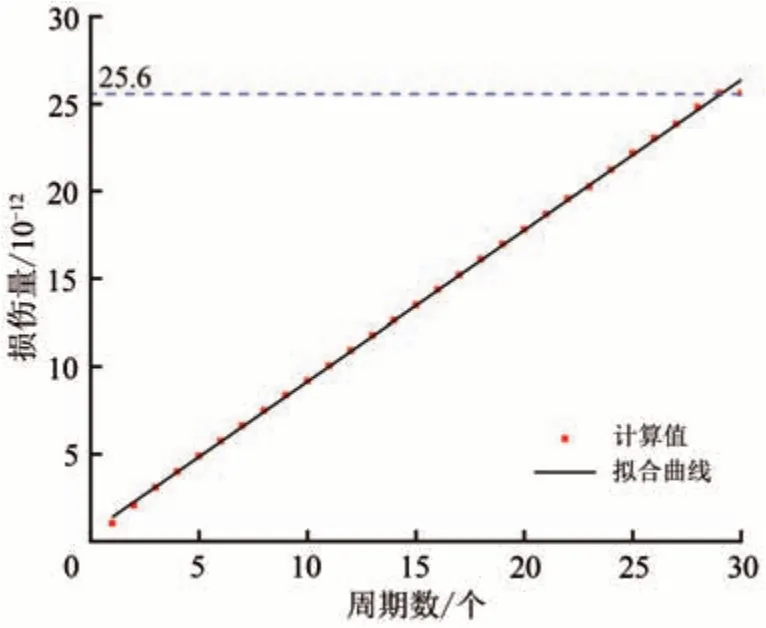
图5 疲劳损伤与荷载持续周期数之间的关系

3.3 列车单次通过隧道时车速对衬砌结构疲劳损伤的影响

以距隧道入口400 m、距轨面高1.5 m 处的隧道壁面为研究对象，结合现场实测数据［26］，分析不同车速下，高速列车单次通过隧道时的车速对衬砌结构疲劳累积损伤的影响规律。

1）不同车速下气动荷载的变化规律

不同车速下，高速列车单次通过隧道时在隧道内行驶和完全驶出隧道这2 个阶段下的气动荷载峰值与车速之间的关系，以及相应拟合函数、可决系数如图6 所示［26］。由图可知：高速列车在隧道内行驶阶段诱发的气动荷载峰值均大于驶出隧道阶段；高速列车在隧道内行驶阶段，气动荷载峰值P内随列车速度v的提高而逐渐增大，二者之间的关系可近似用二次函数表示；高速列车驶出隧道阶段，气动荷载峰值P外随列车速度v的提高先增加后减小，二者之间的关系可用三次函数表示。

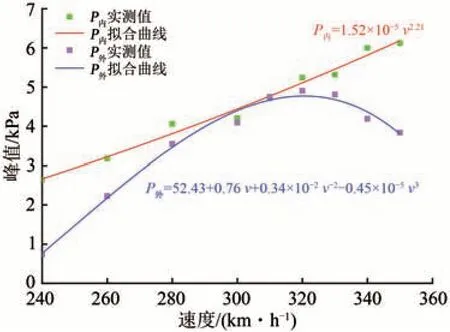
图6 气动荷载峰值与列车速度之间的关系

2）不同车速下气动荷载持续周期数对疲劳累积损伤的影响

不同车速下，高速列车单次通过隧道时的衬砌结构疲劳损伤与气动荷载持续周期数之间的关系如图7所示。由图可知，衬砌结构疲劳损伤Di随气动荷载持续周期数j的增加而逐渐增大，且二者之间存在明显的线性关系。据此得到的拟合函数及可决系数整理见表2。

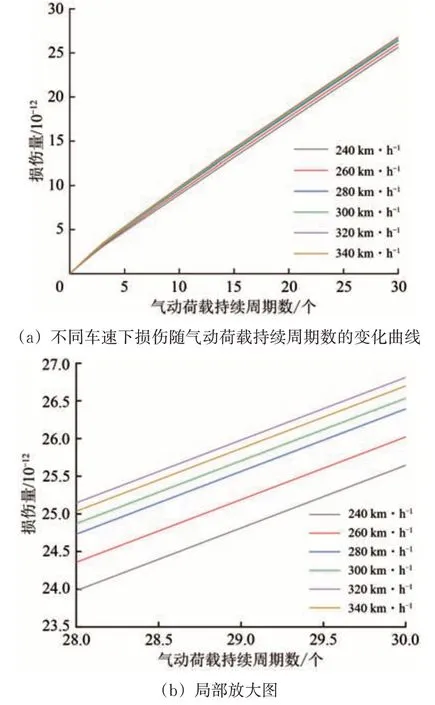
图7 不同车速下衬砌结构疲劳损伤与气动荷载持续周期数之间的关系

由表2 可知：不同车速下，高速列车单次通过隧道时影响隧道壁面气动荷载峰值衰减的因素相同，即不同车速下的衬砌结构疲劳损伤与气动荷载持续周期数之间的线性关系相似；隧道内列车不断诱发、反射、叠加的压缩波与膨胀波传播与反射机制极其复杂，导致不同车速下的气动载荷峰值存在差异，不同车速下衬砌结构疲劳损伤与气动荷载持续周期数之间的线性斜率即q值也存在微小差异。

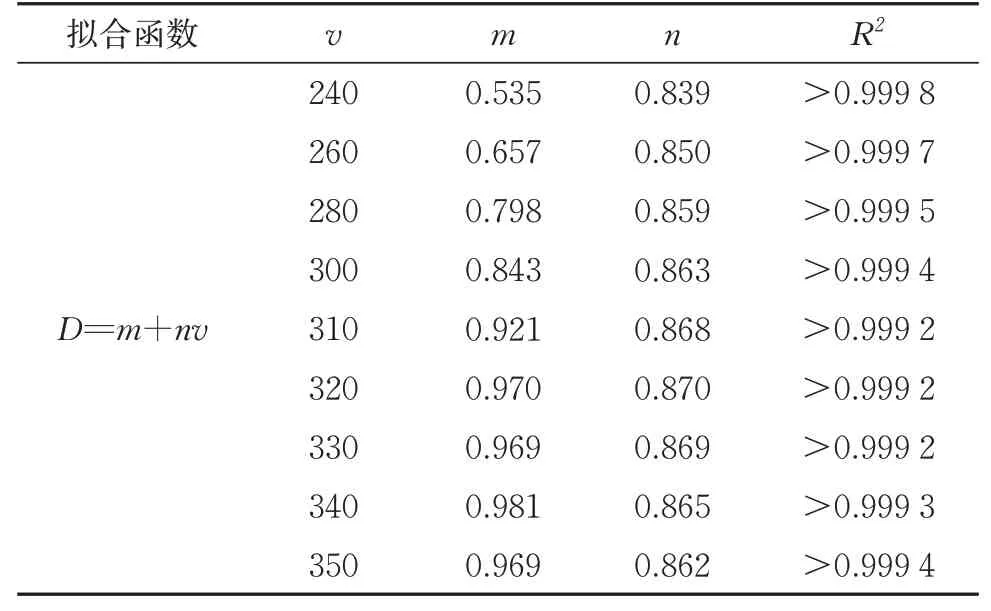
表2 不同车速下衬砌结构疲劳损伤与气动荷载持续周期数之间的拟合函数

3）列车速度对衬砌结构疲劳损伤累积的影响

高速列车单次通过隧道时，衬砌结构疲劳累积损伤Di与列车速度v之间的关系如图8 所示。由图可知：衬砌结构疲劳损伤随着列车车速的提高先增加后减小，二者间的变化规律与高速列车驶出隧道阶段的气动荷载峰值与速度之间的变化规律相似。

图8 衬砌结构疲劳损伤与列车速度之间的关系

3.4 列车多次通过隧道后衬砌结构疲劳累积损伤与残余寿命

以距隧道入口500 m、距轨面高1.5 m 处隧道壁面为研究对象，列车时速300 km，在高速铁路隧道设计年限内，衬砌结构疲劳累积损伤、衬砌结构残余寿命以及列车通过隧道次数（周期数）之间的关系如图9所示。

图9 衬砌结构疲劳累积损伤、衬砌结构残余寿命与列车通过隧道次数之间的关系

由图9 可知：衬砌结构累积损伤随周期数的增加而逐渐增大，残余寿命则逐渐减小，疲劳累积损伤与残余寿命之间存在明显的负相关关系；当周期数达到0.95（α=0.1/N）和0.81（α=0.5/N）时，疲劳累积损伤已达临界损伤值，说明循环荷载之间的相互作用对疲劳累积损伤具有加速效应，在一定程度上增加了结构疲劳累积损伤，降低了结构残余寿命；在相同的受力条件下，相比于Miner 公式（α=0），在考虑循环荷载之间的相互作用以及对疲劳累积损伤作用的影响后，结构疲劳累积损伤增加、残余寿命减小，且增加量或减小量均随循环荷载对疲劳累积损伤影响程度的增大而逐渐增加。

3.5 隧道设计年限内的衬砌结构疲劳累积损伤

根据前文计算可知，对于京沪高速铁路德州—枣庄段某隧道，时速300 km 高速列车单次通过隧道诱发的衬砌结构疲劳损伤为25.6×10-12。在日开行高速列车209 对的相同工况下，每天因高速列车通过隧道诱发的衬砌结构疲劳累积损伤为10.7×10-9，每年为3.9×10-6，100年（该隧道设计年限内）为3.9×10-4，远远小于衬砌结构损伤临界值1。这说明高速列车经过隧道诱发的气动荷载对完整衬砌结构的疲劳累积损伤影响可以忽略不计，研究成果与既有工程经验相符。

4 结 论

（1）基于高速铁路隧道壁面气动荷载特征，综合考虑气动荷载相互作用以及列车通过隧道不同次数间的影响，提出1 种高速铁路隧道完整衬砌结构疲劳累积损伤及其残余寿命分析方法，依托京沪高铁德州—枣庄段某隧道工程的计算结果表明，该分析方法符合工程实际情况。

（2）高速列车单次通过案例隧道对衬砌结构诱发的疲劳损伤为25.6×10-12；衬砌结构疲劳损伤与气动荷载持续周期数之间存在明显的线性关系，这种关系与高速列车驶出隧道后气动荷载峰值的衰减规律密切相关；衬砌结构疲劳损伤随车速的提高先增加后减小。

（3）高速列车多次通过案例隧道后，衬砌结构疲劳累积损伤随列车通过隧道次数的增加逐渐增大，残余寿命则逐渐减小。在日开行高速列车209对的相同工况条件下，每天因高铁列车通过隧道诱发的衬砌结构疲劳累积损伤为10.7×10-9，每年为3.9×10-6，100年（隧道设计年限内）为3.9×10-4，表明气动荷载长期循环作用下，完整的衬砌结构在案例隧道设计年限内不会发生损伤破坏。

（4）考虑到高速铁路隧道衬砌结构疲劳累积损伤过程不仅受到高速列车诱发的气动效应影响，将来可考虑气动荷载对衬砌结构裂缝扩展的加速效应，进一步从缺陷衬砌结构角度开展疲劳累积损伤及残余寿命影响方面的相关研究。