特大跨钢管混凝土拱桥徐变效应分析
2021-10-19李勇岐孙旭东李学钦薛晓芳
曾 勇,李勇岐,孙旭东,李学钦,薛晓芳,
顾安邦1,2,谭红梅1,2
(1. 重庆交通大学 山区桥梁及隧道工程国家重点实验室,重庆 400074;2. 重庆交通大学 山区桥梁结构与材料教育部工程研究中心,重庆 400074)
因跨度大、结构轻、经济性好、造型美、施工便捷、节省材料等突出优点,钢管混凝土拱桥在我国得到了较多建造[1],目前我国的钢管混凝土拱桥已接近500 多座。与普通钢筋混凝土不同,钢管混凝土的管内混凝土具有处于3向受压状态、养生时不浇水、混凝土与外界隔绝、与外界没有湿度交换等特点[1]。大跨钢管混凝土拱桥在施工过程中存在多次体系转换,属于高次超静定结构,且由于拱桥拱肋弦管内混凝土是逐步浇筑形成的,因此弦管内混凝土之间存在龄期差别。
李生勇等人[2]基于龄期调整有效模量法与混凝土弹性徐变理论,分析了某钢管混凝土铁路拱桥徐变效应。武文杰等人[3]基于混凝土徐变的B3 模型[4],采用按龄期调整有效模量法,考虑几何非线性和施工过程的徐变效应,分析了某大跨度中承式钢管混凝土拱桥的徐变效应。蒋伟等人[5]把修正龄期有效模量法和有限单元法进行结合,讨论了持荷水平、长细比、矢跨比、截面含钢率和混凝土加载龄期等因素对钢管混凝土拱试验模型的因徐变引起的横向稳定承载力的影响。曹国辉等人[6]对8 根钢管混凝土试件进行了870 d 的室内环境徐变测试,基于混凝土徐变的继效流动理论和多轴徐变理论[7-8],提出了钢管混凝土徐变系数预测模型。彭建新等人[9]引入混凝土换算弹性模量,通过变形协调条件推导了钢管混凝土拱肋应力重分布计算公式,并进行了钢管混凝土拱桥节段模型的徐变试验验证。
已有的研究表明,徐变对大跨度钢管混凝土拱桥的拱肋跨中挠度增量、拱肋钢管应力增加和混凝土应力减小具有不同程度的影响,对钢管混凝土拱桥的线形、内力与结构安全造成较大的影响,徐变效应显著。尽管目前对钢管混凝土的徐变进行了试验与理论研究,得出许多重要的结论[10-14],但钢管混凝土的徐变影响因素多,徐变效应仍需要进一步研究。目前,钢管混凝土拱桥的数量较多,但对特大跨钢管混凝土拱桥的徐变系数、应力重分布特点及实桥徐变应力实测研究仍然较少,可供参考的钢管混凝土拱桥徐变试验与现场实测数据依然有限。因此,进一步开展特大跨度钢管混凝土拱桥徐变效应研究具有重要理论意义与工程价值。
单纯采用有限元方法或理论分析手段很难全面分析特大跨钢管混凝土拱桥的徐变效应,而结合钢管混凝土构件模型徐变试验和实桥应力监测是研究钢管混凝土拱桥徐变规律的重要手段。
本文结合某特大跨钢管混凝土拱桥,采用试验、有限元模拟和实桥应力监测相结合的方法,研究特大跨钢管混凝土拱桥的徐变效应。
1 实桥概况
某特大跨钢管混凝土拱桥的主孔净跨460 m,吊杆和立柱间距为12.0 m,如图1 所示。大桥有2 个钢管混凝土桁架拱肋,拱肋间中距为19.7 m,单肢拱肋宽4.14 m。拱顶截面高7.0 m,拱脚截面高14.0 m。每条拱肋由4根Φ1 220 mm×22 mm 钢管、内灌C60混凝土的钢管混凝土弦杆组成,钢管混凝土桁架由4根弦杆通过Φ711 mm×16 mm横联钢管和Φ610 mm×12 mm 竖向钢管连接而成。桥面以上的拱肋设“K”形横撑,桥面以下的拱脚段拱肋设“米”形撑,横撑均为空钢管桁架。

图1 某特大跨钢管混凝土拱桥
大桥的施工顺序:CS1工序为钢管骨架按吊装顺序施工,拱肋合拢,形成无铰拱,各扣索保留5%左右的索力;CS2—CS9 工序分别为灌注与养护1#—8#主弦管内混凝土,并相应地调整索力,灌注顺序如图2 所示;CS10 工序为拆除扣索与临时构件,安装立柱和吊杆;CS11 工序为分别安装桥面系的横梁与纵梁;CS12工序为铺设桥面铺装、栏杆等二期恒载;CS13工序为730 d(2 a)时收缩徐变完成;CS14 工序为1 000 d(3 a)时的收缩徐变完成。
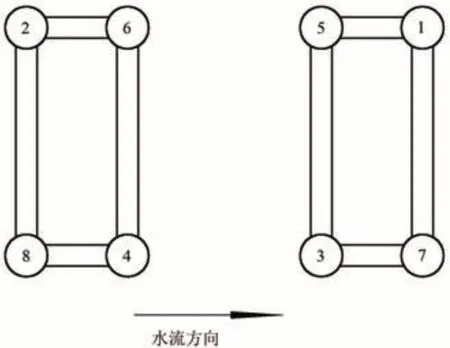
图2 管内混凝土的灌注顺序
在全桥拱肋的0L, 1/8L, 1/4L, 3/8L,1/2L,5/8L,3/4L,7/8L和L(L为该桥的净跨径)等控制截面处,分别安装应变计,分别测量管内混凝土与钢管的应力,其中,0L截面处于南岸拱脚,L截面处于北岸拱脚,4/8L为拱顶处。在每个控制截面处,混凝土内有3 个埋入式应变计(测量结果取其均值),钢管外表面的4个象限点装有表贴式应变计。
2 钢管混凝土构件徐变模型试验
2.1 模型试验
钢管混凝土构件的徐变试验往往受试验设备和场地条件的限制,试验构件的直径都较小,试验结果能否全面反映特大跨度钢管混凝土拱桥的大直径弦杆的钢管混凝土收缩徐变效应需要进一步研究。本节以上述实桥的拱脚段主弦杆为背景[7,11],开展大直径钢管混凝土构件徐变效应试验研究,通过模型试验观测钢管混凝土收缩徐变引起的内力重分布现象,以期从试验的角度研究徐变效应。
本模型的几何缩尺比为1∶2.5,加载吨位结合实桥拱脚段弦管的实际受力和试验室的加载设备情况,按180 t进行模型试验加载。
具体的试验包括2 个部分:①利用补偿模型进行钢管混凝土构件收缩与温度效应试验;②利用加载模型进行轴心受压下大直径钢管混凝土构件的徐变效应试验。
混凝土配合比与材料来自于实桥。补偿模型和加载模型的钢管混凝土构件的钢管截面尺寸均为Φ450 mm×20 mm,内灌C60混凝土。补偿模型和加载模型的数量各有1个,均放置于试验室的同一位置,可以视为是处于相同的温度与湿度环境。补偿模型不进行加载,通过比较补偿模型与加载模型之间的应变差值,剔除2 个模型的温度应变和收缩应变,从而分离出同一环境下的加载模型的徐变应变。
在管内混凝土养护龄期达到14 d后,通过反力架上的4 个千斤顶给加载模型施加总计180 t 的轴心荷载,每个千斤顶平均施加45 t的力。各千斤顶后安装有压力式传感器,定期监测加载吨位和微调千斤顶的压力,以使千斤顶的总加载力值保持在180 t。模型在试验初期有明显的收缩徐变效应,需要每天测量应变并及时微调4个千斤顶的加载力值,后期收缩徐变效应趋于平稳。为补偿加载模型因徐变效应可能导致的模型长度变化,在反力架后面安装若干个弹簧,从而保证外加荷载不变。模型试验如图3所示。

图3 大桥拱脚段主弦管节段模型试验
在2 个试验模型的跨中钢管外表面的4 个圆周4 分点处安装表贴应变计,跨中截面的混凝土内部埋设3 个内埋式应变计,定期分别测量钢管与混凝土的应力,每次测量时均记录当时的温度和湿度等环境参数。由于收缩徐变效应的影响,2 个模型在试验开始时应变增长较大,需每天进行应变测量,90 d 后每2 d 进行1 次应变测量,试验半年后每周进行1次应变测量。整个试验时间为期1 a。
为了对比钢管混凝土构件模型的收缩徐变,在恒温恒湿的环境条件下还分别进行了7,14,28 和90 d 4 个加载龄期的C60 素混凝土收缩徐变试验。C60混凝土的材料和配合比与钢管混凝土构件的管内混凝土为同一批次材料,混凝土性能一致。
2.2 试验结果
14 d加载龄期的加载模型的钢管混凝土的徐变应变、徐变系数和补偿模型的钢管与混凝土的补偿应变见表1。加载模型中,混凝土承担的荷载与其初始值相比降低了53%,钢管承担的荷载与其初始值相比则相应地增加了1.20 倍,由初值55 t 增加到122 t,有比较明显的内力重分布效应,如图4所示。通过补偿模型的测量结果剔除温度应变和收缩应变后,得到加载模型的徐变应变值,应变结果如图5所示。
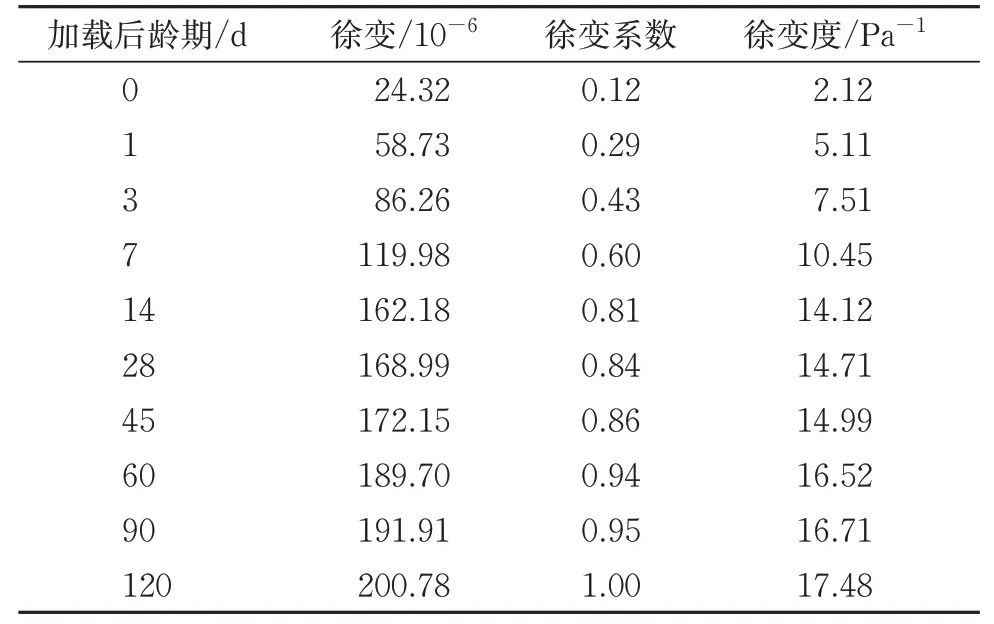
表1 加载14 d时钢管混凝土的徐变性能和补偿模型的应变
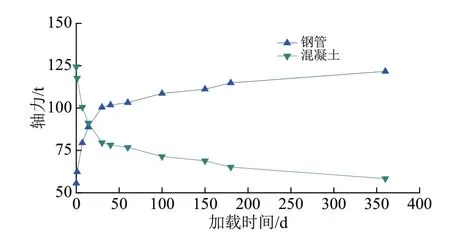
图4 模型试验中钢管和混凝土随时间发展的轴力
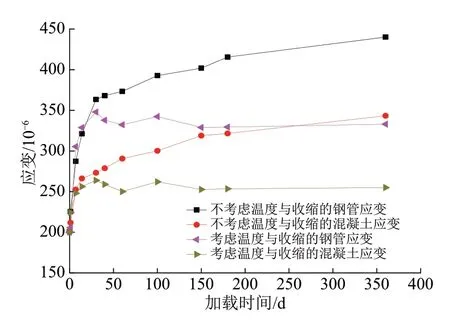
图5 模型试验中钢管和混凝土随时间发展的应变
把钢管混凝土材料视为1 种统一材料,分析钢管混凝土的徐变效应。相对于同龄期的素C60混凝土,钢管混凝土的早期徐变增长率相对平缓。根据徐变系数的定义[7],从模型试验数据得到360 d 时的钢管混凝土构件的徐变系数仅为1.20,而同龄期C60 混凝土的徐变系数则为2.22,可以看出加载模型的钢管混凝土的徐变系数约为普通C60混凝土徐变系数的53.6%。
3 钢管混凝土徐变系数
考虑管内混凝土徐变受钢管约束影响,从钢管混凝土构件的受力特点出发,基于混凝土弹性徐变理论,引入管内混凝土徐变影响受钢管约束的变形协调关系,采用的基本假定如下。
(1)管内混凝土为弹塑性材料,钢管为线弹性材料,两者之间黏结良好,变形满足平截面假定。
(2)线性徐变理论适用于管内混凝土,即徐变的应力增量与应变增量成正比关系。
(3)不考虑钢管的套箍约束效应,不考虑混凝土收缩与徐变之间的耦合影响。
从而得到考虑钢管约束的新的徐变系数φ′(t,τ0)[14-15]:
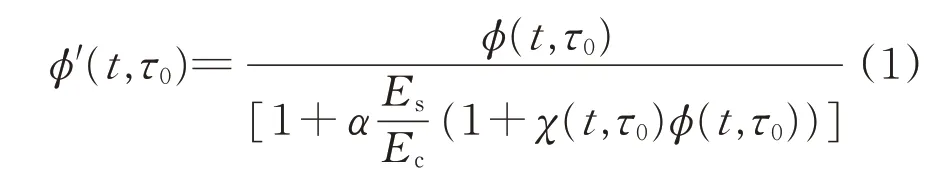
式中:φ(t,τ0)为素混凝土的徐变系数;Es和Ec分别为钢管和混凝土的弹性模量;χ(t,τ0)为混凝土的松弛系数;α为截面的含钢率。
式(1)是从钢管和混凝土变形协调以及钢管混凝土内力重分布的特点出发,得到的考虑钢管约束作用的新的钢管混凝土徐变系数。该公式能反映钢管混凝土构件的徐变,除了有普通混凝土徐变相同影响因素外,钢和混凝土的弹性模量比、含钢率等参数也会不同程度影响钢管混凝土的荷载重分布和管内混凝土的徐变。
图6 和图7 分别给出了钢管和混凝土的应变试验结果与计算结果,由图6 和图7 可见:试验结果与理论计算值吻合较好,误差较小;模型试验的钢管应变与理论计算的钢管应变发展趋势相同,但模型试验的钢管应变要略大于理论计算的钢管应变;模型试验的混凝土应变与理论计算的混凝土应变发展趋势相同,但模型试验的钢管应变要略小于计算的混凝土应变。
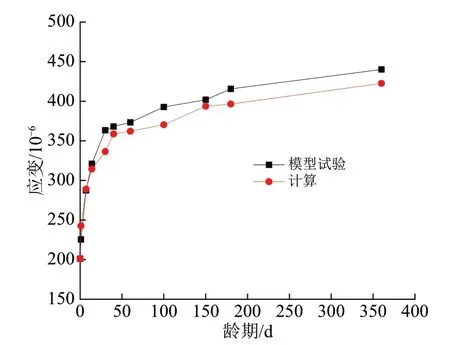
图6 钢管应变计算和试验结果
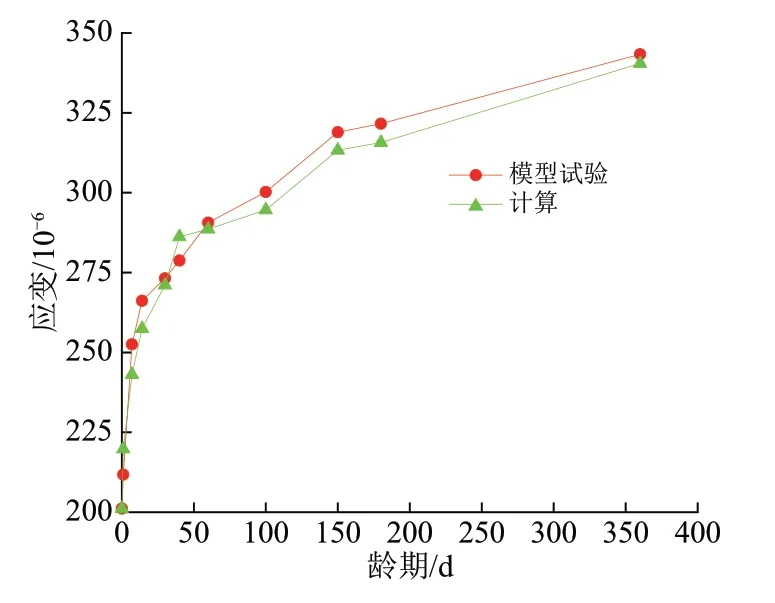
图7 混凝土应变计算和试验结果
4 实桥徐变效应
钢管混凝土拱桥的徐变计算采用按龄期调整有效模量法(AEMM)[7],该方法能考虑结构的形成过程,计算精度高。管内混凝土的徐变系数采用考虑钢管约束效应的新的徐变系数,即式(1)计算,实验模型计算参数和施工过程参照设计图纸进行选取。
计算分析过程考虑了拱肋形成过程中的构件的数量增减、混凝土的龄期特性、结构刚度、截面几何特性等参数的变化。当管内混凝土为液态时,混凝土当作外荷载分析,其弹性模量为0;混凝土固结后其弹性模量按0.8Ec计算。计算采用分离式计算模型[10,16],即把钢管与混凝土分别作为独立的梁单元,在共用的节点处保持二者的节点自由度一致,管内混凝土的徐变效应通过节点变形协调条件来实现。
按灌注混凝土的施工工序划分时间段,起始时刻为t1,后续时刻依次为t2,t3,···tn,相应的时间段 为: Δt1=t2-t1, Δt2=t3-t2, … , Δtn=tn+1-tn。每个时间段结束时进行1 次迭代计算,计算出相应的单元应力增量和节点位移增量。
4.1 管内混凝土弹性模量的影响
为了对比不同混凝土弹性模量对分析结果的影响,混凝土弹性模量分别取42.5 和36.0 GPa,且考虑徐变系数分别取式(1)与普通混凝土的徐变系数共计4个工况进行分析。具体工况如下。
工况1:混凝土弹性模量取36.0 GPa,徐变系数采用普通混凝土的徐变系数计算。
工况2:混凝土弹性模量取为36.0 GPa,徐变系数采用式(1)计算。
工况3:混凝土弹性模量取为42.5 GPa,徐变系数采用普通混凝土的徐变系数计算。
工况4:混凝土弹性模量为42.5 GPa,徐变系数采用式(1)计算。
恒载作用下3 a 后该桥拱肋的4 个工况的挠度如图8 所示。从图8 可以看出:工况1 下大桥的跨中挠度为42.4 mm,工况2 下大桥的跨中的挠度结果为44.4 mm,工况3 的跨中挠度为42.6 mm,工况4 的跨中的挠度为43.6 mm。混凝土弹性模量的取值对挠度的影响不甚明显,这是因为钢管的弹性模量起主要作用,混凝土弹性模量的作用相对较小。
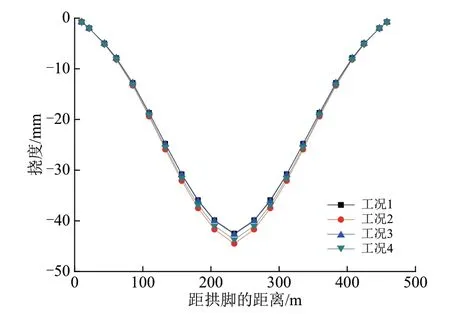
图8 大桥拱肋3年后的挠度
拱脚与拱顶的上、下弦管的混凝土压应力随龄期变化情况分别如图9—图12 所示。4 个工况下的混凝土应力的计算结果有较大的不同,这主要是混凝土弹性模量的取值不同所致。4 个工况下的钢管应力的计算结果基本一致。徐变系数采用式(1)计算得到的应力与采用普通混凝土的徐变系数计算得到的混凝土应力相比,在前60 d 时应力比较接近,后面就偏小;混凝土弹性模量取值大的工况,在前60 d时应力比较接近,后面就偏小。
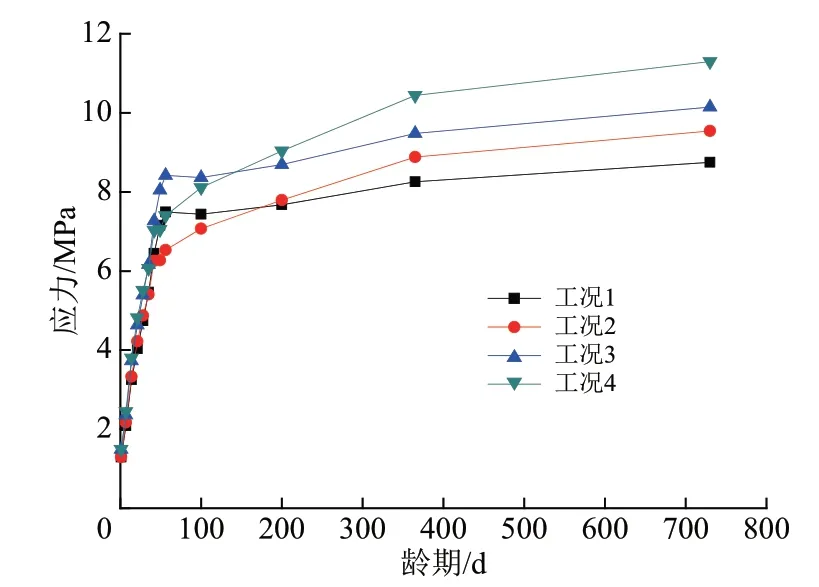
图9 拱脚上弦管的混凝土应力随龄期变化情况
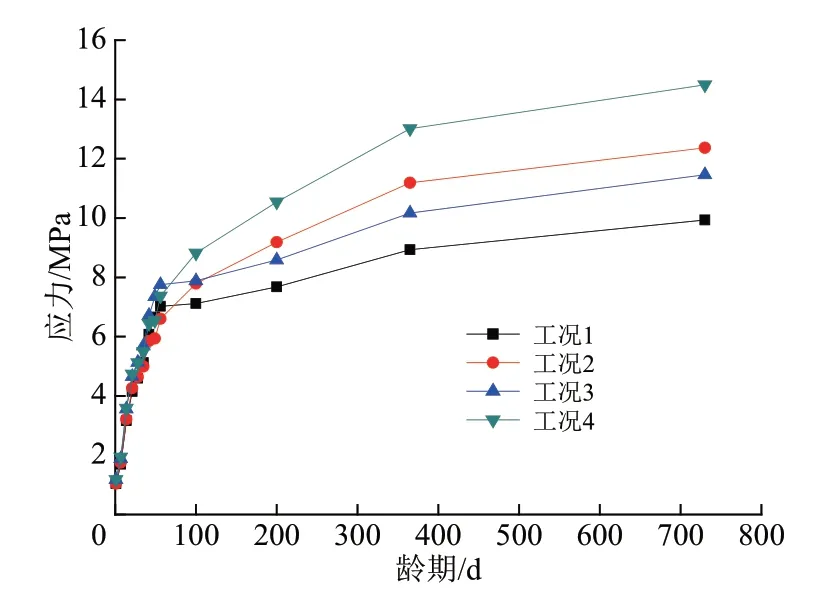
图10 拱顶上弦管的混凝土应力随龄期变化情况

图11 拱脚下弦管的混凝土应力随龄期变化情况
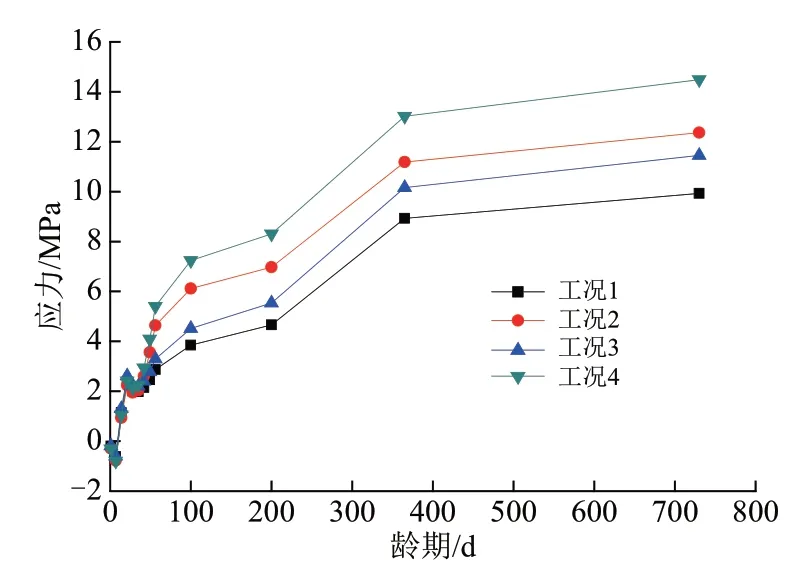
图12 拱顶下弦管的混凝土应力随龄期变化情况
大桥建成后3 a 后的拱肋上、下弦的钢管应力沿跨径分布如图13—图14所示。4个工况下的拱肋上弦钢管表面应力沿跨径分布情况的变化趋势总体一致,数值接近;不同数值的混凝土弹性模量对钢管应力影响较小,混凝土弹性模量的作用相对较小。4 个工况下的下弦钢管表面应力沿跨径分布情况基本一致。

图13 大桥建成后3 a后拱肋上弦钢管表面应力沿跨径分布情况
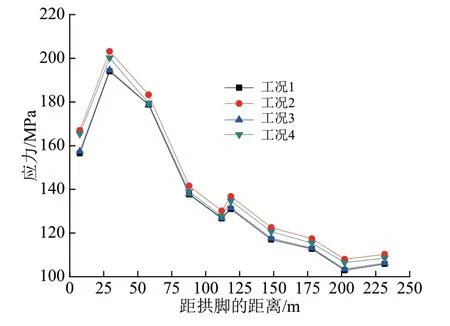
图14 大桥建成后3 a后拱肋下弦钢管表面应力沿跨径分布情况
4.2 几何非线性的影响
考虑几何非线性后,在工况2下的大桥拱肋3 a后的挠度见图15。由图15 可知,挠度由工况2 时的44.5 mm 变化到46.1 mm,增加3.6%。几何非线性对跨中挠度的增加不显著。
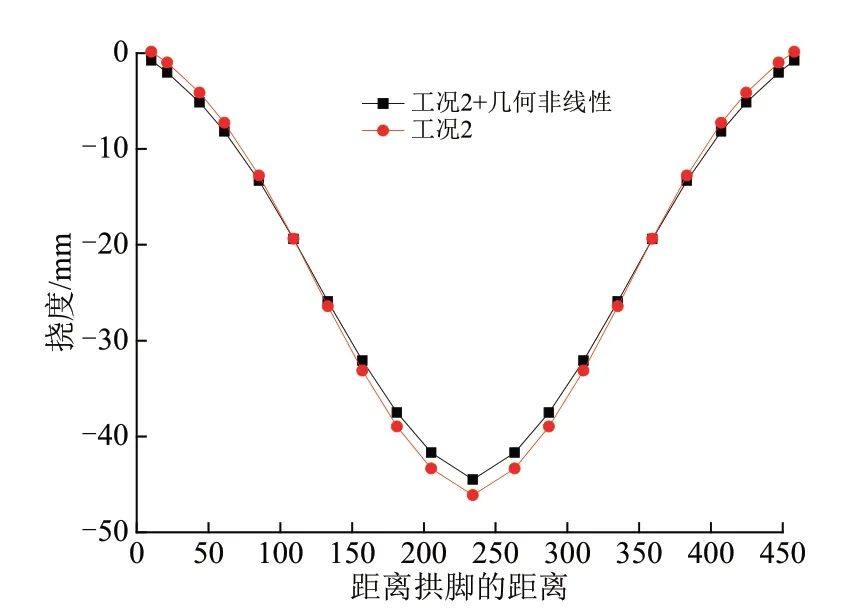
图15 考虑几何非线性后工况2 下拱肋3 a 后的挠度分布
考虑几何非线性后,在工况2 下的大桥拱肋上、下弦钢管压应力沿跨径分布情况如图16—图17 所示。考虑几何非线性后,拱肋不同截面受几何非线性的影响是不同的,其中拱脚上弦管的钢管应力增长9%,拱脚下弦管的钢管应力增长47%,但是拱顶的影响却很小。几何非线性对拱肋纵向不同部位的应力有不同程度的影响,其中拱脚部位影响最为明显。

图16 考虑几何非线性前后拱肋上弦钢管表面应力对比
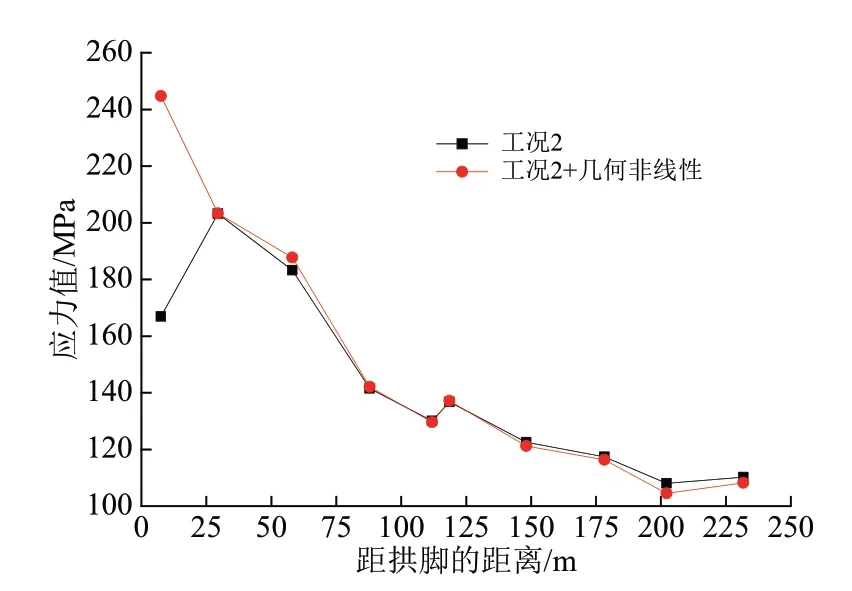
图17 考虑几何非线性前后拱肋下弦钢管表面应力对比
考虑几何非线性后,在工况2 下的大桥拱肋上、下弦钢管内的混凝土压应力沿跨径分布情况如图18—图19 所示。考虑几何非线性后,拱脚上弦管的混凝土应力增长43%,拱脚下弦管的混凝土应力增长30%,对混凝土的应力影响也较明显。几何非线性对拱肋纵向不同部位的应力有不同程度的影响,其中上弦钢管拱顶部位的应力却变小了,影响较为复杂。
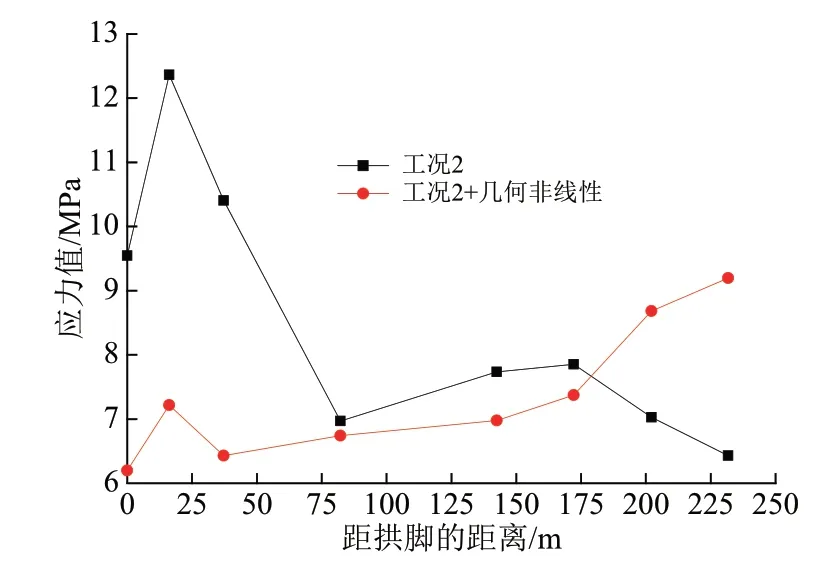
图18 考虑几何非线性前后拱肋上弦钢管内的混凝土应力对比
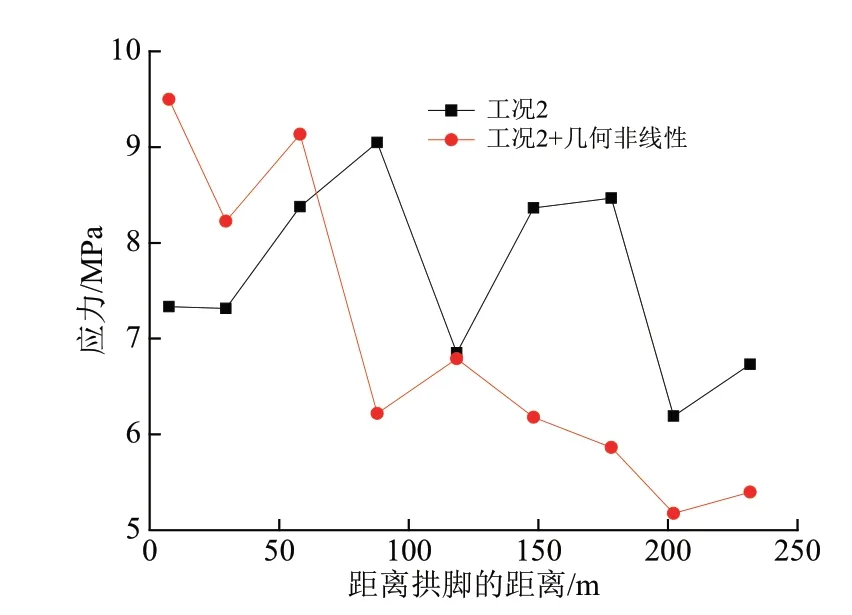
图19 考虑几何非线性前后拱肋下弦钢管内的混凝土应力对比
4.3 不同计算方法的区别
大跨拱桥成桥阶段计算分析一般采用内力叠加法,而施工阶段计算分析则采用应力叠加法[17]。应力叠加法是考虑各截面的形成过程,累计各施工阶段下的各截面的应力值。内力叠加法是在施工过程中累积各截面内力,再按成桥复合计算各截面受力。若不计施工中拱的弹性压缩和体系转换,内力叠加法就是全桥1次形成的1次加载分析[17]。
成桥3 a 后的拱肋上、下弦钢管和混凝土的应力随跨径分布情况分别如图20 和图21 所示。用2种方法分别计算得到的钢管应力结果之间差别较小。其中,2 种方法分别计算的上弦钢管应力最大区别位置在拱肋1/8 跨径处,差别约为16%;而2种方法分别计算的下弦钢管应力最大区别位置在拱肋1/4 跨径处,差别约为13%;用2 种方法分别计算得到的上、下弦钢管应力在1/8L截面至1/4L截面范围内区别较大,而拱脚至1/8L截面、1/4L截面至拱顶范围的钢管应力却总体区别较小。

图20 拱肋上、下弦钢管应力沿跨径分布
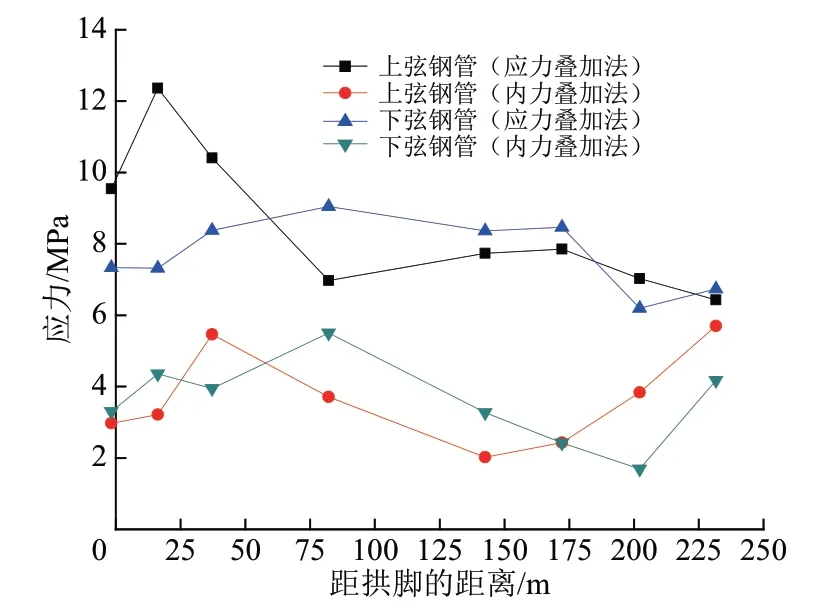
图21 拱肋上、下弦管内混凝土应力沿跨径分布
用2 种方法分别计算得到的管内混凝土应力结果之间有一定差别。其中,2 种方法分别计算的上弦管内混凝土应力最大区别位置在拱肋1/8 跨径处,差别约为40%;而2种方法分别计算的下弦管内混凝土应力最大区别位置在拱肋1/4 跨径处,差别约为39%。当然由于混凝土应力较小,比值差别大并与意味着区别明显。由内力叠加法得到的管内混凝土应力总体上均小于应力叠加法得到的管内混凝土应力。
5 实桥实测值与有限元计算值的对比
从拱肋施工开始,该桥就开始测量关键截面的钢管与混凝土的应力,积累了应力实测数据。限于篇幅,本节仅列举有代表性的2 号弦管应力与管内混凝土应力的测量值与计算值的结果。
图22—图23 显示了2 号弦管的钢管与混凝土的应力实测值与计算值的对比。从图22 可知,钢管应力的计算值与实测值较为接近,其中在工序10 下,跨中截面钢管应力的计算值为88.1 MPa,而实测值为91.8 MPa;在北岸拱脚截面,钢管应力的实测值为73.9 MPa,计算值为77.9 MPa,均较为一致;2 号弦管的钢管应力的计算值与实测值变化趋势一致,都随工序的增加而增加,且二者的数值比较接近。
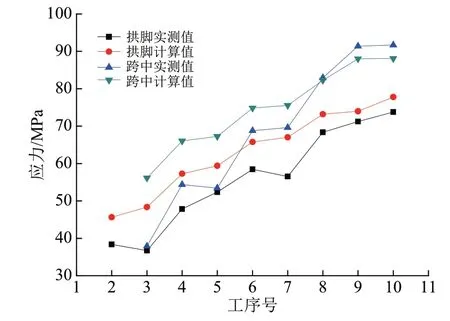
图22 拱肋2号弦钢管的测量值与计算值对比
从图23可知,混凝土应力的与计算值与实测值却存有较大差别。计算结果显示随施工工序递增,混凝土应力有变大的趋势,其中最大值位于拱脚截面,压应力最大计算值为7 MPa,但混凝土应力的实测结果则相对复杂许多,有拉压应力交替出现,但数值较小,实测最大压应力不超过4 MPa。混凝土应力的数值较小,外部因素(如温度变化、测量误差等)对其有较大影响。而钢管应力的数值较大,测量误差的影响程度相对较小,与计算值接近。
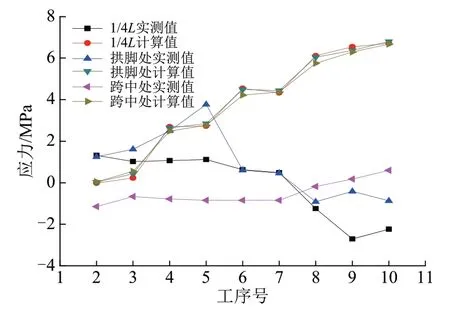
图23 拱肋2号弦管混凝土的测量值与计算值
6 结 论
(1)钢管混凝土构件的早期徐变效应显著,存在明显的荷载重分布现象。试验模型在180 t 荷载持续加载1 a 后,钢管承担的荷载增加了1.2 倍,混凝土承担的荷载则相应地下降了53%。
(2)从实桥的实测应力数据可以看出,由于徐变效应,随着时间的增长,特大跨钢管混凝土拱桥中钢管的应力增加,混凝土的应力减少。钢管应力的实测值与计算值总体一致,数值较大,变化趋势相同,但是管内混凝土应力的实测值与计算值之间存在差别,且实测值相对复杂。
(3)在目前钢管混凝土结构的设计规范中,高强度钢材往往要搭配高标号混凝土,这对初应力较小的钢管混凝土结构是合适的,但对初应力较大的大跨度钢管凝土拱桥而言,拱肋需要高型号钢材,但管内混凝土的应力较小,不需要高标号的混凝土,而且通过有限元与现场实测计算发现,混凝土的弹性模量对全桥的刚度影响不大。
(4)钢管混凝土的徐变系数大多在试验室条件下得到,但由于实桥的复杂性,可能会导致试验结果与实桥徐变之间存在较大误差,从而使徐变有限元分析与实桥测量结果之间存在差别。
