基于涡流检测和神经网络的钢轨表面滚动接触疲劳裂纹特征评估
2021-10-19熊龙辉张玉华马运忠钟艳春黄筱妍
熊龙辉,张玉华,马运忠,李 培,钟艳春,黄筱妍
(1. 中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081;2. 北京铁科英迈技术有限公司,北京 100081)
由于车轮踏面与钢轨表面的滚动接触,在钢轨表面和轨距角处容易形成鱼鳞状的滚动接触疲劳裂纹(Rolling Contact Fatigue Crack,RCF)[1]。RCF一般沿着钢轨变形流线方向扩展,随钢轨材料的塑性变形深度不断增大,会逐渐转变为沿着钢轨纵向方向发展。在车轮反复作用下,RCF 一般会发展为2~4 mm 深的剥离掉块。在速度等级大于160 km·h-1的线路,剥离掉块的长度超过25 mm 且深度超过3 mm 即判为钢轨重伤。剥离掉块底部若存在残余裂纹,该裂纹可能发展为轨头横向疲劳裂纹,且有向轨底方向扩展的趋势,该类伤损危害性大,易导致横向断轨事故,严重影响铁路运输秩序和安全[2-3]。
我国铁路工务部门在钢轨探伤时主要采用超声波技术对钢轨内部伤损进行检测[4],其后对钢轨表面出现RCF 后是否进行打磨维护或换轨处理主要依靠经验确定,现场缺乏有效的钢轨RCF 深度和角度特征评估。涡流检测技术可用于钢轨表面RCF 检测,德国、荷兰等国采用涡流检测技术评估钢轨表面RCF 的位置和深度,并将涡流检测系统安装在钢轨检测车和手推式仪器上[5-7]。我国也在钢轨裂纹的涡流检测和定量评估方面开展了大量研究:华南理工大学张思全等通过研究基于小波去噪的自然裂纹涡流检测信号处理方法,有效提取噪声中的缺陷信号[8];中国铁道科学研究院黄凤英通过仿真分析和指数函数拟合方法研究了涡流检测中钢轨表面伤损的深度评估方法[9];浙江大学彭谢丹研究了脉冲涡流检测中基于支持向量机和D-S证据理论的RCF评估方法,并对角度为45°,60°和90°的斜裂纹进行了评估[10];李国厚等在涡流检测中采用减聚类算法RBF 神经网络对基于巨磁阻的钢轨表面缺陷深度定量评估进行了研究[11]。目前对钢轨RCF 的定量评估方法是针对裂纹的单一参数进行评估,缺乏对裂纹角度和深度的多参数特征评估。
本文通过涡流检测系统采集钢轨表面人工伤损信号,研究裂纹伤损深度和角度参数的信号表征特征,为进一步推动钢轨RCF 的特征评估提供新理论依据和试验方法。
1 试验条件
1.1 人工伤损
为验证不同激励频率下的涡流检测对钢轨表面RCF 评价参数的影响,根据常见钢轨表面RCF 形貌,在钢轨轨距角处加工了长度为5 mm,与钢轨纵向夹角为45°的2 组人工伤损,其中,一组与水平面夹角为30°,深度分别为0.35,0.50,1.00,1.50,2.00,2.70,3.50 和5.00 mm;另一组深度为2.70 mm,与水平面夹角分别为5°,10°,15°,30°,45°和90°。人工伤损示意图如图1所示。
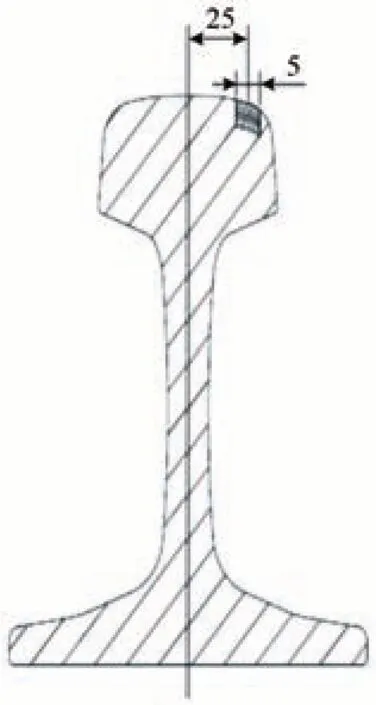
图1 人工伤损示意图(单位:mm)
1.2 涡流检测系统
钢轨表面RCF 涡流检测系统组成如图2 所示。系统采用单通道笔式放置式探头,其内部为带有磁芯聚焦磁场的线圈,如图3所示。试验时前置放大增益设置为15 dB,可调增益放大器增益设置为37 dB,对信号进行截止频率为2 Hz的高通滤波。
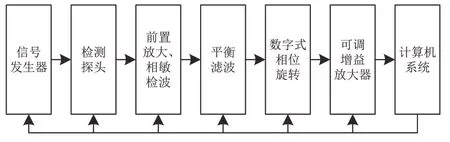
图2 涡流检测系统组成
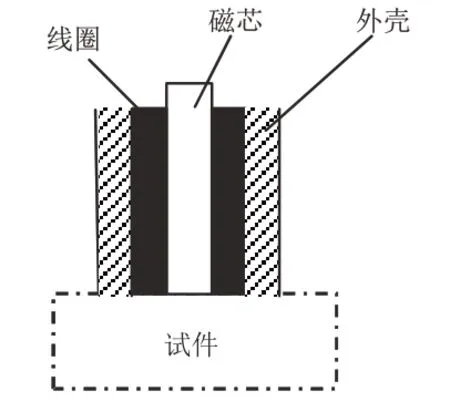
图3 放置式探头
涡流检测系统输出信号为探头阻抗等效电压,下文对其幅值(包括实部和虚部)、X分量和Y分量进行特征值研究。某一人工伤损信号的阻抗分解示意图如图4 所示。图中:X分量为探头阻抗实部;Y分量为探头阻抗虚部。
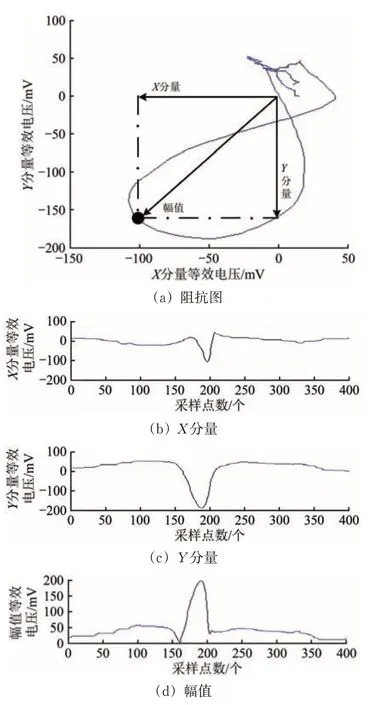
图4 阻抗分解示意图
2 不同激励频率下涡流检测试验
涡流检测中影响阻抗变化的因素包括激励频率、钢轨材质(电导率和磁导率)及缺陷参数(长度和深度)。实际检测中钢轨材质不变,只有激励频率和缺陷参数会对阻抗产生影响[12]。为选择合适的激励频率,共进行7 组试验,激励频率分别设置为100,303,500,769,1 000,1 429 和2 000 kHz。每组试验中需调节信号相位,使提离效应只影响阻抗信号的X分量。采集数据时,探头从深度为0.35 mm 至5.00 mm 的人工伤损依次移动,每组试验对人工伤损进行5次检测。
某一激励频率下探头对不同深度人工伤损的检测信号如图5 所示。由图可见:通过人工伤损X分量信号峰值难以区分人工伤损的深度;Y分量信号谷值随人工伤损深度增加逐渐变大;对人工伤损深度的辨识,Y分量比X分量有明显对应关系,所以选取Y分量信号谷值作为评价缺陷深度的特征。

图5 不同深度人工伤损对应的X分量、Y分量和幅值信号
每组试验中,提取8 个不同深度人工伤损信号的Y分量信号谷值特征,剔除5次检测中同一人工伤损信号Y分量谷值的最大值和最小值,对剩余3次Y分量信号谷值取平均值,得到不同深度人工伤损Y分量信号谷值随激励频率变化规律如图6所示。

图6 不同深度人工伤损Y分量信号谷值随激励频率变化规律
由图6可知:激励频率在0~769 kHz范围内Y分量信号谷值均随激励频率的增大而增大,激励频率在769~2 000 kHz范围内Y分量信号谷值随激励频率的增大而减小,这是由于涡流检测具有趋肤效应,当激励频率增加到一定程度后,涡流场随钢轨深度增加而快速减小,对较深伤损难以区分其深度;涡流检测激励频率减小时,虽然涡流场渗透深度增大,但是会使探头线圈阻抗变化减小,影响检测灵敏度。
通过上述试验可知,激励频度为769 kHz 时,不同深度伤损信号谷值均较大,可得到较高的信噪比。
3 人工伤损深度和角度评估
基于最佳激励频率769 kHz 下不同深度和角度的人工伤损涡流检测结果,分别采用曲线拟合和神经网络模型,对人工伤损的深度和角度进行评估,并比较定量评估分类准确率。
3.1 拟合曲线
分别采用指数函数和三次多项式函数对伤损深度和角度数据进行最小二乘法曲线拟合,得到指数函数和三次多项式函数评估模型分别为
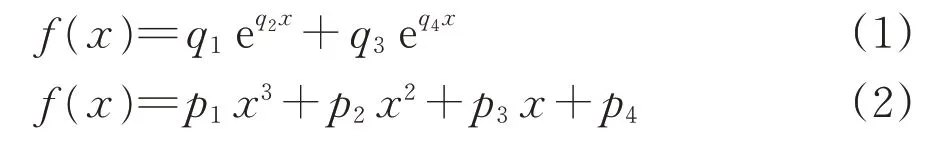
式中:x为缺陷尺寸参数(深度或角度);f(x)为信号特征值;q1,q2,q3和q4为指数函数求解系数;p1,p2,p3和p4为三次多项式函数求解系数。
3.1.1 伤损深度评估
图5 所示以伤损的Y分量信号谷值和幅值信号峰值作为特征值,分别采用指数函数和三次多项式函数进行最小二乘法曲线拟合,结果如图7 所示。由图7 可知:当伤损深度在0~2.70 mm 范围时,特征值随缺陷深度增加而增大,且增大趋势逐渐变缓;当伤损深度在大于2.70 mm 时,特征值大小基本不变,这是因为涡流检测中集肤效应的影响,当伤损深度大到一定程度后,伤损深度的增加对涡流信号影响很小。

图7 伤损深度评估曲线拟合
人工伤损的Y分量信号谷值和幅值信号峰值拟合参数见表1。

表1 深度评估曲线拟合参数
由表1 可知:与幅值信号峰值特征和三次多项式函数拟合比较,提取人工伤损的Y分量信号谷值特征,采用指数函数进行最小二乘法曲线拟合时,SSE 和RMSE 参数均最小,R-Square 和AdjustedR-Square 参数均更接近1,可得到最优拟合曲线,表达式为

式中:d为伤损深度;f(d)为Y分量信号谷值。
3.1.2 伤损角度评估
769 kHz 激励频率下,不同角度人工伤损的检测信号如图8 所示。由图8 可以看出:随伤损角度变化,Y分量信号变化较小;伤损发展角度在5°~30°范围时,X分量信号谷值随发展角度增大而变小;角度为30°时,X分量信号谷值转变为峰值;角度在30°~90°范围时,X分量信号峰值随发展角度增大而变大。
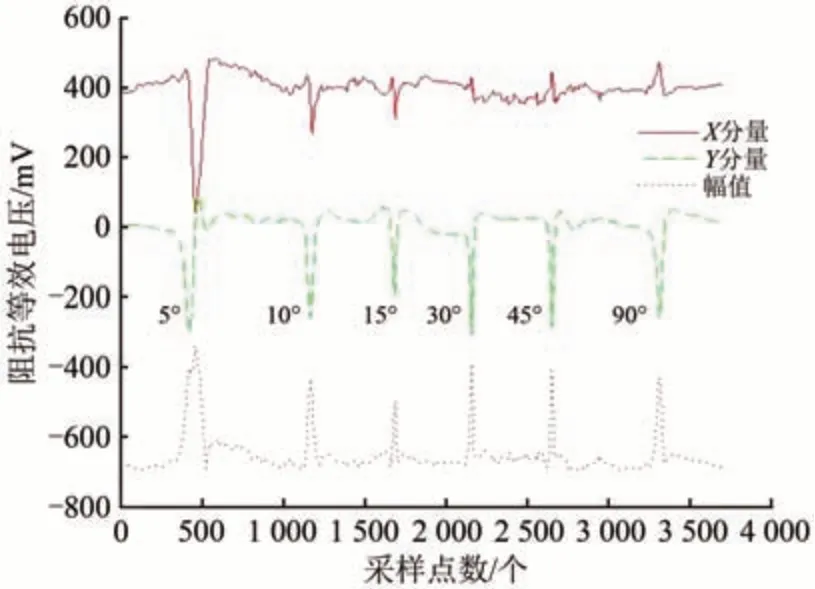
图8 激励频率为769 kHz的不同角度伤损检测信号
根据上述检测信号特点,如果缺陷X分量信号为谷值则提取其谷值数值R作为特征值,如果缺陷X 分量信号为峰值则提取其峰值数值R作为特征值;提取X分量R值及其与Y分量谷值之比作为特征值,分别采用这2 个特征值评价伤损角度,并采用指数函数公式(1)进行最小二乘法曲线拟合,结果如图9所示。

图9 伤损角度评估指数函数曲线拟合
由图9可知:伤损角度在5°~30°范围时,特征值随角度增大而增大;伤损角度在30°~90°范围时,特征值随发展角度的增大也呈增大趋势,但是变化很微小。
试验表明,伤损角度较小时,采用X分量R值及其与Y分量谷值之比作为特征值可以较准确地评估角度大小。
伤损的X分量R值及其与Y分量谷值之比拟合参数见表2。由表2 可知:2 个特征值参数的数量级不一致,所以SSE 和RMSE 作为误差参数不做参考;提取X分量R值作为特征值,计算所得的R-Square 和AdjustedR-Square 参数更接近1,得到最优拟合曲线,其拟合曲线公式为


表2 发展角度评估指数函数曲线拟合参数
式中:a为伤损角度;f(a)为X分量R值。
3.2 神经网络模型
通过上文曲线拟合分析发现,对于深度大于2.70 mm 的伤损,涡流检测难以区分伤损深度参数;对于角度大于30°的伤损,涡流检测难以区分伤损角度参数。分别对伤损深度和角度进行等级分类,采用BP 神经网络模型对伤损参数进行分类训练,将深度分为4 类,角度也分为4 类,伤损分类训练等级表见表3。

表3 伤损分类训练等级表
训练模型如图10 所示。由图10 可见:采用输入层、隐藏层和输出层各为1 层的3 层BP 神经网络;隐藏层神经元个数为10个,激活函数为TANSIG;输出层神经元个数根据分类数量设计为4个,激活函数为LOGSIG。

图10 缺陷尺寸参数评估BP神经网络训练模型
LM 算法对训练过程中过参数化问题的不敏感性,使其能够很好处理冗余参数的问题,减少代价函数陷入局部最小值的可能性,LM 算法兼具牛顿法和梯度法的优势,是一种介于牛顿法和梯度法之间的非线性优化方法,所以本文采用LM 算法进行训练。
3.2.1 伤损深度评估
分别对每个不同深度的人工伤损进行5 次检测,8 个伤损共提取40 组伤损信号特征值,分成32组训练数据和8组测试数据。特征值包括Y分量信号谷值和幅值信号峰值,将提取的不同深度伤损特征值作为BP 神经网络的输入。将每组特征值对应的伤损按表3 分类,分类对应输出作为BP 神经网络的输出。采用32 组训练数据对上文设计的BP神经网络进行训练,得到伤损深度评估模型。
3.2.2 伤损角度评估
对6 个不同角度的人工伤损分别进行5 次检测,得到30 组伤损信号特征值,分成24 组训练数据和6 组测试数据,特征值包括X分量R值及其与Y分量谷值之比,将提取的不同角度伤损信号特征值作为BP 神经网络的输入。将每组特征值对应的伤损按表3 分类,分类对应输出作为BP 神经网络的输出。采用24组训练数据对上文设计的BP 神经网络进行训练,得到伤损角度评估模型。
3.3 定量评估分类结果对比
根据伤损深度和Y分量信号谷值的关系即式(3),参照表3 伤损深度等级分类,可以得到不同深度对应的Y分量信号谷值的等级。将8组测试数据的Y分量信号谷值按曲线拟合关系得到的分类测试结果见表4,曲线拟合深度定量评估分类准确率为75%。
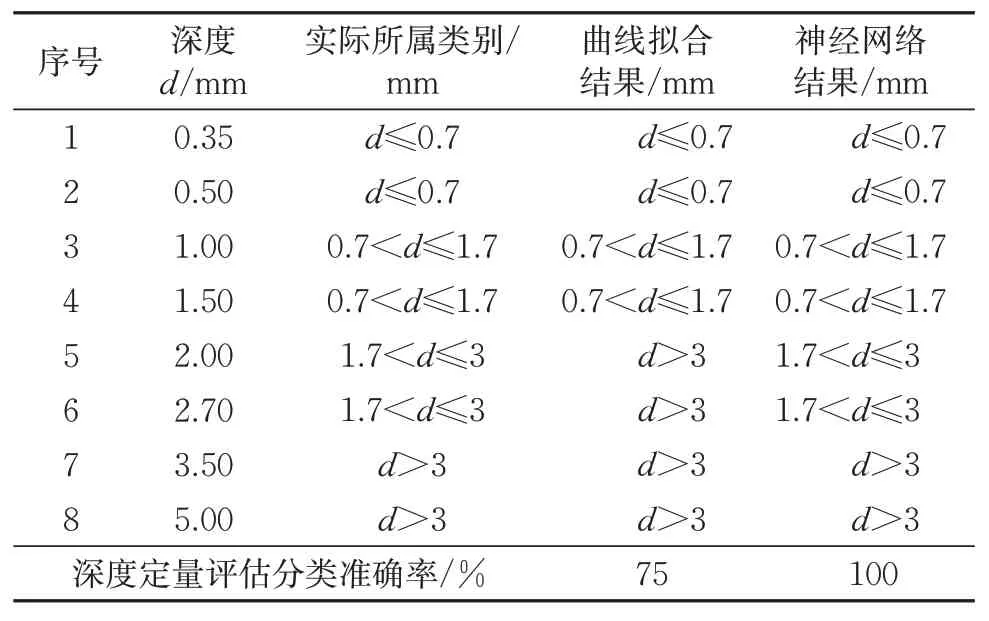
表4 神经网络和曲线拟合深度定量评估分类结果对比
采用BP 神经网络训练得到伤损深度评估模型,对8 组测试数据进行验证,得到伤损深度所属类别结果见表4,训练得到的神经网络模型对8 组测试数据深度定量评估分类准确率为100%。
根据伤损角度和X分量R值关系即式(4),参照表3 伤损角度等级分类,可以得到不同角度对应的X分量R值的等级。将6 组测试数据的X分量R值按曲线拟合关系得到的分类测试结果见表5,曲线拟合角度定量评估分类准确率为66.67%。

表5 神经网络和曲线拟合角度定量评估分类结果对比
采用BP 神经网络训练得到伤损角度评估模型,对6 组测试数据进行验证,得到伤损角度类别结果见表5,训练得到的神经网络模型对6 组测试数据角度定量评估分类准确率为83.33%。
通过曲线拟合与神经网络模型对伤损分类准确率的比较可知,采用神经网络模型进行伤损深度和角度分类准确率均高于曲线拟合模型分类准确率。
4 结 论
(1)基于钢轨涡流检测技术,研究了不同激励频率对人工伤损检测信号的影响,得到放置式探头的最佳激励频率为769 kHz。
(2)采用曲线拟合方法研究了人工伤损深度和角度的涡流检测信号特征表征方法,得出选取探头阻抗虚部信号谷值表征伤损深度,选取探头阻抗实部信号R值表征伤损角度。对于深度大于2.7 mm 的伤损和角度大于30°的伤损,涡流检测技术难以区分伤损尺寸参数。
(3)通过曲线拟合方法对伤损深度与角度划分了分类等级,建立了伤损评估BP 神经网络模型。通过与曲线拟合评估对比发现,采用BP 神经网络评估伤损深度和角度的分类准确率分别为100%和83.33%,均高于曲线拟合。
