图的算数-几何谱半径及能量的界

王 猗，高玉斌

(中北大学 理学院， 太原 030051)

1 研究现状

考虑的图均为简单无向图。设图G=(V(G)，E(G))为n阶、m条边的无向图，其顶点集为V(G)={v1，v2，…，vn}，边集为E(G)，|E(G)|=m。图G的最大度和最小度记为Δ和δ。

近年来，人们对于图能量的研究一直非常活跃[1]，其在化学研究中发挥着越来越重要的作用。由Gutman[2-3]引入的图的能量定义为图的邻接矩阵特征值的绝对值之和，它可以用来近似分子的总电子能量，在文献[4-6]中得到了一些图基于度能量的界。Shegehalli等[7]提出了图的算数-几何指数，定义了图G的算数-几何邻接矩阵。

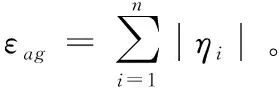
Zheng等[5]得出了算数-几何能量的一些上下界。受此启发，利用图的最大度、最小度以及图的一些拓扑指数得到图的算数-几何谱半径和算数-几何能量的一些新的上下界。

用到的拓扑指数包括：

第一Zagreb指数M1(G)[9]定义为

对称分割度指数SDD(G)[11]定义为

2 引理

引理1[12](Rayleigh-Ritz) 设B为n×n阶矩阵，其特征值为ρ1≥ρ2≥…≥ρn，对于任意的0≠x∈Rn，有

xTBx≤ρ1xTx

当且仅当x是B的对应于其最大特征值的特征向量时，等式成立。

引理2[13](Cauchy-Schwarz) 设ai，bi∈R，i=1，2，…，n，则对于任意的1≤i≤n，

当且仅当对于任意的1≤i，j≤n，aibj=ajbi时等式成立。

引理3设a，b∈R，a≥b≥0，则

当且仅当b=0时等式成立。

3 算数-几何谱半径的界

定理1设G为n阶连通图，边数为m，最小度为δ，则

(1)

证明设x=(x1，x2，…，xn)T为Rn中任意单位向量，由引理1、3，得到

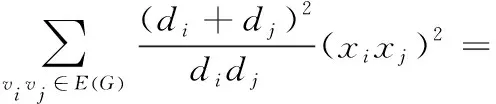
(2)

故

证毕。

定理2设G为m条边的n阶连通图，最小度为δ，则

(3)

证明由引理2可得

定理3设G为m条边的n阶连通图，最小度为δ，则

(4)

证明易知

SDD(G)+2m

由引理2知，不等式(4)成立。证毕。

4 算数-几何能量的界

(5)

故由定理1～3可知，下面关于算术-几何能量的下界定理是显然的。

定理4设G是n阶连通图，有m条边，最小度为δ，则

(6)

(7)

(8)

(9)

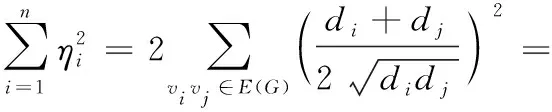
(10)

定理5设G为m条边的n阶连通图，则

(11)

其中

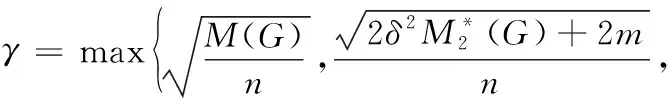
证明由引理2，令ai=1，bi=|ηi|，则对于2≤i≤n，有

(12)

再利用式(10)(12)，可得

(13)

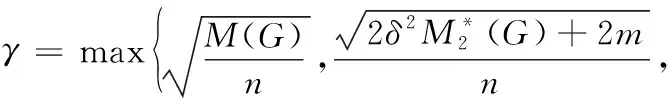
则由定理1～3，可得

证毕。

定理6设G为m条边的n阶连通图，最大度和最小度分别为Δ和δ，则

(14)

其中

证明易知

(15)

利用式(10)(12)，可得

考虑函数

易知，当

时，f2(x)单调递减。故由定理1～3可知，不等式(14)显然成立。证毕。

在下面2个定理中，得到了二部图算术-几何能量的上界。

定理7设G为m条边的n阶连通二部图，则

(16)

其中

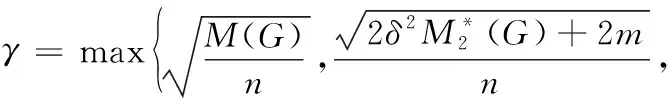
证明如果G为n阶连通二部图，则ηi=-ηn-i，i=1，2，…，⎣n/2」，由引理2可得

(17)

结合式(10)(17)，得

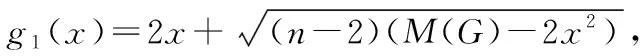
定理8设G为m条边的n阶连通二部图，最大度和最小度分别为Δ和δ，则

(18)

其中

证明由式(10)(15)和(17)可得

设函数

显然，当

时，g2(x)单调递减。故根据定理1～3可知，不等式(18)成立。证毕。