隧道开挖和爆破扰动耦合作用下埋地管道安全性研究
2021-10-18彭梦龙施成华陈家旺
彭梦龙, 施成华,2, 陈家旺
(1. 中南大学 土木工程学院, 长沙 410075; 2. 重载铁路工程结构教育部重点实验室, 长沙 410075;3. 广州地铁设计院有限公司, 广州 510010)
埋地管道是水、石油、天然气等物资的主要运输方式,在生产生活中扮演着不可替代的角色。与此同时,城市轨道交通等基础设施的建设正如火如荼的进行着,这些工程项目不可避免的对临近管道产生影响,稍有不慎就会导致管道破坏,进而严重影响人们的生产生活。
在这样的背景下,国内外学者对埋地管道的安全性进行了大量的研究[1-2]。Konuk[3]将管道变形视为管土耦合模型的横向屈曲问题,基于文克尔地基梁模型,利用经典杆理论建立了管道二维屈曲问题的理论公式,得到了管土相互作用下管道侧向屈曲参数以及管道应力计算方法。Marshall等[4]采用离心机模型试验,探究了隧道开挖变形对埋地管道的影响机理;Klar等[5]通过线性等效方式对土壤的非线性特性进行模拟,提出了新的管道安全性评估方法,实现了隧道位移和管道弯矩的关系预测;Shi等[6]通过离心机试验,研究了地表和管道在隧道开挖下的三维响应,并根据试验数据修正了相关的管道三维响应计算公式。吴铭芳[7]以质点振动速度为研究对象,研究了隧道爆破施工对临近输油管道的影响范围,并结合爆破安全规程,对石油管道进行了结构安全评价。舒懿东等[8]以西成客专仙女岩隧道出口段爆破作业为背景,运用有限元软件模拟埋地管道在爆破振动下的动力响应,以此为基础研究了管道埋深对管道的动力响应的影响特征。Jiang等[9]以北京地铁16号线为工程背景,基于量纲分析法建立了预测地表振速的理论模型,并进一步建立数值模型分析不同爆破参数下地铁隧道爆破对燃气管道的影响。郝郁清[10]建立管土三维有限元模型揭示了不同参数对于爆破振动时管道动力响应的影响,通过分析管道应变与振速之间的数值关系、管道与其正上方地表峰值振速之间的数值关系,明确了管道正常运行时的最小安全距离以及最大安全允许振速。
综合上述文献分析可知,国内外学者从理论计算、建模分析、模型试验、现场监测等多个方面对埋地管道进行了研究,埋地管道的安全性得到广泛关注并积累了丰富的研究成果。但既有研究大多基于爆破荷载、地层变形等单一因素研究管道安全性问题,针对两者耦合作用下埋地管道安全性的研究还鲜有报道。因此,笔者以深圳市南坪三期大山陂1号隧道接近油气管道施工为工程背景,对隧道开挖变形及爆破扰动耦合作用下临近埋地管道的安全性进行了研究。
1 数值模型建立
1.1 工程概况
深圳市南坪快速路三期工程大山陂水库1号隧道位于马峦山郊野公园内,隧道从大山陂水库南侧水源保护区外围绕过,穿越水库南侧山体。左右隧道均为单洞四车道,设计行车速度为80 km/h,隧道内轮廓为五心圆拱形式,采用矿山法施工。
DN800高压燃气管沿隧道左线北侧敷设,隧道距离高压燃气管道最近处(位于ZK13+680里程)平面距离约6.4 m远,该位置隧道埋深约为32 m,距隧道出口明暗分界处(ZK13+730里程)仅55 m,如图1所示。DN300成品油管道沿隧道左线由西北往东南敷设,隧道距离成品油管道最近处(位于隧道出口明暗分界处ZK13+730)平面距离约为27 m,两者交叉部位的隧道最小埋深约为32 m。
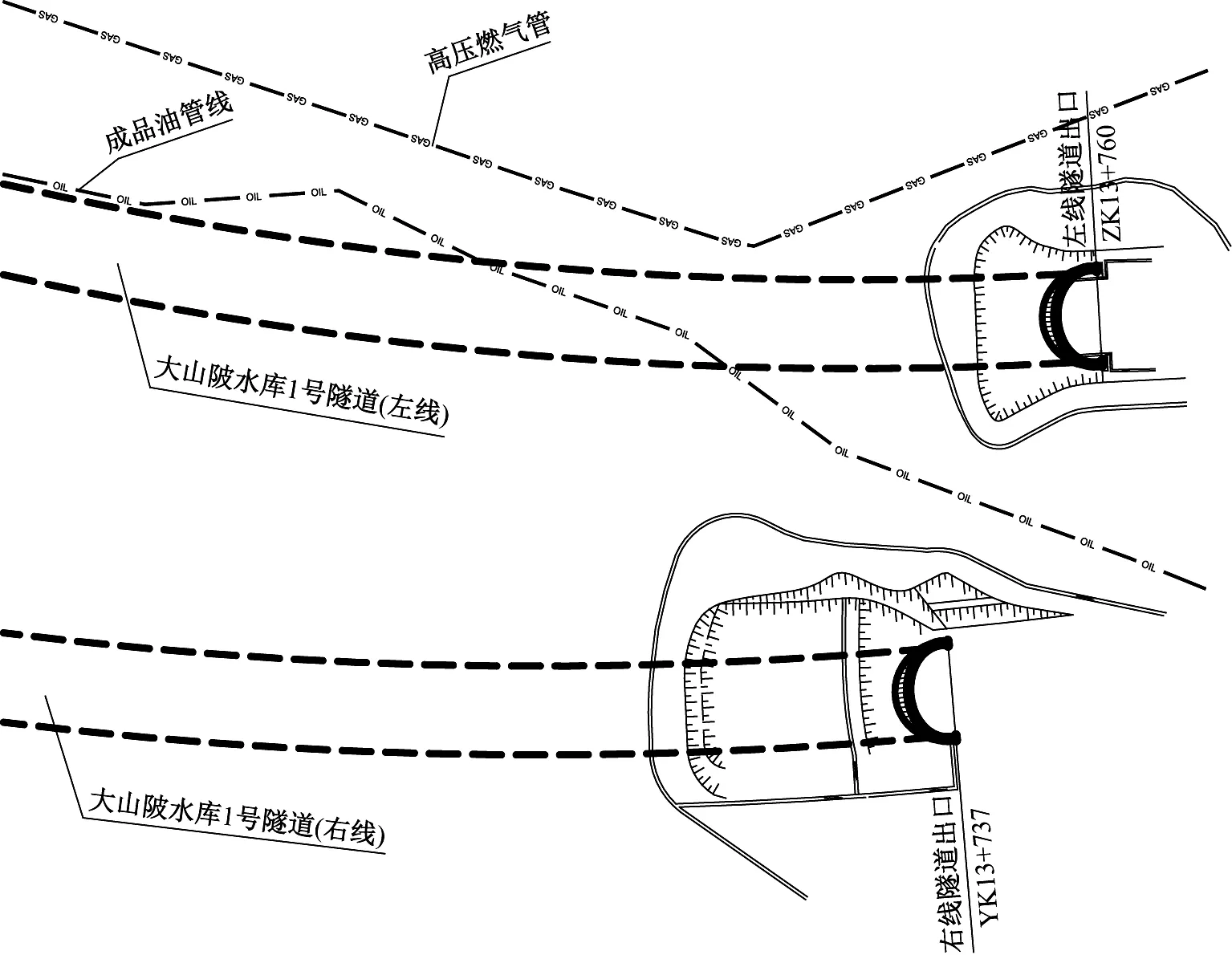
图1 隧道与管道平面位置关系
1.2 材料参数
开挖变形导致管道的应力重分布属于静力问题,而爆破荷载对管道的影响是动力问题,故模型采用隐-显式顺序求解。
大量实践经验[11-13]可证明,采用双线性随动强化模型能较好的反应材料的弹塑性变形特性,因此采用该模型模拟岩体和管道的本构关系。岩体和管道的材料参数如表1和表2所示。

表1 岩体材料参数

表2 管道材料参数
Drucker-Prager弹塑性模型[14-15]考虑了材料的剪切膨胀特性,能够更加真实的反应土体的黏弹性特征。其表达式为
(1)
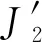
因此,为了在保证模型准确性的同时提高计算速度,采用该模型模拟地表土体的本构关系。土体的材料参数如表3所示。

表3 土体材料参数
1.3 爆破荷载模拟
为体现多段炸药的爆破叠加效应,从而更加真实地反映出爆破远区的震动特性,黄亚兵[16]在单段爆破曲线的基础上提出了全时程爆破荷载曲线,结果证明其模拟的结果接近实际工程的监测值。其表达式为
(2)
(3)
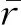
因此,模型根据爆破监测的实际微差间隔时间及单段装药量等数据将单段爆破荷载曲线叠加为全时程爆破荷载曲线以模拟爆破荷载的作用。某一全时程爆破荷载曲线示意图,如图2所示。
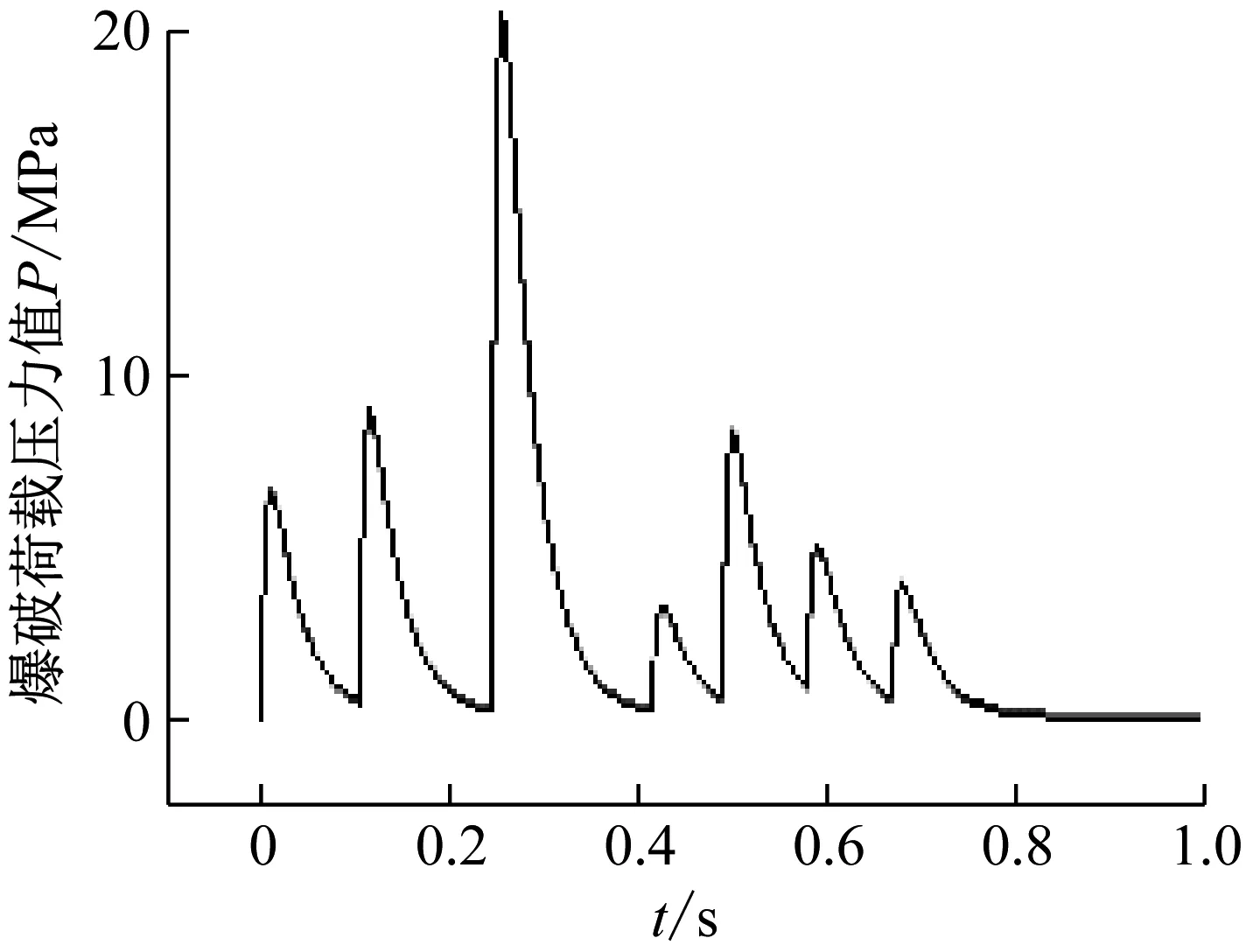
图2 爆破荷载曲线示意图
1.4 边界条件
在隐式分析时,约束模型底部竖向位移、管道两端的纵向位移和模型四周的水平位移。在显示分析时,为避免采用隐式分析的边界条件所引起的应力波反射现象,在显式分析阶段除了模型顶面以及隧道开挖轮廓面设置为自由边界外,选择SOLID164实体外表面组成所需边界的节点通过EDNB命令在这些节点上施加无反射边界以消除应力震荡的现象。
1.5 模型建立
建立管-土-隧动静耦合作用分析模型,如图3所示。模型整体尺寸为170 m×75 m×10 m,管道埋深为1.5 m,隧道埋深为15 m,其中地表至其下3 m为粉质黏土,隧道围岩为泥砂岩。隐式阶段采用SOLID185单元模拟模型中的岩石、土体及管道,显式阶段将其转换为SOLID164单元,采用自动网格划分技术对模型几何进行划分。
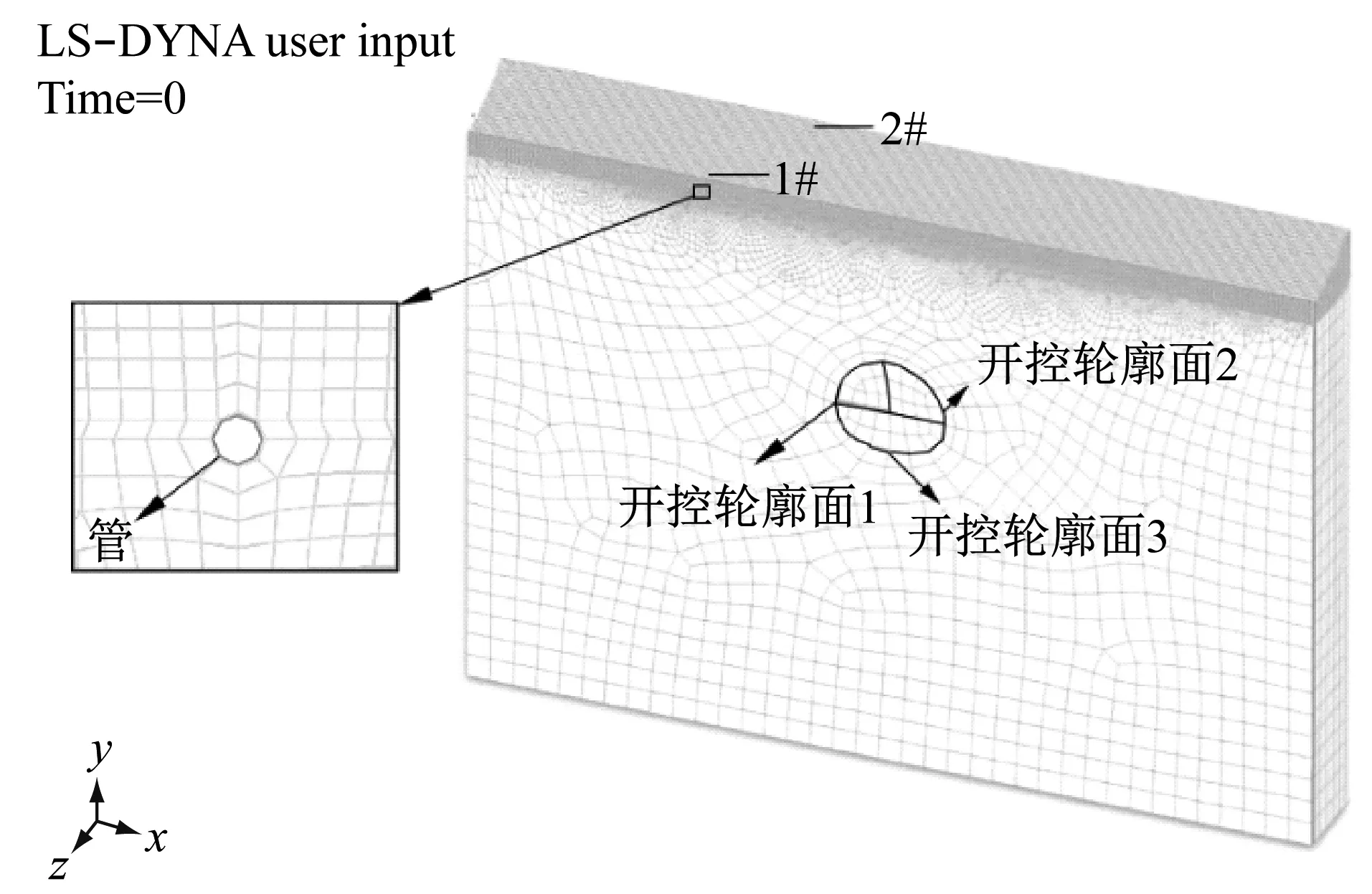
图3 管-土-隧动静耦合作用分析模型
1.6 模型验证
为保证隧道爆破时管道的运营安全,在管道上方地表处设立了监测点,利用爆破测振仪对现场进行实时监测。由于传感器的实际布置方向和数值模型中各个坐标轴不可能完全重合,因此采用两个测点的合速度验证模型的可靠性,对比结果如图4所示。
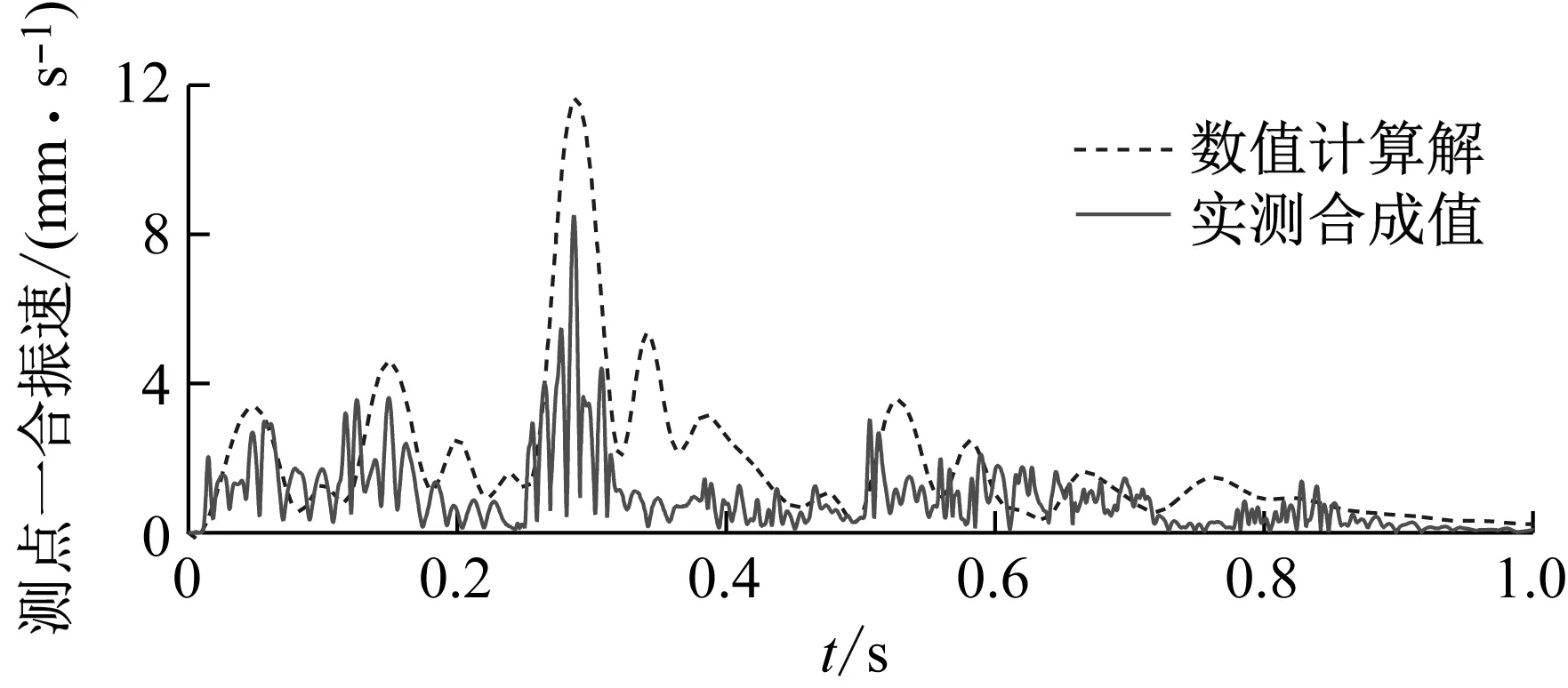
(a)
从实测值和计算值的对比可知,两者的变化规律基本吻合。由于采用微差爆破技术,实测值曲线出现了较为明显的7个峰值,模型采用了全时程爆破荷载曲线模拟微差爆破,也反映了这种峰值变化情况,且两者出现峰值的时刻点大致重合。模型计算值相对于实测值更为光滑,其原因是采用了简化的爆破荷载曲线。计算振速曲线7个波峰点处数值解和实测值的相对误差,得到1#测点的平均相对误差为13.4%,2#测点的平均相对误差值为9.1%,模型总体来说是可靠的。
2 计算结果分析
选取管道24个单元作为管道应力分析点,选取管道正上方A点、管道背爆侧B点以及迎爆侧C点作为模型振速分析计算点,通过提取各计算点的力学响应值分析隧道开挖变形及爆破作用下管道的力学响应特征,如图5所示。
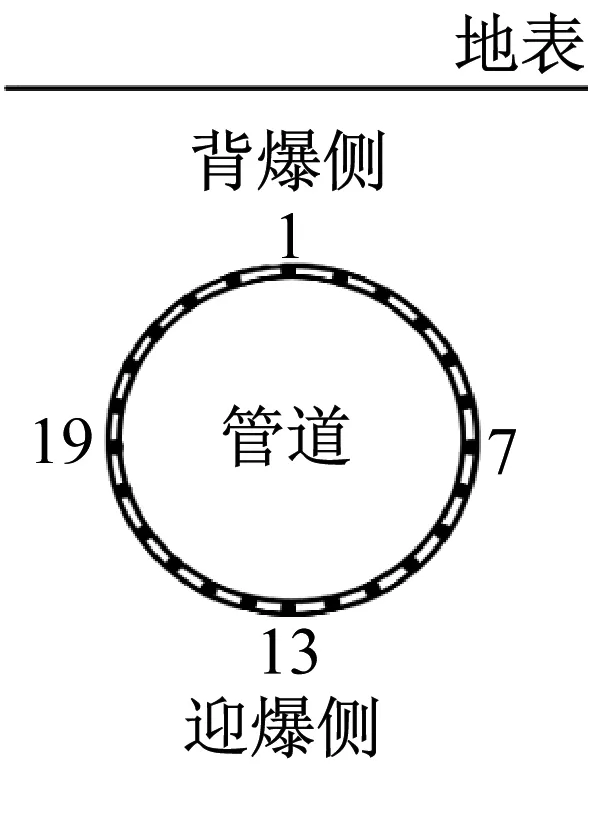
(a)
2.1 工况设置
实际问题中所涉及到的研究对象主要有管道、隧道、炸药以及岩土体,为综合考虑埋地管道的安全性影响因素,分别从这四者出发选取关键性的影响因素如下:管道内压、围岩弹模、管隧间距、单段最大装药量。具体工况设置如表4所示。
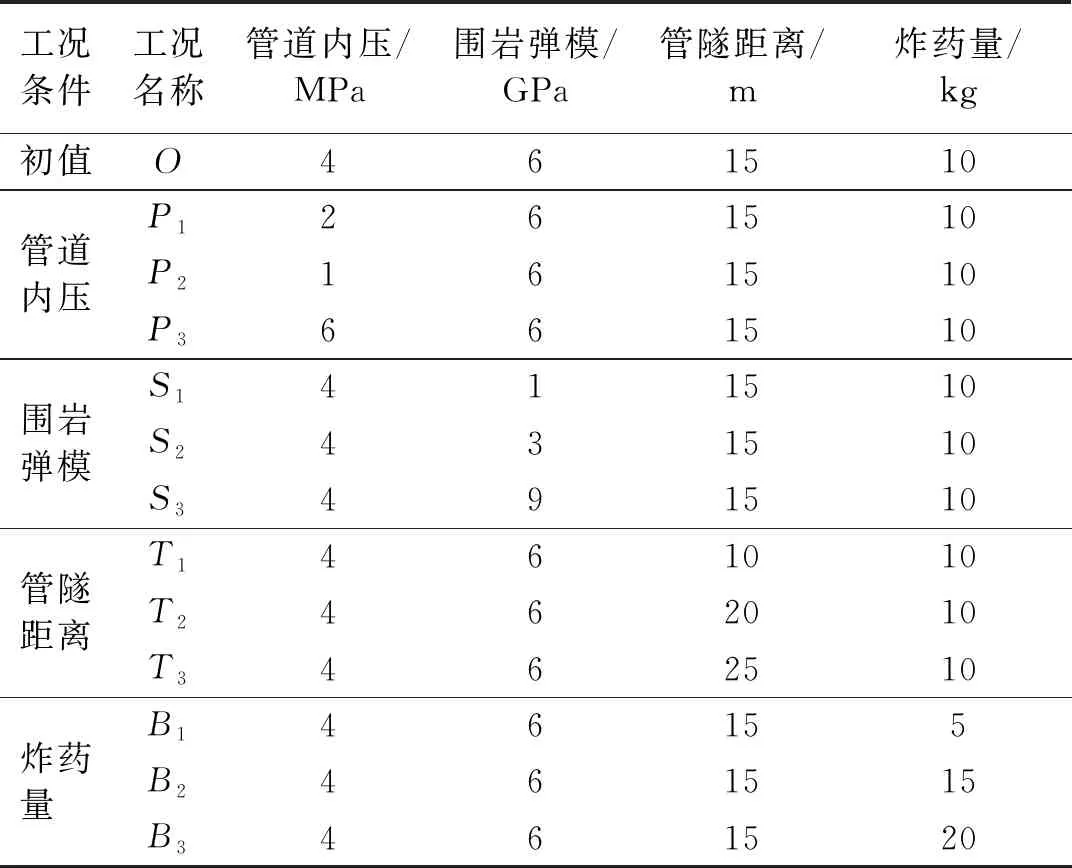
表4 计算工况表
2.2 管道内压的影响分析
为分析管道内压对管道安全性的影响,分别选取1 MPa,2 MPa,4 MPa和6 MPa 4种工况进行计算,具体工况设置如表5所示,不同内压下管道应力分布如图6所示。
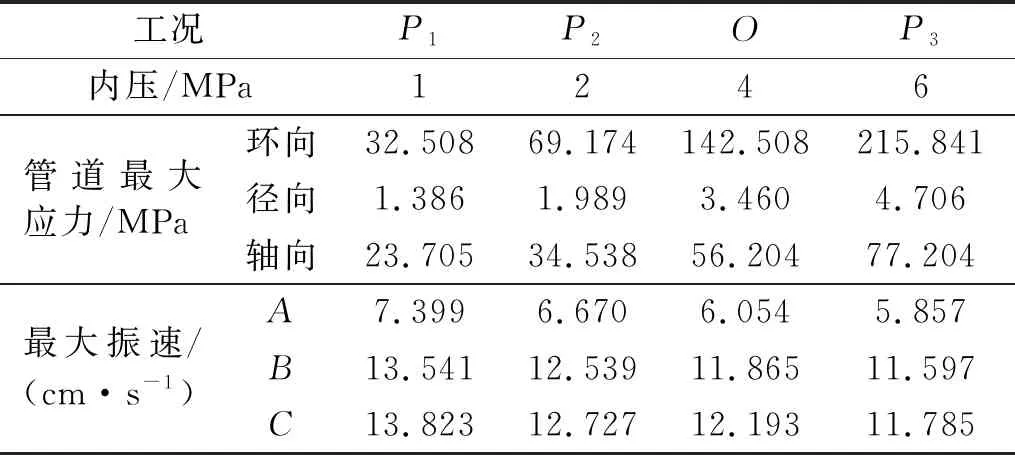
表5 不同内压下的管道应力及振速峰值统计表

(a) 管道径向应力
对比表5、图6可得:对于径向应力,拉应力峰值均位于管道两侧,其大小随内压增大而增大;随着内压的增大,管顶与管底由受压转为受拉,内压增大至4 MPa时,全环均受拉。对于环向应力,管道环向均受拉,应力峰值位于管顶和管底,其大小随内压增大而增大。对于轴向应力,管道轴向均受拉,最大应力位于管顶,最小应力位于管底,两者均随内压增大而增大。
管道内压对管道的应力状态影响较大,而对于管道振速的影响并不明显。各方向的峰值应力随着管道内压的增大呈近似线性增大趋势;而峰值振速不断减少。管道背爆侧B及管道正上方A的峰值振速与管道内压的关系为
(4)
2.3 围岩弹模的影响分析
为分析围岩弹模对管道安全性的影响,分别选取1 GPa,3 GPa,6 GPa和9 GPa 4种工况进行计算,具体工况设置参见表6。不同围岩弹模下的管道应力峰值分布如图7所示。

(a) 管道径向应力

表6 不同围岩弹模下的管道应力及振速峰值统计表
对于径向应力,拉应力峰值均位于管道两侧,其大小随弹模增大而增大;随着围岩弹模的增大,管顶和管底的应力值先增大后减少,当弹模为6 GPa时,管顶和管底出现压应力峰值。对于环向应力,管道环向均受拉,应力峰值位于管顶和管底;随着围岩弹模的增大,管道两侧的最小拉应力减小而管顶和管底的应力峰值增大。对于轴向应力,管道轴向均受拉;随着围岩弹模的增大,管底的应力先增加后减少而管顶的应力一直增大,应力图整体特征表现为从“中心分布”转向“偏心分布”。
管道背爆侧B及管道正上方A的峰值振速与围岩弹模的关系为
(5)
隧道围岩弹模增大,管道内壁各项应力指标均增大,但增大的幅度随之不断减小。分析其原因在于:随着围岩弹模的增大,一方面管道因开挖变形所产生的沉降减小,从而导致相应的附加应力减小;但另一方面爆破地震波的衰减趋势减弱,管道接收到的地震波能量增大,从而增大了管道应力,两者的耦合作用使得管道各项应力指标呈现出上述变化规律。
2.4 管隧间距的影响分析
为分析管隧间距对管道安全性的影响,分别选取10 m,15 m,20 m和25 m 4种工况进行计算,具体工况设置参见表7。不同管隧间距下的管道应力峰值分布如图8所示。
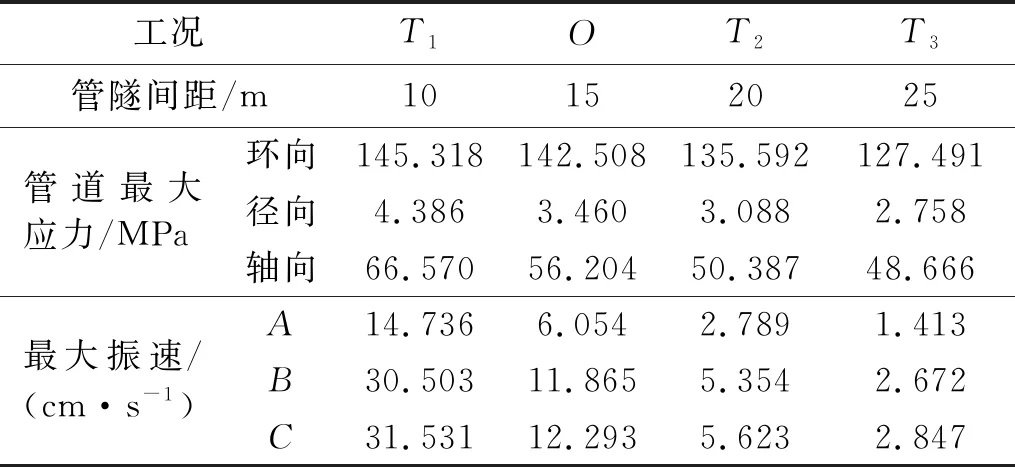
表7 不同管隧间距下的管道应力及振速峰值统计表
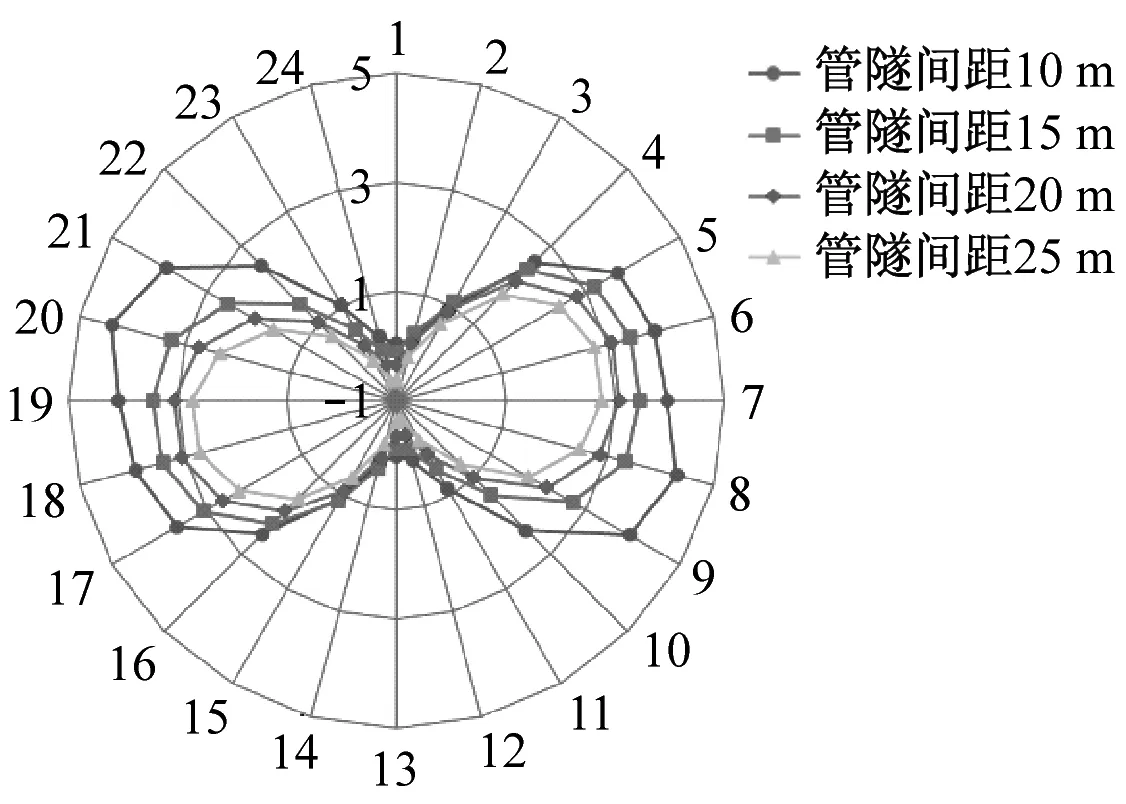
(a) 管道径向应力
对于径向应力,拉应力峰值均位于管道两侧,其大小随间距增大而减小;随着管隧间距的增大,管顶和管底的应力由拉应力转为压应力,在间距为15 m时,开始出现压应力。对于环向应力,拉应力峰值位于管顶和管底,其大小随间距增大而减小;当管隧间距减少至10 m时,在管道两侧一定范围内开始出现压应力。对于轴向应力,管道轴向均受拉;随着管隧间距的增大,管顶拉应力一直减小,而管底拉应力则一直增大,应力图整体特征表现为从“偏心分布”转向“中心分布”。
管道背爆侧B及管道正上方A的峰值振速与管隧间距的关系为
(6)
随着管隧间距的增大,管道的各项应力指标都呈现出减小的趋势,相应的应力峰值分布范围也会发生改变,而管隧间相对距离越近,爆破地震波能量的衰减程度越小,其对管道所产生的力学影响则越大,更易导致管道发生破坏。
2.5 爆破参数的影响分析
为分析爆破参数对管道安全性的影响,分别选取5 kg,10 kg,15 kg和20 kg 4种工况进行计算,具体工况设置参见表8。不同爆破参数下的管道应力峰值如图9所示。

表8 不同爆破参数下的管道应力及振速峰值统计表
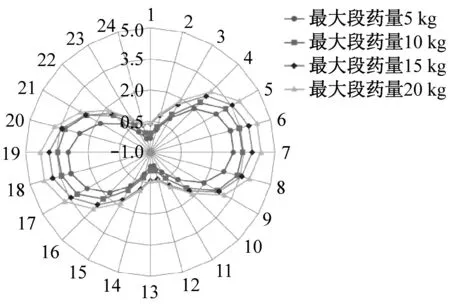
(a) 管道径向应力
对于径向应力,拉应力峰值均位于管道两侧,其大小随装药量增大而增大;随着装药量的增加,管顶和管底从受压转为受拉。对于环向应力,拉应力峰值位于管顶和管底,当最大单段装药量减少至5 kg时,管道两侧出现压应力。对于轴向应力,随着药量的增加,管顶拉应力值增大,管底拉应力值减小直至出现压应力,应力图整体特征表现为从“偏心分布”转向“中心分布”。
管道背爆侧B及管道正上方A的峰值振速与爆破参数的关系为
(7)
随着最大单段装药量的增大,管道各项应力指标都呈现非线性增大趋势,相对应的增幅也越大。对于工程控制而言,由于前述的管道内压、围岩弹模以及管隧间距等因素并不可控,故在实际施工中应将最大单段装药量作为保证管道安全性的一项重要参数。
2.6 参数敏感性分析
由以第2.1节~第2.5节分析可知,隧道开挖及爆破施工扰动下邻近管道的安全性主要受到管道内压、围岩弹模、管隧间距及最大段药量因素的影响。引入高颖会等[17]所采用的Morris筛选法对第2.1节~第2.5节影响管道安全性的参数进行局部灵敏度的检验,以确定各因素对管道安全性影响程度的大小。其计算公式为
ei=(Yi-Y0)/ΔXi
(8)
式中:ei为Morris系数,评价参数对研究对象的影响程度;Yi为参数变化后模型的输出值;Y0为参数变化前模型的初始输出值;ΔXi为参数Xi的变化量。
研究设置4种参数变量,改变参数值经过多次计算将模型所得到的平均变化率作为该参数的灵敏度,其计算公式为
(9)
式中:S为参数敏感性判别因子,即参数局部敏感度;n为每种参数变量对应下模型的运行次数。
根据参数的灵敏度值,可参数的敏感性分为4类,具体如表9所示。

表9 参数灵敏性分类
为确定管道内压、围岩弹模、管隧间距以及爆破最大单段装药量所对应的管道应力及管道峰值振速的敏感性,将表5~表8中的数据代入式(9)进行计算,整理后得到不同参数的Morris敏感度SN值如表10和表11所示。
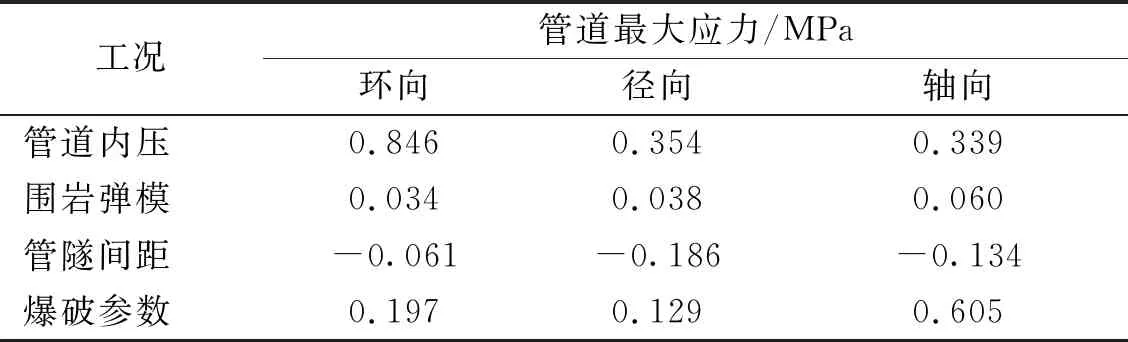
表10 管道最大应力的Morris敏感度表

表11 管道最大振速的Morris敏感度表
由表10和表11可知:
(1) 从管道应力角度分析,4种参数的影响程度由大到小依次为——管道内压、单段最大装药量、管隧间距、围岩弹模。其中,管道内压是管道环向应力、径向应力和轴向应力的敏感参数,对管道的应力控制起到关键性作用。而围岩弹模则是管道环向应力、径向应力的不敏感参数以及管道轴向应力的中等敏感参数。因此,在评估实际工程埋地管道安全性时,管道内压、爆破最大单段装药量以及管隧间距3项参数应在重点考虑范围之内。
(2) 从土体及管道质点的振速角度分析,4种参数的影响程度由高到低依次为——最大单段装药量、管隧间距、围岩弹模、管道内压。其中,最大单段装药量以及管隧间距均为土体及管道质点振速的敏感参数,而围岩弹模和管道内压则分别是土体及管道质点振速的中等敏感参数以及不敏感参数。因此,在评估实际工程埋地管道安全性时,应重点关注最大单段装药量以及管隧间距两项参数。
3 结 论
(1) 隧道开挖和爆破扰动耦合作用下,管道的径向应力峰值分布在管道两侧,环向应力峰值分布在管顶和管底,轴向应力峰值位于管顶,3个方向的应力峰值随着管道内压的增大、围岩弹模的增大、管隧间距的减小和单段装药量的增大而增大;远离拉应力峰值的区域,在各种参数的综合影响下,可能出现压应力。
(2) 引入Morris筛选法对影响管道安全性的参数进行了灵敏度检验,确定了4种参数对管道应力的影响程度从大到小依次为:管道内压、最大单段装药量、管隧间距、围岩弹模。对土体及管道质点振速的影响程度从大到小依次为:最大单段装药量、管隧间距、围岩弹模、管道内压。
(3) 管道底部迎爆侧的峰值振速略大于管道顶部背爆侧的峰值振速,其比值为1.02~1.07;而管道顶部背爆侧的峰值振速远大于其正上方土体质点的峰值振速,其比值为1.82~2.07。
(4) 实际工程中可通过控制装药量来控制管道的峰值振速,可通过降低管道内压以避免管道出现较大的拉应力。
