考虑时变啮合刚度的多惯量伺服系统机械谐振分析及抑制方法研究
2021-10-18李文礼刘永康石晓辉严海燕
李文礼, 陆 宇, 郭 栋, 刘永康, 石晓辉, 严海燕
(1. 重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;2. 东风汽车股份有限公司 东风商品研发院, 武汉 430056)
伺服系统是一种包括驱动电机、传动机构、负载和控制系统的典型复杂机电系统,其中传动机构的弹性使得系统本身存在谐振频率[1-3]。随着高性能伺服系统带宽的增加,当有谐振频率的信号作用到系统时,通常会使得系统发生机械谐振。这不仅会引起系统控制量振荡,影响系统的控制性能和精度;还可能会损坏传动机构、烧毁驱动电机。因此,对伺服系统机械谐振进行分析和抑制具有重要的意义。
为了抑制伺服系统的机械谐振,所使用的方法一般可分为两种,即主动抑制方法和被动抑制方法。主动抑制方法是国内外学者研究的热点,其原理是通过主动改变控制器参数或控制器结构来消除机械谐振,包括基于PI(proportional-integral control)的控制、基于模型预测控制(model predictive control,MPC)等高级控制算法、基于状态观测器的反馈控制等[3-10]。被动抑制方法主要是使用低通滤波器或陷波滤波器等来抑制机械谐振,但低通滤波器会带来相位滞后、陷波滤波器对系统参数变化较敏感等问题,容易导致系统动态性能变差[11]。杜仁慧等在考虑与机械谐振密切相关的系统参数不确定的情况下,基于反步法设计了自适应模糊控制器,有效地抑制了系统启动阶段和负载突变时的机械谐振。杨明等针对伺服系统中由弹性轴系引起的机械谐振及轴系安全性进行研究,在双惯量伺服系统模型基础上,对比分析了基于PI方法和MPC方法的不同控制效果,理论分析和仿真试验验证了MPC方法的优越性。Wang等[12]设计了动态表面控制与加速度反馈相结合的机械谐振抑制方法,利用高阶滑模加速度观测器来估计加速度信号,引入电机加速度反馈以减小机械谐振的影响。王建敏等[13]提出了一种双二次谐振抑制数字滤波器,能够将谐振点和反谐振点同时抑制。龚文全等[14]使用改进型陷波滤波器进行机械谐振抑制,以减小陷波器引入的相位滞后。
现有对伺服系统机械谐振分析及抑制问题的研究,多将伺服系统简化为双惯量模型,忽略了传动机构带来的影响,如传动间隙、齿轮啮合过程中时变啮合刚度等。但在实际工业应用中,传动环节存在不确定性,这意味着并不是所有情况都可以忽略传动机构的传动间隙、刚度、质量等参数[15-16]。为了更精确地抑制机械谐振和控制伺服系统,对多惯量伺服系统进行建模分析很有必要。相比于双惯量伺服系统,多惯量伺服系统模型复杂、谐振峰值不易理论推导,不适合使用被动抑制方法来抑制机械谐振。而基于MPC的主动抑制方法的预测方程不需要精确的数学模型,同时可处理各种带约束的线性、非线性问题,理论上可以很好的用于抑制多惯量伺服系统的机械谐振问题。基于上述分析,本文考虑时变啮合刚度对系统机械谐振的影响,首先建立四惯量伺服系统模型,并对系统的机械谐振产生机理进行分析。采用MPC方法对含时变啮合刚度的四惯量伺服系统机械谐振进行抑制,通过仿真验证了MPC控制器的有效性。
1 四惯量伺服系统模型及谐振分析
伺服系统在许多工业领域如数控机床、机器人、电动汽车驱动系统、高端试验装备以及国防工业中应用十分广泛,其转矩传递通常由多个不同的机械传动机构完成。如图1所示为一个典型的伺服系统结构,负载通过联轴器、齿轮箱、传动轴等与驱动电机相连。为了更精确地对系统机械谐振抑制进行研究,本文建立考虑时变啮合刚度的四惯量伺服系统模型。
1.1 四惯量伺服系统
为了便于分析,忽略图1中电机的电磁阻尼和电磁刚度、轮齿啮合综合误差,将电机、齿轮箱的主被动齿轮和负载简化为4个集中的转动惯量元件,建立如图2所示的四惯量伺服系统模型。该模型中电机转轴通过齿轮副与负载连接,系统输入为电机端电磁转矩Te直接作用于电机转轴,负载端传递转矩Ts2与负载转矩TL共同作用决定负载端输出转速,Ts1为电机转轴与齿轮1之间的传递转矩。
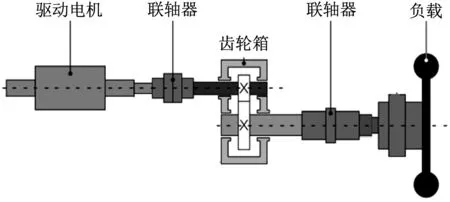
图1 伺服系统示意图
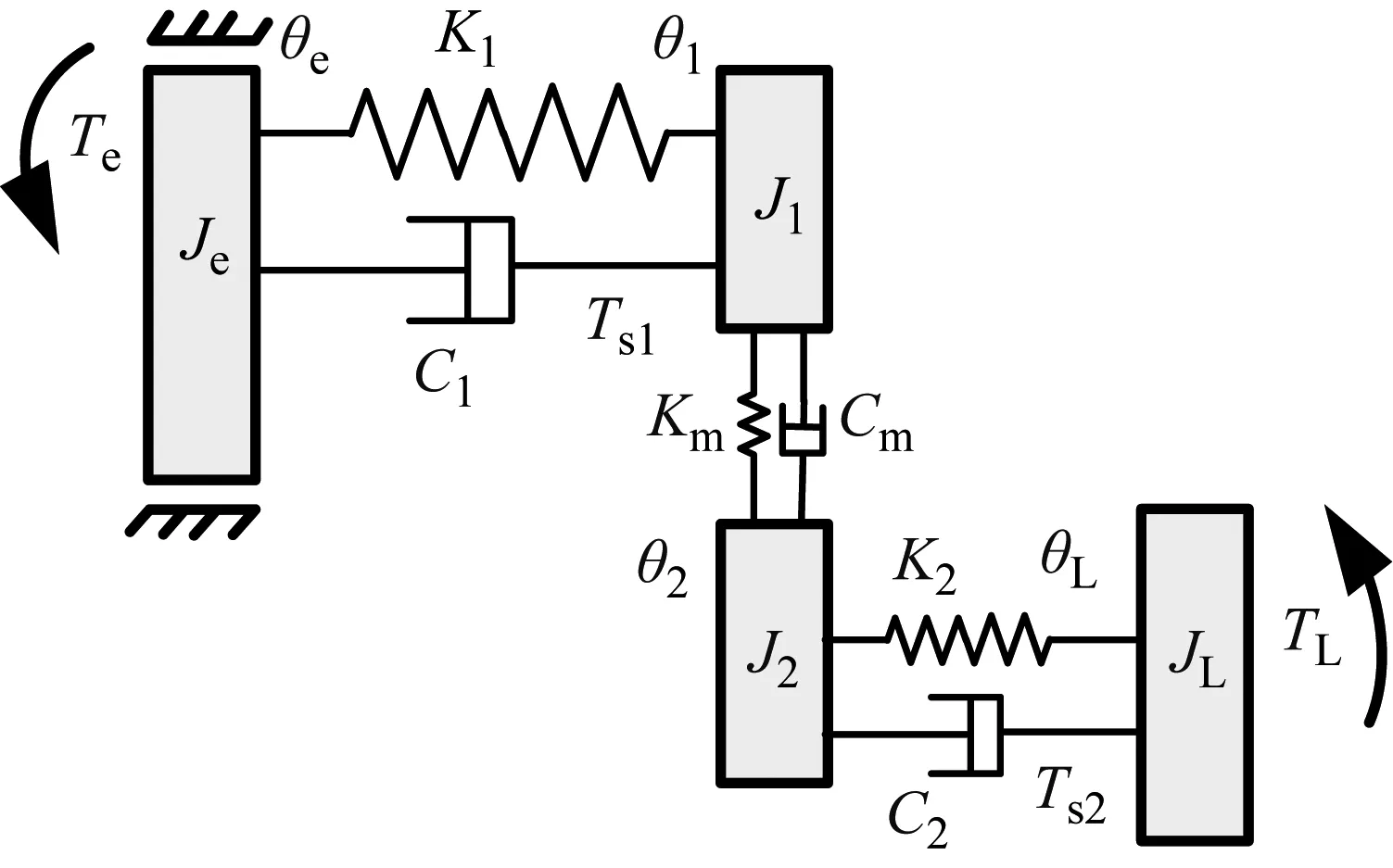
图2 四惯量伺服系统模型
图2所示的系统动力学方程可以表示为

(1)
式中:θe,θ1,θ2,θL分别为等效电机轴、齿轮1、齿轮2和负载的转角;Je,J1,J2,JL分别为电机、齿轮1、齿轮2和负载的转动惯量;Wd为轮齿的动态啮合力;Rb1,Rb2分别为齿轮1和齿轮2的基圆半径;C1,C2分别为输入轴与输出轴的阻尼系数;K1,K2分别为输入轴和输出轴的刚度系数;Cm,Km分别为齿轮副的啮合阻尼和啮合刚度。
1.2 机械谐振分析
在实际伺服系统中,机械传动机构由于不是理想刚体而表现出一定的弹性形变,弹性形变的存在会引起系统的机械谐振。将齿轮副的啮合刚度等效为一个定值(即啮合刚度为定刚度,这里取Km为5×107N/m)时,由式(1)可以得到所建立的四惯量伺服系统中输入量电磁转矩到输出量电机转速的波特图,如图3所示。
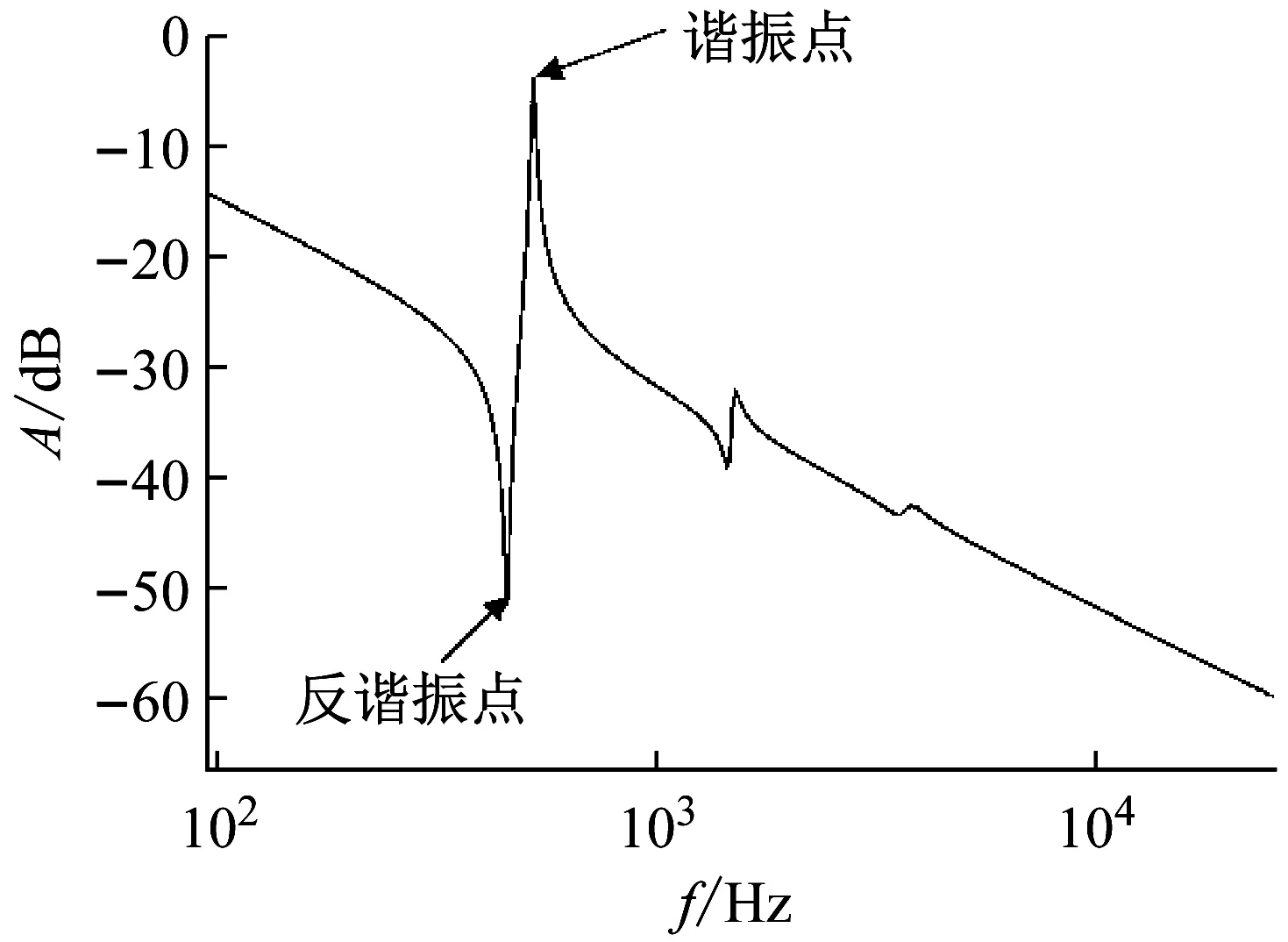
图3 电机端转速反馈时伺服系统波特图
从图3中可以看出,系统存在3对谐振点和反谐振点,即系统中输入轴、输出轴和齿轮副都将给系统带来共轭零极点,进而产生与其对应的机械谐振。因此,系统电机转速ωe和电磁转矩Te之间的传递函数可以简化表示为[17]
(2)
式中:ωbn和ωan分别为第n个谐振环节的谐振频率和反谐振频率;ξbn和ξan分别为第n个谐振环节的谐振阻尼系数和反谐振阻尼系数。
由式(2)可得给系统带来机械谐振环节的传递函数为
(3)
对式(3)分析可知系统的谐振频率与传动机构的刚度系数和系统各部分等效惯量有关。
为了研究系统负载端转速控制性能,假设啮合定刚度分别为5×107N/m,5×108N/m和5×109N/m,系统其余参数不变,可以得到如图4所示的不同啮合定刚度下四惯量伺服系统中输入电磁转矩到输出负载端转速的波特图。由图4可知,定刚度值的变化会改变系统的谐振频率,即系统谐振频率值会随着定刚度值的增加而增加。
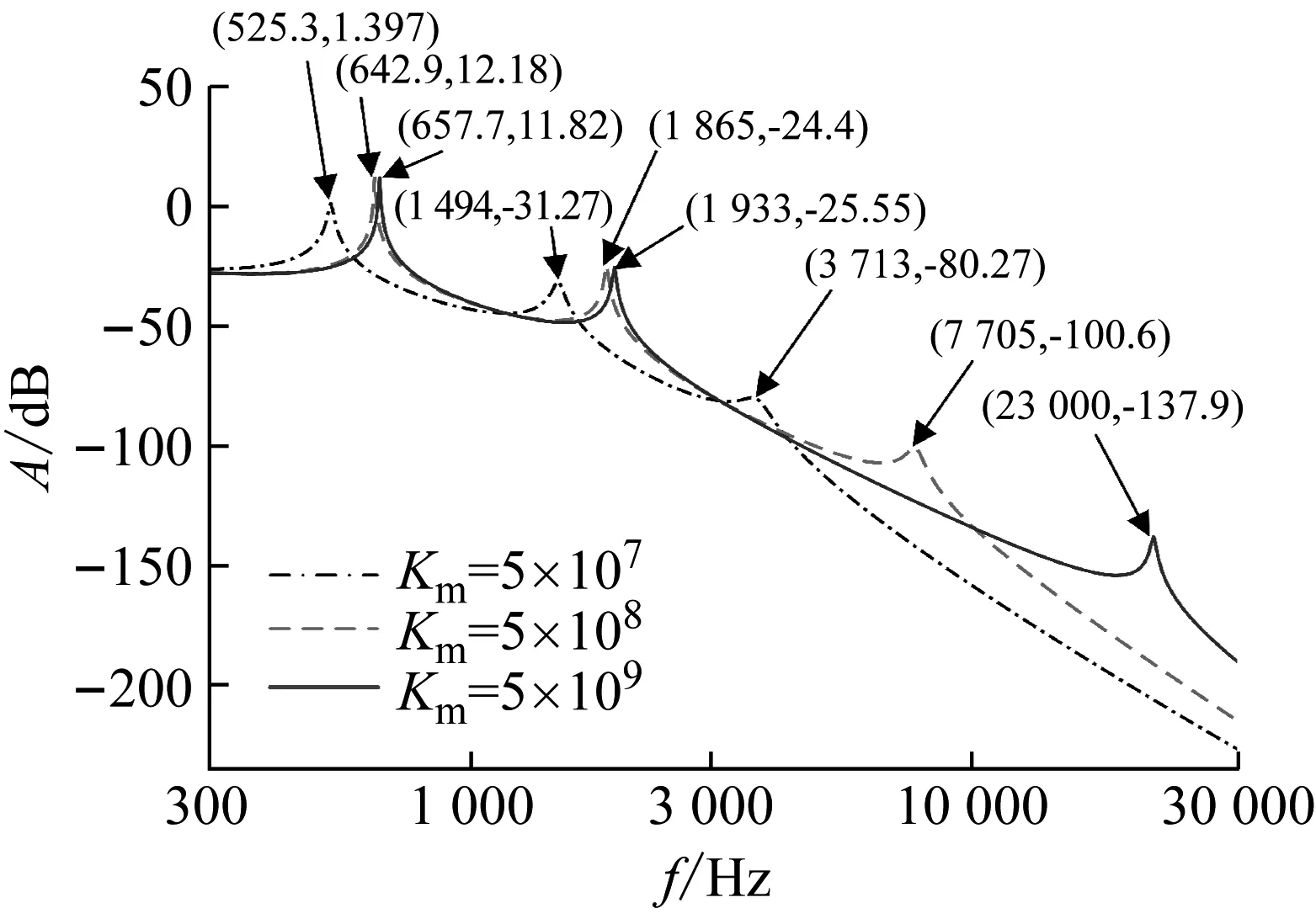
图4 负载端转速反馈时伺服系统的波特图
2 时变啮合刚度
齿轮副啮合刚度的变化会改变系统的谐振频率,从而对系统机械谐振产生影响。时变啮合刚度产生机理为在齿轮副啮合过程中,同时参与啮合的齿对数随时间而周期变化,从而导致啮合刚度随时间变化[18]。精确估计啮合刚度变化通常使用有限元法,但这种方法建立的模型很难加入到控制系统中。本文使用如图5所示的时变波形来近似表示啮合刚度值,以到达在控制系统中建模的目的。在每个啮合周期Tsc里,当齿轮为双齿啮合状态时,即(ε-1)Tsc时间段啮合刚度为最大值,ε为重合度;当齿轮为单齿啮合状态时,即(2-ε)Tsc时间段啮合刚度为最小值。
啮合周期可以表示为
(4)
式中:Z1,Z2分别为齿轮1和齿轮2的齿数;f1,f2分别为齿轮1和齿轮2的转动频率。
为了确保齿轮连续平稳的传递动力,重合度需大于1,其表达式为
(5)
式中:Ra1,Ra2分别为齿轮1和齿轮2的齿顶圆半径;a为齿轮1和齿轮2的标准中心距;α为压力角;m为齿轮模数。
假设轮齿之间的接触为赫兹接触,轮齿的表面可以是圆形或椭圆形[19]。则最小啮合刚度可计算为
(6)
式中:E为杨氏模量;W为齿宽;υ为泊松系数。
最大啮合刚度为
Kmax=2Kmin
(7)
因此,时变啮合刚度函数可以表示为
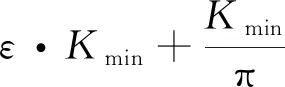
(8)
式中:λ=ε-1;ωsc=2π/Tsc。
根据本文选取的齿轮参数,如表1所示,求得重合度ε约为1.8,最小啮合刚度Kmin约为3.35×109N/m,λ为0.8;当转速为2 400 r/min时,输入轴转速频率为40 Hz,由于输入轴齿轮的齿数为20,齿轮的啮合频率为800 Hz,啮合周期Tsc为0.001 25 s。将上述值代入式(8)可以得到如图6所示的时变啮合刚度值,即时变啮合刚度最小值约为3.35×109N/m,最大值约为6.7×109N/m。

表1 伺服系统主要参数

图6 时变啮合刚度值
为了进一步探究时变啮合刚度对伺服系统机械谐振的影响,首先分析时变啮合刚度范围内谐振频率的变化范围,这里取啮合定刚度分别为时变啮合刚度的最小值、中间值和最大值的近似值,即3×109N/m, 5×109N/m和7×109N/m,系统其余参数不变,可以得到系统输入电磁转矩到输出负载端转速的波特图,如图7所示。由图7可以看出时变啮合刚度带来的机械谐振频率范围约为17 890~27 160 Hz。
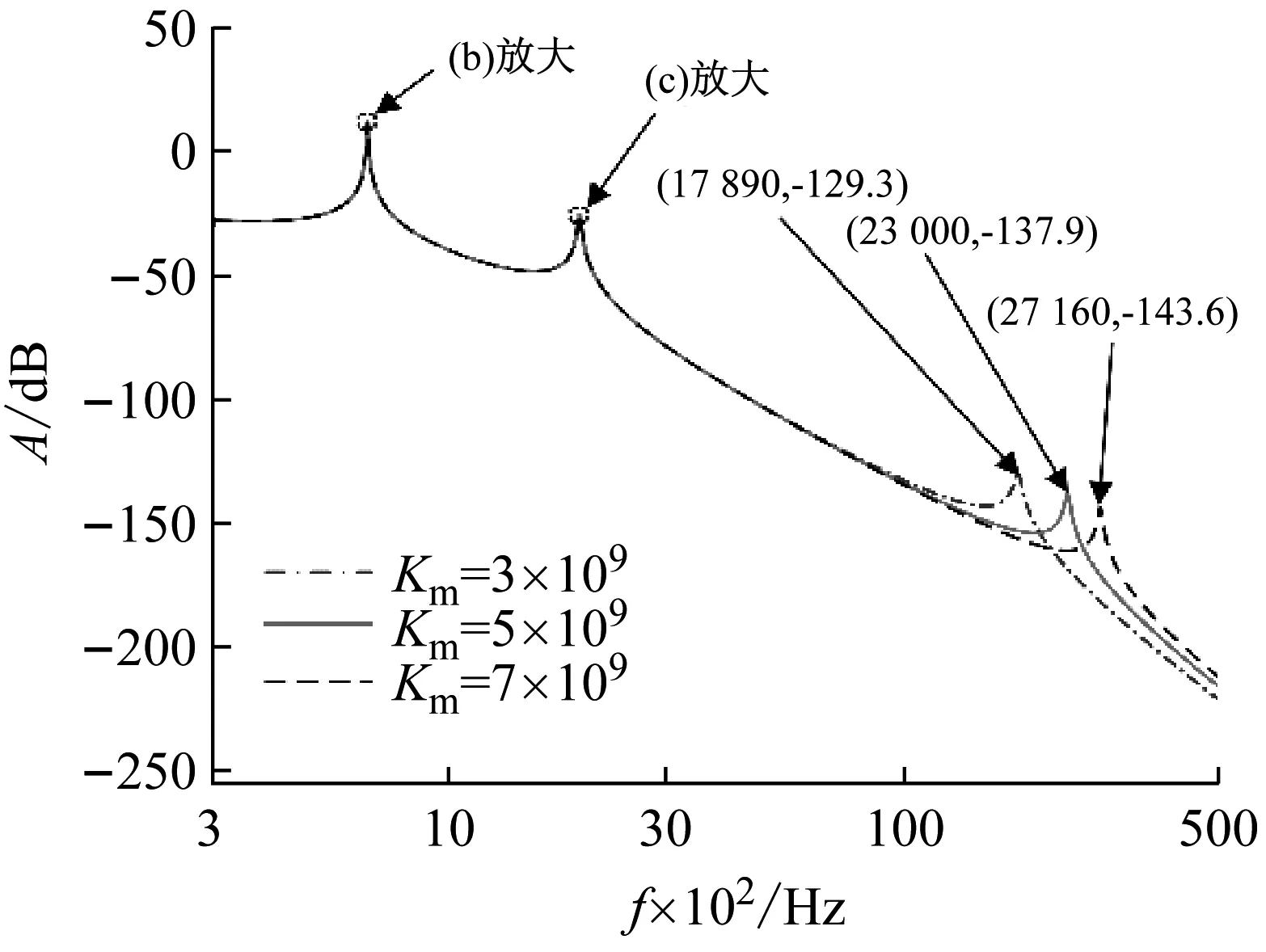
(a)
然后根据式(1)建立包含时变啮合刚度的四惯量伺服系统模型,对建立的伺服系统模型,对比分析其在啮合刚度为时变啮合刚度(即变刚度)和定刚度(Km为5×109N/m)情况下的机械谐振情况。当给定驱动电机为2 400 r/min的阶跃指令时,图8、图9分别为负载端传递转矩Ts2的时域波形和频域特性。由图8可知,在考虑变刚度参数时,系统传递转矩会产生更大的波动。图9为阶跃信号稳定后的频域特性,其中650 Hz和1 900 Hz附近产生谐振的是系统的输入轴和输出轴,23 100 Hz附近产生的谐振主要由齿轮副产生。可以看出变刚度系统中传动轴产生的谐振大于定刚度系统;定刚度系统在23 100 Hz产生较大的谐振,变刚度系统在23 100 Hz谐振不大,但以该频率为中心产生了两个较大的谐振带,且谐振频率间隔为800 Hz,这与图7分析的由时变啮合刚度引起的机械谐振频率范围基本相符。从定刚度和变刚度参数下系统的谐振情况对比可以看出,在对四惯量伺服系统机械谐振分析及抑制方法进行研究时,有必要将齿轮啮合刚度考虑为时变啮合刚度。
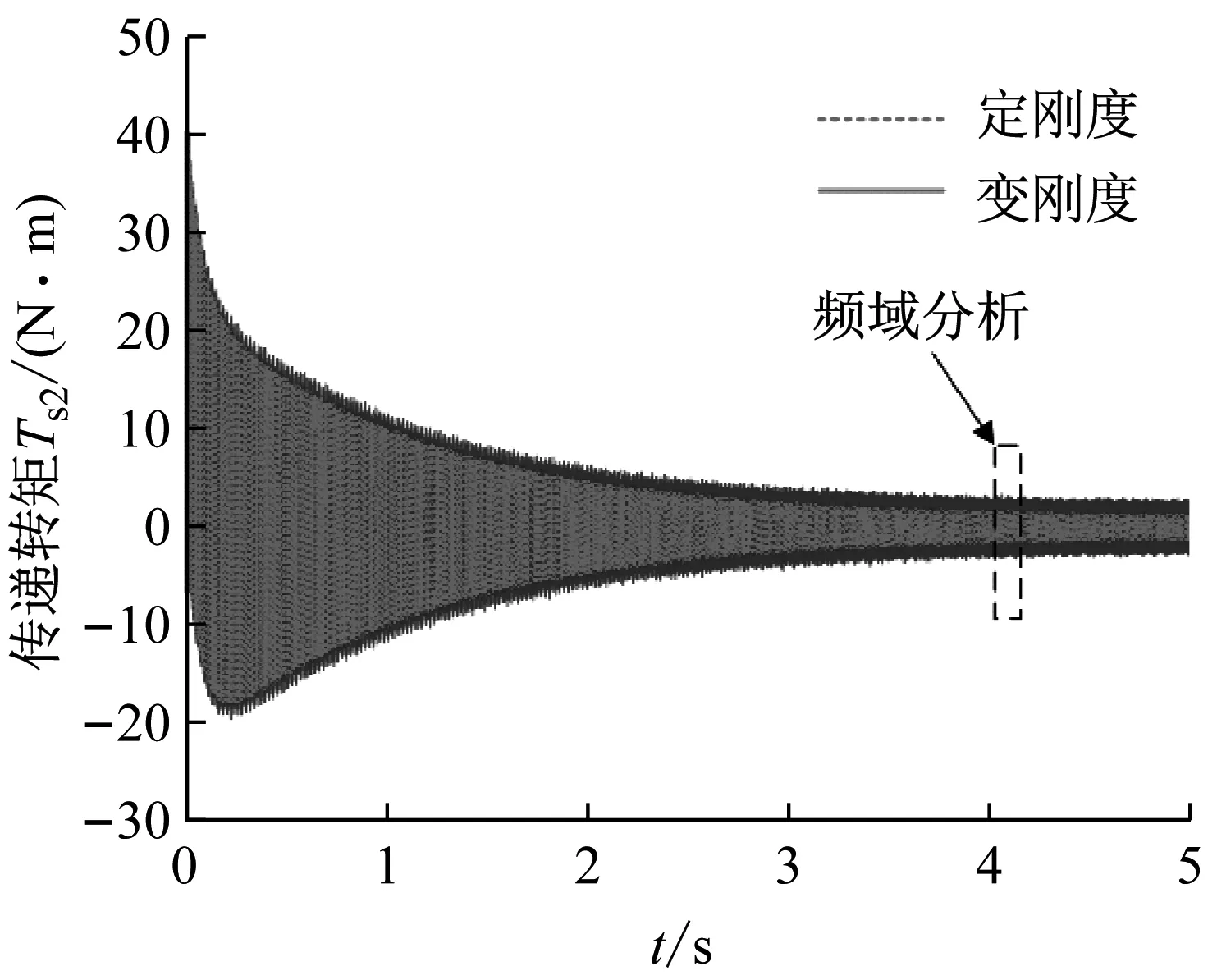
图8 定刚度和变刚度下伺服系统传递转矩Ts2变化

图9 定刚度和变刚度下伺服系统的频域特性
3 基于MPC方法的机械谐振抑制
MPC方法基本原理是根据系统的预测模型、当前时刻的状态和未来的控制量去预测系统未来一段时域的输出,通过滚动求解满足目标函数和各种约束的优化问题来得到系统实际控制输入量,从而实现控制目的[20]。为了对建立的包含时变啮合刚度的四惯量伺服系统机械谐振进行抑制,基于MPC方法获得系统控制输入量Te,控制的目标是有效地抑制系统的机械谐振,同时使系统具有良好的动态性能,即系统输出负载转速能很好地跟踪其参考值。如图10所示为伺服系统MPC控制框图,伺服系统处于速度控制模式。
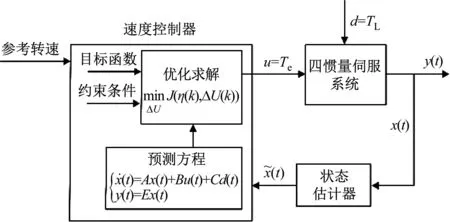
图10 伺服系统MPC控制框图
3.1 预测模型建立
考虑齿轮啮合刚度为时变啮合刚度,由式(1)可以得到四惯量伺服系统的连续系统状态空间方程

(9)


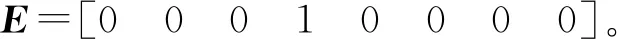
使用前向欧拉法对式(9)进行离散化处理,得到离散系统的状态空间方程为
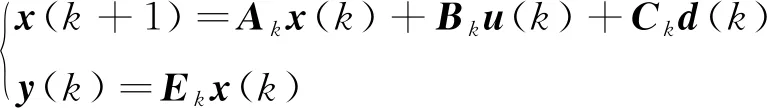
(10)
式中:k为当前采样时刻;k+1为下一个采样时刻。
3.2 目标函数设计
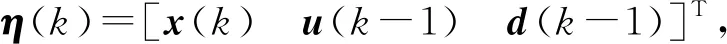
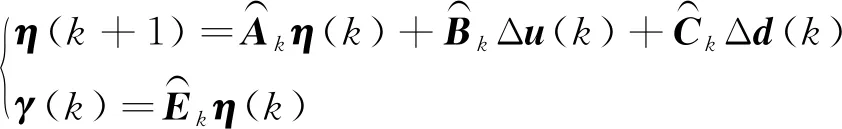
(11)
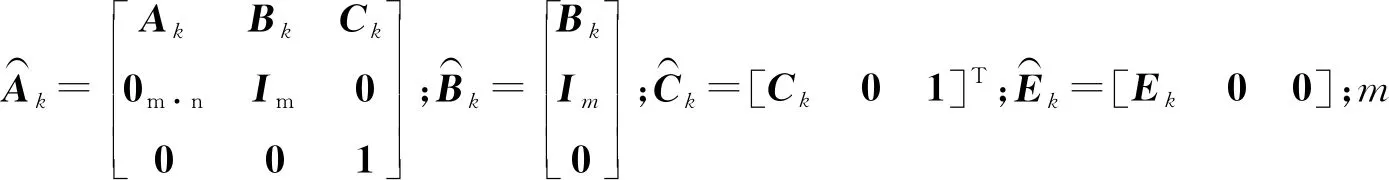
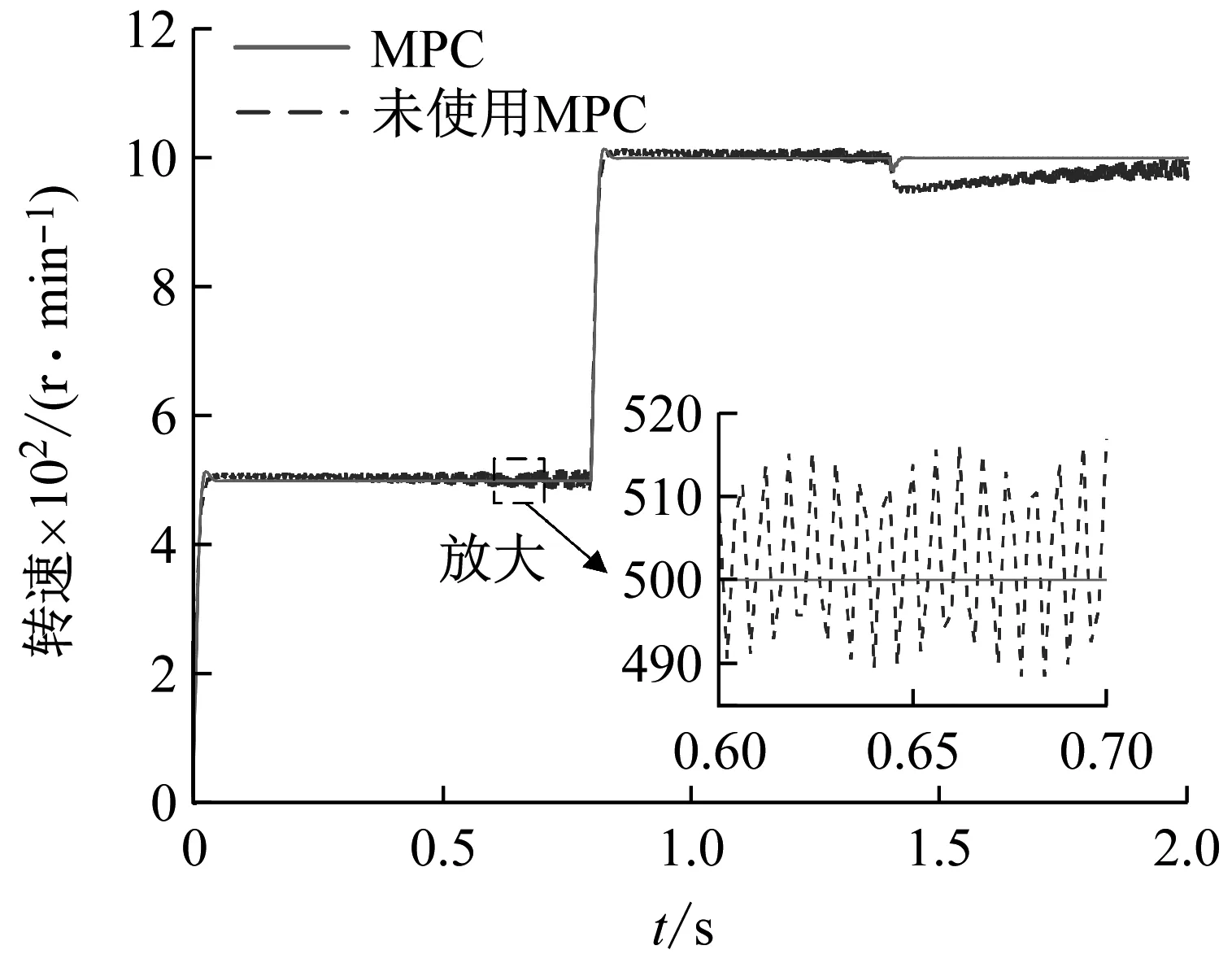
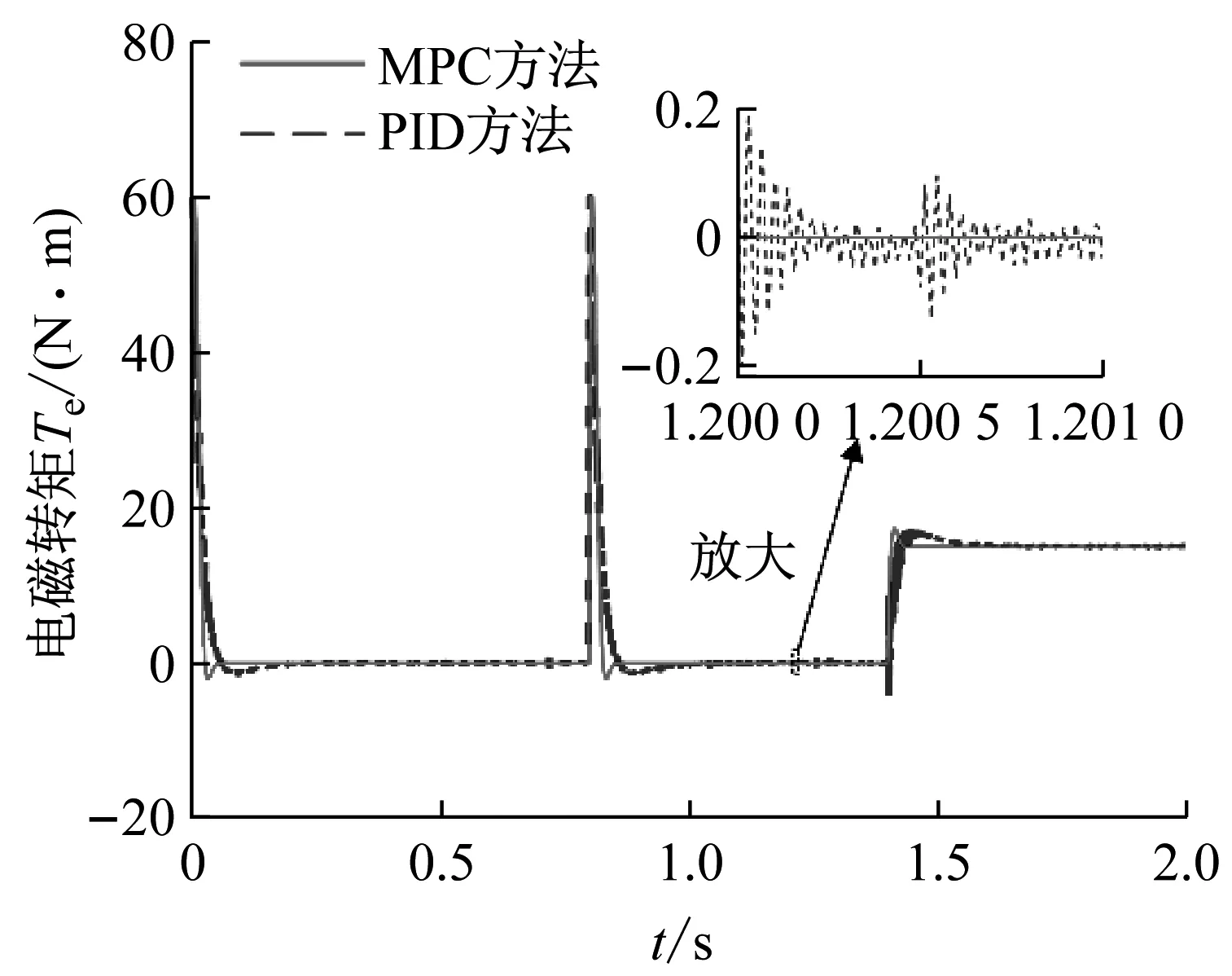
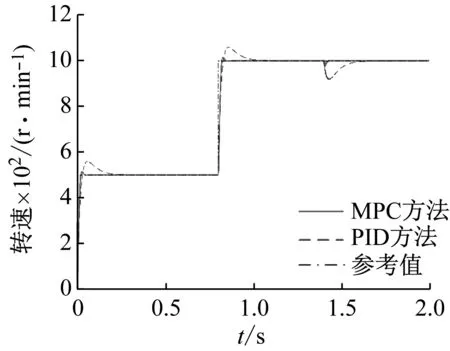
设定预测时域为Np,控制时域为Nc,Nc Y(k)=Φη(k)+ΨΔU+ΓΔD (12) 式中: 考虑系统控制目标为在不超过最大允许电磁转矩的前提下实现负载转速的精确跟踪,设计优化目标函数为 (13) 式中:Yref(k+i|k)为系统输出变量的参考值;(k+i|k)为以k时刻的系统输出量来预测k+i时刻的值,其中i=1,2,…,Np;ΔU(k+i)为k+i时刻系统控制输入增量,即电磁转矩增量,其中i=0,1,…,Nc-1;Q和R为权重矩阵。 系统需要对控制输入的电磁转矩、电磁转矩增量及系统输出施加约束条件,控制输入及其增量约束条件为 (14) 式中:umin和umax分别为电磁转矩的最小值和最大值;Δumin和Δumax分别为电磁转矩增量的最小值和最大值。 系统输出约束条件为 γmin≤γ(k+i)≤γmax (15) 式中,γmin和γmax分别为系统输出的最小值和最大值。 系统优化求解问题即在预测时域里,式(13)在满足式(14)、式(15)的约束条件下达到最小。即在每个控制周期里需要解决以下问题 (16) 通过求解二次规划问题,可以得到控制时域内的系统控制输入增量为 Nc-1)]T (17) 将控制输入增量的第一项Δu(k)取出,即可得到当前时刻系统控制输入为 u(k)=u(k-1)+Δu(k) (18) 为了验证MPC方法对包含时变啮合刚度的四惯量伺服系统的机械谐振抑制的有效性,并与基于PID方法的控制效果进行比较,在MATLAB/Simulink中建立了系统仿真模型。伺服系统主要参数,如表1所示。 MPC控制器主要参数设为:预测时域Np=20,控制时域Nc=4,权重取值Q=0.1,R=1,系统控制输入的电磁转矩范围|Te|≤60 N·m,系统输出的转速范围|γ|≤18 000/π r/min;PID控制器参数设为:比例系数1.35,积分系数20,微分系数0.001 5。仿真时转速阶跃响应参数设为:参考转速0~500~1 000 r/min,且在1.4 s突加30 N·m的负载转矩。 首先对使用MPC方法和未使用MPC方法(即速度控制器中为未经优化的PI控制)时负载端转速变化进行仿真对比,由图11转速阶跃响应可知,当伺服系统未使用MPC方法时,伺服系统负载端转速有很大的周期性振荡,这是由于系统中存在的机械谐振未被有效的抑制的原因。利用MPC方法能够减小负载端转速的振荡,即说明MPC能够抑制所建立的四惯量伺服系统的机械谐振。 图11 转速阶跃响应时负载端转速变化(有无使用MPC方法对比) 为进一步对比验证MPC方法的控制性能,利用MPC和PID控制方法对建立的四惯量伺服系统模型进行机械谐振抑制的仿真试验。图12为两种控制方法下系统控制输入的电磁转矩变化,使用MPC方法时控制输入的电磁转矩响应时间优于PID方法,且总体上振荡小于PID方法。图13为阶跃响应时负载端转速变化的仿真结果,可以看出MPC方法下的响应时间和超调量均优于PID方法,其中MPC控制下的超调量约为3%、PID控制下的超调量约为12%。加入负载转矩干扰后,MPC方法反应迅速,抗干扰能力好。图14和图15为阶跃响应下负载端传递转矩Ts2的变化曲线,由图14和15可知,在电机启动、加速以及负载转矩突变时,负载端传递转矩都有较大的振荡,使用PID方法时传递转矩的振荡大于MPC方法。仿真结果说明使用MPC方法抑制机械谐振的有效性且达到了预期控制效果。 图12 MPC和PID方法下转速阶跃响应时电磁转矩Te变化 图13 MPC和PID方法下转速阶跃响应时负载端转速变化 图14 MPC和PID方法下转速阶跃响应时传递转矩Ts2变化 图15 MPC和PID方法下转速阶跃响应时传递转矩Ts2变化(局部放大图) 机械谐振抑制对提高伺服系统的控制品质具有重要意义,本文为了更深入的研究多惯量伺服系统振动的机理、提高伺服系统的控制性能,主要做了以下工作。 (1) 考虑齿轮副时变啮合刚度对伺服系统机械谐振的影响,建立了由电机、主被动齿轮和负载组成的四惯量伺服系统模型,分析了系统机械谐振的产生机理,对比了有无齿轮时变啮合刚度的伺服系统模型机械谐振表现特征,以此说明考虑齿轮时变啮合刚度可使仿真模型更逼近真实系统。 (2) 基于包含齿轮时变啮合刚度的四惯量伺服系统模型设计了模型预测控制器,验证了MPC方法对考虑齿轮时变啮合刚度模型的谐振抑制的有效性,并与PID方法的控制性能进行了对比。 (3) 仿真结果表明,在转速阶跃响应中,MPC方法能有效抑制系统机械谐振的影响,其控制效果优于PID方法。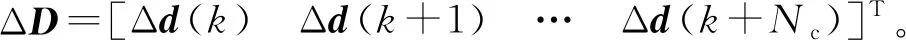
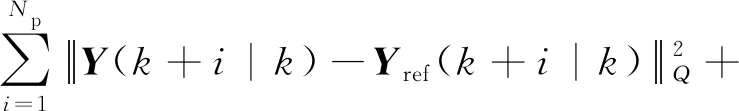
3.3 约束条件设计
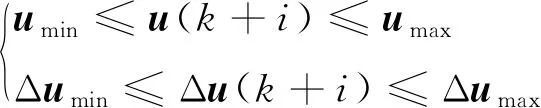
3.4 优化求解
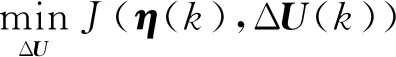
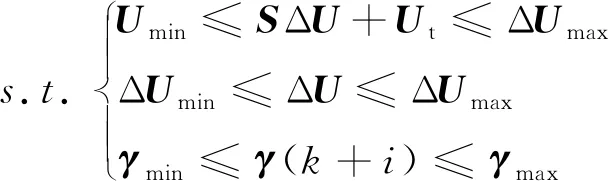


4 仿真及结果分析


5 结 论
