多卡箍支撑的管路系统振动特性半解析建模及支撑位置优化

刘旭东， 孙 伟

(1.东北大学 机械工程与自动化学院，沈阳 110819；2.东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819)

航空发动机外部管路是航空发动机的重要组成部分，主要用于燃油、液压油等介质输送。管路通过卡箍固定在机匣上，因而航空发动机的振动(主要是高压及低压转子系统引起的强迫振动)将通过机匣传到管路。当航空发动机的激振频率与管路系统的固有频率一致时会发生共振，使管路的振动幅度变大。过大的振动会使管路系统发生管体碰撞、管体裂纹、卡箍松动或断裂等振动故障，严重影响飞机的飞行安全。为了改善管路系统的振动性能，尤其是避开航空发动机的主要激振频率，必须对管路系统开展动力学优化设计，主要包括合理的设计管型以及优化布置卡箍的位置等。卡箍是通过箍带将管路固定，其必然会为管路系统提供支撑刚度及阻尼的作用，因而优化卡箍的位置(或布局)是避开共振和减少管路振动的一种最行之有效的方法[1]。

为了有效完成管路系统的避振优化，必须创建一个高精度的管路系统动力学分析模型。目前，完全以航空发动机管路为对象的动力学建模与分析的研究还不多见，但是以飞机、舰船和其他输送介质管路为对象或背景的管路动力学建模已有大量的研究，建模的方法包括传递矩阵法、有限元法及解析法等。例如Dai等[2]用传递矩阵法建立了3维输流管道模型并求解了管路系统的固有频率。Liu等[3]创建了包含14个频域方程的传递矩阵模型并分析了管路系统在弹性边界约束条件下的振动特性。Gao等[4]使用弹簧来模拟任意边界条件，并使用有限元法创建了一个简化的管道模型。Zhai等[5]使用有限元方法建立了铁木辛柯输流管道的动力学方程，并计算了管道的位移和速度。Kheiri等[6]应用哈密顿原理的扩展形式推导柔性支撑在悬臂管道末端的运动方程，实际上这是一种半解析法。同样Firouz-Abadi等[7]也利用扩展的哈密顿原理导出了悬臂管道的运动方程，然后通过Galerkin法进行离散化以获得管道系统的特征值。从上面评述可知，半解析法是一种常用的管路系统动力学建模的方法，本文也将利用半解析法完成多卡箍支撑的单管路系统动力学建模。不同于一般的双支撑梁结构，这种多卡箍支撑管路系统是一种超静定结构，因而对其进行半解析建模是一项挑战性的研究任务。

在各种管路系统动力学建模方法中，对支撑卡箍的力学特性的模拟是至关重要的。在大部分管路系统动力学建模中(包括前面所描述的各个文献)，卡箍一般采用弹簧-阻尼模型模拟，即，一个卡箍用一个线性弹簧和扭转弹簧外加阻尼模拟[8-9]。但是这种模拟方式有时并不能使管路动力学模型达到期望的分析精度，这主要在于卡箍支撑固定的是一小段管路而不是仅仅一个点。另外，卡箍对管路的刚度及阻尼作用还要受到螺栓预紧的影响[10]，因而参照Zhang等[11]的研究将模拟卡箍的分布弹簧设定为固定值可能是不恰当的。考虑到上述背景，本文提出用非均匀分布弹簧刚度值来模拟卡箍对管路的支撑刚度作用，以创建更加精确的管路系统动力学模型，进而提升卡箍布局优化的分析精度。

当前，围绕管路系统卡箍布局优化，研究者们已经开展了少量研究。Kwong等[12]使用遗传算法优化液压管道系统的卡箍位置，并得到了卡箍的最佳夹持位置。Herrmann等[13]在对管道系统动力学进行试验和数值研究的基础上，以减小噪声和振动为优化目标，对液压管道系统卡箍的夹持位置进行优化。Tang等[14]提出以累积疲劳损伤的失效概率最小为优化目标，通过合理设计管道系统中卡箍的位置来减少振动。为了提高航空液压管道系统的动力学性能，Li等[15]以系统阻抗的加权和为目标函数，采用混沌粒子群优化算法确定液压管道的最佳夹持位置。Zhang等[16]应用灵敏度分析法优化卡箍的位置。上述优化研究通常是以位移、应力等性能参数为优化目标来优化卡箍位置，最终实现管路系统的性能优化。还没有发现以航空发动机管路为研究对象或背景，以避开航空发动机高压、低压转子激振频率为目标的优化研究。但是，上述这些管路系统卡箍布局优化研究可作为本研究的重要参考。

本文以一个单管路多卡箍支撑的管路系统为对象，采用半解析法对其进行动力学建模。在建模时考虑到该系统是超静定结构，故本文提出先对管体建模再引入卡箍支撑力学特性的建模方法。接着，结合航空发动机管路避振设计标准建立卡箍布局的优化模型，并给出基于粒子群优化算法的求解过程。最后，用试验验证了半解析模型的合理性，并用粒子群算法对所提出卡箍布局优化模型进行优化，得到最优卡箍位置。

1 多卡箍支撑的管路系统半解析建模

本文将采用欧拉-伯努利梁理论和瑞利-里兹法完成对含多卡箍支撑的管路系统的半解析建模。由于这种多卡箍支撑的管路系统属于超静定结构，如图1所示，经典梁的建模方法并不适用本文研究。故这里将管体和卡箍分开建模，先对自由边界条件下的管体进行动力学建模，再将卡箍以弹簧形式引入整个系统进行动力学建模，以下简要描述相关建模过程。

图1 含多卡箍支撑的单管路系统

1.1 自由边界条件下管体建模

建立平面直角坐标系，首先考虑一个自由边界条件下的管体，管体长为l，外径和内径分别为D和d，如图2所示。这里仅考虑管体的横向位移w，即y方向的位移。

图2 自由边界条件下的管体

在任意的直管模型中，管体的横向位移w可表示为

w(x,t)=W(x)sin(ωt+φ)

(1)

式中:ω为管体的自由振动频率；W(x)为描述管体横向振动的模态函数;φ为初始时激励位移与管体位移的相位差。W(x)可以用一系列满足初始边界条件的特征正交多项式来描述，即

(2)

式中:n为实际计算时引入的多项式的项数；ai为对应多项式的系数；Ψi(x)为一系列特征多项式，可由Gram-Schmidt正交化求得。其具体求解步骤[17]如式(3)～式(6)所示。

(3)

式中，

(4)

对式(3)进行归一化处理

(5)

通过式(3)～式(5)可以求出一系列满足式(6)的特征正交多项式。

(6)

特征正交多项式的第一项φ1(x)需要满足初始边界条件。对于本文而言需要满足的边界条件是两端自由的边界条件。

在有了上述特征正交多项式后，基于欧拉-伯努利梁理论可知，管体的最大势能Umax和最大动能Tmax分别为

(7)

(8)

其中,

(9)

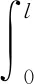
(10)

式中:E为管体的弹性模量；I为管体横截面惯性矩；ρ为管体密度；A为管体横截面面积。

自由边界条件下的能量方程为

J=Umax-Tmax

(11)

令

(12)

则自由边界条件下管体的动力学方程可表达为

(K-ω2M)a=0

(13)

式中：K为自由边界条件下管体的刚度矩阵；M为自由边界条件下管体的质量矩阵；a=[a1,a2,…,an]T为自由振动响应向量。

1.2 卡箍的支撑模拟

一个典型的卡箍-管体系统实物图，如图3所示。 从图3可知，卡箍通过环抱对管路起到固定作用，因而卡箍会对管路提供支撑刚度及阻尼的效应。为了简化建模大量的学者将这种刚度及阻尼效应用弹簧-阻尼来模拟。由于本文的目标是避振，因而相关的阻尼效应在本研究中被略去。

图3 卡箍-管体系统

图4 单管路多支撑简化模型

固定管路卡箍的局部放大图，如图5(a)所示。从图5(a)可知,卡箍是通过螺栓预紧将箍带固定在管路上，从而对管路起到支撑刚度的作用。前面已经提到用m个弹簧对来模拟卡箍对管路的支撑作用，由于螺栓预紧的不均匀现象，将这m个弹簧组的刚度赋予同一个值是不恰当的。为了更好的模拟被约束区域的受力状态，这里假定支撑区域弹簧的刚度值按正弦函数半个周期分布。其中：当m为奇数时，其分布如图5(b)所示；当m为偶数时，其分布如图5(c)所示。

(a)

在实际研究中，可通过反推辨识[18]获得相应的刚度值。由于支撑区的刚度被设定为按正弦函数半周期分布，因而最终的辨识只需获取一个刚度值。通常获取最大的刚度并通过计算获取其他弹簧的刚度值，具体计算式为

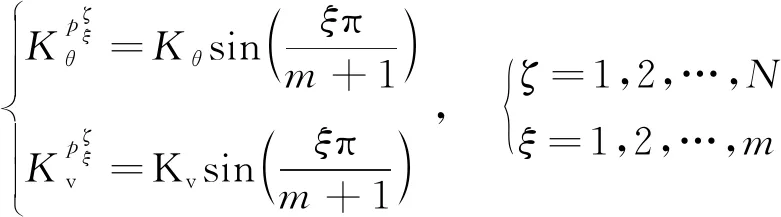
(14)

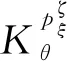
卡箍的刚度值具有分散性，通过直接静力学测试获得的刚度值可能与实际某一具体管路系统中卡箍的刚度值相差很大[19]，因而这里采用反推法确定卡箍的刚度[20]，其具体辨识原理，如图6所示。

图6 弹簧刚度辨识流程

这里的匹配计算采用遗传算法[21]进行刚度辨识。匹配计算中的目标函数可描述为

(15)

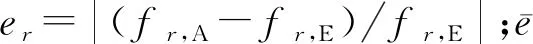
基于遗传算法进行刚度辨识时需要设置优化参数，首先需要设置最大迭代次数，种群大小即每一代中个体的数量(这里个体指线性弹簧刚度和扭转弹簧刚度)、二进制位数、交叉概率和变异概率。然后进行迭代计算，当满足最大迭代次数时，即可求得线性弹簧以及扭转弹簧的刚度值。

1.3 含多卡箍支撑管路系统的建模

考虑一对弹簧即一根线性弹簧和一根扭转弹簧所含有的能量，其能量可表示为

(16)

(17)

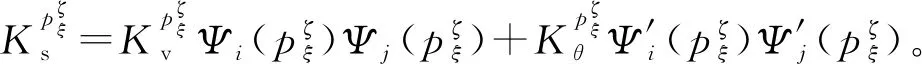
所有弹簧最大的能量可表示为

(18)

综合管体及各卡箍位置的能量，则含多卡箍支撑管路系统的能量方程为

Js=Us，max+Umax-Tmax

(19)

令

(20)

则含有多卡箍支撑的动力学方程可写为

(Ks+K-ω2M)a=0

(21)

式中，Ks为弹簧的刚度矩阵。

由式(20)即可求出含有多卡箍支撑的管体系统的固有频率及模态振型。

2 管路多卡箍支撑布局优化模型

为了完成通过优化卡箍位置实现管路系统有效避振的目标，必须创建合理的优化模型。创建该优化模型需考虑的各要素，包括卡箍位置、激振源和优化目标,如图7所示。其中卡箍的位置是设计变量，具体数值是以管路左侧端部为坐标原点进行计算的，图7中剖面线区域表示了卡箍的可达区域。激振源是对管路系统所处的激励环境的描述，可以是一个也可是多个。这里结合航空发动机运行的具体要求，以避开双激振源为优化目标开展研究。

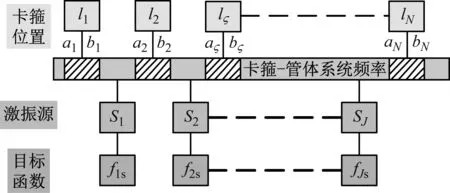
图7 卡箍位置与目标函数图解

实际上航空发动机中存在两个激振源频率:① 高压转子工作转速SH(以频率计);② 低压转子工作转速SL。一般情况下，在进行管路系统避振设计时应同时考虑发动机的两个激振频率，按照GJB 3816—1999《航空发动机管路系统通用技术要求》[22]，其设计要求可描述为

fr≥1.25SH或fr≤0.80SL

(22)

式中，fr为卡箍-管路系统的某阶固有频率。

由于航空发动机内部空间有限，可安装卡箍数量和位置也有限制。而卡箍的数量决定了卡箍-管路系统各阶频率的可变化范围，当管路系统的刚性不足时，管路系统的低阶频率可能落在危险区内，这里仅考虑第1阶及第2阶。按避振设计需要，需使管路系统第1阶、第2阶频率均落在安全区内，即第1阶频率f1<0.80SL，第2阶频率f2>1.25SH。以避开双激振源为优化目标的优化设计图解如图8所示。此时优化为多目标优化，其数学模型为

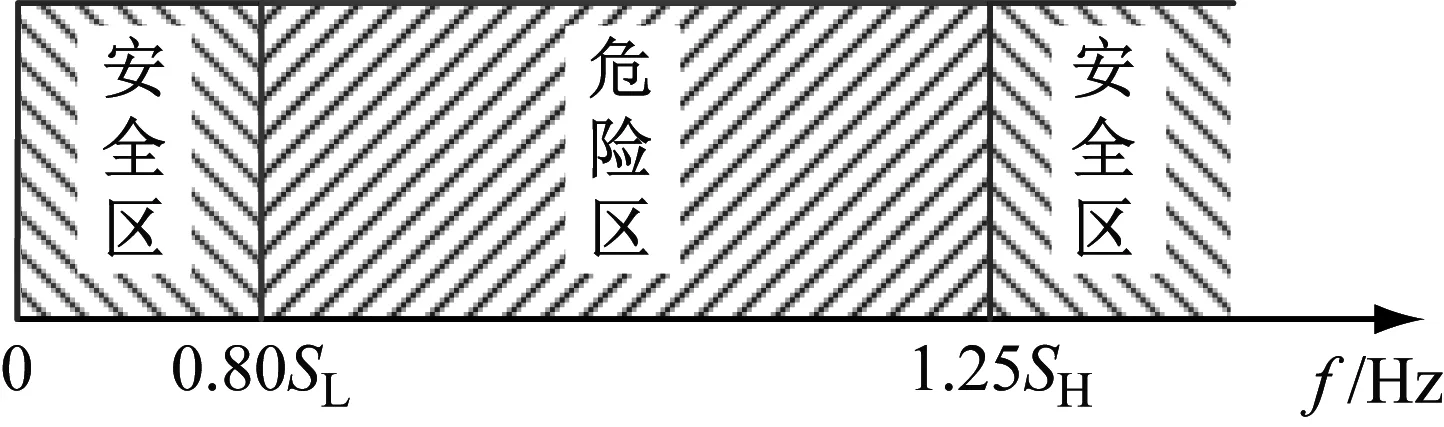
图8 避开双激振源优化设计图解

min -f1SL(l1,l2,…,lξ,…,lN,SL),

min -f2SH(l1,l2,…,lξ,…,lN,SH),

s.t.aξ≤lξ≤bξ，ξ=1,2,…,N,

f1-0.80SL≤0,

f2-1.25SH≥0

(23)

式中：f1SL为第1阶频率与低压转子工作频率的差值，f1SL=0.80SL-f1；f2SH为第2阶频率与高压转子工作频率的差值,f2SH=f2-1.25SH。

3 基于粒子群算法的优化模型求解

在创建完优化模型后，需要采用相应的优化算法求解支撑管路卡箍的最优位置，以达到避开激振频率的目的。这里采用粒子群算法对优化模型进行求解。

3.1 粒子群算法

粒子群算法[23-24]是一种随机的并行优化算法，其算法简单，并且可以很好的解决复杂的工程问题，针对本文的管路卡箍支撑布局优化具有很好的适用性。

粒子群算法在解决多目标问题有自身独特的优势。对于多目标优化问题，存在着多个彼此冲突的目标，一个解对于某个目标来说可能是较好的，但对于其他目标来说可能是较差的。因而就存在一个折中的集合称为Pareto最优解集。粒子群算法可以高效的并行地对非支配解进行搜索，每次迭代中都可产生多个非支配解。多目标粒子群算法优化出的结果是Pareto集，决策者可根据实际需要在Pareto集中选取优化结果。

3.2 卡箍布局优化求解

这里的优化问题是以避开双激振源为目标的多目标优化。以下描述采用粒子群算法求解上述优化问题的具体流程。

根据粒子群算法的特性，每一个粒子存在于D维空间，粒子中的每一个元素代表了一个决策变量(或设计变量)。对应于这里的卡箍布局优化问题，卡箍的数量是N个，因此粒子的维数也就是N维。

每个卡箍的位置的变化都会对卡箍-管路系统的固有频率产生影响，因而每个卡箍位置也就是一个决策变量。两者的对应关系，如图9所示。

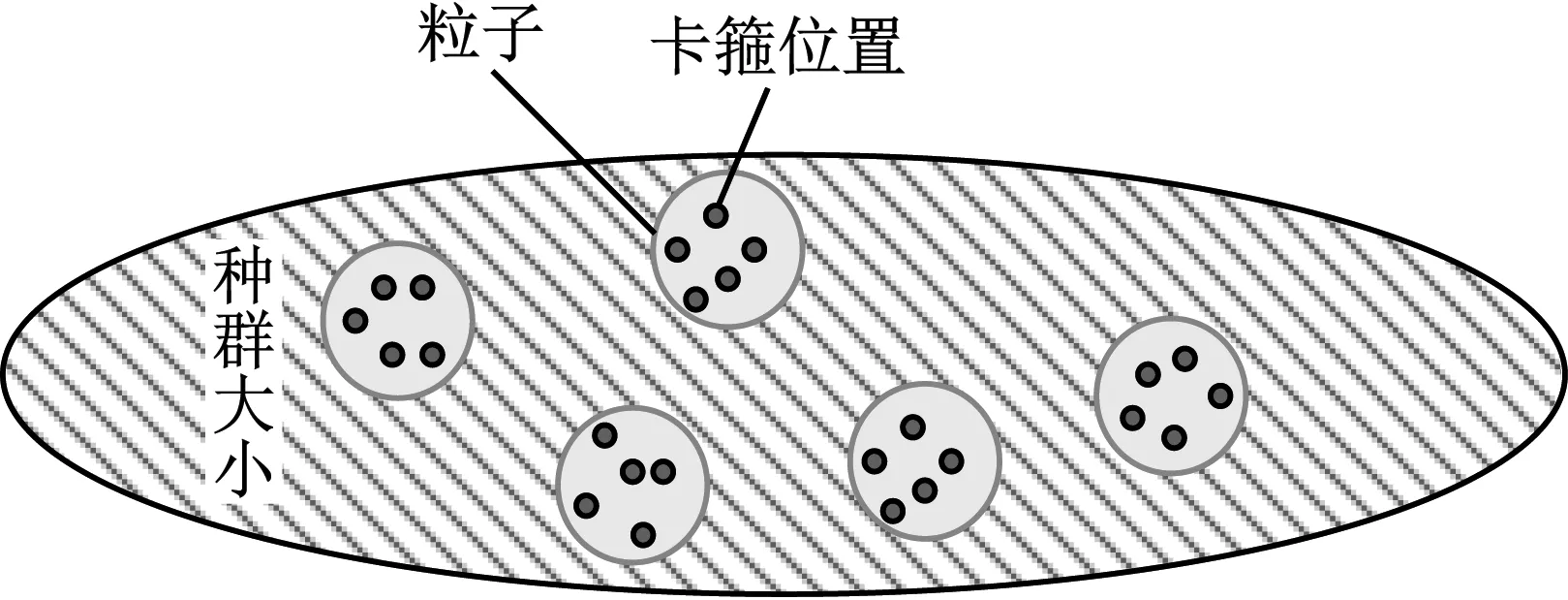
图9 粒子群决策变量图解

由M个粒子组成的种群，在第g代中各粒子位置和速度可表示为

(24)

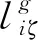
卡箍布局优化具体求解步骤如下。

步骤1初始化粒子群，群体规模为M，Pareto解集规模为M1。每个粒子的位置为li和速度为vi。

步骤2计算每一个粒子的适应度值-f1SL(i)和-f2SH(i),确定初始个体最优值pbest(i)和非支配解集Pareto。

步骤3更新粒子的速度vi和位置li，重新确定个体最优值pbest(i)。

步骤4对于每一个粒子，如果Pareto解的个数小于M1，则在新个体最优值pbest(i)中选取新的非支配解加入到Pareto解集中。否则先将拥挤度大的解删除再加到Pareto解集中。

步骤5判断算法是否满足迭代次数: 若是，则输出Pareto解集；否则返回步骤3。

4 实例研究

4.1 问题描述

以3个卡箍支撑的单管路系统为例展示所研发的管路系统建模以及以避振为目标的卡箍布局优化的方法。管路的几何参数如下:长L=500 mm，外径D=8 mm，内径d=6.4 mm，管体材料参数如表1所示。

表1 管体材料参数

首先，任意指定卡箍在管路系统的位置，如图10所示。以卡箍左端作为参考原点，3个卡箍分别置于l1=0.075 m，l2=0.250 m，l3=0.425 m处。3个卡箍的结构形状完全一致，每个卡箍的宽度为14 mm。管体通过卡箍中的螺栓固定在夹具上，螺栓拧紧力矩为4 N·m。由于本文研究的目标是避振，因而只需要测试管路系统的固有特性。这里采用锤击法对这个有3个卡箍支撑的管路系统进行模态测试，以获取管路系统的固有频率及模态振型，为研究方便只分析xy面内管路系统的弯曲振动。为完成管路系统模态测试，将管体等分为20份，共21个测点，用PCB SN 30272模态力锤在xy平面内依次敲击这21个测点，并用Polytec激光测振仪进行拾振。数据采集使用LMS SCADAS系统，试验结果通过LMS Impact Testing进行处理，最终可获得在此支撑工况下管路系统的固有频率及模态振型。这些模态数据主要用于校验所分析的模型，相关结果见后续的管路系统固有特性分析部分。

图10 卡箍-管路锤击试验

4.2 卡箍-管路系统固有特性求解

经研究，当多项式个数为20时已经能够达到所需精度。另考虑卡箍的宽度为14 mm，为了满足精度的要求，这里的m≥2。弹簧对数越多，则越接近于卡箍对管路的实际约束状态，但是过多的弹簧对数会导致计算效率下降，因而本文折中考虑取m=15。即采用15个线性弹簧和15个扭转弹簧模拟一个卡箍支撑。 其刚度值分布方式采用图5(b)的分布方式。根据式(14)算出3个卡箍中每一个线性弹簧和扭转弹簧的刚度值。以管路左端为坐标原点，由于卡箍的位置分别为l1=0.075 m，l2=0.250 m，l3=0.425 m，所以每个弹簧的位置也随之确定。根据式(1)～式(13)求出自由模态下的刚度矩阵和质量矩阵，然后按照式(16)～式(21)求出弹簧的刚度矩阵。最后采用遗传算法对弹簧的线性刚度和扭转刚度进行反推辨识，设置最大迭代次数为100次，个体数量为50，二进制位数为100，交叉概率为0.7，变异概率为0.01。反推辨识后线性弹簧的刚度值为Kv=4.258×105N/m和扭转弹簧的刚度值Kθ=86.5 N·m/rad。将得到得线性弹簧刚度值与扭转弹簧刚度值代回到半解析模型中计算固有频率。理论模型和试验的结果如表2和图11所示。

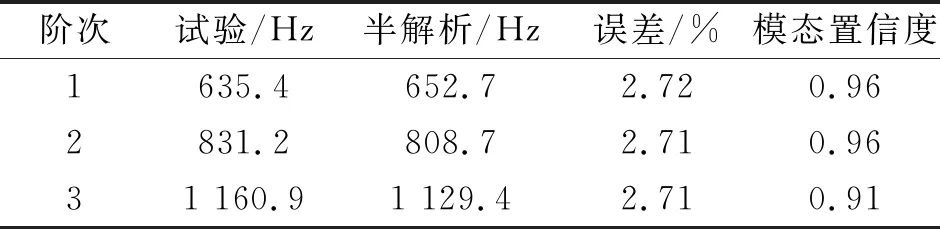
表2 卡箍-管体系统频率对比

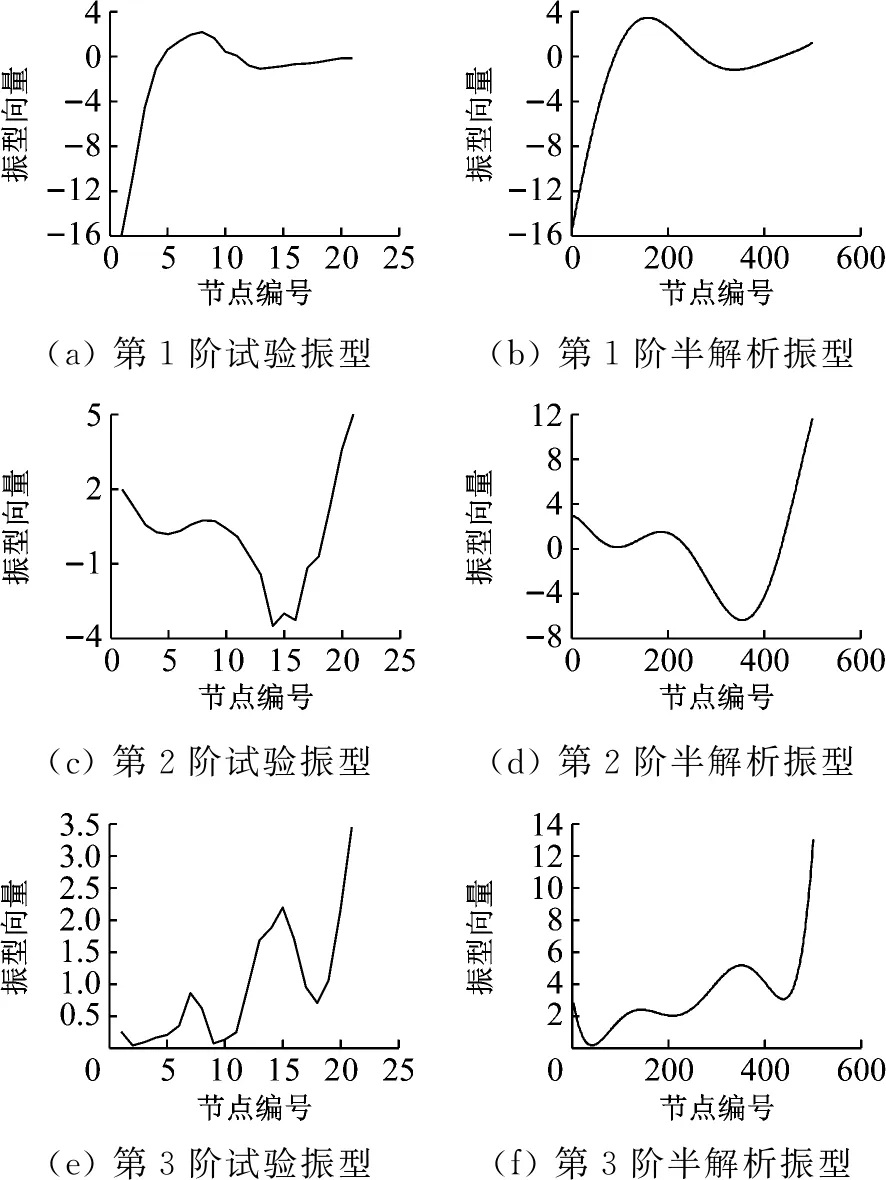
图11 半解析法与试验模态振型对比

需要说明的是，表2及图11中虽然是用反推法确定的卡箍刚度值又回代到管路系统半解析模型得到的结果，但是反推辨识需要基于正确的理论分析模型，这里得到：前3阶固有频率最大差值为2.72%，模态置信度最小值为0.91，这些数据客观上也能说明所研发的半解析模型的合理性。

4.3 卡箍布局优化

以避开双激振源为优化目标，将4.2节中计算的卡箍刚度值结合位置坐标以参数形式应用到粒子群算法中。设定高压转子频率为SH=580 Hz，低压转子频率为SL=400 Hz。种群大小设置为250，Pareto解集大小设置为200，迭代次数为200，学习因子c1=2.0，c2=2.5，惯性权重w=0.5。目标函数分别为-f1SL(l1,l2,l3,SL)和-f2SH(l1,l2,l3,SH)，卡箍位置约束条件为a1=0.002，b1=0.150，a2=0.170，b2=0.316，a3=0.336，b3=0.484。经过多次优化测试，当设置迭代次数为200次时，均能得到收敛结果，且每次优化只需800 s。其优化结果如图12所示。图12中圆点为Pareto解集，从图12可知，Pareto解均匀分布。当需要第2阶频率较小时可以选择点1此时优化结果f1=227.83 Hz，f2=957.30 Hz，对应的卡箍位置为l1=0.150 m，l2=0.316 m，l3=0.484 m。当需要第2阶频率较大时可以选择点2，此时优化结果为f1=229.59 Hz，f2=1 173.50 Hz，对应的卡箍位置为，l1=0.045 m，l2=0.186 m，l3=0.336 m。总之，在实际管路系统支撑优化设计时，决策者可以根据实际需要从优化解集中选取最优结果。

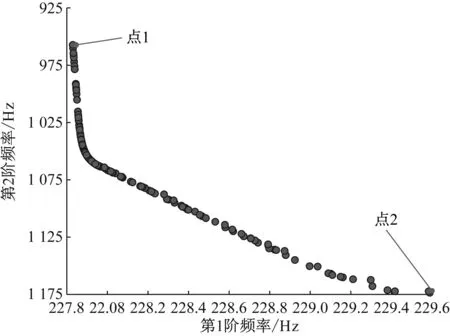
图12 以避开双激振源为目标的优化结果

4.4 优化结果验证

为了验证模型的合理性和优化结果的有效性，本文选取了点1和点2的优化结果所对应的卡箍位置分别作为试验的卡箍布局方案1和方案2。同时随机选取了两个非优化结果的卡箍位置做为卡箍布局方案3和方案4。将卡箍布局方案3和方案4作为对照用以验证优化结果的有效性。选取的卡箍布局方案如表3和图13所示。

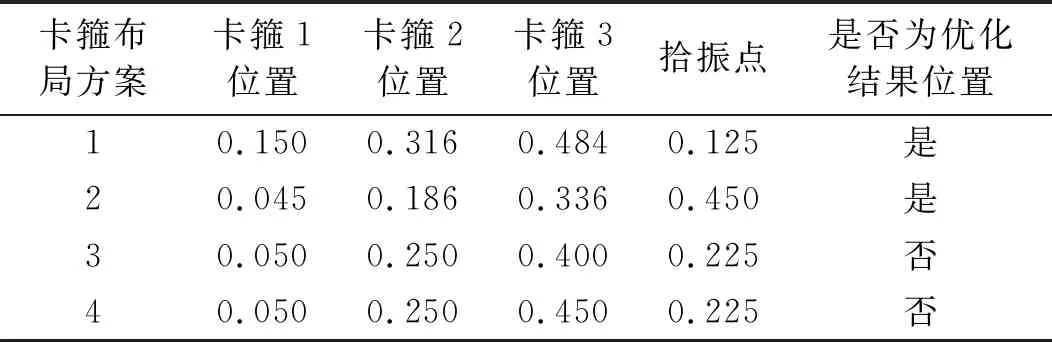
表3 卡箍布局方案

(a) 方案1

用PCB SN 30272模态力锤在xy平面内敲击管体，并用Polytec激光测振仪进行测量。数据采集使用LMS SCADAS系统，试验结果通过LMS Impact Testing进行处理。最终获得上述卡箍布局方案的频率结果，并将试验结果与仿真结果进行对比。其结果如表4所示。

表4 试验频率与半解析频率对比

从表4可知，4种卡箍布局方案的试验频率与半解析法算出的频率的误差最大为4.35%，进一步验证了本文半解析模型的合理性。优化位置的卡箍布局方案均符合避振设计准则，而非优化位置的卡箍布局方案的前2阶频率均在共振区，从而验证了本文优化结果的合理性。

5 结 论

对于航空发动机管路系统在动力学设计阶段避开共振是至关重要的，本文以单管路多支撑系统为对象，提出了基于粒子群优化算法实现卡箍优化布局进而实现有效避振的方法。得出如下结论:

(1) 这里提出将管体和卡箍分开建模来解决多卡箍支撑的超静定管路建模问题。先对自由边界条件下的管体建模，再将卡箍以弹簧的形式引入管路系统。在建模过程中，重点考虑了螺栓预紧箍带对管路系统刚度的影响，提出用非均匀分布(具体是正弦函数的半个周期)弹簧对来模拟卡箍的支撑。实例表明: 分析获得的固有频率与实测值相比偏差小于2.12%，而分析获得的振型与实测值的模态置信度大于等于0.92，从而证明这种建模方法可有效模拟管路系统的动力学特性。

(2) 航空发动机外部管路系统的激振频率主要来源于高压及低压转子的振动频率。本文以避开双激振源为优化目标，以卡箍位置为设计变量，创建了合适的优化模型。在该优化模型中，所描述的避振目标完全来自于行业规范，因而可对航空发动机实际管路设计起到一定的指导作用。

(3) 粒子群算法作为一种随机的并行优化算法，可以很好的解决本文描述的以避振为目标的卡箍布局优化问题。这里粒子中每个元素描述了卡箍的位置，实例计算表明，该优化算法可以快速收敛，从而找到可以有效避开共振的管路系统中卡箍的最优位置。