基于自动编码器和长短时记忆网络的智能汽车故障诊断方法研究

闵海根， 方煜坤， 吴 霞， 王武祺， 宋晓鹏

(1.长安大学信息工程学院， 西安 710064；2.长安大学“车联网”教育部中国移动联合实验室， 西安 710064；3.浙江省交通规划设计研究院有限公司， 杭州 310017)

1 引 言

近年来，具有自动驾驶和网联功能的智能汽车受到越来越多的关注，与之相关的技术有望大幅提升交通效率[1-2].智能汽车的安全性问题是目前阻碍其大规模落地的重要因素之一，因而故障诊断技术对于保证智能汽车安全行驶必不可少.故障诊断能对系统发生的故障进行有效检测、识别，并采取一定补救措施，保证系统稳定.Gao等[3-4]对现有的故障诊断算法进行了系统地总结，将这些算法大体分为三类：基于模型的方法，基于特征信号的方法和数据驱动的方法.(1) 基于模型的方法首先对被研究对象进行建模[5]，通过检测模型输出和系统实际输出之间的一致性判断系统是否异常.在故障诊断领域，卡尔曼滤波[6]是一种广泛应用的基于模型的方法，通过对研究对象进行建模，利用卡尔曼滤波对系统当前时刻状态进行估计，比较估计值和量测值之间的差异，从而判断系统是否异常;(2) 基于特征信号的方法假定系统状态可以被特定的信号所反映，监测这些信号并结合对系统的先验知识对系统是否异常做出判断;(3) 数据驱动的方法则通过对大量系统历史数据的挖掘，学习系统的部分特征，在进行故障诊断时，这类方法通过比较当下采集的特征和学习到的特征之间的差异性，对系统是否异常做出判断.

对于智能汽车的各个子系统，获取相关的先验知识或者对其精确建模通常比较困难，因而利用数据驱动的方法对系统进行故障诊断受到了更多的关注.针对故障诊断任务，异常数据往往难以获得，这使得无监督学习方法在故障诊断任务中得到关注.无监督故障诊断的基本思想是[7]：训练数据全部为正常数据或者含有少量故障数据，设计机器学习算法，学习研究对象的某些特征表示.由于训练数据中正常数据占据主导地位，学习到的特征表示就表征了正常情况下系统的特征.待检测样本的这些特征表示如果和学习到的特征表示存在较大差异，则认为存在异常.根据数据的不同特点，两类常见的方法分别是基于重构的方法和基于预测的方法.基于重构的方法首先将数据压缩到特征空间，再将数据进行重构，其基本假设是[7]：正常数据可以被较好地从特征空间重构，异常数据则不能.如果重构的数据和实际测量数据差异过大(即重构误差过大)，则认为存在异常.自动编码器(Autoencoder， AE)[8]是这类方法的典型，训练阶段，编码器将训练数据映射到特征空间，学习研究对象的特征表示，再利用解码器重构数据；测试阶段，那些不能被很好重构的数据点被认为是异常.这类方法对时间关联性较弱的数据通常性能较好，但是无法处理时序数据.时序数据的特点在于数据之间存在时间关联性，遵循着某种时间上的依赖关系.基于预测的方法就是要学习时序数据的时间关联性以及数据之间在时间上的依赖关系，其基本假设为[7]：一旦模型学习到研究对象的时间依赖关系，正常数据将可以被准确地预测，异常数据则不能.如果预测的数据和实际测量数据差异过大(即预测误差过大)，则认为存在异常.长短时记忆(Long-Short Term Memory, LSTM)网络[9-10]是此类方法的代表，该网络相比于传统的神经网络，可以对序列数据之间的时间关联性进行记忆，在时间序列预测问题中应用广泛.

本文以智能汽车为研究对象，重点研究了传感器数据异常检测和车辆运动异常检测.具体而言，根据不同传感器数据的特点(是否为时序数据)，使用基于超限学习框架的自动编码器检测瞬态异常，使用多层LSTM检测过渡异常，并提出了一种自适应确定重构误差或者预测误差阈值的方法.基于车辆自行车运动学模型，利用Kalman滤波，通过对预测值和量测值残差的正态性进行检验来检测车辆运动是否异常.实际场地测试验证了本文所提出的方法可以有效检测非时序和时序传感器数据异常，并对车辆运动是否异常进行检测.

2 传感器数据异常检测

记从某传感器获得的数据为

V={V1,V2,…,Vi,…}

(1)

其中，下标表示在第1, 2, …,i, …个时间步获得的传感器数据.对某一具体的时间步i，其获得的传感器数据通常可以表示为一个向量，如下式.

Vi=(Vi1,Vi2,…,Vij,…)

(2)

这里，Vij表示在时间步i某个分量j的值.

Sharma等人总结了4类典型的传感器故障[11-12]，包括：(1) 短时强干扰(Short)：两个连续传感器数据帧之间有较为剧烈的变化；(2) 偏离(Bias)：与实际值之间存在固定偏差；(3) 阻塞(Jam)：传感器输出为一常值；(4) 数据帧丢失(Miss)：一段时间内缺少可用的传感器数据.

Bahavan等根据检测异常值方式的不同将异常分成了两类[13]：(1) 瞬态异常：数据之间不存在时序关联性，某个采样点数据值本身即可反应研究对象是否异常；(2) 过渡异常：数据之间存在时序关联性，某个采样点数据值本身无法反应异常与否，但是连续数据帧之间的变化则可以反应研究对象是否异常.则短时强干扰和数据帧丢失可以视为瞬态异常，偏离及阻塞可以视为过渡异常.

本节介绍针对这两种不同类型异常的检测方法.采用超限学习框架下的自动编码器(Extreme Learning Machine based Autoencoder, ELM-AE)对传感器数据中的瞬态异常进行检测；采用长短时记忆 LSTM网络学习时序数据之间的时序关联性对过渡异常进行检测.

2.1 基于ELM-AE的瞬态异常检测

自动编码器(Autoencoder, AE)是一种基于数据重构进行异常检测的方法，这类方法的基本假设是[7]：正常数据可以被很好地重构，异常数据则不能.如果重构的数据与数据本身差异过大(即重构误差过大)，则认为可能存在异常.

自动编码器是一个带有一层或多层隐藏层的前馈神经网络，但是其输入和目标输出完全一致.针对异常检测任务，要求训练数据中正常样本数量远远大于异常样本数量.图1示意了一个单隐层自动编码器，其编码和解码操作分别由式(3)和式(4)描述[14].

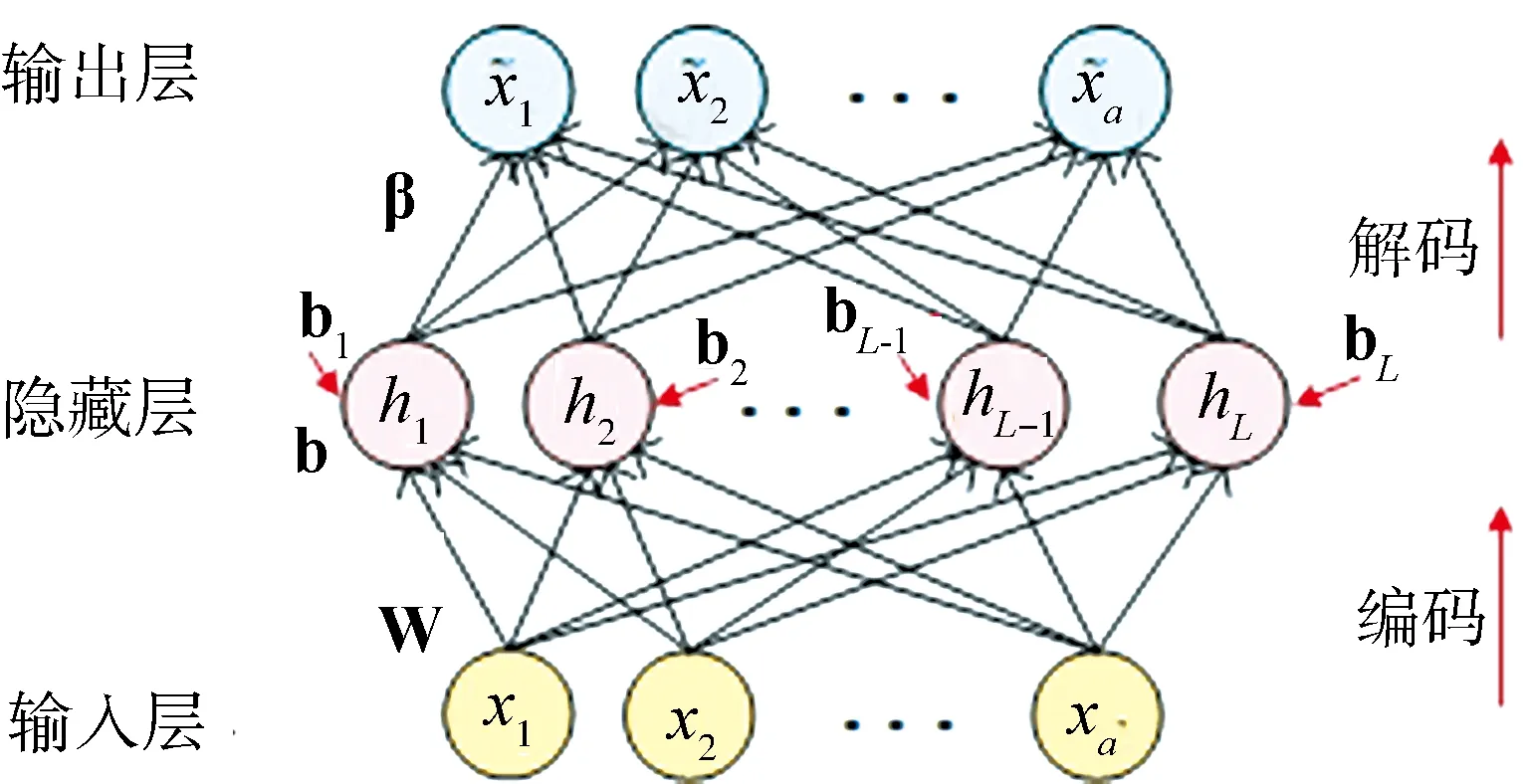
图1 自动编码器示意图Fig.1 Schematic of the autoencoder

(3)

(4)

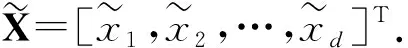
传统的自动编码器一般利用反向传播算法，通过最小化式(5)所定义的重构误差.

(5)

对权重矩阵w，β及偏置向量b进行优化.这里，‖•‖代表某种范数，本文中所有参与范数计算的向量都会被线性映射到[-1, 1]区间后再进行范数计算，下同.训练过程往往需要大量数据才能收敛.本文则采用超限学习框架构建自动编码器，该框架下，隐层参数是基于最小二乘方法直接计算得到[14]，即，通过最小化式(5)定义的重构误差，计算最优的输出层权重矩阵β*[15],如下式.

β*=H†X

(6)

其中，H=[hT(x1),…,hT(xd)]T，H†=(HTH)-1HT是矩阵H的Moore-Penrose广义逆.为了获得更好的泛化能力，可以加入正则化项来计算β*[15],如下式.

(7)

其中，I是单位矩阵；C是一个可调的参数，用于对模型的精度和泛化能力进行权衡.解算出输出权重矩阵β后，模型的输出就可以表示为

(8)

对于待检测的样本点Xnew，决策其是否为异常点的决策变量可以形式化为

D0=sign(δ-‖Y-Xnew‖)

(9)

式(9)中，δ为重构误差的阈值；sign表示符号函数；D0为决策变量，D0如果为-1则认为该样本点为异常点.阈值δ由式(10)、式(11)自适应地决定，这里，ϒ是一个随着误差‖Y-Xnew‖动态变化的系数，max(err)指训练数据再次输入训练好的模型，经过前向传播计算出的最大重构误差.

δ=γ·max(err)

(10)

(11)

分析式(10)和式(11)可得，max(err)实际上是阈值δ的下限，因为训练数据均为正常数据点，故而阈值应该大于max(err).系数ϒ可以看做是对异常数据灵敏度的一种度量，其值越小，则阈值δ也越小，对异常点的检测越灵敏.可以看到，ϒ随着误差‖Y-Xnew‖增加单调递减，正常点误差较小，则对应的阈值δ较大，说明该方法确定的阈值对正常点不敏感；异常点误差较大，其对应的阈值δ就偏小，说明该方法所确定的阈值对异常点较为敏感.

2.2 基于LSTM 的时序数据异常检测

针对时序数据的异常检测任务，根据数据之间的时间关联性，利用历史数据对当前时刻的数据进行预测.如果预测值和传感器量测值之间差异过大(即预测误差过大)，则认为可能存在异常.

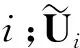
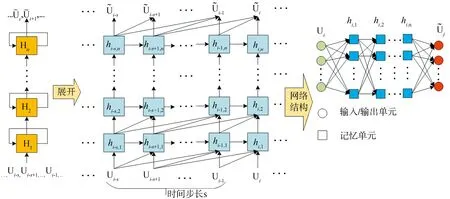
图2 多层LSTM网络结构示意图Fig.2 Schematic of multi-layer LSTM

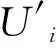
(12)

为训练目标，利用后向传播算法(Back Propagation, BP)进行训练.测试时，对于待检测的样本点Unew，判断其是否为异常点的决策变量D1与(9)式类似，形式化为

(13)

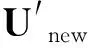
(14)

(15)

3 车辆运动异常检测

车辆的运动遵循一定的运动学及动力学规律，利用这些规律可以对车辆的运动进行建模，利用模型对当下的车辆状态进行预测.在传感器数据没有异常的情况下，如果模型预测值与实际量测值之间有着较大差距，则认为车辆运动可能存在异常.本文采用车辆自行车模型[17]对车辆进行运动学建模，设计Kalman滤波器对车辆当前状态进行预测，从瞬时和长期两个方面对车辆运动是否存在异常进行检测.

3.1 车辆自行车运动学模型

车辆自行车模型[17]是一种有效简化车辆运动的模型，其示意图如图3所示.

图3 车辆自行车运动学模型示意图Fig.3 Schematic of the vehicle bicycle kinematic model

图3的模型中的系统状态可以表示为Ω(k) = [x,y,φ]T，这里，k代表时刻；x,y表示车辆中心坐标；φ代表车辆当前偏航角.车辆当前状态与上一时刻状态的关系式可以表示为

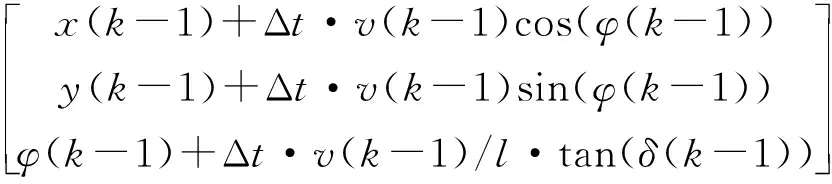
(16)

这里，Δt表示传感器数据采样周期；δ表示前轮转角；v代表车辆当前的纵向速度；l代表前后车轮的半轴长.为了进一步简化模型，本文只对x,y两个坐标值进行预测用于运动异常的检测，则(16)式可以简化为(17)式表示的线性模型.

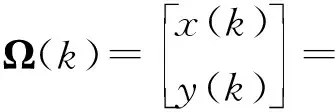
(17)

这里，

3.2 卡尔曼滤波器设计

卡尔曼滤波器是一种广泛运用的线性状态估计器，只需要前一时刻的状态估计和当前时刻的量测值，利用已知的线性状态转移模型(如式(17)所示)，就可以得到当前状态的预测值.卡尔曼滤波的过程大致可以分为两个阶段[18]，即预测和状态更新.在预测阶段，有

Ω(k|k-1)=FΩ(k-1|k-1)+BU(k)

(18)

P(k|k-1)=FP(k-1|k-1)FT+Q

(19)

这里，Ω(k|k-1)是利用上一时刻状态对当下时刻的先验状态估计，Ω(k-1|k-1)是k-1时刻系统的状态;U(k)=[a(k),δ(k)]T为控制输入，本文中的控制输入为车辆的纵向加速度a(k)和前轮转角δ(k);B是控制输入的参数矩阵;P(k|k-1)和P(k-1|k-1)分别是Ω(k|k-1)和Ω(k-1|k-1)对应的协方差矩阵;Q是过程噪声矩阵;F为一步状态转移矩阵，即(17)式中的系数矩阵.在状态更新阶段，有

Kg(k)=P(k|k-1)HT/

(HP(k|k-1)HT+R)

(20)

Ω(k|k)=Ω(k|k-1)+Kg(k)(Z(k)-

HΩ(k|k-1))

(21)

P(k|k)=(I-Kg(k)H)P(k|k-1)

(22)

其中，Kg(k)为k时刻的卡尔曼增益;H为测量矩阵;R为观测噪声矩阵;Z(k)为k时刻传感器量测值;I为适阶单位矩阵.

3.3 运动异常检测

对于车辆的运动异常检测，本文从瞬时和长期两个角度进行考虑.从瞬时角度看，当下时刻的预测值Ω(k|k)如果和量测值Z(k)差异过大，则认为车辆的运动或存在异常，即决策变量D2形式化为

D2=sign(σ-‖Ω(k|k)-Z(k)‖)

(23)

其中,σ为一阈值;‖•‖代表某种范数.如果决策变量值为-1，则认为该时刻车辆运动状态可能存在异常.

根据中心极限定理，随机误差应服从正态分布，则从长期角度，可以通过检验一段时间内卡尔曼滤波的预测值和传感器实际量测值之间残差的正态性来检测车辆的运动状态是否异常.本文选用Jarque-Bera测试[19]进行残差的正态性检验，该方法假定如果一个样本来自于服从正态分布的数据，那么其期望的偏度(skewness)是0而峰度(kurtosis)是3，通过测试样本偏度和峰度与正态分布的匹配性来对样本的正态性进行检验.记测试统计量为JB，定义为

(24)

式(24)中，n是自由度，如果假设每个样本都是独立的，那么n就等于样本数；S代表偏度;K代表峰度，计算式为

(25)

(26)

4 试验结果与分析

本节介绍文中有关算法的试验验证.首先对采集的数据进行说明，接着分别展示文中所提算法对瞬态传感器数据异常、时序数据异常以及车辆运动异常的检测效果.

4.1 训练数据采集

本次实验采集的数据为GNSS数据和惯导数据，式(2)具体化为

Vi=(lati,loni,ωxi,ωyi,ωzi,axi,ayi,azi)

(27)

式(27)中，下标i表示在某个具体时间步i.lat,lon表示由GNSS传感器获得的纬度和经度(单位：°)数据，ωx,ωy,ωz分别表示x轴、y轴、z轴方向的角速度(单位：(°)/s，ax,ay,az分别表示x轴、y轴、z轴方向的加速度(单位：g).

实验中将采集数据的组合导航设备固定于智能汽车平台(图4(a))内部，在长安大学车联网与智能汽车测试基地(图4(b))采集了部分场景的GNSS数据及惯导数据，采样频率50 Hz.针对采集数据不同步的问题，采用线性插值的软同步方法实现不同频率传感器时间同步[20].

(a) 智能汽车平台 (a) Intelligent vehicle platform

4.2 ELM-AE瞬态异常检测性能验证

在式(27)定义的8个分量中，ωx,ωy,ωz,ax,ay,az连续数据帧之间的时间关联性较弱，若存在异常可视为瞬态异常.本小节以这6个分量为训练数据，从训练时收敛速度和故障检测性能两个方面，对比了ELM_AE和传统BP网络框架下的自动编码器.二者的网络结构均设计为三层的前馈网络，隐藏层32个神经元.训练阶段，基于相同的平台(Intel Core i7-8550 CPU，27 515个训练样本)，ELM_AE的收敛速度是平均0.05 s，传统BP网络框架下的自动编码器收敛速度为平均3.54 s.

测试阶段，由于采集的数据均为正常数据，为了验证ELM-AE的检测性能，实验数据中注入了一些人工标注好的短时强干扰数据.实验采用受试者操作特征曲线(Receiver Operating Characteristic curve, ROC curve)及其曲线下面积(Area Under Curve, AUC，越接近1表征性能越好)作为度量指标，ELM_AE和传统BP网络框架下的自动编码器的ROC曲线如图5所示，其曲线下面积分别为0.761 3和0.743 4.可以看到，相比于传统BP网络框架下的自动编码器，ELM_AE的性能也有一定提升.

图5 传统自动编码器和ELM-AE的ROC曲线Fig.5 ROC curves of traditional autoencoder and ELM-AE

4.3 LSTM时序数据异常检测

本文采用多层LSTM对时序数据异常进行检测，在式(27)中，lat,lon分量连续数据帧之间有着较强的相关性，模型将以式(27)中的8个分量作为输入，对lat,lon分量进行预测.

LSTM网络结构为：输入层有8个神经元对应式(27)的8个输入，输出层有两个神经元对应预测的lat,lon分量，中间构建了2层LSTM层，每层均有16个LSTM记忆单元.输入的时间步长s被设置为30.

训练阶段，以lat,lon分量预测值和lat,lon实际量测值的均方误差(Mean Squared Error, MSE)最小化为训练目标对模型进行训练.测试阶段，由于采集的数据均为正常数据，为了验证模型的检测性能，实验数据中注入了一些人工标注好的“阻塞”数据.表1展示了多层LSTM，多层感知机(网络结构与多层LSTM类似，只是用全连接层代替了LSTM层)，以及自回归模型[21]的预测结果.

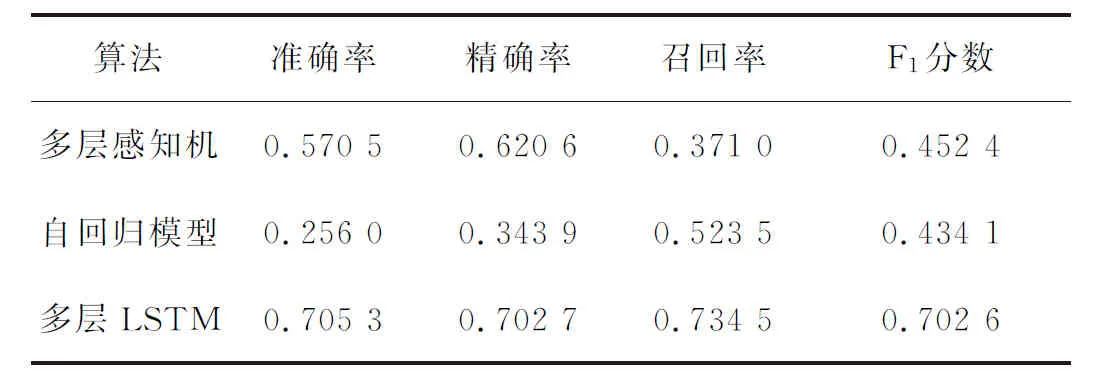
表1 几种算法时序数据异常检测性能对比Tab.1 Comparison of anomaly detection performance for several algorithms

可以看到，多层LSTM在准确率、精确率、召回率和F1分数上均获得了最好的性能，原因在于：多层感知机可以学习到输入变量之间的关系，但是该网络不具有时间记忆性，无法学习数据之间的时序关联；自回归模型则仅仅利用历史信息来进行预测，却无法学习到各输入变量之间的关联性；多层LSTM由于用记忆单元代替普通神经网络中的神经元，既可以学习到输入变量之间的关系，同时也可以学到时序数据的时间关联性，因而在处理多变量时序数据预测问题中获得了更好的性能.

4.4 残差正态性检验

本实验中采用了卡尔曼滤波观测器预测自动驾驶汽车当前的位置(即式(17)中的x,y).从长期角度看，预测值与实测值之间的残差理论上应服从正态分布.由于采集的数据都是正常数据，实验时以10 s为周期(约500个数据点)，对该周期内Kalman滤波的估计值和量测值之间的残差，用式(24)中的统计量JB进行检验.实验中JB的最大值为0.34，与0值偏差不大，可以认为对于正常数据而言，Kalman滤波估计值与量测值之间的残差是服从正态分布的.图6展示了部分周期内残差分布拟合的结果，可以直观看出其分布接近正态分布.

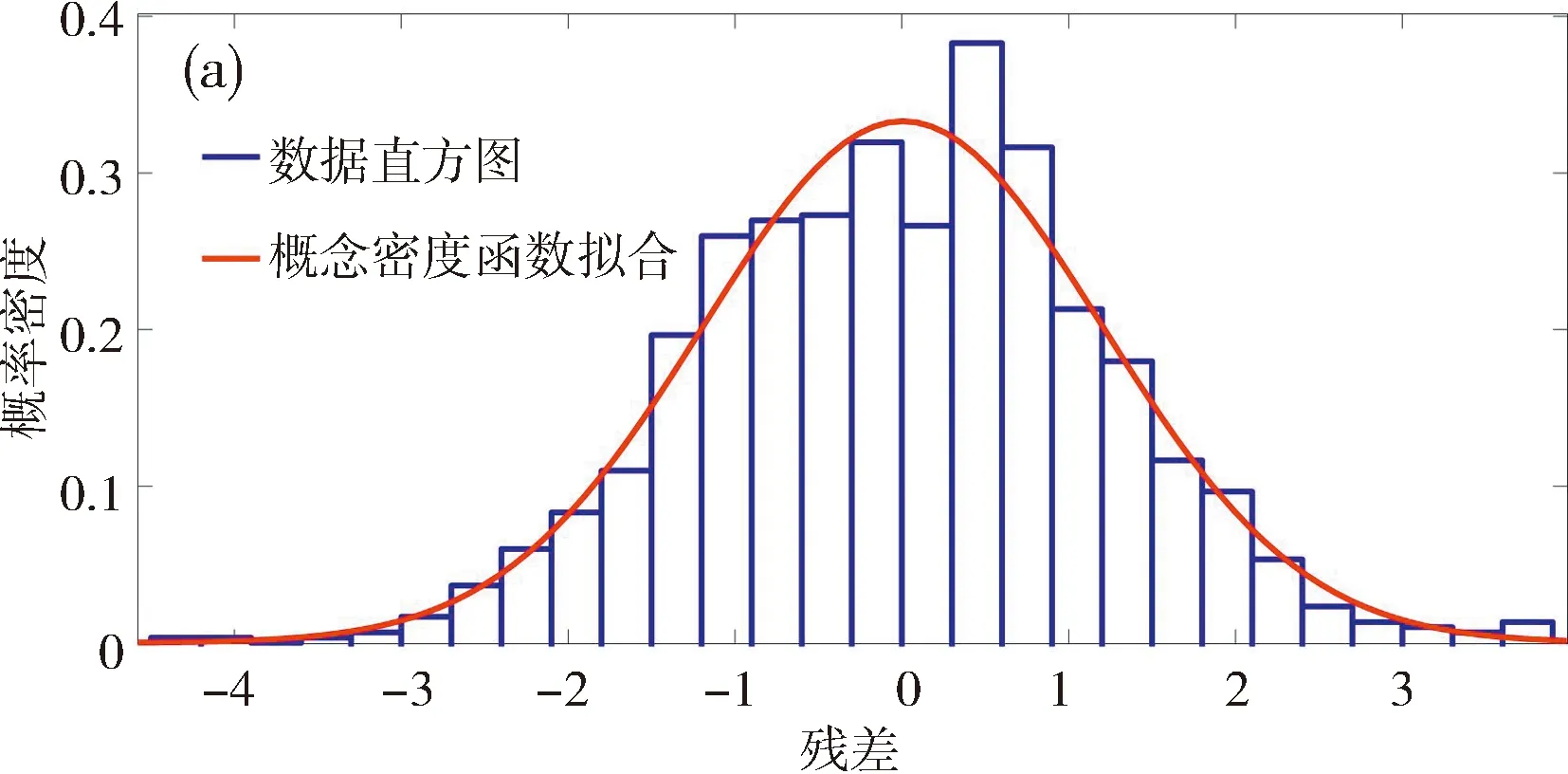
图6 残差分布拟合

5 结 论

本文基于自动编码器和长短时记忆网络，对智能汽车故障诊断的部分方法进行了研究.针对非时序传感器数据，采用超限学习框架的自动编码器重构待检测数据来检测瞬态异常；针对时序传感器数据，采用多层长短时记忆网络学习时序数据之间的关联关系预测当下时刻的数据值来检测过渡异常.与此同时，提出一种阈值随着误差大小动态变化的自适应阈值确定方法，使得决策变量对于异常值相对敏感.进一步地，采用车辆自行车运动学模型和卡尔曼滤波，利用Jarque-Bera测试对模型估计值和实际量测值之间的残差进行正态性检验以检测车辆运动是否存在异常.实验验证了本文所提出的方法可以有效检测非时序或时序异常传感器数据，并对车辆运动是否异常进行检测.