导流罩水动力特性及其对海流能机组的作用
2021-10-18高艳婧顾亚京林勇刚刘宏伟王思敏
高艳婧,顾亚京,林勇刚,刘宏伟,王思敏
(浙江大学流体动力与机电系统国家重点实验室,浙江杭州,310027)
海流能具有能量密度大、储量丰富、可预测性强的天然优势[1]。我国的海流能资源丰富,达14 000 MW,然而,大部分流域都处在低流速区,而且潮流周期的变化使流速在很长的一段时间都处于较低水平,使海流能发电机组的发电功率较小,有效的发电时间有限,因此,研究如何在低流速条件下提高海流能机组的捕获功率具有重大意义[2−3]。在低流速下提高海流能机组功率最常用的方法就是在叶轮外部加导流罩。
目前,对于海流能发电机组导流罩的研究多数采用数值仿真的方法,王树杰等[4]对4 种不同母线线型的导流罩进行了数值模拟,并初步分析了开口张角对圆型导流罩水动力学性能的影响;邓智雯等[5]利用正交表对不同结构参数下的直线型导流罩进行了数值模拟,并通过极差分析法得出了影响加速性能的结构参数的主次顺序;胡海鹏等[6]对卧式水轮机导流罩的长度以及开口张角进行了CFD仿真分析,并进行了水槽实验;陈正寿等[7]分别计算了拟定的不同形状的10 种导流罩模型结构的水动力性能,结果表明收缩段和扩张段均为双三次曲线的对称线型导流罩具有最优的水动力性能。他们的研究都是基于三段式导流罩,对于收缩段和扩张段的曲线以及结构参数进行仿真研究,得出水动力性能较好的曲线以及不同结构参数对于水动力性能的影响,但对具体增速的原理研究以及其他结构形式的导流罩[8−10]对比研究比较少,缺乏对不同导流结构水动力特性的总体分析和评价,并且大部分研究是基于二维的,COIRO 等的研究[11]显示二维仿真与三维仿真的研究结果差别较大。
本文作者基于CFD 方法,首先对9 种不同结构型式的导流罩三维仿真分析对比,得出翼型导流罩具有最佳的水动性能,接着对翼型导流罩在不同结构参数进行仿真研究,得出不同参数对其水动性能的影响,并且与二维翼型建立关系,提出翼型导流罩的设计方法,最后依据该方法设计500 W海流能机组的导流罩。
1 计算模型
1.1 导流罩的模型
选取9种导流罩型式,如图1所示。
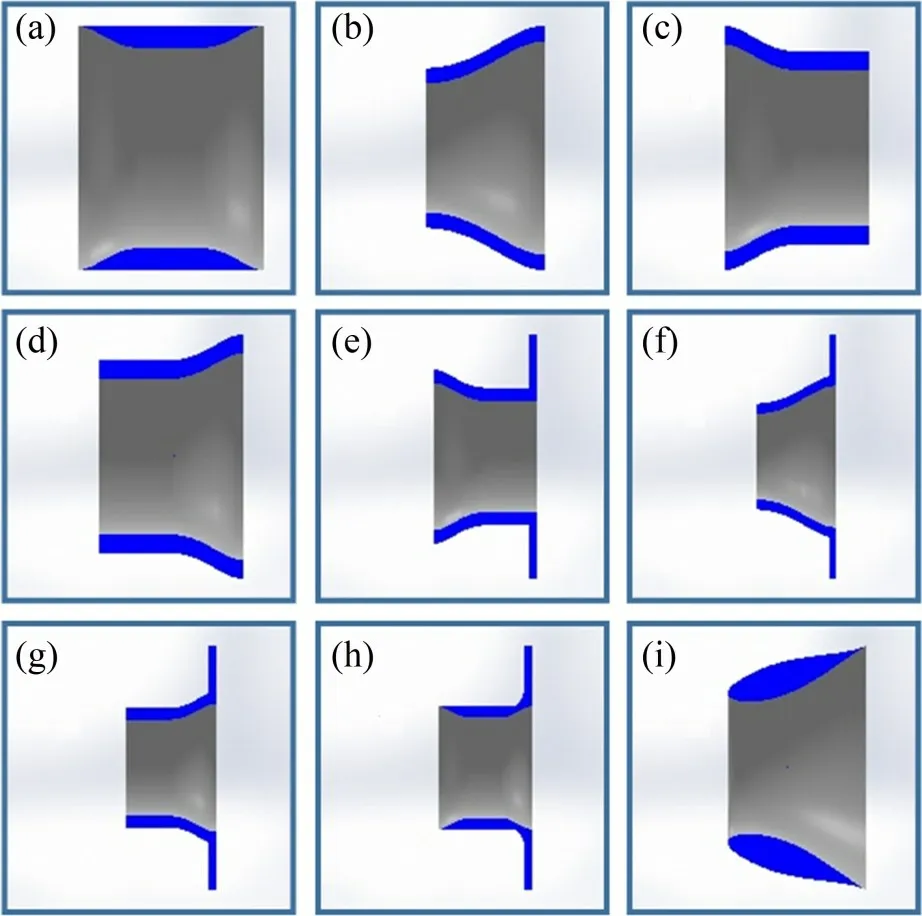
图1 不同型式的导流罩示意图Fig.1 Schematic diagrams of different types of diffuser
导流罩1是典型的三段式,包含收缩段、直线段和扩张段,收缩段和扩张段线型采用水动力性能好的维氏曲线[12];导流罩2,3和4是三段式中的部分,采用仿真方法分析扩张段、直线段和收缩段各部分的增速原理(导流罩3和4对称,尺寸完全相同);导流罩5在导流罩3的基础上增加了凸缘结构;导流罩6在导流罩2的基础上增加了凸缘结构;导流罩7是在导流罩6的基础上增加了直线段;导流罩8在三段式的基础上增加了凸缘结构;导流罩9采用翼型结构,为了进一步定量分析,将导流罩8作为对照组,控制导流罩8和导流罩9的最小直径d、最大直径D以及长度L相等,分别为50,86和60 cm。
1.2 网格划分和边界条件
在ICEM 中完成部分建模、网格划分,如图2所示,计算流域直径取导流罩最大直径的4倍,上游、下游流域直径分别为导流罩最大直径的5倍和6 倍[13],前8 种类型导流罩采用结构化网格,翼型导流罩9 采用非结构化网格,近壁都要加密处理,控制量纲为一的壁面距离y+约等于1。

图2 导流罩的计算网格Fig.2 Computational grids of diffuser
为了保证求解的准确性,首先需要验证网格的无关性,利用导流罩9颈处截面中3个点的速度(见图3,其中,点1坐标为(0.28,0,0),点2坐标为(0.28,0,0.08),点3 坐标为(0.28,0,0.16),单位为m)作为评判标准,如图4所示。由图3可知:当网格数量达到76万个时,导流罩颈处截面中3个点的速度基本不变,确定导流罩9网格的数量为764 958个,外流域网格直径为0.15 m,翼型导流罩的网格直径为0.015 m。
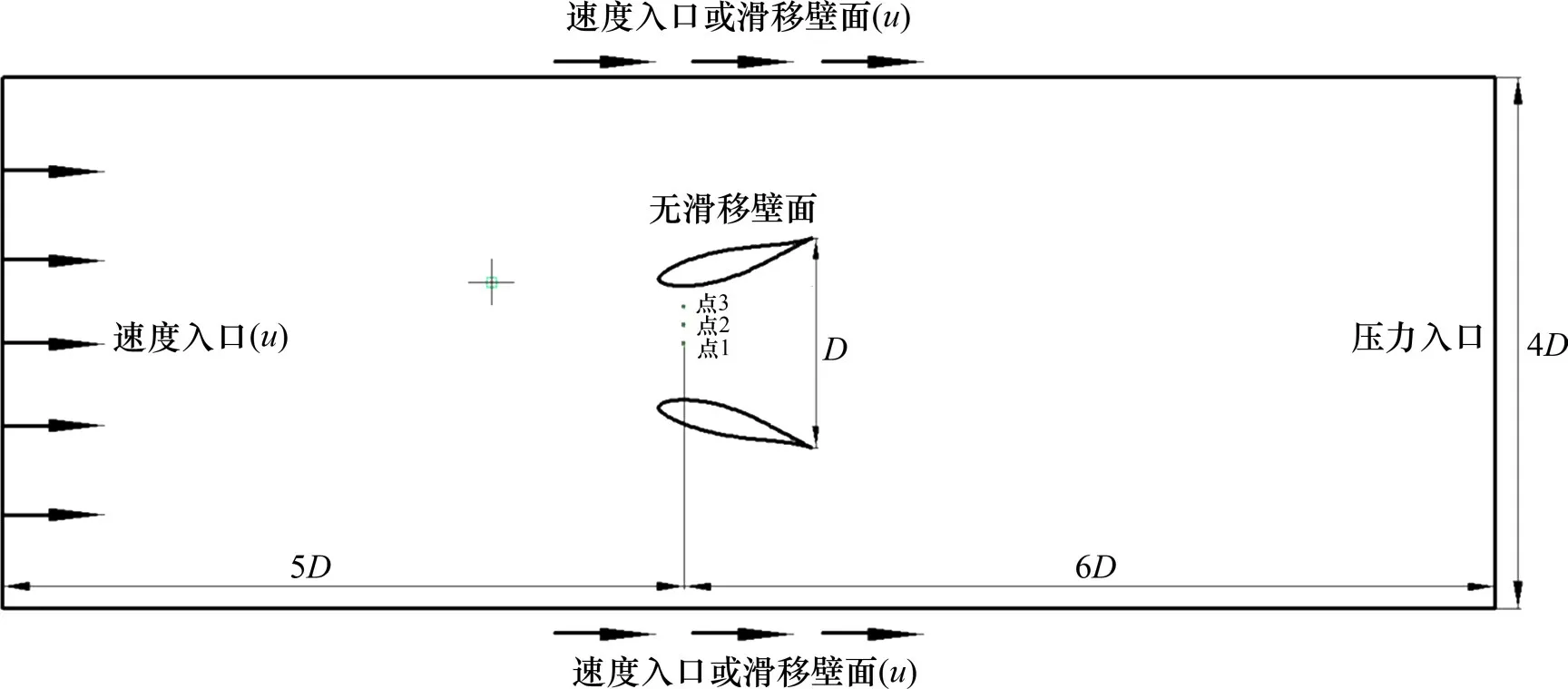
图3 计算域和边界条件Fig.3 Calculation domain and boundary conditions
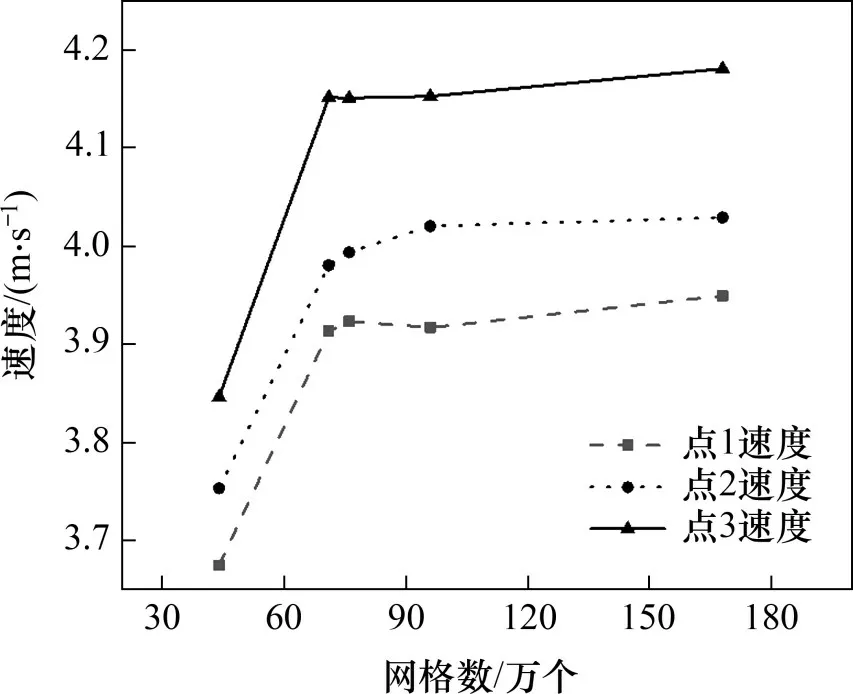
图4 网格无关性验证Fig.4 Independence verification of grid
计算域入口采用速度入口(u=2 m/s),出口为压力出口,流域壁面设为速度入口或滑移壁面(u=2 m/s),导流罩壁面设为无滑移壁面[14],如图3所示。
研究选择SSTk−w湍流模型[15−16],运用Segregated隐式求解器,压力速度耦合采用SIMPLE算法确定,梯度采用格林−高斯节点法(Green-Gause node-based method)确定,压力、动量、湍流动能和比耗散速率采用二阶离散化方法[16]确定。
2 不同结构导流罩仿真结果分析
不同导流罩速度矢量图和水流流速分别如图5和图6所示,其速度是在速度稳定段建立线监测,得出的沿导流罩径向的速度。
从图5可以看出:扩张段降低压力,形成涡旋产生负压,吸收更多的流体,从而提高流速,但仅依靠负压增速并不会产生一个稳速段(导流罩6类似),需加入直线段,结合图6分析导流罩4在靠近导流罩边缘处速度会迅速降低(与导流罩7 类似),这表明收缩段是必要的,便于流体流入,起到过渡作用;在进入导流罩3之前,水流速度比无限远处的速度略微降低,直线段与收缩段相比面积减小,基于流体连续性方程,由于直线段与收缩段相比面积减少,所以,直线段速度增大,但分析图6曲线中导流罩3 和导流罩4 的增速效果可知,利用负压增速的效果比聚流增速的效果好,这表明高性能的导流罩需加入扩张段。导流罩5在导流罩3 的基础上增加凸缘结构,由速度矢量图5(e)可以看出在凸缘后部形成涡产生负压,吸引更多流体,从而使流体流速增大,与导流罩2增速的原理一样。将导流罩2和导流罩5叠加,设计了导流罩8,从图6可看出导流罩8 的增速效果最好。由此可以得出高性能的导流罩包含流入段、稳速段和负压段这3个阶段。其中,流入段引导更多的流体进入导流罩,稳速段在导流罩内形成稳定的速度区间,负压段产生负压,吸收更多流体进一步增大导流罩内流体速度。另外,从流动本质上结合导流罩1 的速度矢量(图5(a))分析,流入段和稳速段为顺压梯度区(沿流动方向,流速递增,压强递减),稳速段和负压段为逆压梯度区(沿扩张方向,流速减小,压力逐渐升高),这说明高性能的导流罩应包含顺压梯度区和逆压梯度区。

图5 不同导流罩速度矢量图Fig.5 Velocity vector diagrams of different types of diffuser
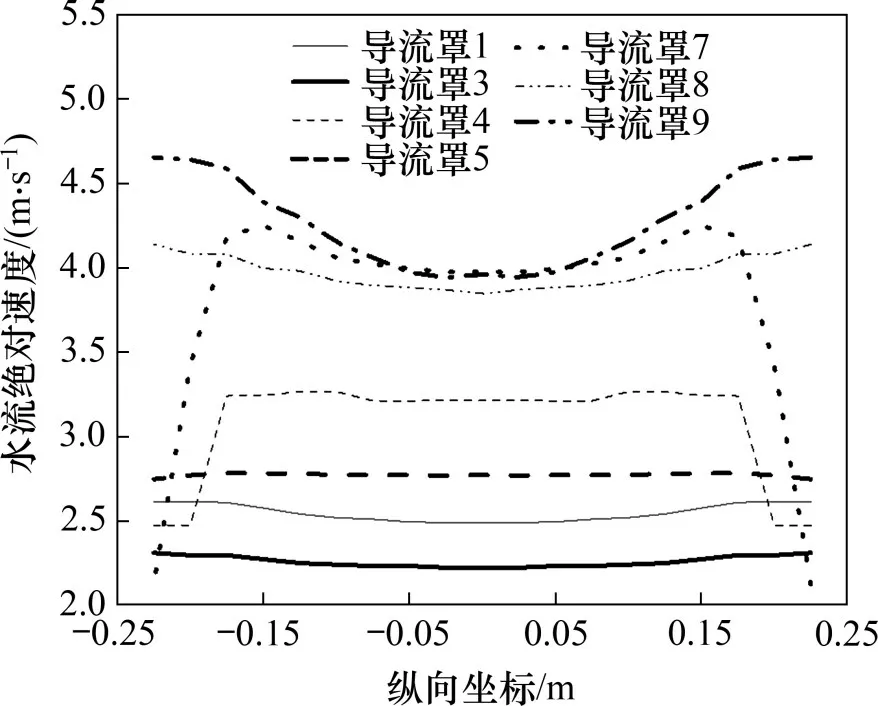
图6 不同导流罩内水流速度对比Fig.6 Comparisons of different types of diffuser'water flow velocity
二维翼型吸力面的边界层的流动示意图如图7所示。图7中,1~3 区为顺压梯度区,3~5 区为逆压梯度区,S为流动分离点(在S点流动从壁面分离,该点壁面剪应力为0),这样的流动特性决定了可以利用翼形的吸力面满足高性能导流罩的结构要求。由图5(f)和图6可以看出:翼型导流罩9形成的流速稳定区域虽然比导流罩8的小,但在稳定区,导流罩9 的增速效果比导流罩8 的效果好,并且随纵向坐标的增大,水流的增速更大,再加上导流罩8 的凸缘结构的存在使轴向力更大(尤其是在复杂的海域条件下)。总体来看,翼型导流罩的水动能性能更好。

图7 二维翼型边界层流动示意图Fig.7 Schematic diagram of 2D airfoil boundary layer flow
3 翼型导流罩的设计分析
FRANKOVIĆ 等[17−18]发现翼型作为导流罩通过提供升力产生的上下压差可以增加叶轮输出功率,增速性能好的导流罩要求翼型具有高升阻比,经CFD仿真发现,相对弯度为4%且厚度较小的翼型具有较好的升阻比特性[19]。下面以相对弯度为4%的NACA-63418翼型为研究对象,研究翼型导流罩的性能。
3.1 翼型导流增速与攻角、弦长、内径的关系
控制翼型导流罩的最小直径(颈处直径)为20 cm,弦长为20 cm,改变攻角为8°,10°,13°,14°,15°,16°和20°,仿真研究增速性能以及分离点位置与攻角的关系,结果如表1所示。控制翼型导流罩最小直径(颈处直径)为20 cm,攻角为15°,改变弦长为20,40,60和80 cm,仿真研究增速性能以及分离点位置与弦长的关系,结果如表2所示。控制翼型导流罩的弦长为20 cm,攻角为15°,改变内径为5,10,20,80和100 cm,仿真研究增速性能以及分离点位置与内径的关系,结果如表3所示。在颈处位置建立线监测得到速度取值范围,依据导流罩表面的压力曲线得出分离点位置(分离区内的压力近似等于分离点处的压力),即分离点S的x坐标翼型前缘被定义为原点,从翼型前缘到后缘沿弦长方向被定义为x轴的正向。
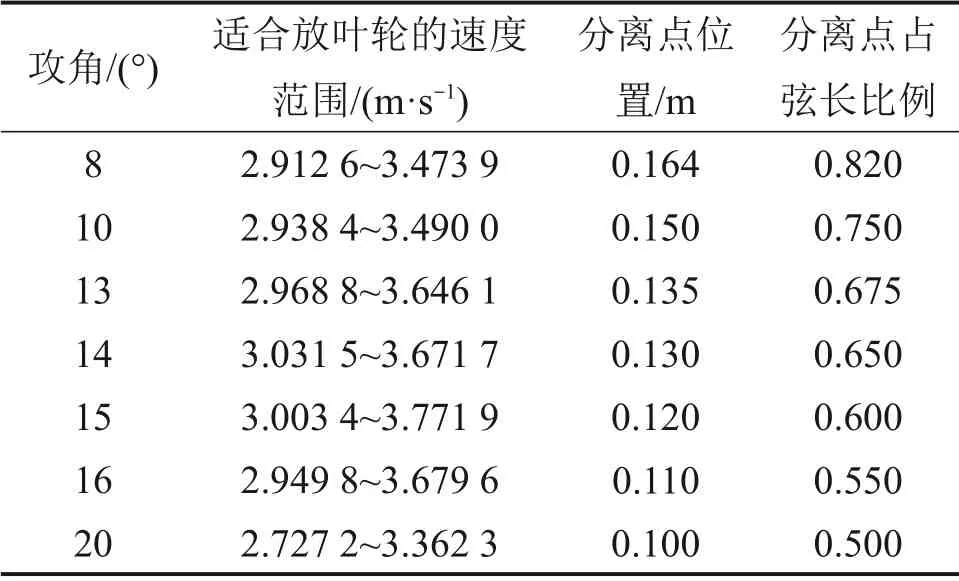
表1 不同攻角下翼型导流罩的增速与分离点对比Table 1 Comparisons of velocity and separation point of airfoil diffuser at different angles of attack
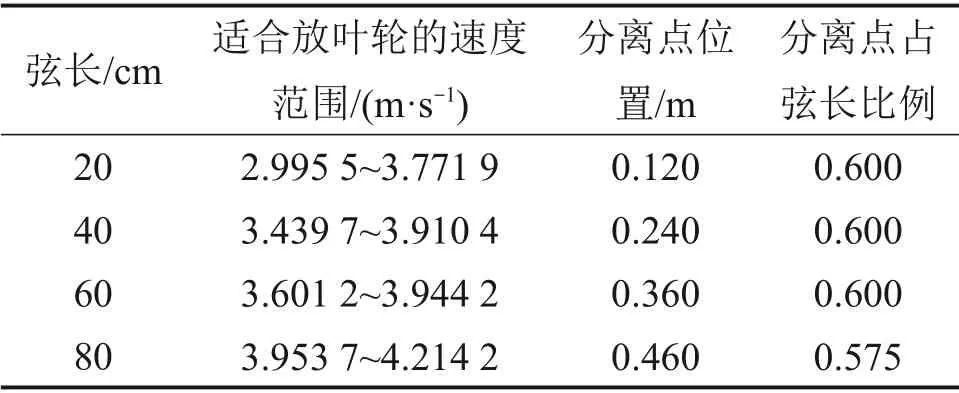
表2 不同弦长下翼型导流罩增速与分离点对比Table 2 Comparisons of velocity and separation point of airfoil diffuser at different chord lengths

表3 不同内径下翼型导流罩增速与分离点对比Table 3 Comparisons of velocity and separation point of airfoil diffuser at different inner diameters
从表1可以看出:选取的适合叶轮放置的稳速段速度随翼型导流罩攻角增大,呈先增大后减小的趋势,在攻角为15°时取得速度的最大值,这与二维翼形升力系数随攻角的变化趋势一致[20]。结合图8的速度矢量图分析,分离点随翼型导流罩攻角的增大前移,分离程度越来越大。
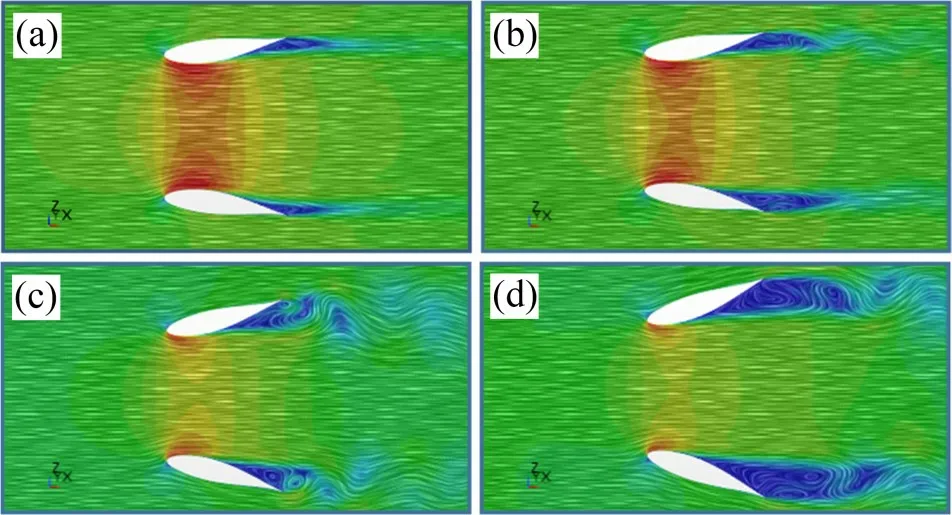
图8 不同攻角下翼型导流罩的速度矢量图Fig.8 Velocity vector diagrams of airfoil diffuser at different angles of attack
从表2可以看出:选取的适合叶轮放置的稳速段速度随导流罩弦长的增加呈现增大的趋势,导流罩内的负压区域也更大,这与二维翼型升力系数随弦长的变化趋势是一致的[20]。结合图9的速度矢量图分析,在内径一定的情况下,弦长增加1~2倍,分离点的位置基本不发生改变。
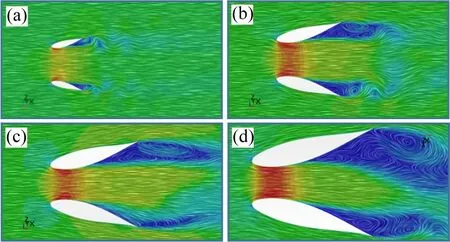
图9 不同弦长下翼型导流罩的速度矢量图Fig.9 Velocity vector diagrams of airfoil diffuser at different chord lengths
从表3可以看出:选取的适合叶轮放置的稳速段速度随导流罩内径的增大呈现减小的趋势。结合图10的速度矢量图分析,分离点随直径的增大后移,分离程度越来越小,在内径为80 cm 和100 cm时,内部不发生流动分离。
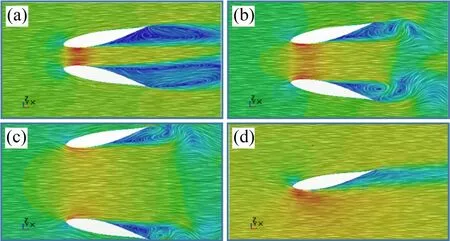
图10 不同内径下翼型导流罩的速度矢量图Fig.10 Velocity vector diagrams of airfoil diffuser at different inner diameters
3.2 翼型导流增速最优攻角与弦长、内径的关系
基于翼型导流罩分离点随弦长的变化趋势,控制翼型导流罩的最小直径为20 cm,改变弦长为20,40,60,80 和100 cm,分别在不同的攻角下模拟翼型增速最优攻角与弦长的关系,结果如表4所示。基于翼型导流罩分离点随内径的变化趋势,控制翼型导流罩的弦长为20 cm,改变内径为5,10,20,80 和100 cm,分别在不同的攻角下仿真研究翼型导流增速最优攻角与内径的关系,结果如表5所示。
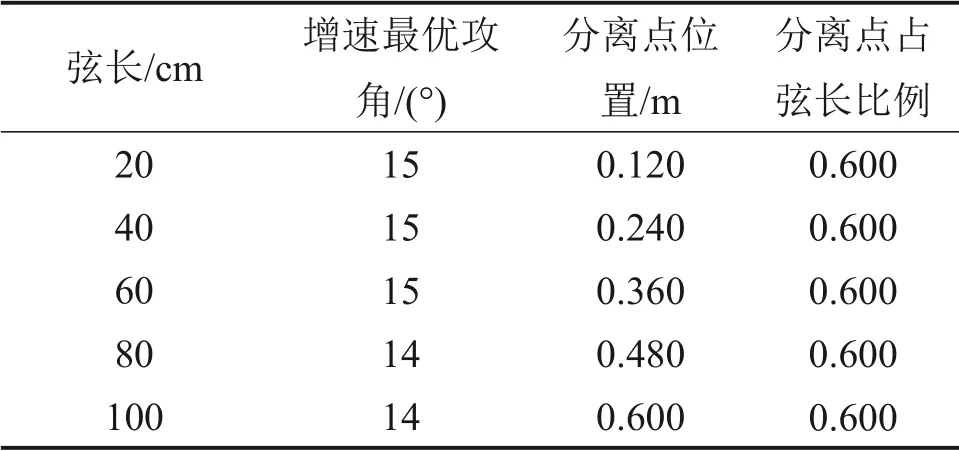
表4 不同弦长下翼型导流罩增速最优攻角对比Table 4 Comparisons of the optimal angle of attack of airfoil diffuser at different chord lengths
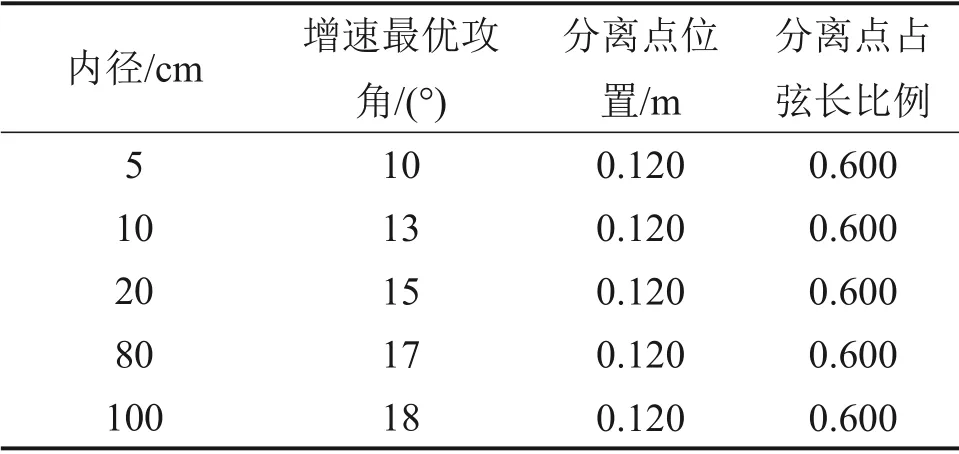
表5 不同内径下翼型导流罩增速最优攻角对比Table 5 Comparisons of the optimal angle of attack of airfoil diffuser at different inner diameters
从表4可以得到:在翼型导流罩最小直径一定时,翼型弦长增大1~2倍,增速最优攻角不变或减小1°,这与二维翼型临界攻角对于长度(雷诺数)改变不敏感相吻合[20]。
从表5可以得到:在翼型导流罩弦长一定时,导流罩增速最优攻角随着导流罩内径的增大而增大(内径增大1 倍,增速最优攻角增大2°左右,这可以作为后面增大程度预测的参考)。
3.3 增速最优攻角范围预测
基于增速最优攻角与内径、弦长的关系,弦长增大n倍,内径减小至原来的1/n,最优攻角的增大并不一致,内径减小引起的最优攻角的增大程度更大。选取L/d=1 为研究对象,改变弦长(内径)为5,10,15,20,80 和100 cm,分别在不同攻角下仿真确定增速最优攻角,并且在相同条件下对二维翼形在不同攻角下的升力系数进行仿真确定翼型临界攻角,仿真结果如表6所示。

表6 不同弦长下翼型导流罩增速最优攻角与翼型临界攻角对比Table 6 Comparisons of the optimal angle of attack of velocity and the optimal angle of attack of lift coefficient at different chord lengths
从表6可知:1) 在L/d=1 时,随弦长的增大,增速最优攻角增大,这是由于内径和弦长都增大,基于增速最优攻角与弦长、内径的关系,内径增大引起的增速最优攻角增大的程度比弦长增大引起的最优攻角减小的程度大;2)在L=d=15 cm时,增速最优攻角等于翼形临界攻角,当L>15 cm时,增速最优攻角大于翼形临界攻角。基于上述结论1)和二维翼型临界攻角对于雷诺数改变不敏感的特性,增速最优攻角比翼形临界攻角大的程度,随弦长增大而增大(长度增大6 倍,增速最优攻角比翼型临界攻角大1°左右,此结论可以作为后面增大程度预测的参考)。同理,当L<15 cm 时,增速最优攻角比翼形临界攻角小,增速最优攻角比翼形临界攻角小的程度,随弦长减小而增大。
在L=d=15 cm,u=2 m/s 时,增速最优攻角等于翼型临界攻角,改变弦长(内径)为30,45,60 cm和入口流速分别为1,0.667,0.5 m/s(雷诺数相同),在不同攻角下仿真确定增速最优攻角,仿真结果如表7所示。
从表7可知:翼形导流罩在相同雷诺数下具有相同的增速最优攻角(L=d),依据二维翼型,在相同雷诺数下,升力系数随攻角的曲线不变(在相同雷诺数下具有相同的临界攻角)。所以,在上述雷诺数下,增速最优攻角等于翼型临界攻角,定义该雷诺数为NACA-63418 翼型导流罩的临界雷诺数。

表7 相同雷诺数下翼型导流罩增速最优攻角对比Table 7 Comparisons of the optimal angle of attack of airfoil diffuser at identical Reynolds number
在不同的翼型导流罩弦长L和入口流速u下,定义NACA-63418翼型导流罩的临界弦长Lc,在该临界弦长下,NACA-63418翼型导流罩的增速最优攻角与翼型临界攻角相等:

式中:ρ为海水密度,ρ=1040 kg ⋅m3;μ为海水动力黏度,μ=0.00115kg/(m ⋅s)。
将上述L=d=15 cm 延伸至L=Lc,当L>Lc时,增速最优攻角比翼形临界攻角大,增速最优攻角比翼形临界攻角大的程度,随弦长增大而增大(长度增大6 倍,增速最优攻角比翼型临界攻角大1°,此结论可以作为后面增大程度预测的参考);当L 上述预估了L=d条件下的增速最优攻角,基于增速最优攻角与内径的关系预估任意内径弦长下的增速最优攻角(内径增大1 倍,增速最优攻角增大2°,此结论可以作为后面增大程度预测的参考)。 基于上面翼型导流罩水动力性能的仿真分析,总结翼型导流罩设计方法。 翼型导流罩的设计参数包含内径、弦长以及攻角,内径的选择取决于叶轮直径,弦长的选择基于前面的分析,弦长越大,导流增速性能越好。但受成本限制,弦长也不能太大。增速最优攻角的确定尤为重要。增速最优攻角的确定流程如图11所示。导流罩内径、弦长以及入口流速已知,确定同雷诺数下的二维翼型临界攻角α以及翼型导流罩的临界弦长Lc,依据3.3 节的结论得到导流罩内径d1等于弦长L条件下的增速最优攻角的范围,再基于增速最优攻角与内径的关系,确定在导流罩内径d和弦长L条件下的增速最优攻角的范围,通过这样的方法减小仿真计算量,最终通过少数量仿真确定增速最优攻角αopt。 图11 翼型导流罩增速最优攻角设计流程图Fig.11 Design flow chart of the optimal angle of attack of airfoil diffuser 深远海仪器的能源供给一直是难题,其流速偏低,同时海洋仪器的功率一般不大,在几十到几百瓦之间,500 W 海流能机组有广阔的应用前景。本文作者设计500 W机组导流罩。500 W海流能机组的叶轮半径为0.96 m,额定流速为1 m/s,叶轮额定转速为50 r/min,设计的最佳叶尖速比为5.03。 基于上述翼型导流罩设计方法,首先确定翼型导流罩的颈处直径为2.1 m,弦长为1.5 m,采用翼型导流罩增速最优攻角预估方法确定增速最优攻角范围大于14°(也可以基于翼形导流罩在相同雷诺数下(L=d)具有相同的增速最优攻角,依据表6确定L=d=1.5 m 的增速最优攻角为15°以及16°),通过15°以及16°攻角下的仿真最终确定增速最优攻角为15°。设计导流罩的三维模型如图12所示。在不考虑成本的情况下,要获得更好的性能,需增加弦长。基于增速最优攻角与弦长的关系,弦长增加1~2倍,增速最优攻角不变。 图12 500 W外加导流罩海流能机组模型Fig.12 500 W tidal current turbine with diffuser model 通过改变叶轮转速控制叶尖速比变化范围为3~7,分别对单独叶轮和外加导流罩的情况进行仿真。图13所示为海流能机组加装导流罩下的速度矢量图,图14所示为叶轮处水流速度对比。由图13和图14可知:与单独导流罩仿真一致,在放置叶轮的颈处水流轴向速度增加,对于单独翼型来说流体速度增大,使翼型压力面与吸力面的压差增大,所以,叶轮吸压力面压差增大。叶轮捕能功率公式为 图13 叶轮外加导流罩的速度矢量图Fig.13 Velocity vector diagram of tidal current turbine with airfoil diffuser 式中:P为叶轮捕能功率,W;D为叶轮直径,m;vz为轴向速度,m/s;∇p为叶轮吸力面与压力面压差,Pa;r为叶轮半径,m。由式(2)可得:加装导流罩后叶轮处的轴向水流速度和叶轮吸压力面压差都增大,导致叶轮捕获功率提高。 从图14还可以看出:随纵向坐标增大,流体增速程度更大。叶尖是速度增大程度最大的区域,由于叶轮在旋转时水流在叶片压力面产生正压力,在吸力面产生负压,且叶尖是压差最大的区域,叶轮的捕能主要来自叶尖,故翼型导流罩对于水流增速的速度分布更有利于叶轮捕获功率提高。 图14 叶轮处水流速度对比Fig.14 Flow velocity comparison at tidal current turbine 图15所示为在额定流速下,叶轮在有、无导流罩时的捕获功率随叶尖速比的关系曲线。由图15可知:叶轮外加导流罩可以明显地提高海流能机组叶轮的捕获功率,在入口流速为1 m/s,最佳叶尖速比下,单独叶轮的捕获功率为390.40 W,加装三段式导流罩(收缩段和扩张段采用维氏曲线)后叶轮的捕获功率为557.71 W,捕获功率提高了42.9%,而加装翼型导流罩后叶轮的捕获功率为632.96 W,捕获功率提高了62.1%。 图15 叶轮捕获功率随叶尖速比的变化曲线Fig.15 Curves of turbine power with tip speed ratio 单独叶轮的启动流速为0.55 m/s,启动力矩为10 N·m,在叶轮外加翼型导流罩,当入口流速为0.52 m/s 时可达到启动力矩;单独叶轮在入口流速为1 m/s及最佳叶尖速比下,输出力矩为74.6 N·m;在叶轮外加装翼型导流罩,当入口流速为0.86 m/s,叶轮转速为50 r/min 时,叶轮输出力矩可达74.98 N·m。综合这2 个方面,可以得到在叶轮外加翼型导流罩可以降低启动流速。 1)翼型导流罩具有更好的水动特性。 2)采用翼型导流罩设计方法可以在少量仿真情况下确定增速效果最佳导流罩的结构参数。 3)设计的500 W 海流能机组的翼型导流罩可以降低叶轮的启动速度,提高叶轮的捕获功率,在最佳叶尖速比下,叶轮捕获功率提高62.1%,比三段式导流罩叶轮的捕获功率高。3.4 翼型导流罩设计方法
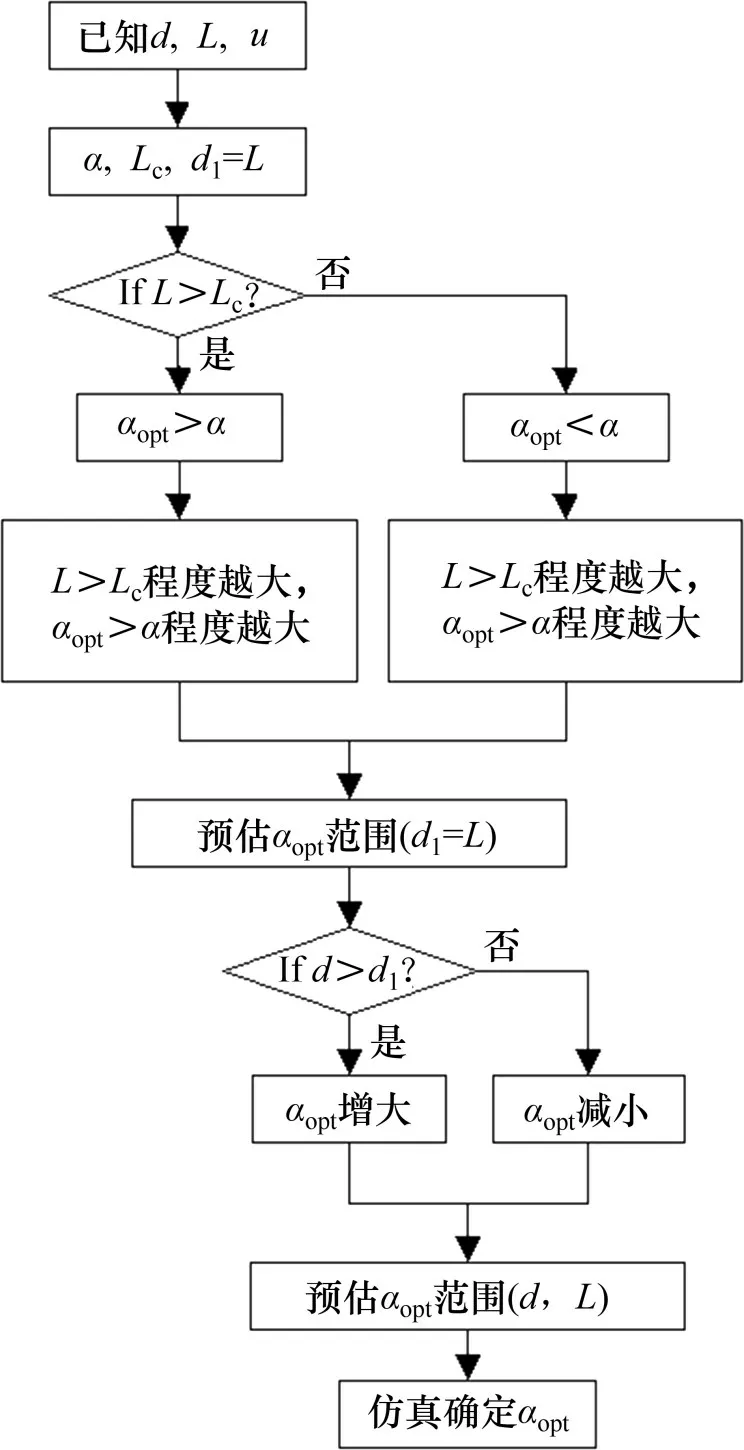
4 500 W海流能机组导流罩的设计


5 结论
