采用改进的SOR迭代法模拟一维非饱和土渗流的研究
2021-10-18罗晓辉朱帅润陈骄锐吴礼舟
罗晓辉,朱帅润,陈骄锐,吴礼舟,2
(1.成都理工大学环境与土木工程学院,地质灾害防治与地质环境保护国家重点实验室,四川成都,610059;2.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室,重庆,400074)
全球变暖增加了诸如暴雨等极端天气出现的频次,导致了众多的非饱和/饱和土浅层滑坡的地质灾害[1−4]。因此,降雨入渗的模拟对边坡稳定性分析、滑坡地质灾害等预测具有重要意义[5−10]。RICHARDS 方程[11]常被用以描述非饱和土降雨入渗问题,其中渗透系数与土−水特征曲线息息相关,获得该方程的解析解较困难[12−14],因此,地下水渗流问题常采用数值方法来近似求解[15−16]。关于降雨入渗问题的数值解或解析解[17−19]已有大量研究,例如:SRIVASTAVA等[20]使用指数函数形式表示的土−水特征曲线获得了一维均质和两层土瞬态压头分布的解析解;TRACY[21]基于线性化的RICHARDS 方程获得了RICHARDS 方程二维和三维的解析解表达式;KU等[22]使用Gardner模型线性化了RICHARDS 方程;孙长帅等[19]通过指数函数来描述土−水特征曲线、渗透系数函数,得到了关于一维非饱和土入渗过程的RICHARDS 方程的解析解。此外,用于求解可变饱和渗流问题的一些先进的数值方法在某种条件下表现出较高的数值精度、计算效率和易于实施的优点,如非正交网格的有限差分法[23]、无网格方法[24]、元胞自动机方法等[25]。例如,DOLEJŠÍ等[26]提出了自适应高阶时空不连续Galerkin方法来解决非饱和流的问题,以获得更高的效率和精度。WU 等[27]使用Chebyshev谱方法求解一维边坡的RICHARDS 方程,与有限差分法相比具有更高的精度。
虽然不同数值方法求解RICHARDS 方程具有不同的优点,但研究一种改进的迭代方法来求解由上述数值方法离散获得的线性方程组,以提高数值收敛率依然很有意义。陈曦等[18]提出了短项混合欠松弛法求解RICHARDS 方程,并对其实用性和可靠性进行了验证。此外,由于预处理可极大地加快迭代方法的收敛速度,故预处理技术也被广泛地用于各种迭代方法中[28]。LIU 等[29]提出预处理的共轭梯度法减小了病态线性系统的条件数并获得了较好的收敛效果。ZHU 等[17]提出了一种改进的双边平衡Jacobi迭代方法,可有效地求解层状非饱和土的严重病态线性方程组。WANG 等[30]提出了预处理的改进的Hermitian 和skew-Hermitian分裂迭代方法,可有效地求解分数阶非线性Schrödinger方程。
Gauss-Seidel 迭代法是求解线性方程组的一种经典并且常用的迭代方法,但是该方法的收敛速度较慢[31]。SOR 迭代法的收敛速度比Gauss-Seidel迭代法的收敛速度高,但是其松弛系数的选择是较困难的[31]。然而,根据迭代矩阵的最小谱半径可以确定最优松弛系数,结合矩阵分裂和预处理技术,SOR 迭代法的收敛率可以得到进一步提高,因此,提出了2 种改进方式的SOR 迭代,即红黑排序SOR 迭代法(RB-SOR)和采用对角尺度化预处理子的预处理SOR迭代法(P-SOR)。
本文作者首先采用GS 和SOR 及2 种改进的SOR 迭代算法求解稳态和瞬态的线性化RICHARDS 方程,讨论在不同网格长度下预处理技术对系数矩阵条件数的影响情况,进而讨论4种方法的收敛速度,以及在不同网格长度和时间步长下改进的SOR 方法相对于传统方法(GS 和SOR)的加速情况;同时,在不同网格长度和时间步长下,对采用不同迭代方法获得的数值解与解析解之间的均方根误差进行比较,以检验其数值精度和稳定性。
1 控制方程和离散化
RICHARDS 方程通常被用来描述非饱和土体中地下水渗流问题,其三维压力水头(h)形式的RICHARDS方程(RE)可以写成[11]
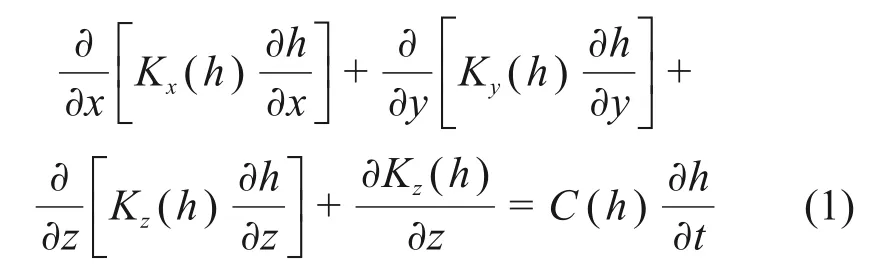
式中:Kx(h),Ky(h)和Kz(h)分别为相对于x,y和z方向的渗透系数函数;h为压力水头;C(h)为容水度。由于土水特征曲线是非线性的,容水度可以描述为

式中:θ为含水率。求解RICHARDS方程需要3个特征函数,即非饱和土渗透系数函数、土水特征曲线以及含水率函数。将式(2)代入式(1),对于一维非饱和土垂直入渗的RICHARDS方程可简化表示为
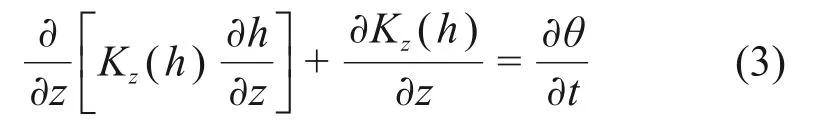
式中:z为垂直坐标。对于非饱和土体中的渗透系数和含水量函数,GARDNER提出如下指数形式[14]:
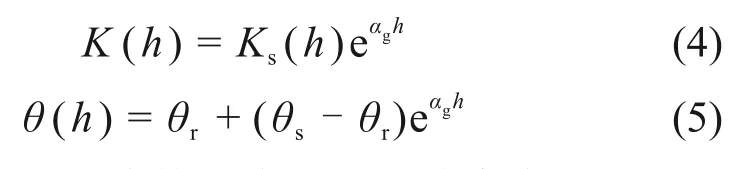
式中:θs和θr分别为饱和含水量和残余含水量;Ks为土体的饱和渗透系数;αg为土体的孔隙大小分布参数。为了线性化RICHARDS 方程,通常先将非饱和土的渗透率进行归一化,则相对渗透系数Kr可表示为
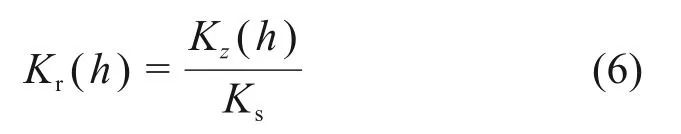
进而,引入一个新的参数h*,定义为

式中:χ为常数,χ=eαghd;hd为干燥土的压力水头。因此,对式(7)相对于z轴进行求导,可得
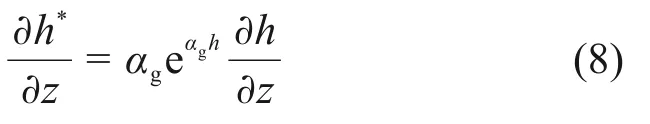
从式(7)可以看出0 ≤h*<1,因此,

进而对式(5)求导,可表达为

因此,将式(8)~(10)代入式(3),可获得线性RICHARDS方程:

式中:c=αg(θs-θr)/Ks。
采用有限差分方法(FDM)来离散式(11),获得1 个近似解。对于空间离散化,使用中心差分格式;对于时间离散,采用隐式格式。因此,1D 线性化RICHARDS方程的有限差分格式可表示为
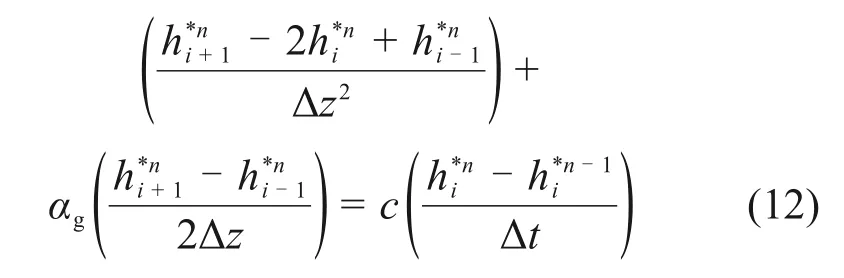
式中:i为沿z轴方向的离散节点;Δz为离散的空间步长;Δt为离散的时间步长;n为时间节点。考虑稳态情况时,其有限差分格式可简化如下:

式(12)和式(13)所构成的线性方程组可写成矩阵形式:

式中:A,h*和f分别为N×N阶方阵、N×1 列向量和N×1 列向量。式(14)可采用相关迭代法进行求解,一旦获得数值解h*,实际的压力水头可以通过如下公式换算:
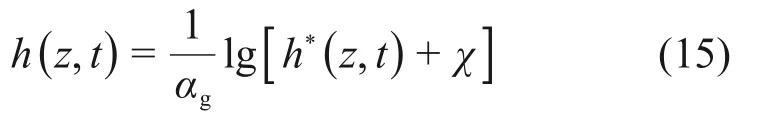
2 方法和改进
对于经典的线性方程组的矩阵分裂迭代法如Jacobi 迭代法、Gauss-Seidel 迭代法以及松弛型迭代法[31],矩阵A可分解为

式中:D为A的对角矩阵;U为A的上三角矩阵;L为A的下三角矩阵。Gauss-Seidel 迭代方法的迭代格式可表达为
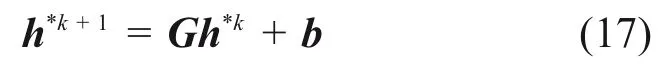
式中:迭代矩阵G=(D-L)-1U;b=(D-L)-1f;k为迭代次数。
为了进一步提高Gauss-Seidel 迭代法(GS)的收敛速度,引入松弛系数ω,定义ω为0~2,则迭代解可表达如下:
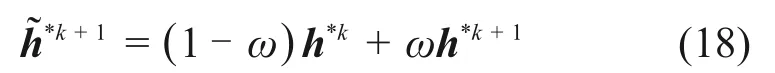
式中:uk+1表示为式(17)的迭代结果;因此,根据式(17)~(18)超松弛迭代法(SOR)的迭代格式可表示为
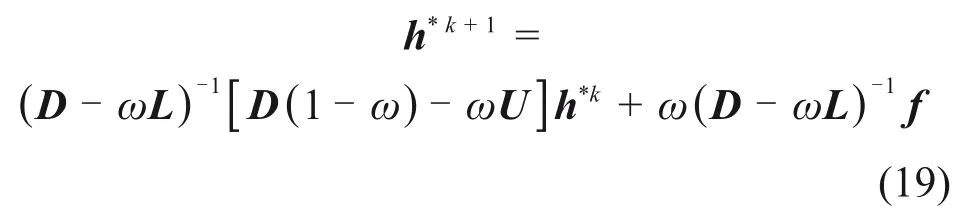
在式(19)中,ω的选择通常是困难的,没有一个通用的选取规则。因此,本文研究中采取迭代矩阵的最小谱半径来定义最佳ω,进而再进行迭代求解。式(19)的迭代矩阵为

不同的松弛系数ω可以从区间(0,2)中选取,其取值间隔为0.02,然后根据选取的ω计算对应的迭代矩阵谱半径,进而搜索最小谱半径位置,得到最佳松弛系数ω。将获得的ω代入迭代公式进行求解,在迭代求解过程中,当迭代满足时,则迭代停止,否则继续。
2.1 红黑排序的SOR迭代法(RB-SOR)
对离散节点重新编号,一种经典的排序方法(红黑排序)可将节点分裂为2个向量[31],奇数点(红点)为一组h*R,偶数点(黑点)为一组h*B,进而基于红黑分裂,离散后的线性方程组可表达为
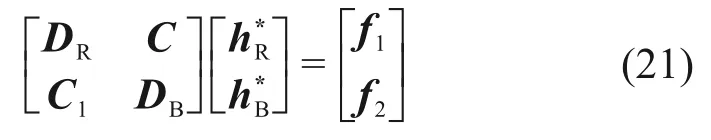
式中:DR和DB为对角矩阵,它们的元素个数分别为红和黑点数量。C和C1分别为与待求的黑、红点相关的交互矩阵。h*R和h*B分别对应红点和黑点的待求解向量;f1和f2分别为差分方程解算区域的边值和方程的已知项。用SOR 迭代方法求解线性方程组(21),有
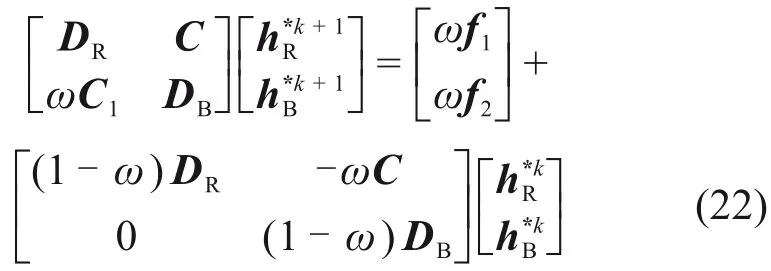
表达为
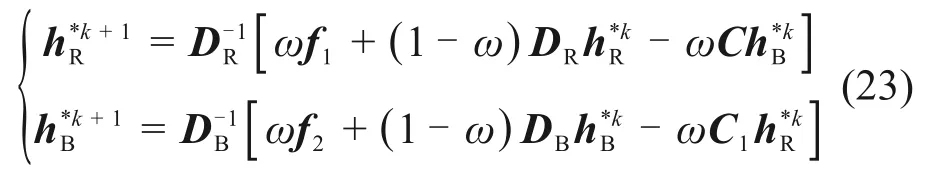
式(23)是红黑排序SOR 迭代一步的矩阵表达式,实际计算时也可不直接用这些矩阵公式,可结合式(18)更简便地获得红黑排序SOR 的数值解。具体地,先采用GS计算在红点的值,然后获得SOR的值:
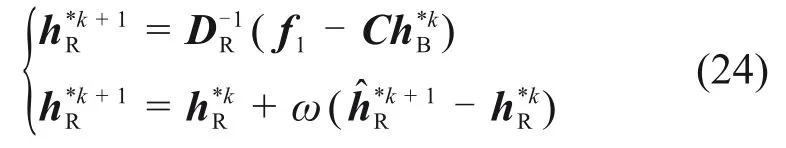
利用,再采用GS 计算在黑点的值,然后得到SOR值:

2.2 预处理SOR迭代法(P-SOR)
虽然SOR迭代法相比于GS迭代有了很大的改善,但SOR 的收敛速度仍需进一步提高。预处理技术被广泛地用于处理病态线性方程组问题并获得了较好的效果,寻求预处理子(M)应具有的性质[28]有如下几点:
1)M在某种意义下是矩阵A的较好近似;
2)M的构造所占用计算时间是非常小的,甚至可以被忽略;
3)预处理后的线性方程组比原方程组(式(14))的求解更容易。
因此,在研究中采用对角尺度化预处理子,这种预处理技术易于实施和计算,对称超松弛(SSOR)预处理子定义为

当用上述矩阵作为预处理子时,没有必要像迭代法那样去细致地选择参数ω。可取ω=1 即得对称Gauss-Seidel(SGS)预处理子,有
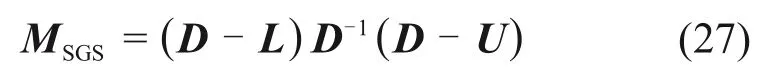
采用式(27)的预处理子对线性方程组(14)进行左预处理,有

对式(28)进行SOR迭代求解,获得相应的数值解,其迭代格式如下:
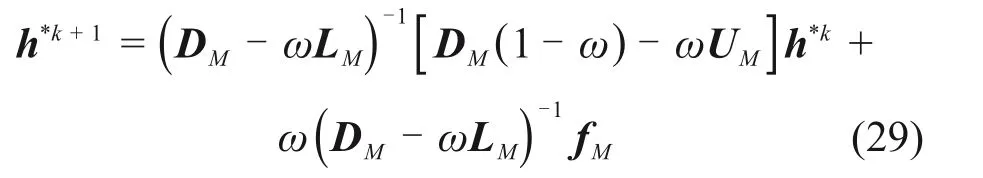
式中:DM,LM和UM为预处理后的矩阵;fM为预处理后的列向量。对于一个线性方程组Ax=b而言,可以采用条件数来评价给出的非奇异矩阵A是否病态,条件数定义如下[15]:

式中:矩阵范数‖ ‖为Frobenius范数。
综上,根据RB-SOR 和P-SOR 方法原理编写程序(MATLAB2014a)并计算求解,计算流程图如图1所示。
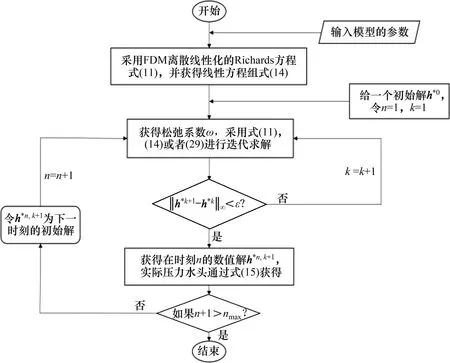
图1 RB-SOR和P-SOR迭代方法的计算流程图Fig.1 Calculating flow chart of RB-SOR and P-SOR iterative methods
为了验证提出方法的数值精度,采用均方根误差(Rh)进行比较,有

式中:和h*分别为分析解和数值解矩阵;j为节点数量;t为模拟时刻节点。为了更直观地比较P-SOR 的加速效果,加速比定义SGS/P-SOR为(以GS为例):

式中:TGS为采用GS 迭代法计算的CPU 时间;TP-SOR为采用P-SOR迭代法计算的CPU时间,其计算机的CPU为Intel i5-4590。
3 方法比较与验证
3.1 均质非饱和土的一维稳态数值解
第1个算例描述了均匀非饱和土中的一维稳态地下水渗流,数学模型如图2所示。

图2 一维降雨入渗模型Fig.2 One-dimensional model of rainfall infiltration
假定土体厚度L为10 m,则饱和含水量θs、残余含水量θr、土体的饱和渗透系数Ks和土的孔隙分布参数αg分别为0.35,0.14,1×10−4m/h 和8×10−3m−1[15]。上、下边界条件分别可描述为:


令干燥非饱和土的压力水头为hd=-1000 m,根据式(7),归一化的边界条件可写为:

对于一维均质非饱和土的稳态流问题,TRACY[21]提出稳态方程的解析表达式:
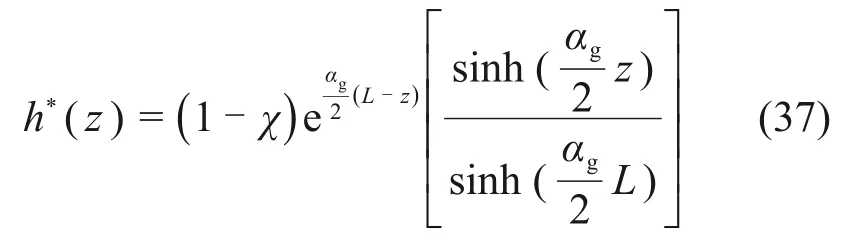
这个例子中收敛准则ε设置为10−8。
在不同的Δz下,分别采用GS,SOR、RB-SOR和P-SOR迭代法进行计算,结果如图3和表1所示,图3中:条件数是由矩阵A的范数乘积所表示,量纲为一,其数值越大,线性方程组的病态性越严重。由图3和表1可知:通过预处理技术处理后,原系数矩阵A的条件数大幅减小,至少减小了1个数量级。P-SOR方法迭代次数是最小的,GS迭代法的迭代次数最大,在数值上后者约为前者的100倍。

图3 不同网格大小下条件数的比较Fig.3 Comparison of condition number for different grid sizes
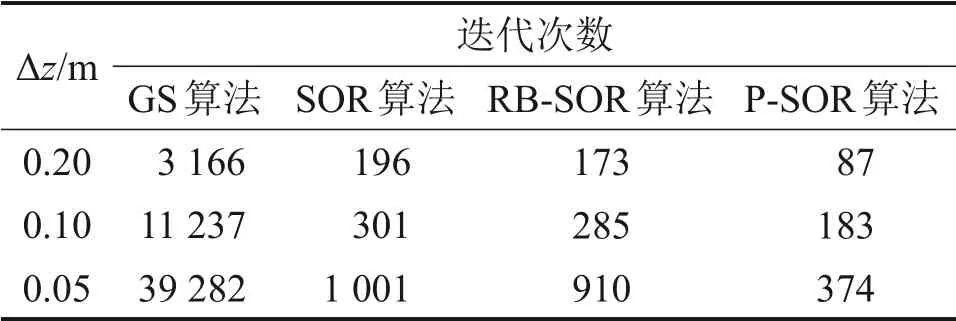
表1 求解稳态RE的数值结果Table 1 Numerical results for solving steady-state RE
图4所示为求解一维稳态方程不同方法的收敛率的比较结果(Δz=0.10 m)。由图4可见:GS 的收敛率最小;RB-SOR 的收敛率相较于SOR 有所提高,但提高幅度较小;P-SOR 的收敛率最快,并且相较于SOR有了更大提高。通过与解析解比较,上述4种迭代方法均有较高的精度,相对于解析解的绝对误差,GS 能达到10−6的数量级,SOR 达到10−8的数量级,P-SOR 和RB-SOR 均达到10−9的数量级。图5所示为一维稳态地下水流的数值解和解析解的比较。由图5可知:通过P-SOR法获得的压力水头与解析解十分吻合,当Δz分别为0.20,0.10和0.05 m时,其均方根误差分别为1.478×10−9,1.439×10−9和1.277×10−9,这说明改进的P-SOR 具有较高的数值精度和稳定性。
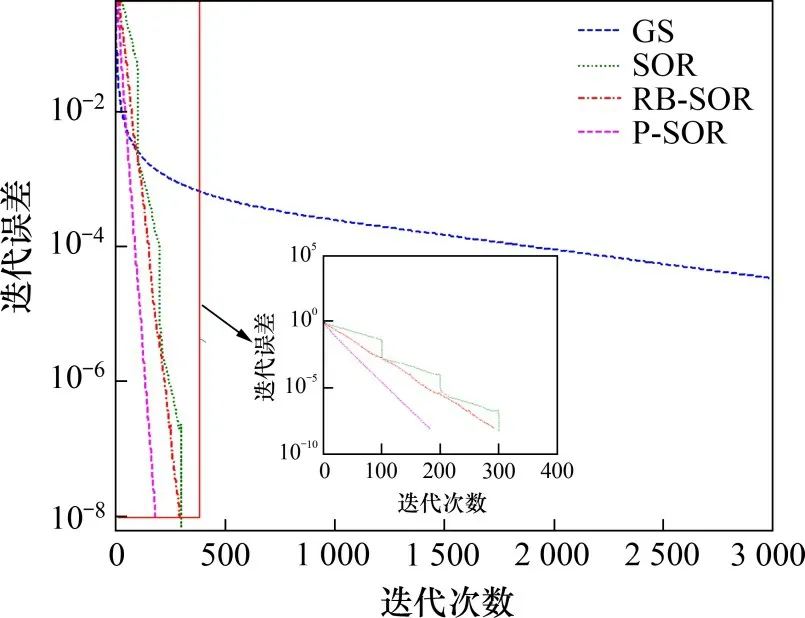
图4 求解一维稳态方程不同方法的收敛率的比较(Δz=0.10 m)Fig.4 Comparison of convergence rates of different methods for solving one-dimensional steady-state equation(Δz=0.10 m)

图5 一维稳态地下水流的数值解和解析解的比较Fig.5 Comparison of numerical and analytical solution for one-dimensional steady-state groundwater flow
3.2 均质非饱和土一维瞬态流数值解
第2个算例描述的是均质非饱和土的一维瞬态地下水渗流,数学模型依然如图2所示。除了非饱和土的孔隙大小分布参数αg=3.2×10-4m−1外,土体厚度L和其他模型参数与一维稳态模型是一致的。边界条件也与3.1节中描述的一致,初始条件为h(z,t=0)=-105m。对于均质非饱和土中的一维瞬态地下水渗流问题,TRACY提出的瞬态流解析解表达式如下[21]:

式中:λm=kπ/L;μm=α2g/4+λ2m;t为模拟时间。
总模拟时间设置为10 h,迭代方法的收敛标准ε设置为10−8。为了验证所提方法的计算效率和精度,网格长度取0.02,0.04和0.05 m,时间步长取为0.0100,0.0050和0.002 5 h。
图6所示为条件数随不同的Δt和Δz的变化,由图6可知:系数矩阵A与预处理后的系数矩阵M−1A的条件数随网格长度的减小而变大,随时间步长的减小而减小,然而,通过预处理方法,很好地降低了系数矩阵的条件数,可以看到M−1A的条件数均得到了大幅度减小,甚至接近1.0,这表明预处理过程能够有效地降低矩阵的病态性。

图6 条件数随不同的Δt和Δz的变化Fig.6 Change of condition number with different Δz and Δt
表2所示为4种不同迭代方法在不同的网格长度和时间步长条件下的迭代次数和计算时间。由表2可知:在不同网格长度和时间步长下,相比GS 和SOR,RB-SOR 和P-SOR 方法均能降低迭代次数和减少计算时间,而P-SOR的性能比RB-SOR的更好。图7所示为求解RE 不同方法的迭代次数和收敛率的比较结果(Δz=0.04 m)。由图7可知:在不同的Δt下,P-SOR表现出最少的迭代次数,RBSOR 迭代次数比GS 和SOR 的少;GS 的收敛率最慢,RB-SOR 和P-SOR 的收敛率相较于SOR 都有所提高,而P-SOR的收敛率最高。
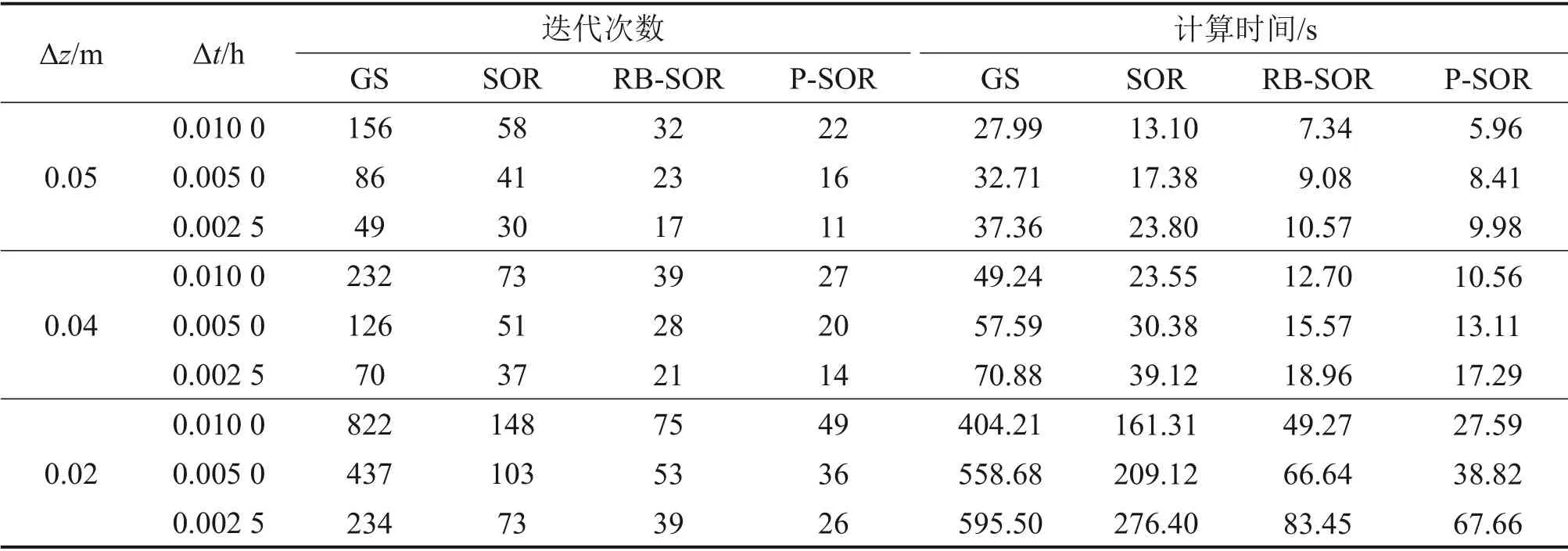
表2 求解瞬态流问题的数值结果Table 2 Numerical results for solving transient flow problem
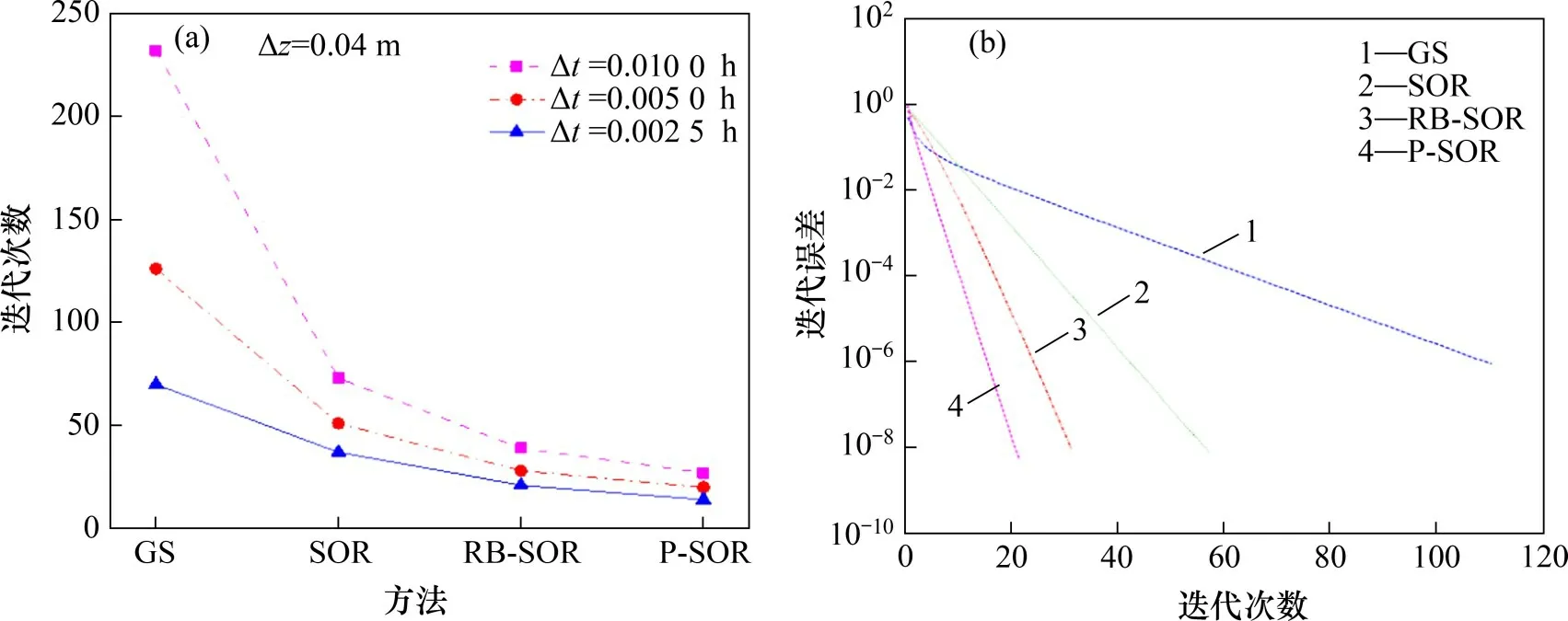
图7 求解RE不同方法的迭代次数和收敛率的比较(Δz=0.04 m)Fig.7 Comparison of iterations and convergence rates using different methods for solving RE(Δz=0.04 m)
图8所示为通过P-SOR获得的数值解和解析解的比较结果。由图8可知:由P-SOR方法获得的瞬态压力水头曲线与解析解十分吻合。图9所示为t=10 h时不同迭代方法在不同网格尺寸下的Rh。由图9可知:当t=10 h时,Rh达到了10−5数量级,同时,不同迭代方法的均方根误差随着网格尺寸的减小而减小。相较于SOR,P-SOR和RB-SOR的精度随着时间步长的减小都有小量提高。由于GS迭代法的均方根误差较改进的SOR迭代法大0.5~1个数量级,因此,此处并未纳入比较范围。结果表明,改进的SOR 方法均有较强的数值稳定性以及较高的计算精度(近似等价于SOR的精度)。

图8 通过P-SOR获得的数值解和解析解的比较Fig.8 Comparison of numerical solutions obtained by PSOR with analytical solutions
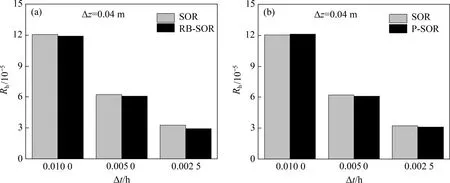
图9 t=10 h时不同迭代方法在不同网格的RhFig.9 Rh of different iterative methods at different grid length when t=10 h
图10所示为当Δt=0.005 h 时,P-SOR 和RBSOR 相对于GS 和SOR 的加速比,由图10可见:在不同的网格长度下,RB-SOR与P-SOR迭代法相对于GS 的加速比是最大的,SOR 的次之;当Δt=0.005 h 时,2 种改进方法相对于GS 的最小加速比分别为3.602 和3.891,相对于SOR 的最小加速比为1.914 和2.067。从数值结果来看,与于GS 和SOR相比,P-SOR与RB-SOR迭代法均表现出较高的计算效率,但是P-SOR 的加速效果比RB-SOR的加速效果好。

图10 比较不同改进的SOR相对于GS和SOR的加速比(Δt=0.005 h)Fig.10 Comparison sof speed-up ratios of different improved SOR relative to GS and SOR(Δt=0.005 h)
4 结论
1)在求解非饱和土一维降雨入渗问题时,与GS 和SOR 相比,2 种改进的SOR 方法均可提高进收敛率和提高数值精度。但P-SOR 比RB-SOR 具有更高的收敛率、更高的计算效率,这说明预处理技术相比较于矩阵分裂技术(红黑排序)具有更好的性能,可更大程度地提高收敛速度。
2)在离散RICHARDS 方程时,形成的系数矩阵A的条件数往往并不理想,尤其在稳态情况下条件数很大,因此,采用预处理技术有效减小系数矩阵A的条件数。在稳态情况下,系数矩阵的条件数减少了至少1个数量级,在瞬态情况下,条件数能够极大地减少,甚至接近于1.0。
3)基于这次研究对比,RB-SOR和P-SOR相比较于GS和SOR均有一定程度的加速效果,尤其在较细的网格条件下,2种改进方法的加速效果十分显著。相对于SOR,RB-SOR和P-SOR的加速比分别达43.93%和51.62%。因此,改进的SOR尤其是P-SOR在地下水渗流模拟中有广阔的应用前景。
