基于奇异值分解和均值聚类的单通道盲源分离算法研究

黄小青，肖 瑛，马艺伟

(大连民族大学 信息与通信工程学院，辽宁 大连 116605)

盲源分离是一种在源信号和混合矩阵未知的情况下，仅根据观测信号完成对源信号估计的一种技术，目前在地震信号处理、机械故障信号诊断、医学信号处理、语音信号处理等领域具有广泛的应用[1-2]。根据源信号和观测信号的数目，可将盲源分离问题分为：超定、正定和欠定盲源分离三类。当接收传感器小于源信号数目时，所得到的观测信号数目小于源信号数目，则该类盲源分离称为欠定盲源分离[3]，单通道信号盲源分离是欠定盲源分离的一个特例，也是盲源分离研究中的一个技术瓶颈问题。对于欠定盲源分离，目前主要的解决方法是结合数据分解技术的盲源分离和稀疏化盲源分离方法，结合数据分解技术如小波分解、经验模态分解等，通过维数扩展补充观测信号数目，使欠定盲源分离转换为正定盲源分离，并在此基础上利用独立分量分析等传统正定盲分离方法获得分离结果[4]。结合数据分解的盲源分离方法缺点是在无法确知源信号数目的情况下，扩展维数也无法确定，同时，不同的分解方法得到的在维数扩展中的虚拟通道上的观测信号质量有时会制约传统正定分离方法的性能。稀疏化盲源分离是利用观测信号的稀疏特征或观测信号在变换域中的稀疏特征，采用两步法进行源信号的估计[5]，即首先利用信号的稀疏特征对混合矩阵进行估计，对于欠定盲源分离，估计的混合矩阵的维数由观测信号数目和源信号的数目共同决定，无法直接求逆得到分离矩阵，此时在所估计的混合矩阵基础上利用线性规划方法来逐步进行源信号的估计。稀疏化盲源分离结果受混合矩阵估计精度的影响，同时当观测信号受到噪声污染时，分离性能不佳。

信号的传输过程中不可避免受到传输环境噪声的影响，为提高噪声干扰下单通道盲源分离性能，提出一种基于SVD分解均值聚类盲源分离算法。即对单通道观测信号进行SVD分解，利用中值准则对信号进行降噪处理，对保留的特征值分别进行分量恢复，将恢复的分量作为盲源分离观测信号。为了估计单通道信号中所包含源信号数目，对SVD分解分量作STFT进行稀疏化处理，在时频域中，根据各分量的散点图判别源信号的数目。对各分量时频域进行能量极小点剔除和单源点判定，利用K均值聚类方法估计混合矩阵，将估计的混合矩阵求逆即可得到对应的分离矩阵。算法将降噪、源信号数目判别和源信号恢复一并处理，适用于大多实际工程应用场合，计算机仿真结果证明了算法的有效性。

1 欠定盲源分离

盲源分离的简化数学模型可以表示为

X(t)=AS(t)。

(1)

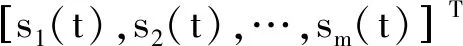
1.1 SVD分解

考虑实际工程中传感器采集的观测信号一般会受噪声干扰，在正定盲源分离的约束条件中，噪声可以被看作为一路源信号，并且在多路源信号中，最多只能有一路满足高斯分布的噪声，否则会降低源信号的分离性能，甚至导致分离方法失效。对于含有噪声的单通道观测信号，降噪是实现盲源分离的重要预处理工作。SVD降噪是利用信号与噪声的奇异值不同[6]，在奇异值分解后，可采用中值或者均值准则使对应于噪声分量的奇异值为零，然后重构原信号达到降噪的目的。对于给定的阶数为M×N的矩阵C，设有两个酉矩阵U∈RM×M和V∈RN×N，并且酉矩阵U和V同时满足UUT=I，VVT=I，并设

Λ=[diag{λ1,λ2,…,λp}]，

(2)

其中p=min(N,M)，使得式(3)成立，

A=UΛVT。

(3)

那么U和V则分别是M×M和N×N的正交矩阵，式(2)中Λ的对角元素称为奇异值，并且按照降序排列。因为Λ为对角矩阵，因此SVD可以将一个秩为K的M×N阶矩阵C表示成为K个秩为1的M×N阶子矩阵的和，每个子矩阵由两个特征向量和一个权值相乘得到，

(4)

式中：矢量ui和vi分别为矩阵U和V的第i列向量；λi是矩阵C的按降序排列的第i个奇异值。因此一个矩阵经过SVD分解，就成为一系列子矩阵Ci和相应的奇异值λi的乘积。SVD分解的实质是将矩阵投影到一系列不相关的子空间中，如果存在噪声，那么矩阵C经SVD分解得到的奇异值都不为零，即Λ为一个满秩的对角矩阵。对于单通道信号利用SVD分解，首先要对单通道信号进行相空间重构，即利用滑动窗对数据进行截断，构建Hankel矩阵，假设离散单通道观测信号为X(n)=[x(1),x(2),…,x(n)]，那么该离散信号的Hankel矩阵可以表示为

(5)

如果观测信号中存在噪声或者突发的干扰信息，那么Hankel矩阵可以写为

C=Cm+W。

(6)

式中：m=N-n+1；矩阵W可以看作是对矩阵C的一个扰动，对应了信号中的噪声部分；相对的Cm是信号的平滑部分在重构相空间的中的轨迹矩阵。根据奇异值对应信号和噪声的特点，利用SVD分解可以近似的获得Cm，即保留平滑信息对应的奇异值，将其他奇异值置零并利用式(4)重构原信号的方法实现降噪。如果在降噪的基础上，仅根据指定的奇异值利用SVD逆过程重构就可以得到SVD分解对应的不同分量，这些分量累加得到的信号就是降噪后的信号。利用SVD分解对应的分量作为观测信号，可以进行进一步的盲源分离工作。

1.2 混合矩阵估计

利用SVD分解得到的分量作为多路观测信号，实现了维数扩展，但是在未知源信号数目的情况下，仍然无法利用传统的独立分量分析(Independent Component Analysis，ICA)方法进行盲源分离。考虑式(1)模型中，如果源信号具有稀疏特征，即在大多数特定采样时刻，仅有一个源信号占优，而其他源信号在当前时刻可以近似为0。假设在采样时刻t占优的为第j个源信号sj(t)，那么满足系数特征的采样时刻式(1)可以写为

(7)

(8)

式(8)为一直线方程，该直线的方向与混合矩阵第j列向量方向相同，由此可知，如果源信号具有稀疏特征，那么观测信号则具有线性聚类特征[7]。

如果时域中源信号不满足稀疏特征，可以将时域信号转换到变换域获得满足稀疏特征后进行处理，常用的变换方法包括小波变换、傅立叶变换和时频变换。三个中心频率不同的正弦信号混合后选取其中两个观测信号的散点图如图1。可以看出在时域中散点图并不具有直线特征。文中采用STFT增强观测信号的稀疏性，根据式(1)得到对应的时频域盲源分离模型表示为

X(τ,f)=AS(τ,f)。

(9)

其中X(τ,f)和S(τ,f)分别对应时域观测信号X(t)和源信号S(t)的时频域表示。在时频域得到的观测信号的散点图如图2。可以看出时频域中源信号呈现典型的直线聚类特征。此外，根据时频域中的直线方向角数目可以判别出源信号的数目为3。

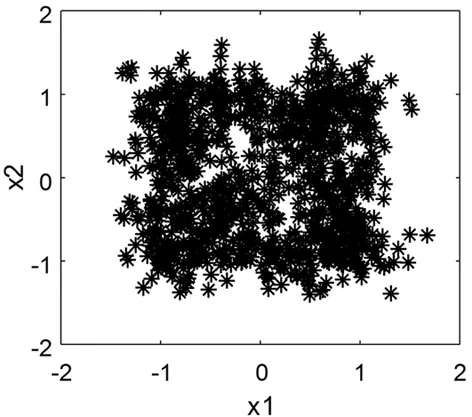
图1 时域观测信号散点图

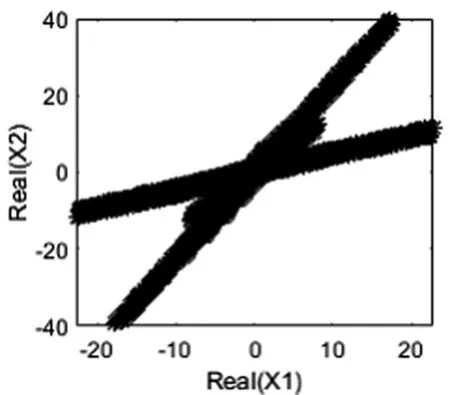
图2 时频域中观测信号散点图

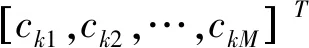
1.3 单通道盲源分离算法

由SVD和K-means均值聚类方法，这里给出一种单通道盲源分离算法。首先将单通道观测信号进行相空间重构，利用SVD分解，根据均值准则进行降噪处理，即

(10)

对于保留的奇异值λi分别根据SVD逆过程重构对应的分量，即

(11)

(12)

利用M1剔除能量极小值，

(13)

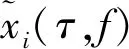
(14)

式(14)可以直接由式(8)推导得到，可见如果时频点(τi,fi)为单源点，那么对应在该时频点上的任意两个不同观测信号的比值为实数。但是实际中由于STFT变换中加窗的能量泄露以及噪声干扰等因素，这一比值严格为实数的概率很小，仅需要其虚部足够小即可，设

(15)

(16)

其中ξ为设定的较小的判决阈值，则单源点则可以根据M2与相应观测信号的时频表示点乘来获得。

(17)

完成能量极小点剔除和单源点检测可以在时频平面内去除影响聚类精度的大量无用样本数据，使得观测信号的线性聚类特征更为明显。

对完成预处理后的观测信号进行K-Means聚类，得到估计混合矩阵，并利用矩阵求逆获得分离矩阵，以观测信号和分离矩阵相乘获得源信号的估计。

2 仿真实验

仿真中利用正弦信号与方波信号和一路高斯噪声信号模拟源信号，其中采样频率为1024 Hz，正弦信号和方波信号的中心频率分别为15 Hz和5 Hz，混合矩阵为

(18)

观测信号的波形如图3。

a)观测信号1

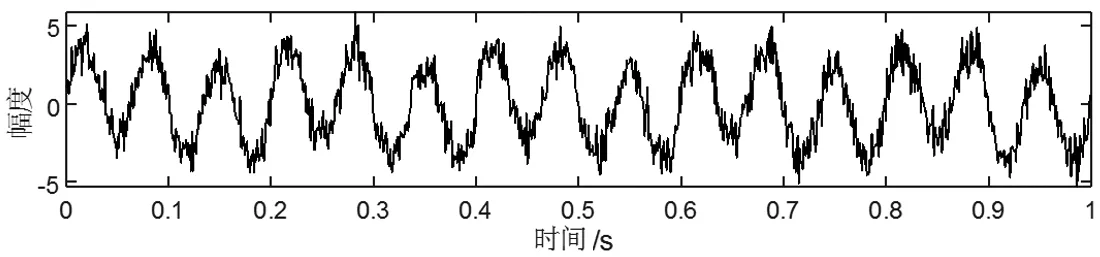
b)观测信号2

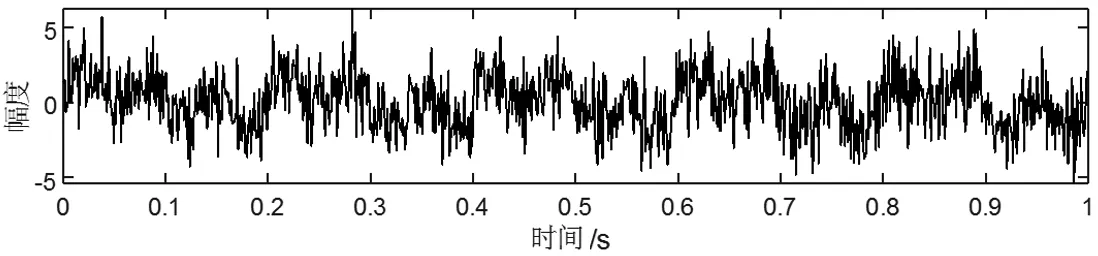
c)观测信号3

以第一路观测信号模拟单通道混合信号，并对其进行SVD分解，在SVD分解结果中利用均值准则去除噪声分量，并保留前两个奇异值分别重构分解分量作为新的观测信号。SVD分解得到的奇异值如图4，采用均值准则进行降噪处理则只保留前两个奇异值，分别以前两个奇异值进行分量重构，对两个分量进行STFT变换，并进行能量极小值剔除和单源点检测后绘制的散点图如图5，由图5可确定源的数目为2。进行K-Means均值聚类估计混合矩阵，并以混合矩阵的逆求得分

离矩阵，利用SVD重构的两个分量乘以分离矩阵得到源信号的估计结果如图6。从图6中可以看出，方波信号和正弦信号得到了有效分离。

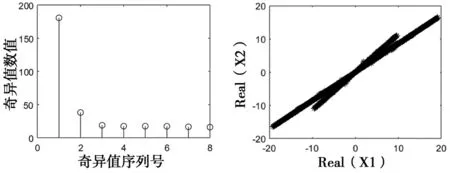
图4 SVD分解奇异值 图5 预处理后散点图

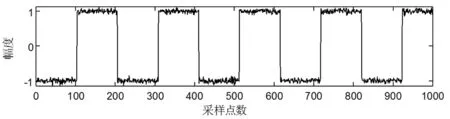
a)分离信号1

b)分离信号2

3 结 语

文中提出了一种基于SVD分解和K-Means聚类的单通道盲源分离算法，将SVD降噪与K-Means聚类估计混合矩阵进行了结合，在利用SVD降噪的同时，分别以保留的不同奇异值构建分量作为观测信号，实现了观测信号的维度扩展。利用STFT对信号进行稀疏化处理，在时频域中通过能量极小值剔除和单源点检测后的观测分量散点图估计源信号数目。利用K-Means均值聚类在观测信号时频域基础上获得混合矩阵的估计，得到源信号的恢复。算法在对工程上具有噪声干扰条件下的单通道信号处理中具有实际应用价值。