基于多元线性回归对调剖非均质储层分流率影响因素分析

李建晔，杨 喜，鞠 野，李 翔，徐国瑞，杨劲舟，刘光普

(1.中海油田服务股份有限公司油田生产事业部，天津 300459；2.中海石油(中国)有限公司天津分公司，天津 300459)

渤海油田储层以砂岩和碳酸盐岩为主，部分油田具有胶结疏松、储层非均质性严重、平均渗透率较高的特点[1]，其渗透率与陆地油田相比平均高出1～2个数量级，因此海上油田低渗透层的启动压力很低，一般高于注入压力，因此在笼统调剖剂注入时，对于非均质储层无法通过低渗层的启动压力来判断是否有药剂侵入[2-3]。引入高渗层分流率作为非目的层是否污染的标准，当高渗层的分流率低于100%时，可以判定为中低渗层污染。为了避免部分调剖剂进入非目的层，影响调剖效果，笔者以三管并联岩心模型实验为基础，以数学软件分析为辅助，对笼统调剖过程中非均质储层分流率影响因素进行分析[4-7]。

1 实验部分

1.1 实验材料

聚合物为部分水解聚丙烯酰胺，相对分子质量为1 900×104，固含量为88%，大庆炼化公司生产；酚醛交联剂、促胶剂、固化剂，大学实验室生产；矿化度调节剂NaCl、CaCl2、NaHCO3、Na2SO4、KCl、MgCl2、Na2CO3，天津市大茂化学试剂厂生产；实验用油为模拟油，由A油田脱气原油与煤油按一定比例混合而成(μo=15 mPa·s)；实验用水为模拟注入水(简称注入水)，是按照A油田注入水水质分析结果于室内配制而成，结果如表1所示。

表1 水质分析结果

实验模型由高中低3种渗透率人造均质岩心并联而成，单块岩心外观几何尺寸为：高×宽×长=4.5 cm×4.5 cm×30 cm，渗透率Kg分别为6 000×10-3、1 500×10-3μm2和500×10-3μm2。

1.2 仪器设备

利用DV-Ⅱ型布氏黏度仪(博勒飞公司生产)测试调剖剂黏度；岩心驱替实验装置由平流泵、压力传感器、岩心夹持器、中间容器等部件组成，除平流泵外，其他部分置于65 ℃保温箱内。该实验设备由海安县石油科技仪器有限公司生产，实验设备和流程如图1所示。

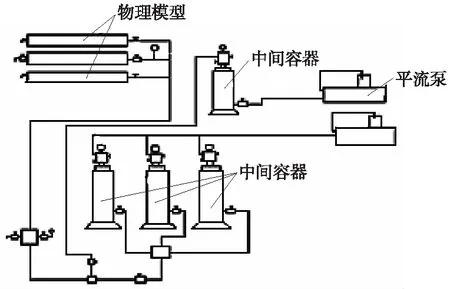
图1 实验设备及流程Fig.1 Schematic diagram of laboratory equipment and processes

1.3 实验方案

(1) 饱和水并测量每一块岩心的渗透率；

(2)饱和油并进行第1次水驱，水驱至含水98%；

(3)连续注入3PV的调剖剂(聚合物+交联剂+促胶剂+固化剂=3 000+3 500+1 200+2 000 μL/L)，记录注入过程中各岩心夹持器的产液情况以及岩心夹持器上面的压力变化情况；

(4)重复3次上述实验。

1.4 实验结果

1.4.1 岩心数据

岩心数据如表2所示。

1.4.2 分流率与其相关因素的关系

分流率与其相关因素的关系分别如图2～图5所示。

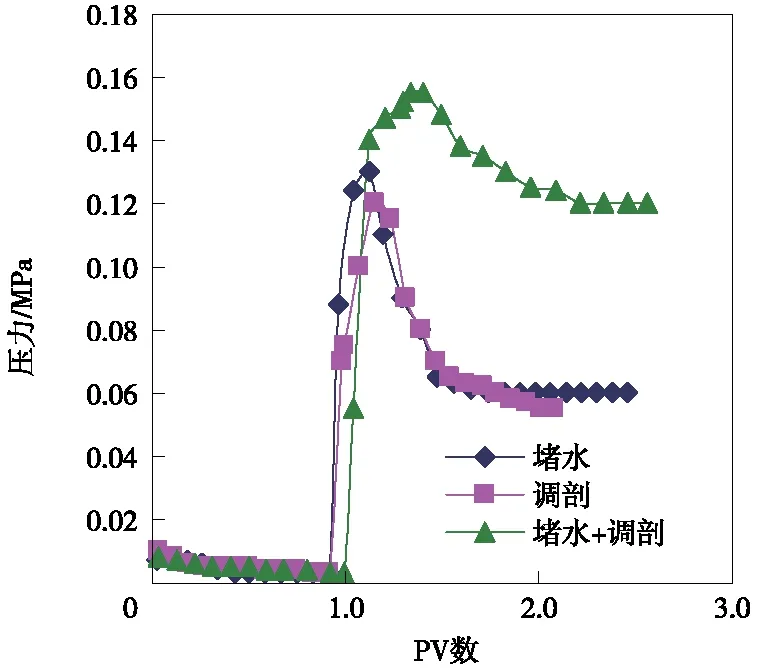
图2 注入压力与PV数关系Fig.2 Injection pressure versus PV number

图3 PV数与分流率的关系(方案1)Fig.3 Relationship between PV number and diversion rate (Scheme 1)

图4 PV数与分流率的关系(方案2)Fig.4 Relationship between PV number and diversion rate (Scheme 2)

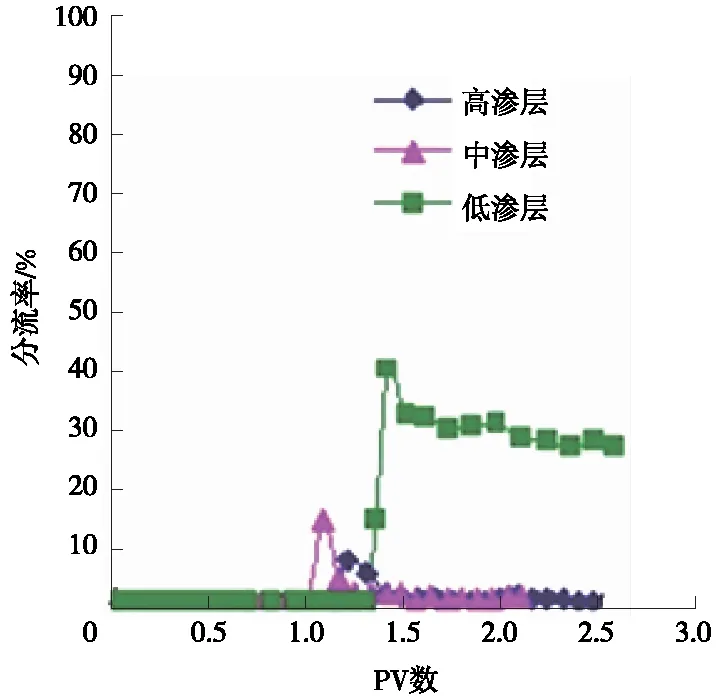
图5 PV与分流率的关系(中渗层)Fig.5 Diversion rate versus PV number (mesocosm)

从图2～图5中可以看出，注入压力、PV数、渗透率都与分流率有关，注入压力越大，高渗层渗透率越小，注入PV数越大，中低渗层越容易“污染”，但是其中的线性关系以及相关性、影响的重要程度没有办法通过实验得出。对于一元线性回归分析，因为无法判定哪些因素是主要的、起决定性作用，哪些因素是次要的，所以无法利用一元线性回归进行分析。因此，多元线性回归、SPSS软件并借助计算预测了多个自变量的最优组合[8]。

2 多元线性回归分析

2.1 数据来源及模型假设

模型中的数据来源于实验室的岩心实验，所用的油为A油田油井采出油，水为A油田模拟水，实验药剂为实验室研发，为便于解决问题，特提出以下假设：

(1)假设暂不考虑其他因素对高渗层分流率的影响；

(2)假设室内实验药剂具有普遍性，能够代表一般调剖剂的实验效果；

(3)假设实验室所配置的模拟水能够代表现场水质的实际水平；

(4)假设非均质岩心能够代表现场实际近井地带的水平。

2.2 模型构建

将岩心高渗层渗透率、中渗层渗透率、低渗层渗透率、注入压力、PV数、分流率6个指标的数据导入SPSS软件进行分析，将分流率选为因变量，其余参数选为自变量，并进行建模。

设系统变量y与k个自变量x1，x2，…，xk之间存在统计线性相关关系，且可表示为：

Y=a0+a1x1+a2x2+…+akxk

给定n组样品数据点如下：(y1，x11，x21，…，xk1)，(y2，x12，x22，…，xk2)，…，(yn，x1n，x2n，…，xkn)。

则满足：

Yi=a0+a1x1i+a2x2i+…+akxki+

ε(i=1，…，n)

设εi～N(0，σ)(I=1，…，n)，那么可由最小二乘法获得多元线性回归模型[9]：

Y=a0+a1x1+a2x2+…+akxk

2.3 模型拟合度及线性关系分析

2.3.1 参数相关性分析

运行得出的模型汇总表如表3所示。

表3 德宾-沃森检验

德宾-沃森检验简称D-W检验，是目前检验自相关性最常用的方法，但其只适用于检验一阶自相关性[10]。由表3得知，该模型的DW值为0.367，接近于0，存在一阶相关性，但是其参数的线性关系无法利用德宾-沃森进行检验，因此接下来进行方差分析。

2.3.2 模型方差分析

模型方差分析结果如表4所示。

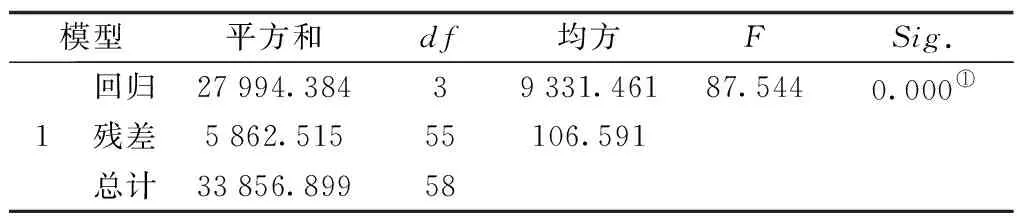
表4 模型方差分析

从表4中可以看出，模型1中的回归平方和为27 994.384，残差平方和为5 862.515，由于总平方和=回归平方和+残差平方和，由于残差平方和(即指随机误差，不可解释的误差)约等于回归平方和的20%，所以，此线性回归模型解释了总平方和的80%，根据F统计量的概率值为0.000，由于0.000<0.01，随着自变量的引入，其显著性概率值均远小于0.01，所以可以显著地拒绝总体回归系数为0的原假设，通过表4方差分析可以看出，自变量与因变量之间存在着线性关系，至于线性关系的强弱，需要进一步进行分析。

2.3.3 模型无关因素排除

已排除的变量如表5所示。

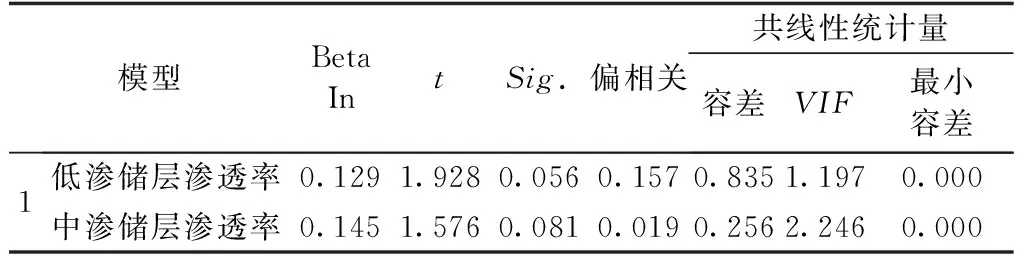
表5 已排除的变量①

从表5中可以看出，模型1中各变量中的T检的概率值都大于0.05，所以不能够引入线性回归模型必须剔除。因此结合实验情况可以得到一个结论，即非均质储层分流率与中低渗层的渗透率无关。

2.3.4 多元线性回归方程

多元线性回归方程系数如表6所示。

表6 多元线性回归方程系数

从表6中可以看出，多元线性回归方程为：

y=-5 031.388-38.672x1+2.056x2+0.223x3

由于注入常数项的sig为0.401>0.1，所以注入常数项不具备显著性，所以在标准系数中，常数项没有数值，已经被剔除。所以，标准化的回归方程为:

y=-38.672×x1+2.056×x2+0.223×x3

式中：y=高渗层分流率，%；x1=注入压力梯度，MPa/m；x2=注入pv数，无量纲；x3=高渗层渗透率，mD。

2.3.5 模型准确性验证

(1) 共线性诊断

多重共线性是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。一般来说，由于经济数据的限制使得模型设计不当，导致设计矩阵中解释变量间存在普遍的相关关系，如表7所示。

从表7中可以看出，从自变量相关系数矩阵出发，计算得到4个特征值，最大特征值为4.877，最小特征值为0.210。

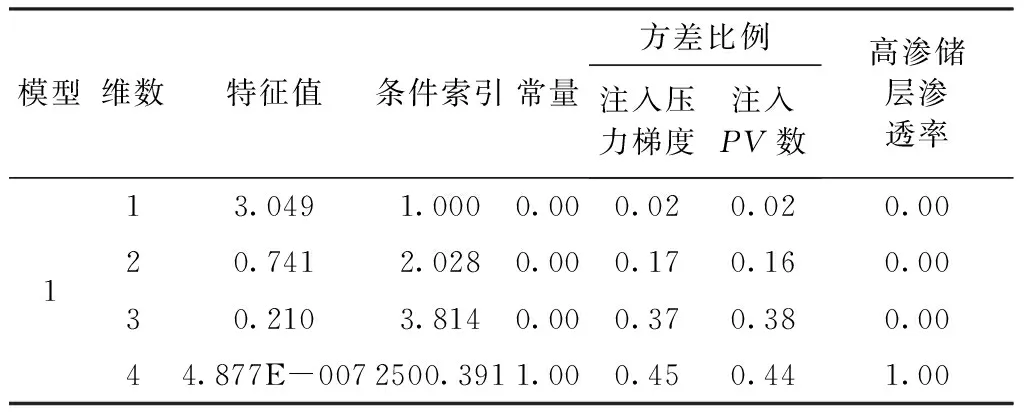
表7 共线性诊断

标准化后，方差为1，每一个特征值都能够刻画自变量的一定比例，所有的特征值能够刻画某自变量信息的全部，于是可以得到以下结论：

①注入压力梯度在方差标准化后，第1个特征值解释了其方差的0.02，第2个特征值解释了0.17，第3个特征值解释了0.37，第4个特征值解释了0.45。

②注入PV数的第1个特征值解释了其方差的0.02，第2个特征值解释了0.16，第3个特征值解释了0.38，第4个特征值解释了0.44。

③高渗储层渗透率的第1个特征值解释了其方差的0.00，第2个特征值解释了0.00，第3个特征值解释了0.00，第4个特征值解释了1.00。

注入压力梯度和注入PV数之间不存在共线性，或者共线性关系较弱，而高渗储层渗透率与注入压力梯度和注入PV数存在一定程度上的共线性，即近似共线性。由于多重共线性是普遍存在的，轻微的多重共线性问题可不采取措施，由于模型仅用于预测且拟合程度较好，因此不处理多重共线性问题，不影响预测结果。

(2)残差分析

残差分析就是通过残差所提供的信息分析出数据的可靠性、周期性或其他干扰 ，用于分析模型的假定正确与否。标准化残差的标准P-P图如图6所示。

从图6中可以看出，期望的积累概率在观测的积累概率附近。可以解释大部分的预测值，因此该模型线性关系成立。

图6 标准化残差的标准P-P图Fig.6 Standard P-P plot of standardized residuals

3 矿场应用

3.1 设计情况

渤海某油田A井，经油藏分析该井Nm0+I层存在高窜流强度渗流通道，NmII层主要存在平面矛盾，因此进行笼统调剖设计，实现优势渗流通道封堵，改变油藏深部液流方向，扩大水驱波及体积。该井注入过程中为避免非目的层污染，根据设计用量以及注入速度，利用方程计算，结果为在注入过程中注入调剖药剂升压压力小于4 MPa。

3.2 施工情况

该井于2019年施工，施工周期34 d，注入药剂浓度按照设计要求，注入过程中一直控制注入压力的上升，压力实现缓慢的上升，如图7所示。

图7 Nm 0+I+II油层施工曲线Fig.7 Nm 0+I+II oil formation construction curve

由图7中可以看出，药剂最后1个段塞注入压力稳定在5.3～5.9 MPa，整个施工周期注入药剂升压压力为3.3 MPa，小于设计4 MPa，避免了储层的污染。

3.3 见效情况

开井生产后，对应受效油井，含水和增油量均有大幅度的改善，截止到2020年7月，该井组累计递减增油6 136 m3，平均日增油66 m3，平均降低含水率为17%，现已取得了良好的稳油控水效果。措施效果统计如表8所示，井组注采曲线如图8所示。

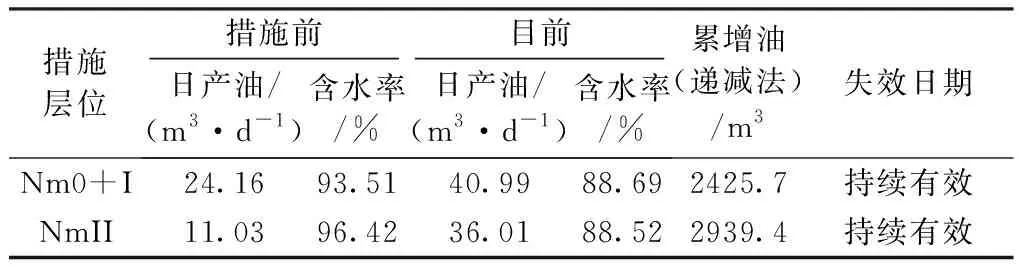
表8 措施效果统计

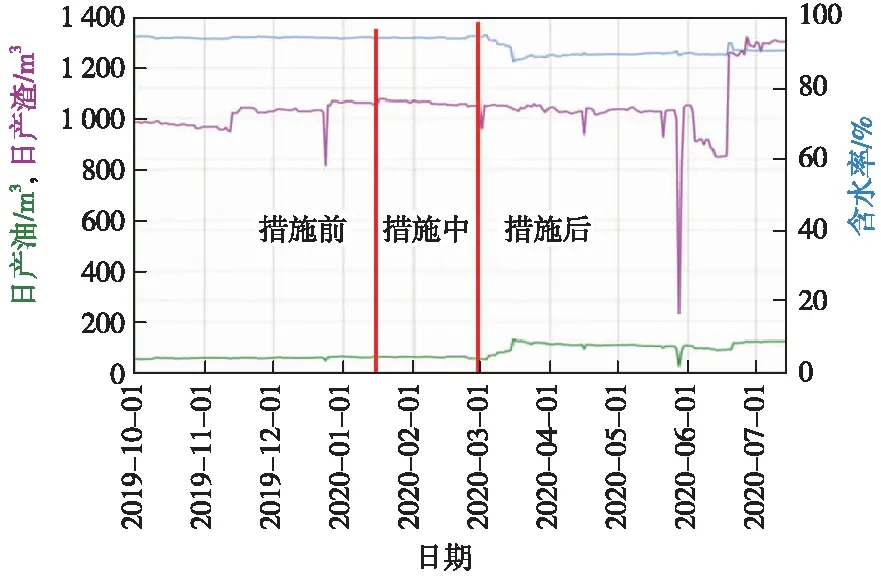
图8 井组注采曲线Fig.8 Well group injection and recovery curve

4 结论

(1)在调剖剂笼统注入过程中，非均质储层分流率与中低渗层的渗透率无关。

(2)在调剖剂笼统注入过程中，非均质储层分流率与高渗层的渗透率、注入压力、注入PV数有关，其中与高渗层的渗透率相关性最大。

(3)利用SPSS软件建立多元线性标准化的回归方程为：y=-38.672×x1+2.056×x2+0.223×x3。

(4)经过现场实际应用，避免了笼统调剖对非目的层的污染，该方程对现场施工具有一定的指导意义。