岩石广义流变柔量、模量时间依存性

张海龙，汤 杨，任 汀，大久保诚介

(1.重庆文理学院 土木工程学院，重庆 402160；2.中国建筑第七工程局有限公司，河南 郑州 450004；3.重庆三峡学院 土木工程学院，重庆 404000)

岩石的蠕变和应力松弛特性呈现出明显的时间依存性[1–2]，两种流变特性与长期强度直接影响到地下工程的稳定性和安全性[3–4]。然而，很多深部岩体工程中，岩体既不是纯蠕变，也不是纯应力松弛，而是随着时间的增加，应力和应变同时发生变化，表现出时间依存性，导致岩体最终破坏，这种现象用一般的蠕变和应力松弛很难解释清楚[5]。Fukui等[6]把应力和应变同时发生变化的这种现象称为广义应力松弛。Okubo等[7]利用非线性黏弹性模型对三城目安山岩广义应力松弛试验结果进行了数值计算。张海龙等[5]基于Maxwell模型的可变模量本构方程对河津凝灰岩广义应力松弛试验进行了数值模拟，并系统介绍了单轴压缩荷载下广义应力松弛的工程物理意义。张海龙[8]将随着时间的增加，应力和应变同时发生变化的这种现象称为广义流变。广义流变试验需要能够长期准确控制应力和应变信号，且通过以应力和应变的组合作为反馈信号（应力归还控制）的伺服试验机来实现。张海龙等[9]利用变阻器技术实现了应力归还控制，并执行了不同岩石的广义流变试验，对不同条件下的广义流变时效特性进行了深入研究。许江等[10]执行了不同围压条件下的广义流变试验，结果显示广义流变具有明显的围压影响效应。

蠕变和应力松弛是岩石材料固有的时效特性，与岩石工程长期稳定性密切相关[2,11–12]。流变过程中会导致材料损伤不断发展，使岩石整体强度下降。大型岩体工程施工中，由于区域地应力水平较高，工程施工期及运行期围岩流变现象可能显著影响工程施工安全及长期稳定性[13–16]。蠕变和应力松弛是广义流变的两种特殊形式，蠕变柔量和松弛模量是广义流变的重要特性，在线性黏弹性理论中，明确了蠕变柔量与松弛模量的一般实用表达式[17–19]。黄文柯[20]、刘军虎[21]、阳建红[22]等针对沥青混合料蠕变试验结果，采用拟合的方法得到蠕变柔量与松弛模量之间的转换关系。Sun等[23]通过三点弯曲蠕变试验计算了高黏度沥青砂的松弛模量。Kassem等[24]通过有限元法计算了火箭弹药柱蠕变柔量和松弛模量的表达式，得到蠕变柔量和松弛模量变异系数在同一量级上。

综上所述，蠕变柔量由蠕变试验获得，松弛模量由应力松弛试验获得，在线性黏弹性理论中，两者之间可相互转换，没有本质的区别[25]；但在岩石的非线性黏弹性行为中，两者关系还不明确，由应力归还控制实现的广义流变为研究两者关系提供了可能，本文通过引入广义流变理论研究两者关系，从而揭示岩石非线性流变的广义属性。

1 试验方法

Wawersik等[26]把岩石分为Ⅰ类和Ⅱ类岩石，Ⅰ类岩石峰后破坏曲线缓慢下降，呈延性破坏；Ⅱ类岩石峰后破坏曲线急剧下降，呈脆裂破坏。本文选择Ⅰ类岩石（田下凝灰岩）和Ⅱ类岩石（三城目安山岩）进行广义流变试验，这两种岩石都来自于日本，田下凝灰岩广义流变试验在重庆大学完成，三城目安山岩广义流变试验在日本东京大学完成。试验由应力归还控制的伺服试验机执行，控制方式如图1所示，应力归还控制把应力和应变的线性组合作为控制变量反馈给伺服阀[5]，控制公式为：

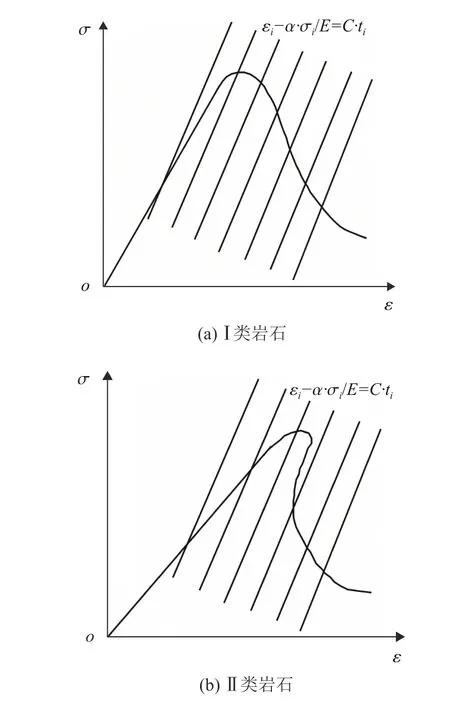
图1 应力归还控制法示意图Fig. 1 Schematic diagram of stress-feedback controlling method

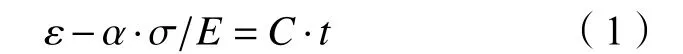
若仅考虑将应变信号反馈给伺服阀，则可令σ＝0，即为应变速率控制，如式（2）所示：

若仅考虑将应力信号反馈给伺服阀，则可令ε=0，即为应力速率控制，如式（3）所示：

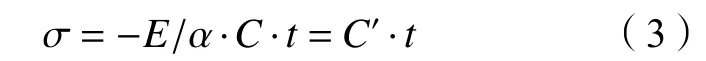
可见，应变速率控制和应力速率控制是应力归还控制的两种特殊形式[9]。

试件尺寸为直径25 mm、高50 mm，端面磨平度为0.01 mm。试验前，将所有试件放置在真空恒温箱里烘干2周，两种岩石基本力学参数如表1所示。预施加1%的荷载使试件固定在试验机上、下压头之间，并以C= 1×10–5/s的加载速率从原点开始加载至广义流变启动点SPT（starting point）后，停止加载。田下凝灰岩SPT为50%、80%，三城目安山岩SPT为50%、65%、80%，伺服试验机根据预设的广义流变方向系数α（3.0、±∞、–3.0、–1.0、–0.3、0、0.3）执行广义流变试验，从启动点开始到试验结束或者试件破坏的时间称为广义流变时间，广义流变原理如图2所示。

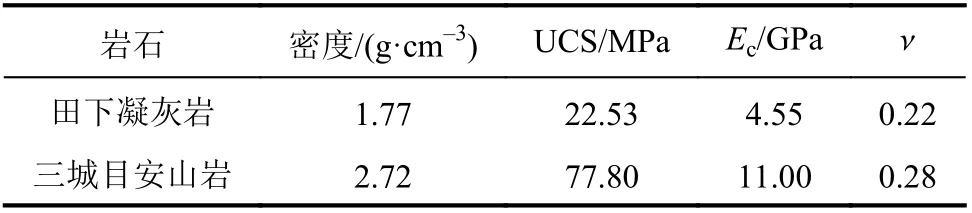
表1 两种岩石基本力学参数Tab. 1 Basic mechanical parameters for two rocks

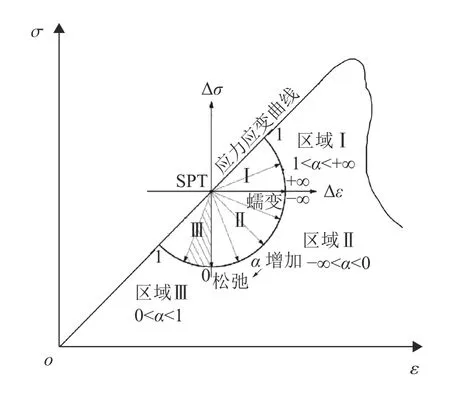
图2 岩石广义流变原理Fig. 2 Generalized rheological principle for rocks

图2中，以SPT为圆点构成的四象限中，不同的α值将广义流变划分为一个半圆，此半圆沿着顺时针方向可分为3个区：第1象限（区域Ⅰ），1 ＜α＜+∞；第4象限（区域Ⅱ）， −∞＜α＜0；第3象限（区域Ⅲ），0＜α＜1。 蠕变试验（ α =±∞）从启动点开始沿水平轴向右延伸，松弛试验（ α=0）从启动点开始沿垂直轴向下延伸。

可见，蠕变和松弛是广义流变的两种特殊形式，广义流变能够全面描述工程时间中的流变现象。

从哪儿入手？服务国家重点建设项目去！化建公司的决策者果断地做出了进军扬子乙烯的战略决策。扬子石化建设项目是国家“六五”“七五”期间的重点建设项目，工程总投资达66.84亿元。这一步是化建公司有史以来第一次积极主动参与市场竞争。在新的建筑市场，通过保安全、保质量、保工期，化建公司作为“特别能干活的西北牛”赢得了新的荣誉，树立了新的形象。

2 广义流变试验结果及分析

2.1 广义流变试验结果

选择50%启动点的田下凝灰岩和三城目安山岩的试验结果分析广义流变特性，如图3所示。

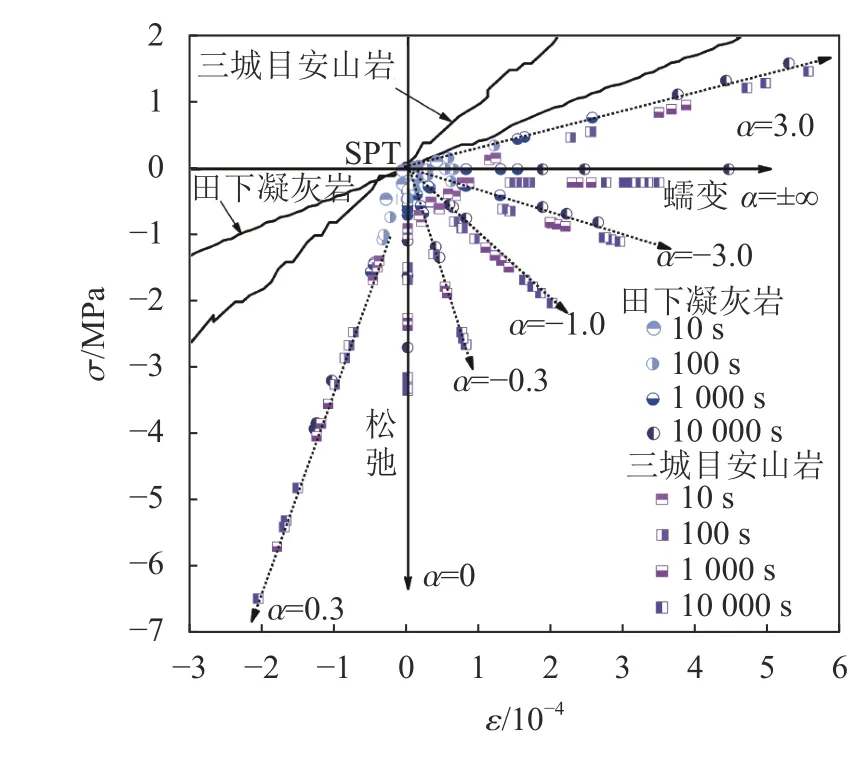
图3 两种岩石50%应力水平广义流变特性（SPT归零）Fig. 3 Generalized rheological behaviors for two rocks at 50% stress level (SPT return zero)

图3中：把原点、横轴和纵轴平移到归零后的启动点SPT处，两条实线分别为田下凝灰岩和三城目安山岩的全应力–应变曲线；圆点、正方形点分别为田下凝灰岩、三城目安山岩在第10、100、1 000、10 000 s这4个时刻的广义流变位置；虚线箭头是广义流变方向（即不同α值），与图1中应力归还控制线的斜率方向一致。由图3可知：同一流变时刻，三城目安山岩的应力和应变的变化值大于田下凝灰岩；同一α下，两种岩石广义流变方向基本一致，其广义流变曲线具有相似性，广义流变试验结果与图2中的原理所述一致。从而可知，Ⅰ类和Ⅱ类岩石广义流变具有相同的时间依存性。

2.2 广义流变柔量、模量

线弹性材料中，材料变形破坏过程中的应变与应力的比值称为柔量，在恒定应力条件下，蠕变应变和蠕变应力水平的比值称为蠕变柔量Gcreep−comp(t)；与蠕变柔量相对应，松弛应力和松弛应变水平的比值称为松弛模量Grelax−modu(t)，具体定义为[21]：

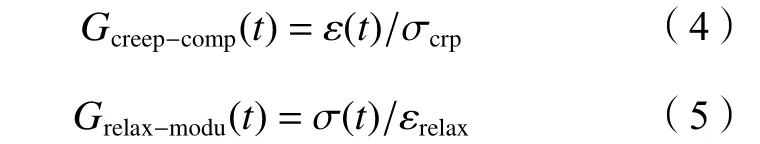
式中， ε(t) 为 蠕变应变， σcrp为蠕变应力水平， σ (t)为松弛应力， εrelax为松弛应变水平。由式（4）和（5）可知，线弹性材料的蠕变柔量Gcreep−comp(t)和松弛模量Grelax−modu(t) 互 为 反 比 例 关 系，即Gcreep−comp(t)∝1/Grelax−modu(t)，呈线性流变特征。在非线性黏弹性材料中，基于式（4）和（5），本文定义式（6）和（7）为广义流变柔量Gc(t)和模量Gm(t)，如图4所示。

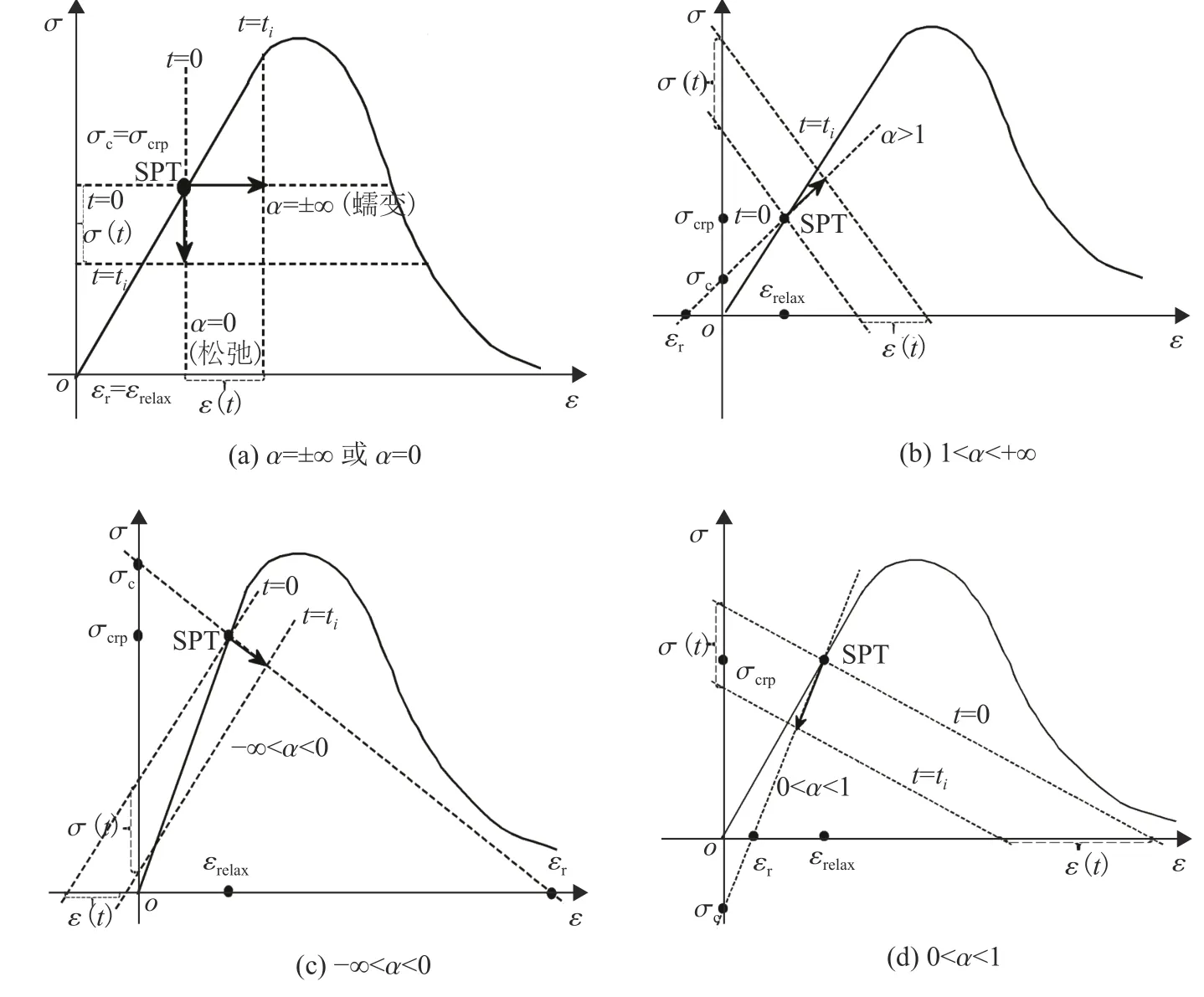
图4 岩石广义流变柔量、模量Fig. 4 Generalized rheological-compliance and modulus of rocks

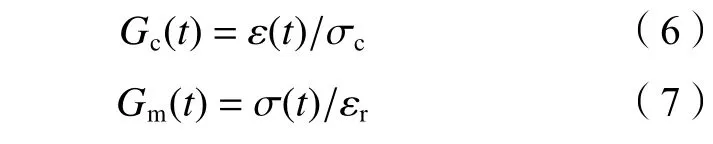
式中： ε(t)为 广义流变时间t=0 和t=ti时刻等时线应变的差值； σ(t)为 广义流变时间t=0 和t=ti时刻等时线应力的差值；在方向系数α条件下，广义流变曲线延长线相交横轴为εr点 ，相交纵轴为σc点，分别称为广义关联应变和广义关联应力。

式（6）和（7）有如下4种情况：

1）蠕变（α =±∞） 和松弛（α =0）：蠕变柔量和松弛模量计算如图4（a）所示。如果是松弛条件，则 εr=εrelax；如果是蠕变条件，则σc=σcrp。计算方法和式（4）和（5）相同。

2）区域Ⅰ（1 ＜α＜+∞）：广义流变柔量和模量计算如图4（b）所示。εr为负值，且随着α顺时针方向增大，εr减小；σc总为正值，且随着α顺时针方向增大，σc增大，具体如式（8）、（9）所示：

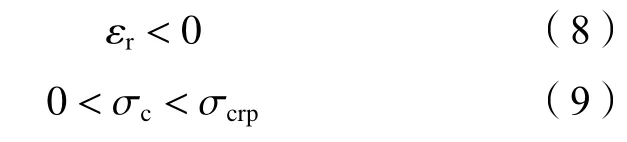
3）区域Ⅱ（ −∞＜α＜0）：广义流变柔量和模量计算如图4（c）所示。εr和σc为正值，且随着α顺时针方向增大，εr减 小，σc增大，具体如式（10）、（11）所示：

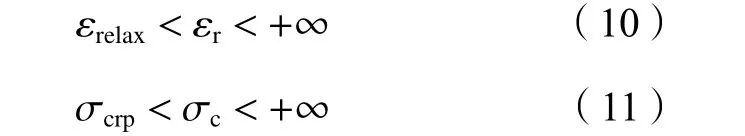
4）区域Ⅲ（ 0 ＜α＜1）：广义流变柔量和模量计算见图4（d）。εr为 正值，σc总为负值，且随着α顺时针方向增大，εr减 小，σc增大，具体如式（12）、（13）所示：

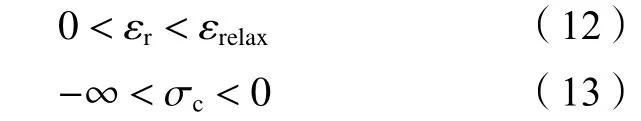
综上所述，εr和 σc的定义方法包含了蠕变和松弛现象，与广义流变原理相一致，本文定义的广义流变柔量、模量的表达式能描述蠕变柔量和松弛模量，从而验证了蠕变和松弛是广义流变的两种特殊形式，描述了流变的广义特征。

由试验结果可知，不同方向系数α条件下，三城目安山岩的σc和εr见图5。3个区域中，应力水平越大，关联应力和关联应变的绝对值都增大；区域Ⅱ中，方向系数α越大，关联应变值减小，关联应力值增大。

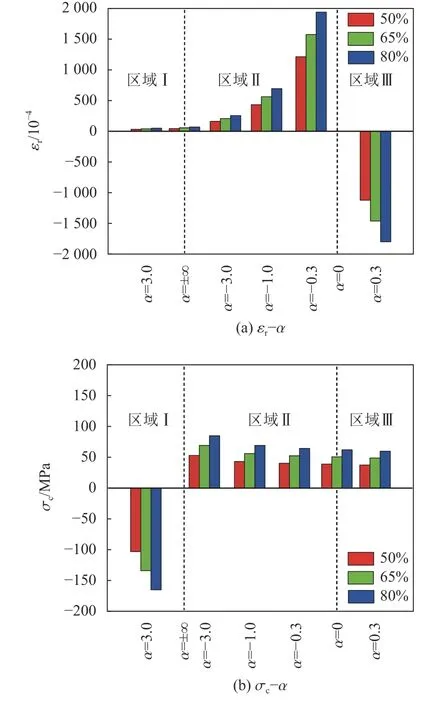
图5 三城目安山岩广义关联应变和应力Fig. 5 Generalized related strain and stress for Sanjome andesite

图6为80%应力水平下，田下凝灰岩广义流变柔量和三城目安山岩广义流变模量随时间的变化规律。图6（a）中：6个方向系数α下，田下凝灰岩广义流变柔量随时间增加而增大；当 α=−0.3时，广义流变柔量时间依存性最大；当 α=±∞时，广义流变柔量时间依存性最小。图6（b）中：6个方向系数α下，三城目安山岩广义流变模量随时间增加而增大；当 α=0.3时，广义流变模量时间依存性最大；当 α=3.0时，广义流变模量时间依存性最小。对6个方向系数下的广义流变柔量、模量的数据在同一时刻求平均值，如图6中虚线所示；对广义流变柔量、模量进行数值拟合，如图6中实线所示，平均值大于拟合曲线值。

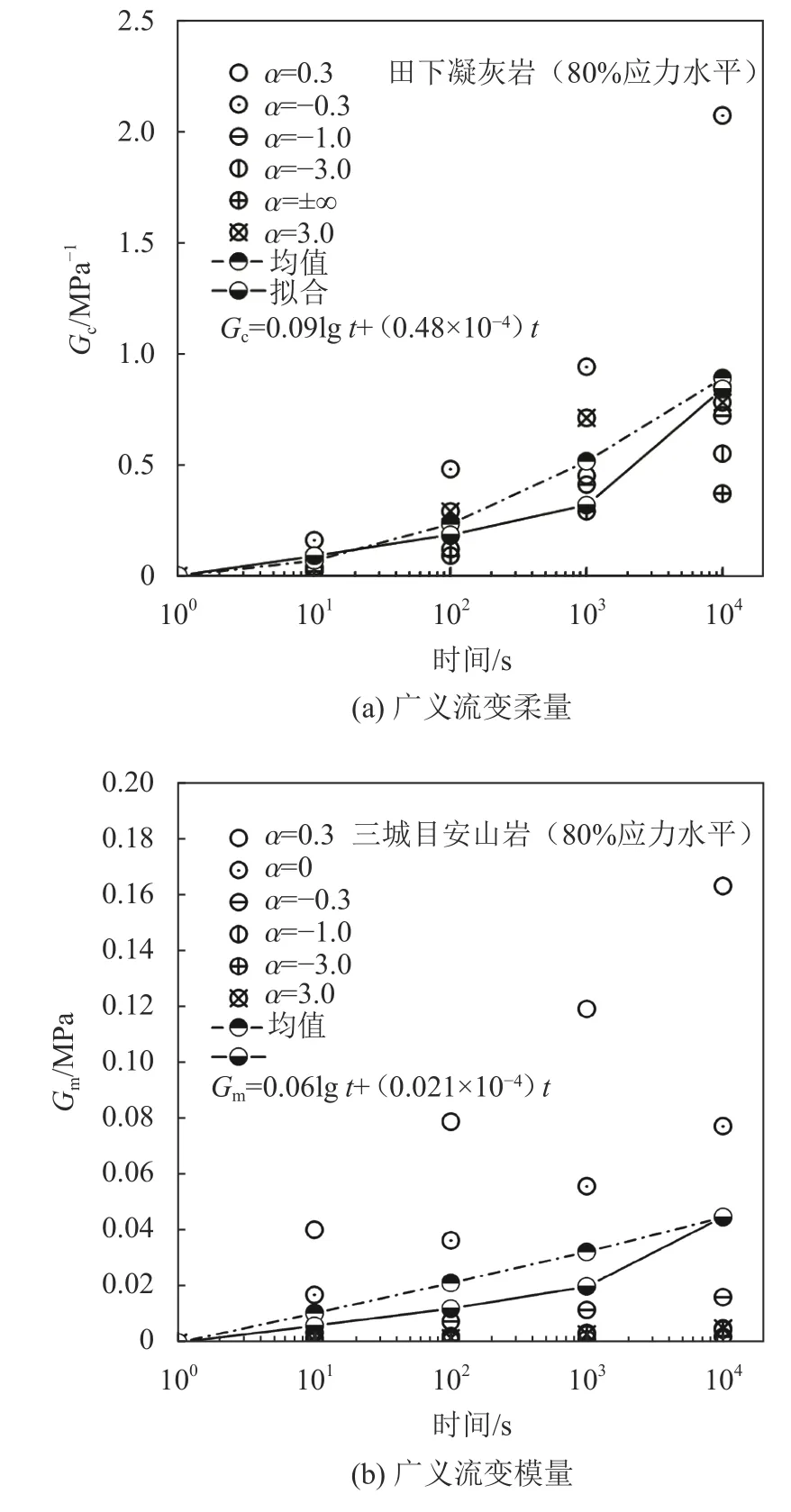
图6 广义流变柔量、模量的时间依存性（80%应力水平）Fig. 6 Time-dependency for generalized rheological-compliance and modulus at 80% stress level

由以上分析可知，广义流变柔量、模量拟合结果呈非线性流变特征，两种岩石的拟合公式如下：

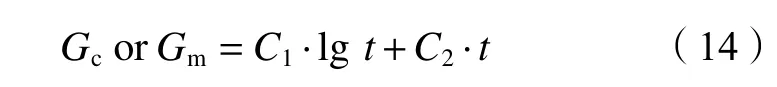
式中，Gc为广义流变柔量，Gm为广义流变模量，C1和C2为拟合参数，t为时间。两种岩石拟合参数如表2所示，随着应力水平增加，参数C1和C2都增大，可认为随着应力水平的增加，广义流变柔量和模量都增加，具有明显的时间依存性和应力水平依存性。

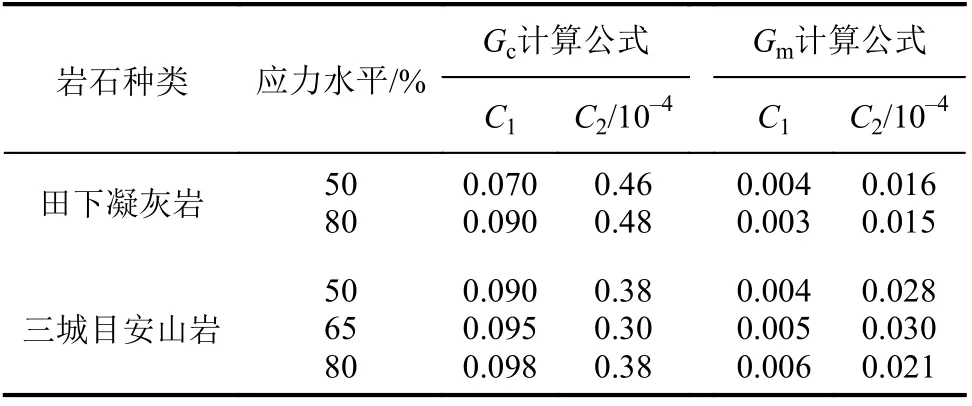
表2 两种岩石广义流变柔量和模量拟合系数Tab. 2 Fitting parameters of generalized rheologicalcompliance and modulus for two rocks

图7（a）为田下凝灰岩在不同方向系数α下的广义流变柔量变化规律，可知广义流变柔量具有明显的时间依存性，但方向系数依存性不明显。图7（b）为三城目安山岩在不同方向系数α下的广义流变模量的变化规律，和广义流变柔量一样，具有明显的时间依存性，但对方向系数依存性不敏感。

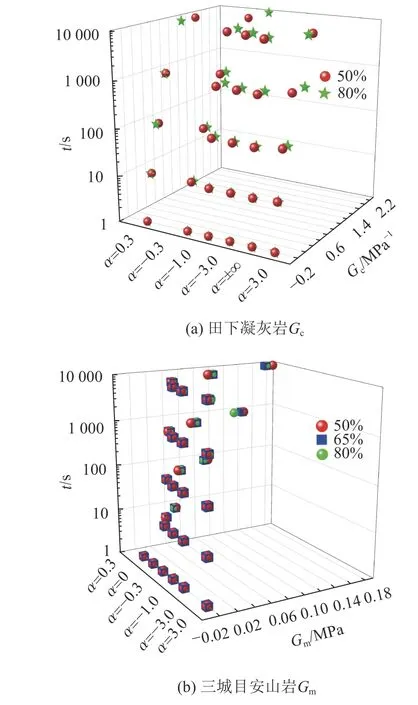
图7 广义流变柔量、模量的方向系数依存性Fig. 7 Direction coefficient-dependence for generalized rheological-compliance and modulus

3 讨 论

对线弹性材料而言，蠕变柔量和松弛模量互为反比例关系，呈线性流变特征，两者没有本质区别。蠕变柔量和松弛模量是广义流变的主要内容，是岩石流变力学理论的重要特性，应力归还控制的广义流变试验，为研究广义流变相关特性提供了试验基础。本文定义的广义流变柔量和模量计算方法具有广义性，当 σc=σcrp时 ，可计算蠕变柔量；当 εr=εrelax时，可计算松弛模量。田下凝灰岩和三城目安山岩具有非线性黏弹性特性，其广义流变柔量和模量之间的关系如图8所示。Gc/Gm比值可认为是岩石局部刚度，在峰前80%应力水平下，随着时间的增加，两种岩石的局部刚性都在减小，故可认为两种岩石破坏前塑性变形都增加，岩石刚性和塑性变形呈反比例关系。这一结果能解释岩石的破坏机理，并为以后在研究中将岩石刚性和塑性变形进行分离，并定量分析两者之间的关系奠定了基础，也为未来研究岩体刚性下降规律、支护后强度恢复和长期稳定性等方面提供了思路。但峰后Gc/Gm比值还未知，需要继续追加大量试验，可作为未来研究课题。

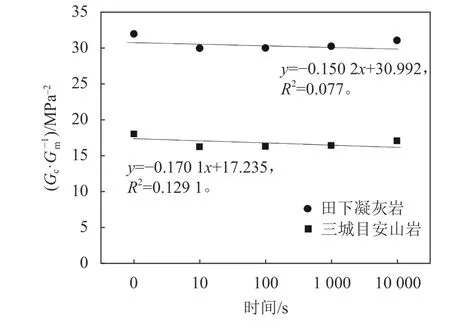
图8 广义流变柔量与模量的关系（80%应力水平）Fig. 8 Relationship between generalized rheological-compliance and modulus at 80% stress level

4 结 论

本文在广义流变理论基础上，以应力归还控制法执行了Ⅰ类和Ⅱ类岩石的广义流变试验，对广义流变柔量和模量进行了系统研究，主要结论为：

1）提出了一种计算广义流变柔量和模量的方法，该方法具有广义特性，可描述材料的非线性流变特性。

2）Ⅰ类和Ⅱ类岩石广义流变柔量和模量具有明显的时间依存性和非线性流变特征，其两种规律具有相似性。

3）对线性黏弹性材料而言，蠕变柔量和松弛模量之间可相互转换，没有本质的区别。但在岩石的非线性黏弹性行为中，广义流变柔量和模量具有非线性流变特征，且在破坏前两者比值逐渐减小，说明接近破坏前，岩石刚性逐渐降低，此现象可定量研究岩体的流变现象和破坏机理，对评估地下工程的长期稳定性具有重要的意义。