基于水土耦合的沟床起动型流体运动过程模拟研究

潘华利，李炳志,3，邓其娟，欧国强，孔 玲,3

(1.中国科学院 水利部 成都山地灾害与环境研究所，四川 成都 610041；2.中国科学院 山地灾害与地表过程重点实验室，四川 成都 610041；3.中国科学院大学，北京 100049；4.四川建筑职业技术学院，四川 成都 610399)

沟道流体运动的动力过程决定着流体容重的变化过程，在流域极端降雨条件下，流体沿沟道流动过程中容重的变化规律又直接决定着沟道各处流体的类型[1]，从而决定着各沟段是否有泥石流发生。如果能够根据流域所具备的物源条件判断其在流域极端降雨条件下各沟段是否会暴发泥石流，对于进行流域风险评估、防治工程设计以及潜在性泥石流沟判识等具有重要意义。目前，围绕泥石流动力过程研究领域，国内外学者开展了大量研究。例如，Cao[2]及Wu[3]等基于浅水流动守恒定律，建立了动床条件下1维溃坝洪水的水沙耦合模型，详细研究了水流演进过程中水沙与床面的相互作用；Simpson等[4]在Cao等[2]的基础上引入了泥沙浓度守恒式，独立处理泥沙的侵蚀及沉积，将水沙耦合模型扩展到2维；何思明等[5]基于极限分析的上限定理，研究了黏性泥石流运动对沟道土体的侵蚀启动机制，得到了泥石流侵蚀启动速度的表达式；廖丽萍等[6]从土力学角度进行土体临界状态分析，探讨了土体性质对泥石流起动的影响；为探索降雨型泥石流对沟床的侵蚀机理，吴永[7–8]等借助水力学理论，在科学表征泥石流流深的前提下，分析了沟床在泥石流流动剪切和渗流水压耦合作用下的侵蚀机理；为了对坡面–沟道间土壤侵蚀的时空关系进行合理耦合，高佩玲等[9]对小流域侵蚀动态过程进行分析，建立了流域系统土壤侵蚀动态过程模拟模型；王钧[10–11]等采用分布式水文模型得到流域径流过程，根据径流条件计算得到沟道各处固体物源厚度，反演计算了各子流域出口处流体自由表面的变化过程；乔成[12]将流体固液两相分开考虑，构建了考虑颗粒剪胀效应和动床侵蚀作用的深度积分泥石流两相动力学模型。

上述研究表明，在建立流体运动模型时，大多学者考虑了沟床侵蚀对流体运动状态的影响，而将沟床侵蚀及坡面汇流综合考虑，并将其与来流流体合理耦合的研究成果相对较少。本研究从泥石流暴发所必须的物源条件及水动力条件出发，在充分分析沟床可移动固体物源侵蚀过程的基础上，将具有时空变异性的坡面汇流及上空降雨合理地分配于沟道中，将来流流体、被侵蚀的固体物源、坡面汇流以及上空降雨4部分进行合理耦合，建立了沟道流体运动的水土耦合模型；采用迎风差分格式及欧拉公式对模型进行数值离散，得到流体运动数值离散模型；基于MATLAB语言对流体运动数值离散模型进行编程求解，可得到各沟段流体容重的动态变化过程，从而为流域开展防灾减灾工作及进行潜在性泥石流沟判识等奠定理论基础。

1 沟道流体运动水土耦合模型的建立

1.1 流体运动的水土耦合方程

流体沿沟道流动的过程中，除受到沿程坡面汇流及上空降雨两部分水体补充外，还会侵蚀沟道内的可移动固体物源得到物源补充。物源被侵蚀后，会与上游来流、两侧汇流及上空降雨混合，共同流向下游，致使流体运动参数不断发生变化，流体流动示意图如图1所示。

图1 流体沿沟道流动示意图Fig. 1 Schematic diagram of fluid flow along the channel

假设汇水坡面为基岩，则坡面汇流只对沟道补充水体，不补充泥沙。同时，假设可移动固体物源沿沟道方向宽度不变且物理力学性质均一，则流体中的固相颗粒和液相浆体沿x方向的体积守恒方程可表示为：

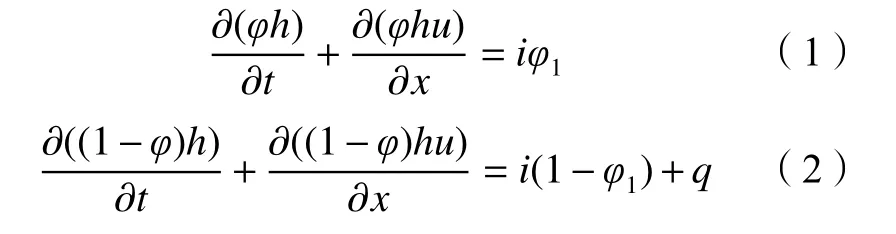
式中：方程右边项是指物源、汇流及上空降雨进入流体所引起的固液两相组分体积的增加；x为笛卡尔坐标，m；t为 时间，s；h(x,t)为 流体深度，m；u(x,t)为流体流速，m/s；φ(x,t) 为流体中粗颗粒的体积浓度；i为单位宽度固体物源被侵蚀的速率，m/s；φ1为固体物源中粗颗粒的体积浓度；q(x,t)为坡面汇流及上空降雨对单宽沟道的水体补充量，m/s，其包括坡面侧流及上空降雨两部分，可表示为：

式中：p为降雨强度，m/s；w为沟道宽度，m；qs为坡面侧流对单位长度沟道的水体补充量，m3/s。

固相颗粒和液相浆体动量守恒方程可表示为：

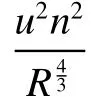
方程（4）和（5）右边第1项是重力沿斜坡向下的分力，第2项是由于流体自由表面变化所引起的控制体前后两侧的压力差，第3项是底床摩擦阻力，第4项是物源进入流体所引起的动量变化。

1.2 流域汇水坡面划分及坡面汇流量计算

流域汇水坡面的水流沿汇水方向从不同点进入沟道，使得汇水坡面对沟道的水体补充随时间和空间而发生改变。如图2所示，为了处理具有时空变异性的汇流，本研究根据汇流区的坡度和下垫面情况沿沟道方向将汇水坡面划分为多个汇水分区。采用由美国农业部发明的用于计算小流域坡面汇流过程的SCS汇流模型分别计算每个汇水区的江流情况[14–17]。再依据各汇水分区与沟道的连接关系将坡面汇流量分配于沟道中，实现坡面−沟道间的合理耦合。

图2 小流域汇流区划分示意图Fig. 2 Schematic diagram of the division of small watershed confluence area

采用SCS汇流模型对汇水区进行汇流计算时，首先将一整场降雨划分为多个净雨时段，根据SCS汇流模型，在一次净雨时段中，峰现时间和洪峰流量分别为：

式（6）～（7）中：tp为 峰现时间，h；qp为洪峰流量，m3/s；Q为一次降雨的净雨量，mm；A为 汇水区面积，km2；l为汇流长度，m；y为坡度的百分数；S为流域场次降雨最大滞留量，m；净雨量Q及场次降雨最大滞留量S可表示为：式（8）～（9）中：I为时段降雨量，mm；CN为反映降雨前流域特征的一个综合参数，它与流域前期土壤湿润程度、坡度、植被等因素有关。

1.3 沟道可移动固体物源侵蚀速率计算

可移动固体物源被流体侵蚀带走的过程可看作物源在水动力作用下起动运移的过程[18]。物源的稳定状态与外界降雨情况和地质构造作用紧密相关，在地下渗流和地表径流共同作用下，当其所受重力、剪切力等动力大于阻力时，固体物源间会存在一潜在滑动面，形成不稳定层[19–21]。此时，物源的重力势能有向动能和摩擦能转化的趋势[22]。根据杨顺[23–24]等建立的考虑饱和渗流及表面径流共同作用下可移动固体物源的临界力学判别模型，可将不稳定层厚度z表示为：

式中：γm为 流体容重，N/m3；β 为物源内摩擦角，(°)；θ为沟道坡角；d50为 物源中值粒径，m；γs为物源颗粒容重，N/m3；γw为 清水容重，N/m3；n1为 物源孔隙度；C为黏聚力，kPa；γsat为物源饱和容重，N/m3；

由于流体尚未到达的部分存在不动层的影响，认为不稳定层z不能瞬时地全体移动，侵蚀达到z深度需要一定的滞后时间[25]。滞后时间与流体流速、流体容重及堆积体物质组成紧密相关，将滞后时间表示为(αd50) /(uρT) ，则侵蚀速率i为：

式中，α为系数。

在流体侵蚀作用下，物源厚度不断减小，沟床地形变化可表示为：

式中，b为沟床地形，m。假设沟道某点物源初始厚度为d，则经过n∆t时刻物源剩余厚度dL为：

式中：∆t为侵蚀时间步长，s；ii为计算点对应时刻物源被侵蚀的速率，m/s。

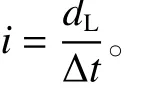
2 沟道流体运动模型的数值离散

为了对所建的流体运动模型进行连续求解，得到沟道各点处各时刻流体运动参数，需对其进行数值离散。数值离散方法采用有限差分法。其中，空间离散采用一阶迎风差分格式，时间离散采用欧拉公式。时空离散后，得到沟道流体运动数值离散模型如下：

式（14）～（17）中，上标n、n+1指时刻，下标j–1、j指控制点。

3 模型初始及边界条件处理

3.1 初始条件

初始时，流域无降雨，沟道内没有流体流过，初始条件为：

由于h要满足计算公式

故在初始时刻以一无穷小值 ε代 替h。

3.2 边界条件

1）汇水坡面与沟道的交汇处为模型内边界，沟道在交界处会受到坡面汇流的水体补充，汇流补充量为qs(x,t)，可根据所划分的各汇水分区采用SCS汇流模型计算得到。

2）沟道起点处流体的运动参数可根据沟口汇流区计算得到，起点边界条件可表示为：

得到模型初始条件及边界条件后，将其代入沟道流体运动数值离散模型，采用基于MATLAB语言编写的流体运动模型求解程序对其进行求解，便可得到沟道各点处各时刻流体的流深、流速、颗粒浓度及容重值。

4 模型验证

通过室内水槽实验对流体运动水土耦合模型进行验证，水槽实验在中国科学院、水利部成都山地灾害与环境研究所的山地灾害与地表过程重点实验室中进行。

4.1 实验模型

如图3所示，实验装置主要由供水装置、沟道模拟装置及降雨模拟装置组成。供水玻璃水槽尺寸为200 cm×20 cm×25 cm，用于给模拟沟道供水；沟道模拟水槽尺寸为200 cm×20 cm×45 cm，用于堆放实验物料，模拟泥石流沟道；沟道模拟水槽起点至100 cm处设置了不透水混凝土棱柱模型，以防止沟槽起点处物源被淘蚀而形成跌坎，避免过流流体紊动剧烈；降雨模拟装置位于沟道模拟装置正上方，其降雨喷头分布长度为120 cm，用于给沟道模拟水槽提供水体补充，模拟野外降雨及坡面汇流对实际沟道的水体补充。

图3 实验装置图Fig. 3 Experimental equipment

如图4所示，实验物料堆放长度为200 cm，堆放时使得物料上表面与供水水槽底面处于同一平面。为了消除物料与实验水槽底部明显的分界面的影响，在实验水槽出口处设置了高5 cm的侵蚀基准。

图4 实验物料照片Fig. 4 Experimental material photos

实验选取来流流量及沟槽坡度为控制变量，对所建的流体运动水土耦合模型进行验证。来流流量大小通过动力泵控制，动力泵可控流量范围为0～3 000 cm3/s，流量大小随动力泵开关的开合程度而发生变化，本实验根据动力泵开关可动范围设计6个档位，测量得到各档位对应流量分别为598、967、1 401、1 745、2 113、2 594 cm3/s。沟道模拟水槽坡度可调范围为0～15°，为在满足泥石流暴发所需的坡度条件下探索坡度对流体运动状态的影响，在坡度可控范围内均匀地设计5组变化值，分别为5°、7°、9°、11°、13°。同时，降雨模拟装置提供的水体补充量为310 cm3/s。侵蚀参数α和沟床表面糙度n为未知值，需要对其进行反复调校，找到最合适的参数值。采用12组水槽实验数据对模型参数进行调校，发现当侵蚀参数α为1.5×107，沟床表面糙度n为0.012 5时，流体运动模型的计算值与实验值有着比较高的吻合度。相关实验参数明细见表1。

表1 实验参数明细表Tab. 1 Experimental parameters

4.2 实验土体

实验过程中，所使用的物料取自于四川省都江堰市龙池镇干家沟，所用物料最大粒径为dmax=20 mm，实验水槽宽度与最大粒径比值为10，符合宽径比的要求[26]。实验前，抽取3组样品采用筛分法进行颗粒级配分析试验，得到物料级配图，如图5所示。

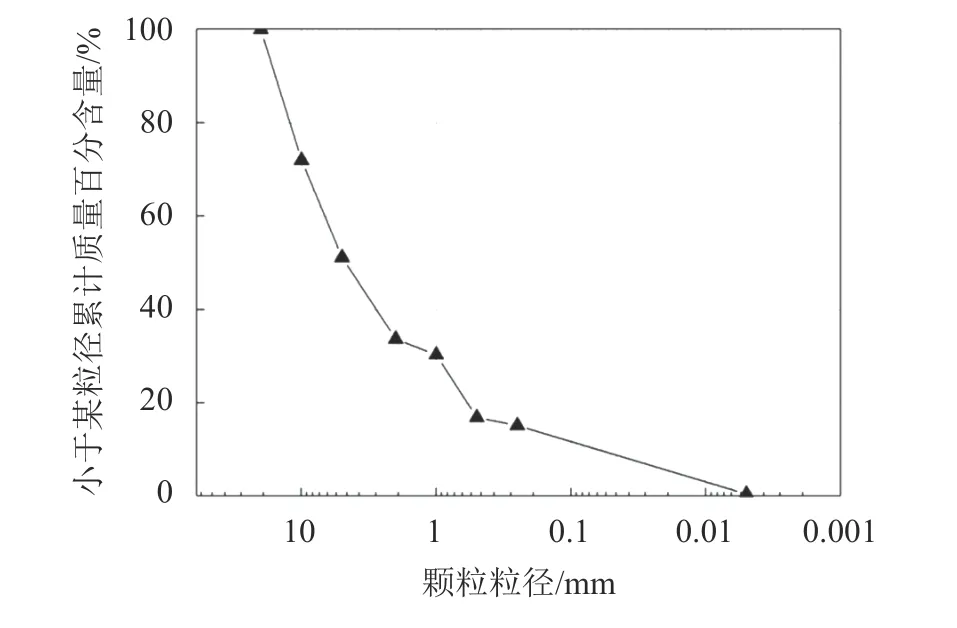
图5 干沟泥石流原样颗粒级配曲线Fig. 5 Particle grading curve of debris flow sample in Gangou

实验物料基础物理力学性质参数如表2所示。

表2 实验物料基础物理力学性质参数Tab. 2 Physical and mechanical property parameters of experimental materials

其中，实验物料颗粒密度采用2 000 mL量筒通过水中置换法进行3次测量求取平均值得到；饱和密度通过环刀取3组样品，然后向样品中滴水至饱和状态，测量后求取密度平均值得到；内摩擦角及黏聚力的测量如图6所示，通过由直剪试验在4种不同垂直压力下的应力应变曲线所绘制的莫尔圆得到。

图6 直剪试验测量内摩擦角及黏聚力Fig. 6 Measurement of internal friction angel and cohesion by direct shear test

4.3 实验量测参数

选取沟道模拟水槽控制点，测量不同工况条件下各控制点处流体流深、流速和流体容重，将其与理论模型计算值进行对比，以验证所建理论模型的合理性。如图7所示，本实验共选取2个控制点，为避免降雨模拟装置对流深及流速的测量造成影响，控制点应选在降雨模拟装置分布以外的区域，故将1号控制点设置于沟道模拟水槽下游140 cm处，2号控制点设置于沟道模拟水槽出口处。

图7 控制点分布图Fig. 7 Distribution map of control points

实验过程中，采用摄影法结合激光测距法对流体流深进行测量。在实验水槽侧面安装索尼HDR–PJ670高速摄影机记录流体运动过程，通过影像解译获取控制点处各时刻流体流深。同时，于控制点上方安装测量精度为1.5 mm的RLM–S30C激光测距仪，测量流体自由表面高程的变化过程，并与通过摄影得到的流体液面高程变化过程进行对比，以保证通过影像解译得到的流体流深的准确性。流速的测量采用浮标法，于供水水槽上游投掷乒乓球浮标，通过水槽侧面的高速摄影机记录浮标流至控制点处的运动过程，通过影像解译计算得到控制点处各时刻流体的流速。流体容重通过在出口处取样得到，当流体流出沟道出口时，不断用量筒于出口处取样，同时通过水槽前方的摄影机记录各样本的取样时刻，待实验完成后测量样本的质量及体积，计算得到沟道出口处各时刻流体的容重，并取平均值即得到当前工况条件下沟槽出口处流体的容重值。流体运动参数测量的实验过程照片如图8所示。

图8 实验过程照片Fig. 8 Experimental process photos

4.4 实验与理论结果对比

1）流体流深实验结果与理论结果对比分析

图9、10分别为不同来流流量条件下两个控制点处流体流深实验值与计算值的变化及对比。图9和10表明：不同来流流量条件下，沟槽两个控制点处流深实验值与计算值变化趋势相同，均随来流流量的增加而不断增大；但流深的实验值略大于计算值。其原因是：流体从供水水槽流入物源区时，会先对接覆土较薄的物源区进行冲刷，致使混凝土棱柱模型与物源堆积体的衔接面下移，流体流经衔接面时，过流表面的变化会增加流体的紊动作用；同时，物源堆积体表面的凹凸不平也会促使过流流体紊动作用增强，致使通过高速摄影机观测到的流体流深略大于其计算流深。对流深进行误差分析，发现控制点1和出口处流深实验值与计算值的相对误差分别为14.3%和16.7%。

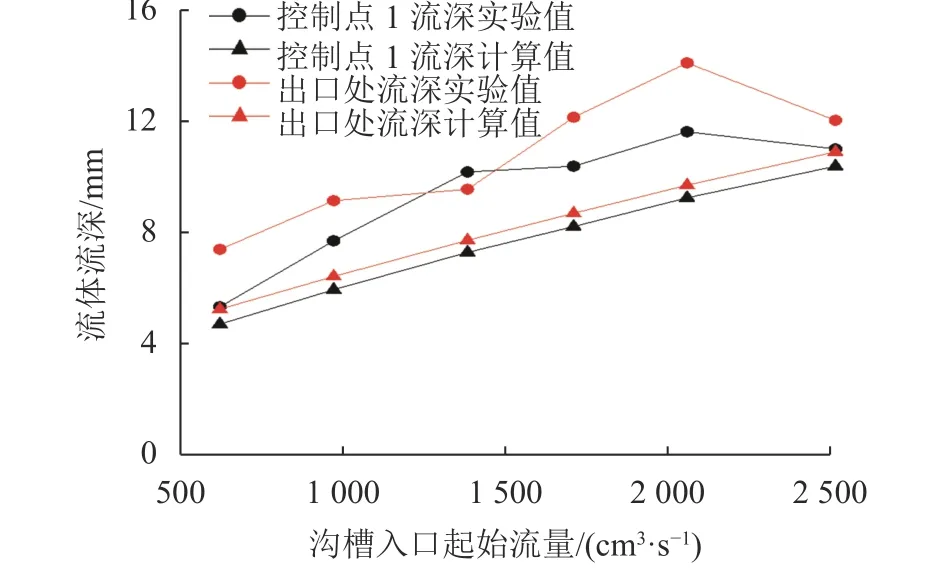
图9 流体流深变化Fig. 9 Evolution of fluid depth

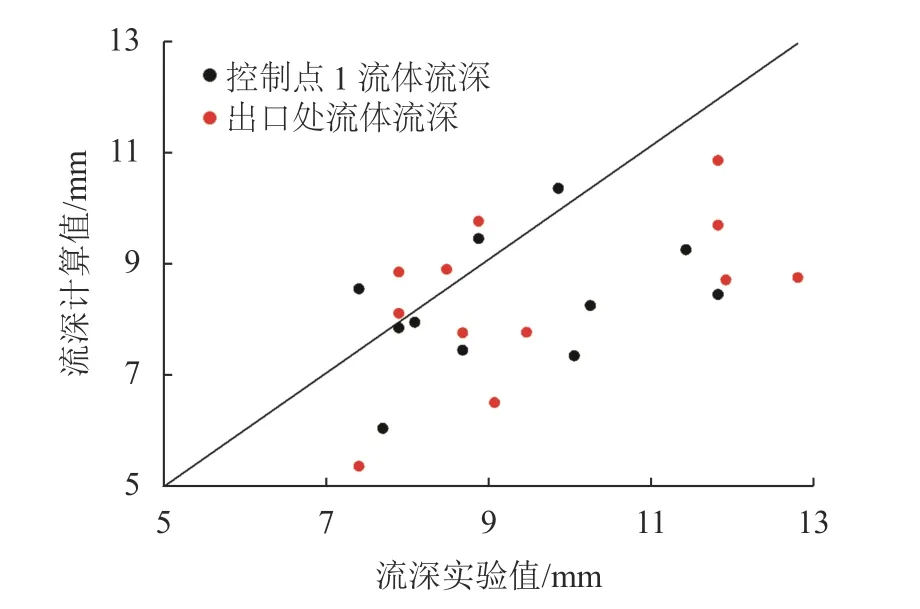
图10 流深实验值与计算值对比分析Fig. 10 Comparative analysis chart of the experimental value and calculated value of fluid depth

2）流体流速实验结果与理论结果对比分析

不同流量条件下流速实验结果与理论结果对比情况见图11、12。由图11和12可见，两个控制点处流速的实验值与计算值吻合良好，且均随来流流量的增加而不断增大。其原因是：来流流量越大，单位时间通过沟道横截面的流体越多，所对应的沟道各点处的流速便越大。误差分析发现控制点1和出口处流速实验值与计算值的相对误差分别为5.7%和6.1%。

图11 流体流速变化Fig. 11 Evolution of fluid velocity

图12 流速实验值与计算值对比分析Fig. 12 Comparative analysis chart of the experimental value and calculated value of fluid velocity

3）流体容重实验结果与理论结果对比分析

不同流量条件下容重实验结果与理论结果对比情况如图13、14所示。由图13和14可见，流体容重实验结果与理论结果吻合度较高，且均随来流流量的增加而呈逐渐减小的趋势，这是来流流量的增加对流体产生的稀释作用所致。对其进行误差分析，发现出口处容重实验值与计算值的相对误差为5.3%。

图13 出口处流体容重变化Fig. 13 Evolution of fluid bulk density at the outlet

图14 出口处容重实验值与计算值对比分析Fig. 14 Comparative analysis chart of experimental value and calculated value of bulk density at the outlet

综上所述，沟道各点处流体流深、流速和容重实验结果与理论结果的相对误差均小于20%。其中，流体流速和容重的模拟精度均高于90%，流体流深的模拟精度高于80%，表明沟道流体运动的水土耦合模型侵蚀参数的确定较为合理，采用该模型对沟道流体运动过程进行模拟基本可行。

5 结 论

本研究包含以下研究成果：

1）沿着沟道方向，根据汇水坡面坡度及下垫面情况划分汇水区，根据坡面与沟道间的连接关系将坡面汇流量分配于沟道之中，实现了坡面−沟道间时空关系的合理耦合，在此基础上建立了考虑沟床侵蚀和坡面汇流的沟道流体运动的水土耦合模型。采用欧拉公式和迎风差分格式对流体运动水土耦合模型进行时空离散，得到了沟道流体运动数值离散模型。

2）通过分析水槽实验数据，发现沟道各点处流体流深、流速与来流流量呈正相关关系，流体容重与来流流量呈负相关关系。

3）对比分析模型实验结果与理论计算结果，发现流体流深、流速和容重的实验值与模拟值的相对误差均小于20%。流体流速和流体容重的模拟精度高于90%，流体流深的模拟精度高于80%，表明该小流域沟道流体运动水土耦合模型及其数值计算方法基本合理，采用该模型模拟动床作用下沟道流体运动过程基本可行。