低速冲击下C型冷弯薄壁钢构件动力响应分析

吴 长，王仁红，丁金伟

(1.兰州理工大学 土木工程学院，甘肃 兰州 730050；2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，甘肃 兰州 730050)

冷弯薄壁钢构件具有轻质高强、绿色环保的优点，广泛应用于工业厂房、低层建筑等的主要承重构件[1]。然而，建筑物在使用的过程中可能突然遭受碰撞、自然灾害及爆炸等偶然荷载，当建筑物受力构件受到这些偶然荷载的作用时，构件将产生变形甚至失效，对结构的安全性有着严重的威胁。因此，研究冷弯薄壁钢构件在冲击荷载作用下的变形模式和动力响应十分重要。

根据研究和统计数据表明，意外碰撞是结构破坏的主要原因之一，国内外学者对于冲击荷载作用下构件的研究主要集中在钢筋混凝土构件、铝合金梁构件等[2–4]。对于冲击荷载作用下冷弯薄壁型钢梁方面的研究，Liu等[5]认为梁的失效模式分为拉伸撕裂破坏和剪切破坏，并且冲击点靠近支座时梁的吸能能力急剧下降。Yu等[6–7]提出梁动力响应过程中的临界条件和相应的失效准则。Kenny等[8]通过总结影响动态屈曲的参数，对钢梁的动态塑性屈曲进行研究。杨娜等[9]对C型构件的滞回性能以及压弯屈曲机理进行了研究。张辉[10]研究了C型冷弯薄壁钢梁的受剪性能。苗二萍等[11]分析了冷弯薄壁钢梁的变形性能，并提出了适用于变形计算公式的折减系数。霍静思等[12]研究了冲击速度和能量对热轧H型钢梁力学性能的影响。王蕊等[13]认为冲击能、冲击物质量和冲击速度对钢梁的动力响应有不同程度的影响。裴畅[14]研究了H型钢构件冲击荷载作用下构件的力学性能以及冲击后构件的剩余承载力。崔娟玲等[15]用两种不同边界的热轧H型钢柱通过落锤式冲击试验得到试件的破坏形态和残余应变。王春刚等[16]对腹板开孔的复杂卷边槽钢进行轴压试验，得出腹板开孔导致构件的承载效率下降，孔洞附近出现较大应力区域和最大应力点。时聂涛[17]对梁冲击响应的多种因素进行分析，并得到了钢梁在不同冲击作用下发生屈曲的临界冲击荷载。张旭等[18]研究得到不同冲击能量作用下翼缘对卷边的约束作用明显不同，提升冲击速度，构件动态屈曲临界荷载相应增大。国内外众多学者对于对H型钢梁在不同方向的冲击荷载下的动力响应、动态屈曲等方向做出了广泛的研究，但缺乏开口薄壁构件在偶然荷载作用下的相关研究，因此，本文进行了冲击荷载作用下冷弯薄壁槽钢梁的试验研究以及数值模拟的动力响应分析，为评估冷弯薄壁型钢构件在横向冲击作用下的安全性提供了参考依据。

1 实验装置及简介

1.1 实验目的

对两组共12个冷弯薄壁钢构件进行冲击物不同速度下的冲击试验，提取测点处的应变、位移等动力响应数据，分析冲击物不同质量、不同速度对C型薄壁钢构件变形模式的影响。通过试验结果和有限元数值模拟结果对比分析，验证有限元数值模拟结果的有效性。

1.2 试件设计及试验工况

试件尺寸参考有限条软件（elastic buckling analysis software module，CUFSM）计算中以畸变屈曲为主的构件尺寸确定，试件的几何尺寸与截面形状如图1、表1所示。试验冲击工况如表2所示。

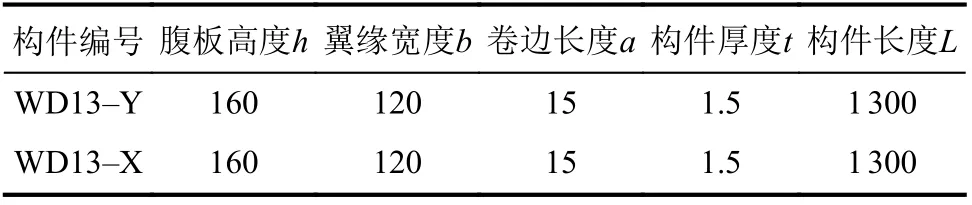
表1 构件尺寸Tab. 1 Member sizes mm

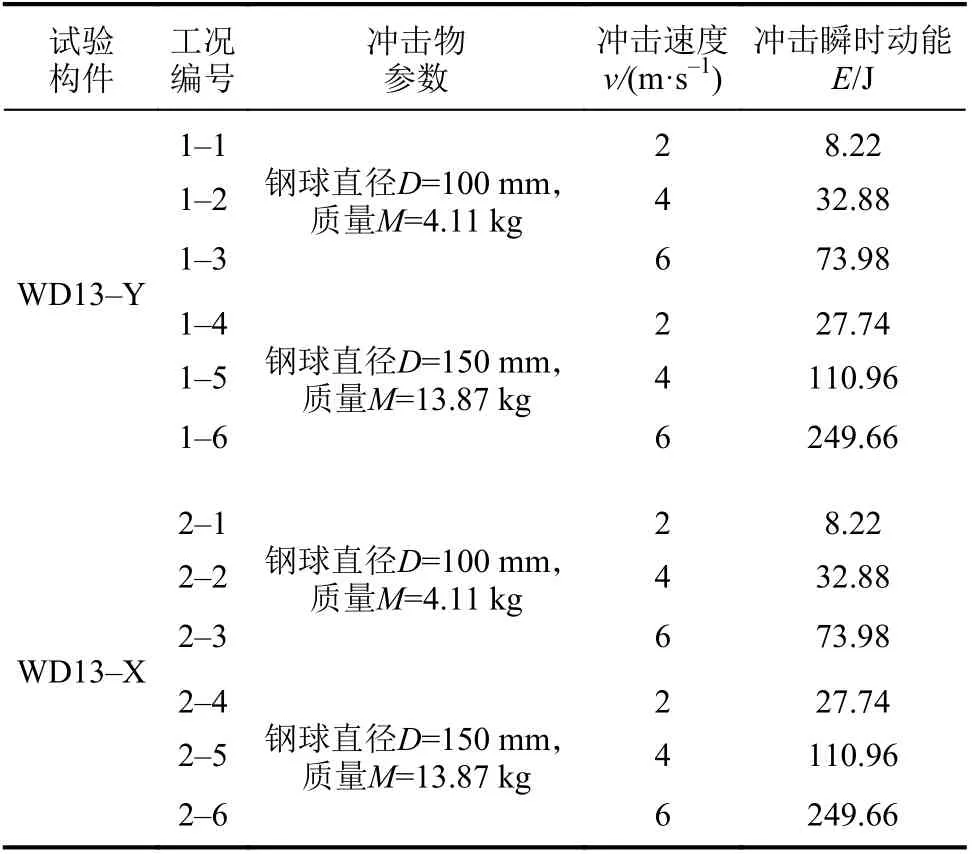
表2 冲击试验工况Tab. 2 Impact test conditions

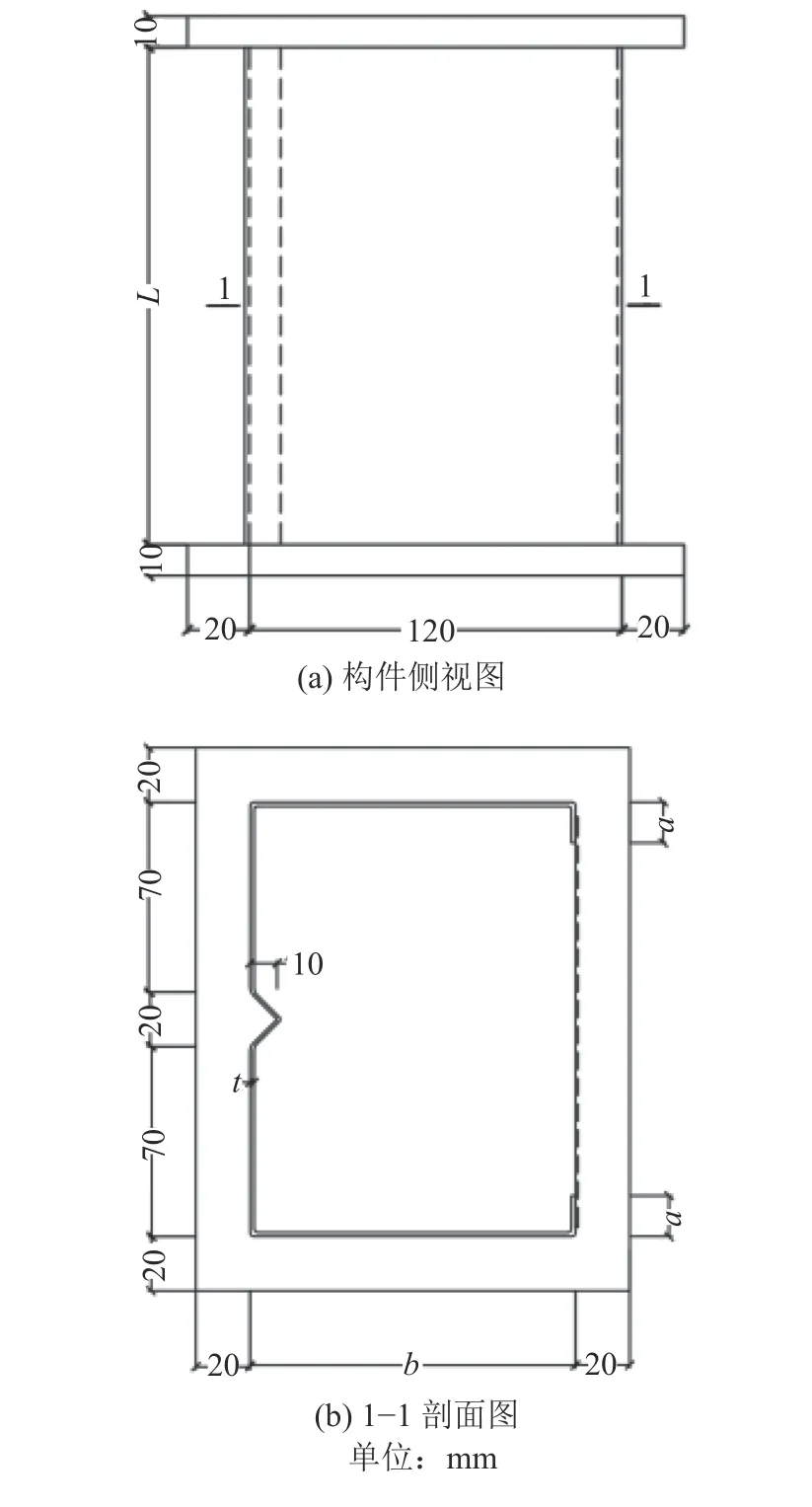
图1 构件截面尺寸Fig. 1 Members cross-sectional dimensions

1.3 构件材料属性

依据《金属材料拉伸试验 第1部分：室温试验方法》（GB/T228.1—2010）的规定[19]，对6个拉伸试验标准板状试样进行拉伸试验，分析试样的应力–应变曲线，得到试样的基本材料参数，如表3所示。

表3 钢材材料参数Tab. 3 Steel material parameters

1.4 试验装置

冲击试验系统由10 t单梁桥式起重机、电磁铁以及通过高强螺栓与地面连接的H型钢支座组成，如图2所示。支座与立柱、立柱与试件采用高强螺栓进行连接。冲击试验中，利用起重机将吸附钢球的电磁铁提升到预定的高度，通过控制箱退磁，钢球以自由下落的方式对构件施加荷载。

图2 冲击试验系统及试验装置Fig. 2 Impact test system and test device

2 有限元模型

采用有限元分析软件ANSYS/LS–DYNA，建立C型冷弯薄壁钢构件的有限元模型，C型冷弯薄壁钢梁采用SHELL163薄壳单元，工字钢立柱、螺栓及冲击物采用SOLID164实体单元，冲击物分别为直径100和150 mm的球形刚体。冲击物与构件的接触算法采用基于罚函数的面–面自由接触算法。

文献[20]研究结果表明，应变率对结构承受短时超强荷载有较大影响。LS–DYNA中的分段线性塑性模型能够较好地模拟钢材承受突加强动荷载的作用。钢材的分段线性塑性模型的应力–应变曲线如图3所示。冲击物采用刚性材料模型，材料模型的参数如表4所示。

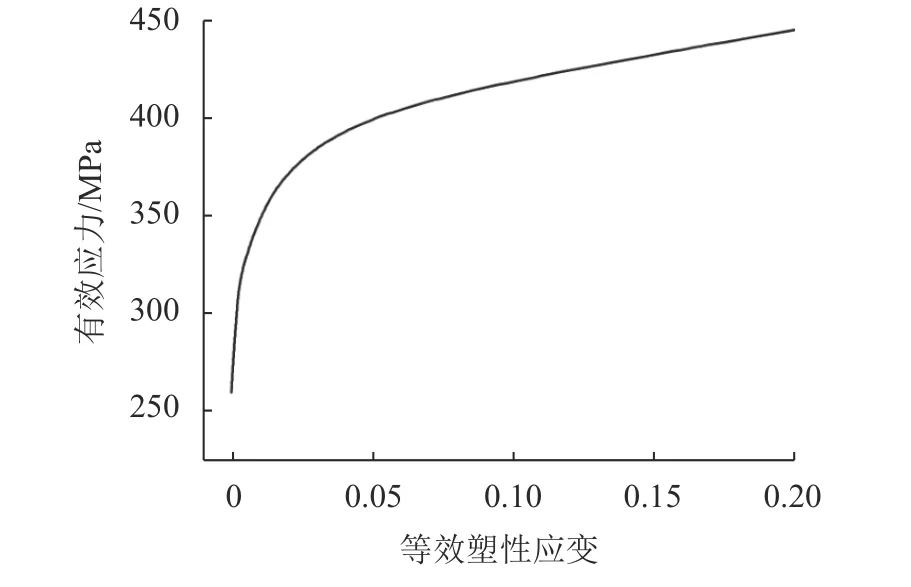
图3 钢材分段线性塑性模型Fig. 3 Piecewise linear plasticity model of steel

表4 各材料参数Tab. 4 Material parameters

C型冷弯薄壁钢构件网格划分采用映射方式，翼缘、腹板网格为20 mm×10 mm，由于H型钢支座、螺栓和封口板用于固定构件，采用自由划分的方式划分网格。为确保有限元模型得到的数据更加精确，构件采用与试验相同的螺栓与立柱相连接的半刚性约束。

3 试验结果与有限元结果对比分析

3.1 变形模式对比

冲击试验结束后，构件冲击区局部变形形态及破坏模式如图4所示。

图4 试件局部变形Fig. 4 Specimen local deformation

由图4可知：随着冲击速度增大，构件的变形情况分别为：冲击区无明显变形、冲击区轻微凹陷、冲击区局部凹陷；增大冲击物质量，冲击物惯性增大，导致构件冲击区凹陷变形程度明显增大，其中，构件翼缘向外凸起导致构件失效破坏如图4（d）所示。

WD13–Y和WD13–X构件的最终变形模式如图5所示。

由图5分析可知：当冲击力作用方向垂直于C型冷弯薄壁钢梁截面的弱轴时，构件冲击区腹板大面积向内凹陷，上、下翼缘各自绕着腹板和其交线向外转动；而当冲击力作用方向垂直于C型冷弯薄壁钢梁截面的强轴时，构件腹板向外轻微鼓起，上、下翼缘各自绕着腹板和其交线向内转动。构件的试验结果和有限元数值模拟结果的变形模式相近，验证了有限元模式结果的有效性。

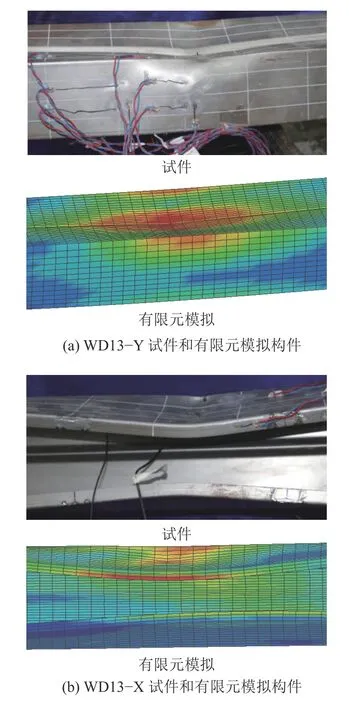
图5 构件最终变形模式Fig. 5 Member final deformation modes

3.2 位移极值分析

冲击过程中，构件的位移瞬间达到极值然后恢复到一个稳定值，位移极值是反映构件动力响应的重要指标。构件的X轴为强轴，Y轴为弱轴，冲击力垂直于构件Y轴时，构件的抗冲击性能弱于冲击力垂直于X轴；相同冲击条件下，构件WD13–Y的位移极值大于构件WD13–X。冲击物速度与构件位移极值的增量近似成比例关系，如图6、7所示。

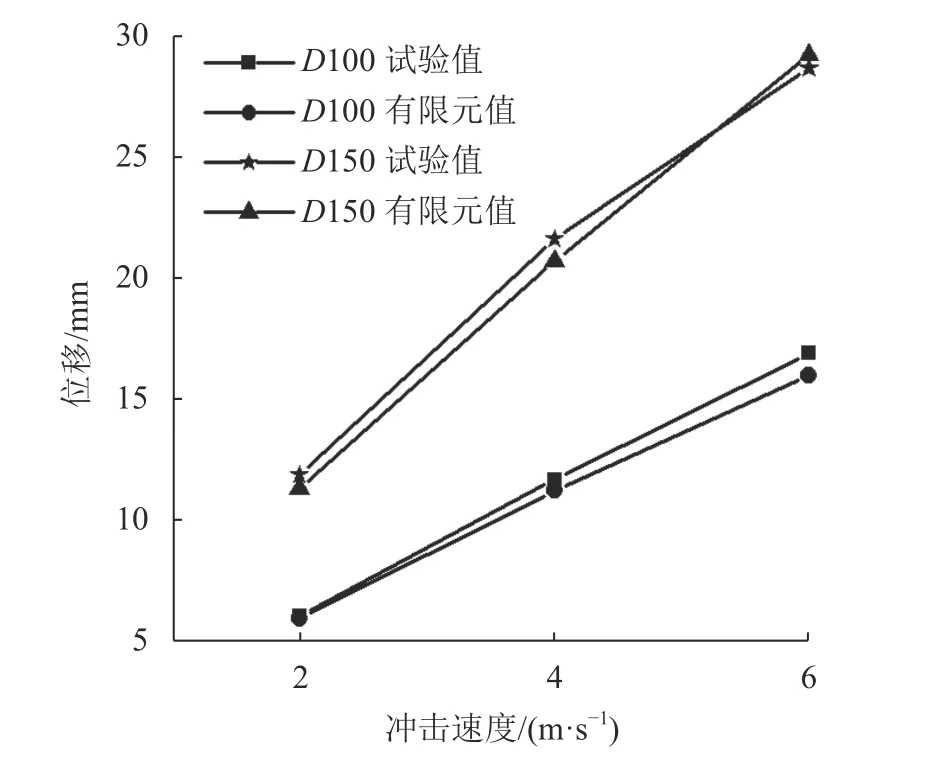
图6 WD13–Y构件位移极值Fig. 6 WD13–Y extreme value of member displacement

分析图6、7可得：WD13–Y试件试验位移极值与有限元位移极值最大差值为0.93 mm，最大差值与试验位移极值的比值为4.30%，与有限元位移极值比值为4.49%；WD13–X试件试验与有限元的位移极值最大差值为1.23 mm，最大差值与试验位移极值的比值为6.72%，与有限元位移极值的比值为7.20%。试件位移极值的试验值和有限元的差值极小，试验结果与有限元结果相吻合。

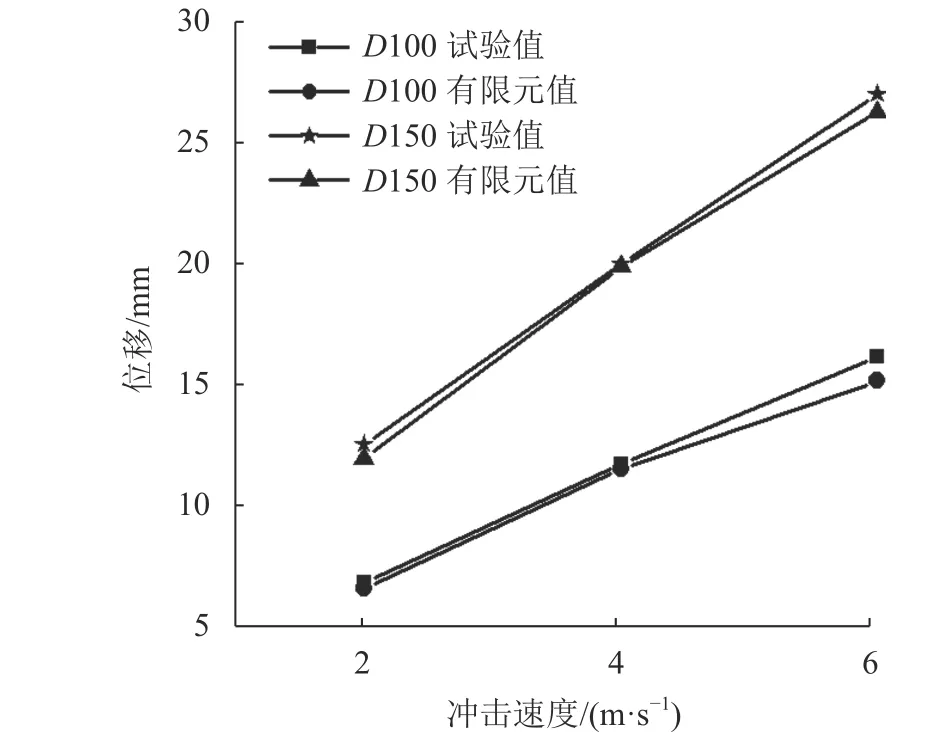
图7 WD13–X构件位移极值Fig. 7 WD13–X extreme value of member displacement

4 变形模式分析

位移是构件发生变形最直观的反映，通过分析冲击物密度、速度和冲击角度的位移云图，可直观观察构件达到最大变形时各部分的变形情况，从而得到不同冲击参数对钢梁构件动力响应的影响规律。

4.1 冲击物密度对变形模式的影响

不同密度的冲击物作用下构件位移云图如图8所示。

分析图8可得：冲击过程中，当冲击能量施加给构件后，冲击波从冲击区向四周传播，构件上、下翼缘均向内凹陷。冲击物密度为2000、4 000、6 000和8 000 kg/m3时冲击区最大位移值分别为13.13、18.15、20.75和23.11 mm；随着冲击物密度增大，构件冲击区最大位移值逐渐增大，非冲击区也出现变形，且最大位移出现在构件上翼缘外边缘处和冲击点处；冲击物密度的增大，冲击能量增大，构件最大位移集中在上翼缘外边缘处和冲击点处，出现较大凹陷变形，增加冲击物密度，构件从冲击点处和上翼缘外边缘处因丧失承载能力而失效。

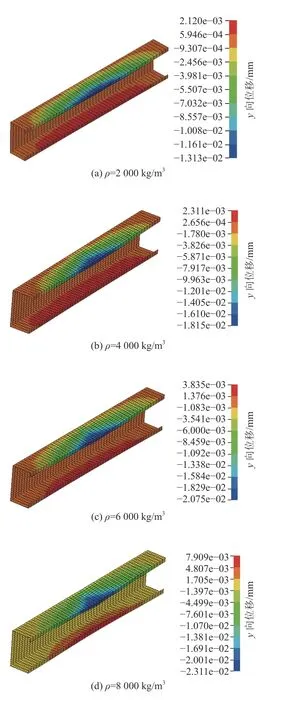
图8 不同冲击物密度下的位移云图Fig. 8 Displacement cloud graph under different impactor densities

4.2 冲击物的冲击速度对变形模式的影响

不同冲击物速度下构件的位移云图如图9所示。

分析图9可得：随着冲击速度的增大，构件凹陷变形程度增大；速度为3 m/s时，构件冲击区竖向位移值均小于10.00 mm，冲击区轻微凹陷，构件下翼缘竖向位移小于1.20 mm，向内凹陷但不明显；速度为6 m/s时，构件冲击区竖向位移在10.00至16.62 mm之间，冲击区局部凹陷，构件下翼缘最大竖向位移为5.03 mm，向内轻微凹陷；速度大于9 m/s时，构件冲击区至外翼缘竖向位移大于16.65 mm，冲击区出现大面积凹陷，构件下翼缘最大竖向位移相近，向内凹陷程度相似；随着冲击物冲击速度增大，冲击物的动能增大，构件变形面积逐渐由冲击点处扩展到整个构件，构件因上翼缘外边缘处和冲击点处发生较大变形失去承载力，构件失效。

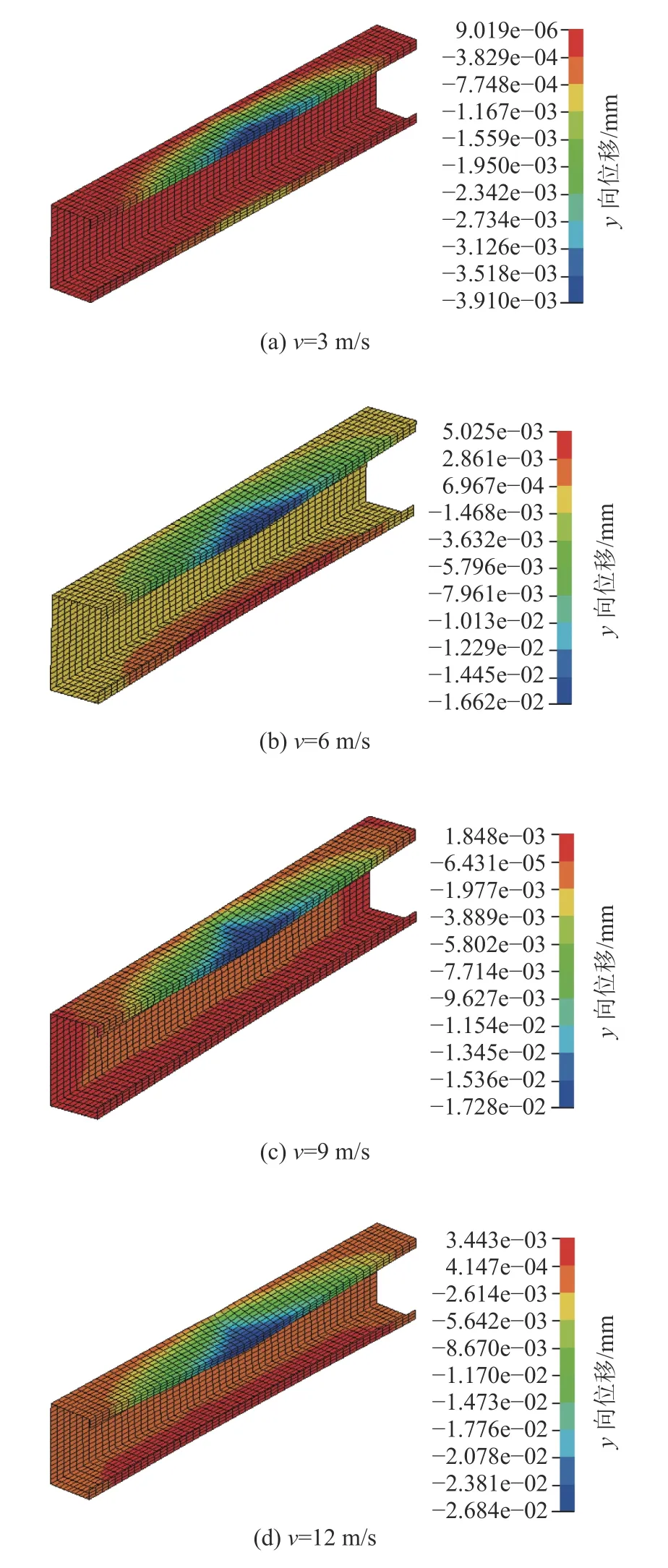
图9 不同冲击速度下的位移云图Fig. 9 Displacement clouds at different impact speeds

4.3 冲击物冲击角度对变形模式的影响

不同角度冲击构件的位移云图如图10所示。

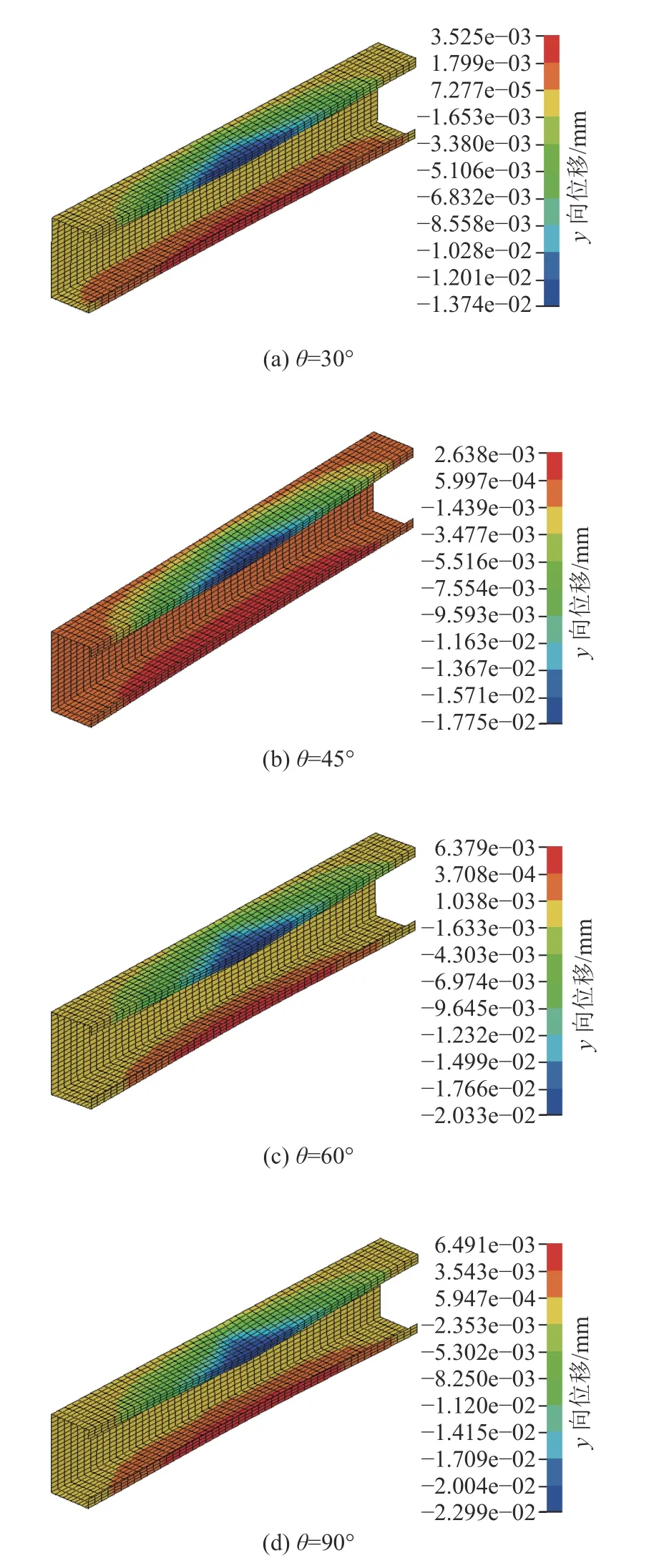
图10 不同冲击角度下的位移云图Fig. 10 Displacement cloud graph under different impact angles

分析图10可得：冲击角度分别为30、45、60和90°时，构件跨中最大位移分别为13.74、17.75、20.33和22.99 mm；随着冲击角度逐步增大，构件的最大位移和变形面积增大；构件最大位移在冲击角度较小时出现在上翼缘外边缘处，冲击角度较大时出现在上翼缘外边缘处和冲击点处；冲击速度一定时，冲击角度不同，构件冲击区的变形不同，冲击物以一定的角度冲击构件时，构件冲击区以一定的角度凹陷，随着冲击角度的增大，冲击能量更多的作用在构件冲击区，构件冲击区的凹陷变形增大；当冲击角度为90°时，位移最大，构件上翼缘外边缘处和冲击点处出现较大变形导致整个构件失去承载力而失效。

5 动力响应分析

5.1 冲击力时程分析

冲击力是由一系列的三角脉冲组成，冲击物冲击C型冷弯薄壁钢构件时，冲击荷载峰值的大小和出现频次的多少代表构件受冲击的强烈程度。冲击力时程曲线如图11所示。

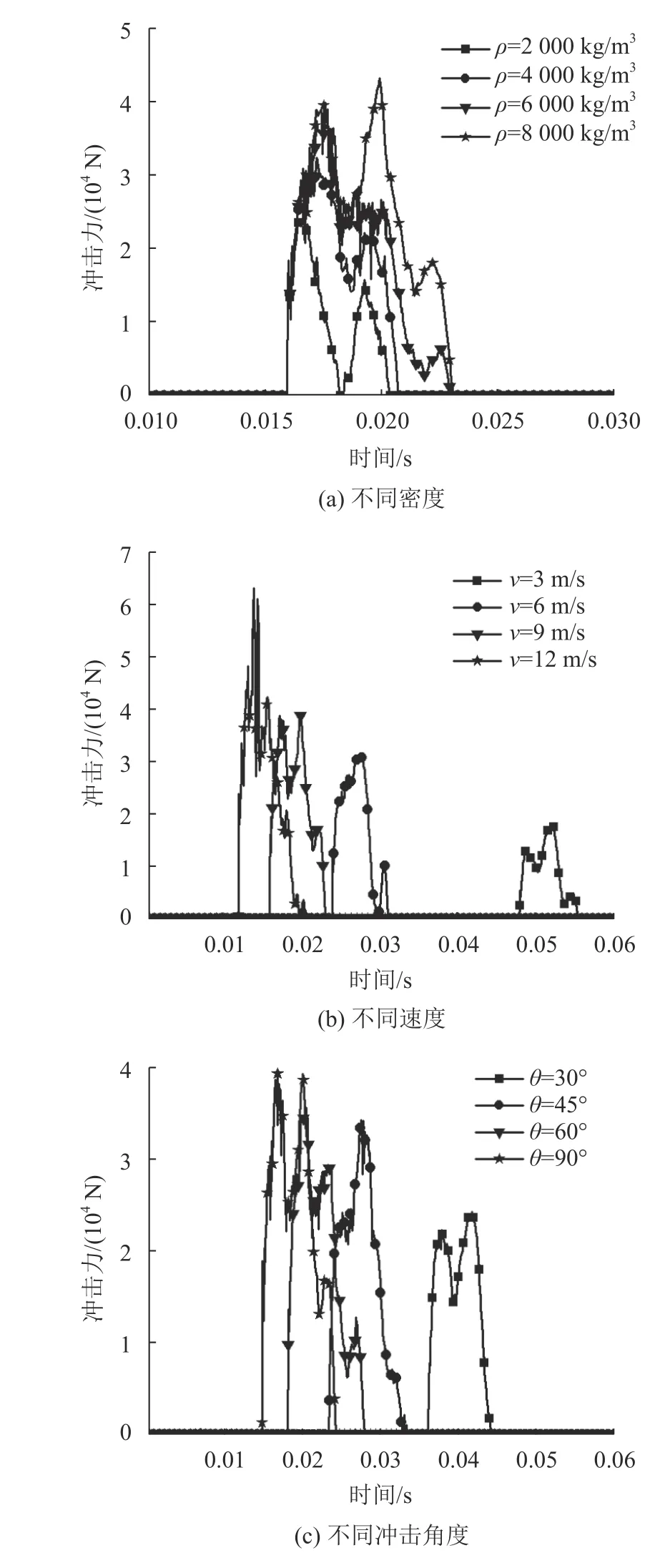
图11 冲击力时程曲线Fig. 11 Impact force time history curves

由图11（a）可得：随着冲击物密度增加，冲击力峰值的大小和频次也在逐渐增加，最大峰值出现时间向后推迟，冲击物和构件的接触时间也有所增加；冲击物密度为2 000至8 000 kg/m3时，冲击力第1个波峰最大值逐渐增大，但增幅逐渐减小，分别为25.5%、15.6%和15.4%，峰值时间从第1个最大波峰转移到第2个最大波峰，由于惯性力增大导致接触时间也有所增加；随着冲击物密度加大，两个主要波峰中间的波谷逐渐变大，冲击物密度为4 000、6 000和8 000 kg/m3时，波谷值分别为14.17、20.47和20.95 kN，表明冲击物密度到达一定值时，改变冲击物密度对构件的冲击力波谷值影响不大。

由图11（b）可得：随着冲击速度增加，波峰和波谷出现的频率和次数增加，冲击力峰值急剧增加，最大增加幅度可达76.6%，峰值出现时间提前，但接触时间变化不大；随着速度的增加冲击能量呈递增趋势，最大峰值点从第2段主要波峰转移到第1段主要波峰；4种不同冲击速度下最小波谷值均大于零，且随着冲击速度的增加，波谷值不断增大，说明速度对冲击力的最大峰值和波谷值影响较大。

由图11（c）可得：冲击角度由30°增加到90°，冲击力时程曲线波峰和波谷出现的频次增加，冲击力最大峰值的增加幅度最大为41.4%；冲击物的冲击角度为90°时，冲击物的大部分初始动能直接传递到构件上，构件的动力响应最为明显。

5.2 位移时程分析

位移是最直观的可以表现构件动力响应的参数，位移振幅的大小和幅度变化的多少反映构件动力响应的程度。当冲击物冲击构件时，位移在瞬间达到极值，构件的冲击点处出现凹陷变形，位移值随后减小到某一稳定值。位移时程曲线如图12所示。

由图12（a）可知：冲击物密度分别为2 000、4 000、6 000和8 000 kg/m3时，构件竖向最大位移分别为7.24、11.54、15.80和20.30 mm；随着冲击球密度的增加，构件竖向最大位移及残余位移明显增大，但增幅减小，达到位移极值及残余位移所需时间增大，表明冲击物密度增大，惯性力增大，导致构件产生的变形增大，冲击物反弹所需时间增长。

由图12（b）可知：冲击速度增加，即冲击物能量增大，构件需要产生更大的变形来消耗巨大冲击能，冲击作用产生的位移极值和残余位移相应变大；与此同时，冲击速度增大导致冲击物与冲击构件接触时间缩短，位移峰值出现的时间不断提前，但最大位移与冲击速度之间并不是单一的线性关系。

由图12（c）可以得出：冲击物冲击角度分别为30、45、60和90°时，竖向位移最大值为8.65、12.59、16.18和20.09 mm。冲击角度增幅不同，但竖向位移最大值增幅值基本相等，位移极值出现的时间不断提前。

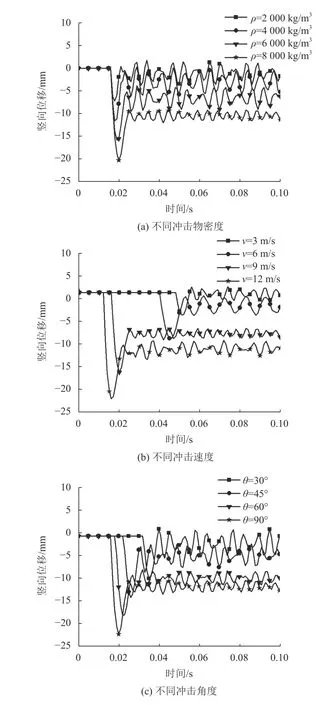
图12 位移时程曲线Fig. 12 Displacement time history curves

5.3 能量分析

根据机械能守恒原理，冲击物的初始动能转化为构件的应变能和冲击物反弹所需动能。整个冲击过程能量的主要能量形式为应变能和动能。其中，应变能以钢梁构件凹陷变形的形式储存在构件中，动能以冲击物反弹的形式出现。以冲击物速度为3 m/s时的能量时程曲线为例的能量时程曲线如图13所示。

图13 能量时程曲线Fig. 13 Energy time curves

分析图13可得：总能量为冲击物冲击钢梁构件的初始动能，由于冲击物冲击钢梁构件的过程中摩擦消耗小部分能量，总能量略微减小；冲击物的总能量转化为构件的应变能在0.052 s达到应变能最大值53.77 J，随后立即减小至稳定值15.15 J；冲击物冲击钢梁后发生反弹带走一部分的能量。

当钢梁构件受到冲击荷载作用时，应变能以构件发生变形的形式储存在构件的内部。图14为不同冲击物密度、不同冲击速度和不同冲击角度下的应变能曲线。

由图14（a）可知：随着冲击物密度逐渐增加，应变能峰值逐渐增加，应变能达到峰值的时间大致为0.02 s；应变能在达到峰值后立即趋于稳定，应变能稳定值随着冲击物密度增加而增加，但应变能稳定值占应变能峰值的比例保持在60.0%左右；增加冲击物密度改变冲击物的冲击动能，钢梁的变形程度增大，应变能峰值和稳定值相应增大，但对应变能稳定值占应变能峰值的百分比影响不大。

由图14（b）可知：随着冲击物冲击速度的逐步增大，冲击物冲击钢梁构件的时间提前，构件受冲击后应变能立即达到最大峰值，随后达到应变能稳定值；随着冲击速度的增加，应变能峰值和稳定值增大，应变能稳定值占应变能峰值的百分比增大，构件冲击区的变形程度明显增大，表明改变速度参数对构件的变形破坏和应变能影响较为显著。

由图14（c）可得：随着冲击构件的冲击角度逐渐增加，应变能达到峰值的时间提前，应变能峰值和稳定值不断增大，但应变能稳定值占应变能峰值的百分比基本稳定在60.0%～70.0%之间，当冲击物冲击角度为90°时，应变能峰值和稳定值达到最大，对构件的破坏最严重。

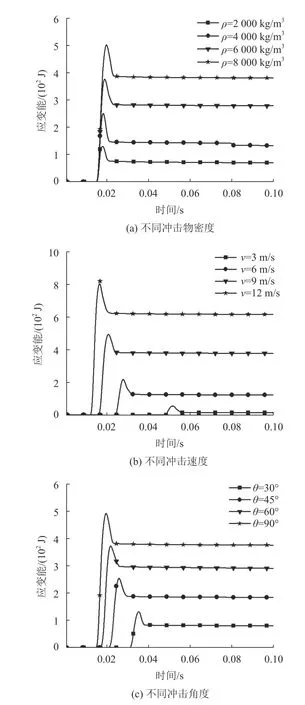
图14 不同参数下的应变能曲线Fig. 14 Strain energy curves under different parameters

6 结 论

通过对C型冷弯薄壁槽钢梁在低速横向冲击作用下动力响应的研究，得出以下结论：

1）采用ANSYS有限元软件建立了C型冷弯薄壁槽钢梁的数值分析模型，得到的位移云图、位移极值与冲击试验所得的结果相比有较好的吻合性，验证了有限元数值模拟的有效性。

2）根据构件最终的变形形式以及构件冲击区的凹陷程度，冲击荷载作用下构件的变形模式为：构件冲击区轻微凹陷、构件冲击区局部凹陷、构件冲击区大面积凹陷。

3）随着冲击物密度增大，构件的冲击力峰值逐渐增大，但增大的幅值逐渐减小，构件的最大竖向位移逐渐增大，且达到位移最大值的时间基本相同；随着冲击速度增大，构件冲击力峰值与冲击力波谷值逐渐增大，峰值增加的最大幅度为76.6%，构件竖向位移逐渐增大；随着冲击物冲击角度的增加，构件的冲击力峰值逐渐增大，增加的最大幅度为41.4%，构件竖向位移逐渐增大，且成比例增加。