非线性波作用下潜堤周围的流体分离与涡流结构

蒋学炼，刘 畅，赵 悦，杨伟超*，柳淑学，朱福明

(1.天津城建大学 天津市软土特性与工程环境重点实验室，天津 300384；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3.天津市北洋水运水利勘察设计研究院有限公司，天津 300452)

作为兼具观赏性和防护性以及水体交换功能的潜堤，近年来在海岸工程领域得到了广泛的应用，其水力性能的研究也成为热点问题之一[1–2]。目前，随着实验技术和计算流体力学的发展，研究人员开始尝试从流场结构角度解析潜堤的水力性能。

Lin等[3]联合运用激光诱导荧光（laser induced fluorescence，LIF）技术、粒子图像测速（particle image velocimetry，PIV）技术、质点追踪（particle tracing，PT）技术考查了孤立波作用下矩形潜堤周围的紊动射流现象。刘彦等[4]基于PIV图像研究了不同流速下单体及双体人工鱼礁周围的上升流和背涡流特征。Qie等[5]采用PIV技术在多种型式的潜堤周围捕捉到交替泻放的漩涡，并证实其是造成不同堤型反透射特性差异的重要原因。Zarruk等[6]运用染料示踪法追踪了孤立波作用下同轴双圆柱潜体附近的涡流演变过程，认为涡流的生成和泄放会造成动水压力梯度的变化，从而影响建筑物所受到的波浪荷载。Athanassios等[7]基于2D–PIV量测数据分析了块石护面陡坡的波生流场，探讨了波浪爬坡过程中的流体分离和紊流场演变过程。Na等[8]联合PIV技术和光纤反射仪（fiber optic reflectometry，FOR）研究了崩破波的破碎过程及能量转换规律。可见，日趋精密的非接触式实验技术已经能够在不干扰流场的前提下有效捕捉微观流动结构。

相比于模型实验，计算流体力学（computational fluid dynamics，CFD）以其费用低、无比尺效应、可知悉流动细节的优点，成为波浪与建筑物相互作用研究领域的有力辅助工具，如相对干舷高度对矩形潜堤涡量场的影响[9]、斜坡堤后越浪水体的空间分布[10]、不同潜堤背面动水压强的分布差异[11]、越浪水池式防护建筑物的越浪量[12]以及椭圆余弦波与弧形潜堤的相互作用[13]等。

上述研究多采用规则波、孤立波或椭圆余弦波，分别对应深水和浅水工况，且未考虑抛石基床，而多数潜堤建设在过渡水深区域，由抛石基床支撑，其常规工况非线性的斯托克斯波形更适用。为此，本文执行了斯托克斯2阶波与抛石基床矩形潜堤相互作用的PIV试验，获取了迎浪区域和背浪区域的波面过程和速度场，展示了潜堤周围不同相位时刻的涡流结构。基于RANS–VOF格式建立了与试验对应的数值模型，探讨了不同造波方法的适用性和海绵层的消能效果，进一步分析了潜堤表面边界层的流体分离现象。

1 试验设计

试验在大连理工大学海岸和近海工程国家重点实验室开展，波浪水槽长30.00 m，宽0.40 m，高0.65 m，一端装有液压推板式造波机，另一端设消能斜坡（图1（a））。水槽底部和侧面均为可透光的有机玻璃。模型堤体采用丙烯酸有机玻璃制成，放置于水槽中部抛石基床上，高度0.175 m，顶宽0.200 m，内部铅块配重。在后续分析中，设定迎浪堤脚为坐标轴原点(x= 0，z=0)，水平轴顺波形传播方向为正，垂直轴向上为正。

距离迎浪堤面和背浪堤面10 cm处分别放置2支浪高仪（WG–F、WG–R），用于波浪越堤过程中的波面变形分析，波面的采样频率为50 Hz。采用PIV技术捕捉潜堤迎浪面和背浪面的瞬时速度场，采样区域设置在基肩上方见图1（a）中的FOV–F和FOV–R（field of view，FOV），宽度为25.5 cm，高度为18.5 cm，对应的分辨率为57 像素/cm。数字电荷耦合摄像机（CCD）安设于水槽侧面采集PIV图像，光源由安设于槽底下方仪器室的双头钇铝柘榴石晶体谐波激光器提供，脉冲延迟400 ms，经柱面镜散射后透过玻璃槽底和基床狭缝形成双倍频片光点亮测速区域（见图1（b））。激光器触发和CCD相机采集由信号同步器控制同步。采用INSIGHT–3G软件对连续采集的PIV图像序列进行多通道互相关分析，在x方向和z方向分别设置48个和35个速度矢量点，采样精度为每厘米1.8个速度点，每帧图像获取1 680个网格点的瞬时速度矢量值。PIV采样频率为15 Hz，每次采样的两帧图像之间的时间延迟为600 ms。

图1 试验布置Fig. 1 Experiment configuration

选择一种代表性的潜堤工况，试验水深h=0.333 m，波高H=0.068 m，周期T=0.996 s，波长L=1.4 m。根据le Méhauté[14]的波浪理论适用范围判断，试验波形为斯托克斯2阶波。参考流速取淹没深度（d=0.083 m）处的斯托克斯2阶波水质点水平速度幅值，即：

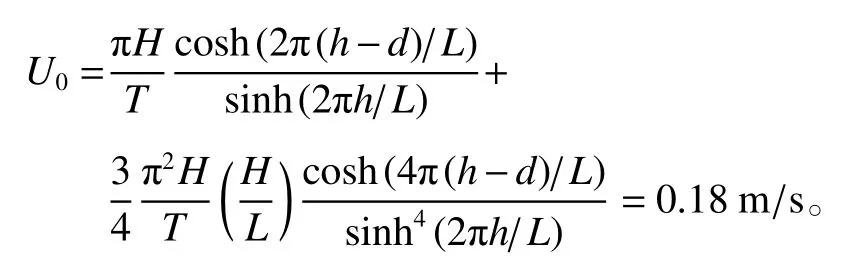
基于可靠性考虑，试验重复3次，自第6个稳定波峰通过各采样区域中心位置正上方时开始采样，采集总时长10 s，包含10个完整波浪周期。每次试验前在测速区域放置水下标定尺，获取相机成像像素和片光源位置平面尺寸之间的比例，用于PIV图像分析中网格点瞬时速度值的参考基准。示踪粒子为平均粒径10 µm的聚氯乙烯粉末，均匀掺混于水槽的模型段，以提高速度捕捉的灵敏度。

2 试验结果

2.1 波面

图2展示了有无潜堤情况下的波面过程。

图2 波面的时间历程Fig. 2 Temporal variation of surface elevations

由图2（a）显示空槽波面与入射波面吻合良好，空槽波高和波周期的均方根偏差均值分别为0.214 2和0.007 5，说明试验波形稳定。由图2（b）可以看出，越堤前后的波面均发生了非线性变形。引入不对称度（asymmetry）和偏度（skewness）衡量波面的变形程度[15]：

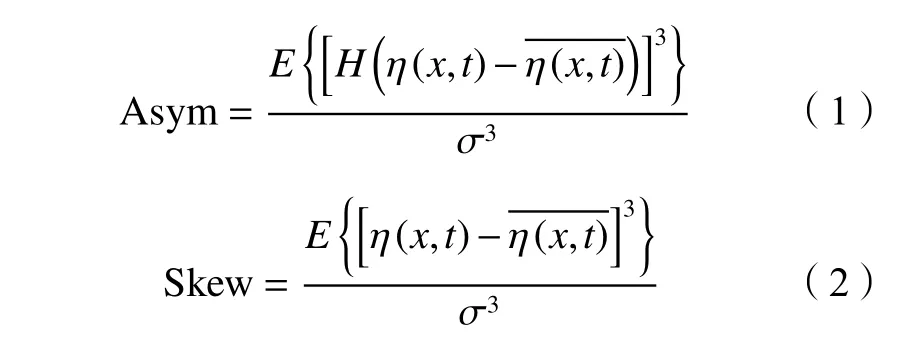
式中： η (x,t)为x位置处t时刻的波面高程； η(x,t)为波面高程均值；H(·)表 示Hilbert变换；E(·)表示均值算子；σ为波面高程的标准差；不对称度 A sym表征波浪形状相对于垂直轴的不对称程度，为负值时代表波面前倾（即波峰相对于垂直轴左偏斜），为正值时代表波面后倾（即波峰相对于垂直轴右偏斜）；偏度Skew表征波浪形状相对于水平轴的不对称程度，为正值时代表波峰上抬，波谷坦化，为负值时代表波峰下降，波谷尖化。

理论入射波面的不对称度为 − 3.29×10−5，偏度为0.23。与之相比，迎浪面的波形变化幅度较小，不对称度和偏度分别为–0.21和0.04，由于潜堤的阻水效应，其波面更为前倾。背浪面的波高减小幅度较大，说明部分波能在越堤过程中损耗，同时图2中出现了次生峰谷，表明部分波能从低频向高频转换，产生了高次约束谐波和自由谐波。背浪面波形的不对称度和偏度分别为–0.39和0.99，相对于垂直轴和水平轴均表现出明显的不对称性。越堤过程中的波面非线性变化与潜堤附近的流场紊动有关，后续将从涡流结构角度进行分析。

2.2 速度场

基于PIV速度场分析波浪越堤过程中的涡流结构。以波面通过各采样区域正上方为准，一个周期内定义8个特征相位时刻（图3），其中相位1对应波峰时刻。

图3 一个周期内波面的相位时刻示意Fig. 3 Sketch of surface elevation phases within a wave period

图4呈现了一个周期内迎浪采样区域（FOV–F）和背浪采样区域（FOV–R）在不同相位时刻的速度场（矢量图）和涡量场（云图）。为了消除试验过程中的波动，采用经过相平均的速度场和涡量场，其计算式为：

由图4可见：相位1时刻，波峰越堤，潜堤顶面射流通过背浪堤角发生流体分离，生成顺时针负涡（图4中A区），与正向水流从迎浪面携带来的逆时针正涡形成涡对（见相位8）。扩散过程中，顺时针负涡向下游和底部对流，而逆时针正涡则向自由液面传递（相位2～相位3）。由于波浪的周期性运动，这一反向旋转的涡对并不能充分发展，从相位4时刻开始，反向水流增强了逆时针正涡，顺时针负涡开始拉伸分解，到相位7时刻基本耗散为小尺度涡旋。背浪区域的主涡对主要局限于距离堤背约1倍Keulegan–Carpenter数范围（0.54h≈17.9 cm）内。在整个周期过程中，背浪基肩上的涡量均很小，可视为紊流遮蔽区，工程中存在淤积的可能（图4中B区）。

相位5时刻，波谷越堤，反向水流携带背浪侧的逆时针正涡扫过迎浪堤角，叠加迎浪堤角处的剪切边界层流体分离，生成了一个强逆时针正涡，并在迎浪堤面侧诱导出一个顺时针负涡（图4中C区）。这一涡对的运动方式不同：逆时针正涡基本维持在迎浪堤角附近；而顺时针负涡则顺着堤面向底床传递拉伸（相位6～相位7）；到相位8时刻，水流转向，涡对随正向水流向堤背传递。相对于背浪区域，迎浪堤角的主涡对运动范围更窄，局限于距离堤面约0.5倍Keulegan–Carpenter数的范围内（ 0.5×0.54h≈9.0 cm）内。与堤背不同的是，相位4时刻迎浪基肩上生成一个小型涡对（图4中D区），随后在上升水流和正向水流作用下向液面和下游对流扩散，逐渐分解破碎，影响范围约两个水质点运动轨迹（2S=6.4 cm）。这一涡对的运动范围较小，可能引起局部冲刷。

图4 不同相位时刻的相平均速度场和涡量场Fig. 4 Phase-averaged velocity and vorticity fields at different phases

3 数值模型

为了理解涡流的生成机理及其相互作用，采用数值模拟进行更深入的研究。

3.1 RANS–VOF架构

数值波浪水槽采用RANS–VOF架构，水流运动控制方程为描述不可压缩黏性流动的雷诺时均纳维尔–斯托克斯方程（Reynolds–averaged-Navier–Stokes equations，RANS）：

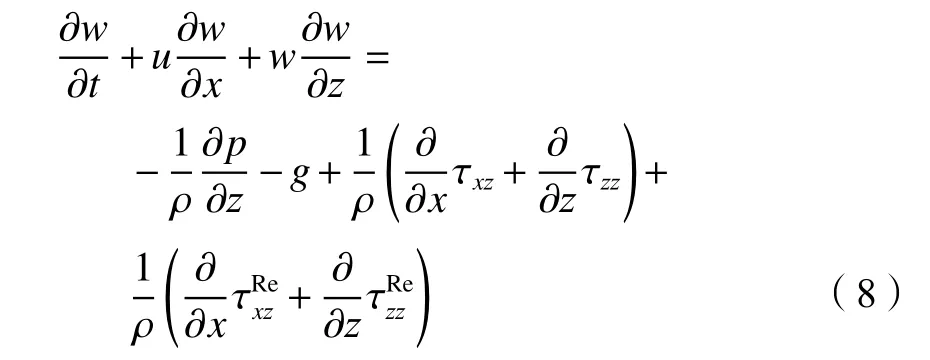
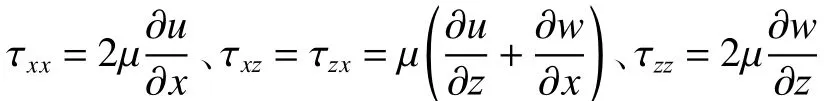
抛石基床内的流体运动采用空间平均的纳维尔–斯托克斯方程控制[17]：

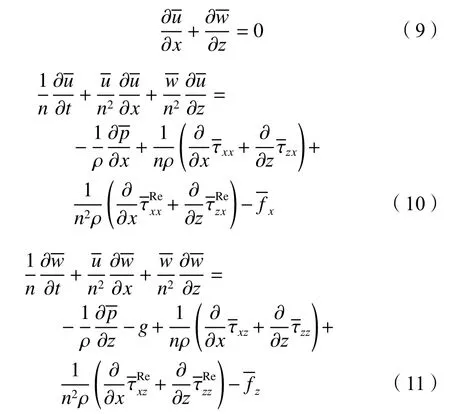
波浪运动过程中的自由液面采用流体体积分数法（volume of fluid，VOF）追踪[18]：

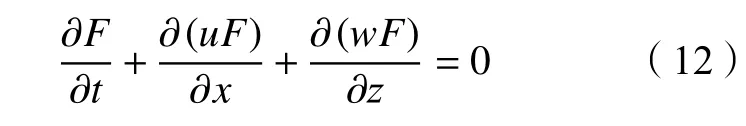
式中，F为各计算单元内的流体体积分数。

上述RANS–VOF架构采用有限差分离散、两步映射法求解，详细过程参考文献[19–20]等。这一数值模式已应用于众多波浪与建筑物相互作用问题中，如护面块体消浪能力[21]、弧形堤波浪荷载[22]、直立堤前冲刷[23]等。

3.2 数值造波

常用的数值造波方法包括边界造波、动板造波和源函数造波3种。边界造波法[24]根据目标波形指定入流边界的速度和波面时间历程，通过动量传递实现数值造波。动板造波法[25]根据目标波浪要素确定动板的速度时程，通过造波板的往复强迫运动引起水体波动。上述2种方法适用于弱反射或反射波能够事前估计的情况，当RANS水槽内有建筑物且二次反射较强时，即使引入吸收式造波技术，长时间模拟后也可能累积较大的数值误差。源函数造波法[26]是在水流连续性方程或动量方程中增加质量源项或动量源项，通过源域往复释放吸收质量或动量形成水体波动，由于入射波和反射波分别从两端开放边界流出，可有效消除二次反射影响。

本文选用质量源函数造波法。源域内的连续性方程（6）改写为：

式中，S(x,z,t)为 质量源函数，Ω代表源域。

当源域宽度相对于目标波长很小时，质量源函数S(x,z,t) 与源域正上方的目标波形 η(t)之间的关系为：

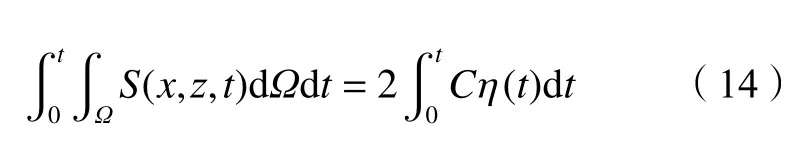
式中，系数2表示质量源同时产生传播方向相反的两列波，C为目标波速， η (t)为目标波面方程。

由斯托克斯2阶波的波面方程可推导出质量源函数的表达式：

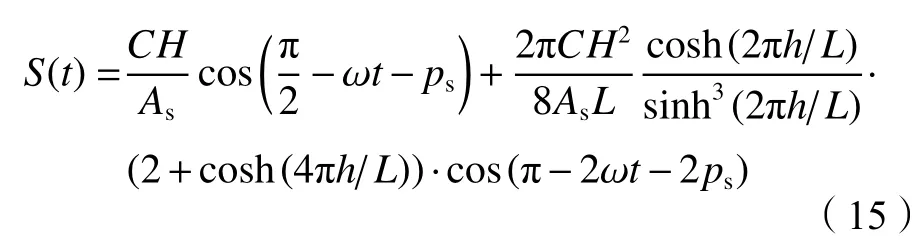
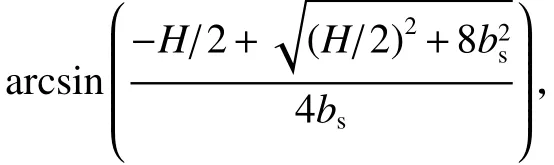
丁阳等[27]建议将质量源函数乘以一个递增的包络系数，使前3个周期的波面逐渐增大，以避免初始计算阶段源域上方产生过大波动影响波面的稳定性，包络系数R的表达式为：

对于非线性波，在开放边界处仅采用辐射边界难以完全透射波能。为了减小边界反射，基于人工衰减消波的思路，本文在开放边界前部设置海绵层消浪。在海绵层内，水平向动量方程（7）修正为[28]：

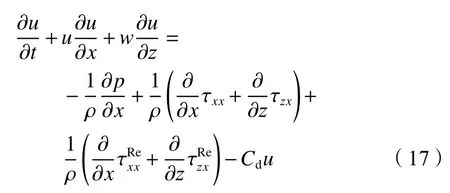
式中， −Cdu为人工阻尼项，其中，Cd为阻尼系数，顺海绵层由0线性增长到1.0。

3.3 模型验证

3.3.1 波面

图5比较了试验波面和3种造波方法得到的数值波面。分别采用不对称度、偏度、相关系数、欧式距离衡量波形的相似度和波面过程的累积偏差，如表1所示。其中，欧式距离公式见式（18），用于衡量试验波面与数值波面的累计偏差。综合比较可知，源项造波的数值波面与试验波面的相似度最高，累积偏差最小。

表1 数值波面与试验波面的波形参数Tab. 1 Parameters of numerical and experimental wave profiles

图5 数值波面与试验波面比较Fig. 5 Comparison of numerical and experimental surface elevations

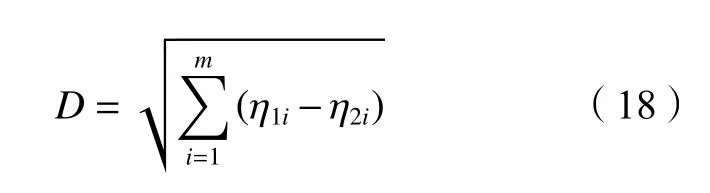
式中，η1i为 试验波面，η2i为数值波面。

3.3.2 速度场

图6比较了迎浪面2个特征时刻瞬时速度场的PIV实测数据和数值模拟结果。从图6整体来看，数值结果与PIV实测结果吻合良好。由于分辨率的限制和数据平滑处理，少量区域的PIV测速结果不如数值结果平顺，表明数值模型可以更精细化地模拟建筑物附近的流场。

图6 瞬时速度场PIV实测和数值模拟结果比较Fig. 6 Comparison of instantaneous velocity fields results captured by PIV and numerical simulation

图7比较了迎浪堤脚和背浪堤脚2个特征时刻的水平速度幅值沿水深的分布。由图7可知，数值结果与实测数据的分布趋势和量值均吻合较好。此外，可以看出，由于涡旋引起的动量掺混，流速的分布并不符合理论的抛物形，而是趋向于均匀分布。

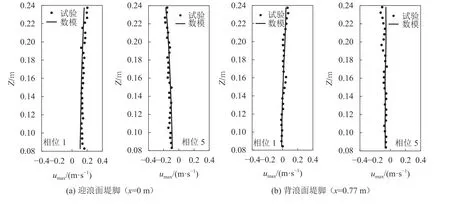
图7 水平速度幅值的垂向分布Fig. 7 Vertical distribution of horizontal velocity amplitudes

上述验证表明，本文构建的RANS-VOF数值波浪水槽可以较准确地模拟非线性波浪与矩形潜堤的相互作用。

3.4 流体分离分析

基于数值速度场分析波浪越堤过程中边壁附近的流体分离现象（图8）。以波面通过潜堤质心正上方为准，参照图3定义特征相位时刻。 图8中，涡量色条下为自由液面的涡量等值线，由于波浪越堤过程中的浅化效应，发生了部分破碎，故波面始终存在小尺度涡旋。其下域中的符号A、B、C、D分别指代背浪堤角和壁面、后趾、迎浪堤角和壁面、前趾4个结构区域。

图8 近壁区涡量场的演变Fig. 8 Evolution of vorticity field in near-wall regions

由图8可知：相位6～相位8时刻，一个新的波到达堤顶，C区的剪切边界层内开始生成负涡量，并向上部发展。相位1～相位2时刻，波峰通过潜堤上方，C区剪切边界层内的顺时针负涡从结构表面泄放，向自由液面和下游拉伸、对流，迎浪堤角边界层内开始诱导出反向旋转的正涡量，同时，堤顶负涡边界层逐渐发展并向背浪堤角传递。相位3时刻，水流开始反向，结构表面正涡剪切层逐渐发展。到相位5时刻已占满堤顶表面，切断了顺时针负涡的涡量供应，并在迎浪堤角从结构表面泄放出逆时针正涡，向底床和上游拉伸、对流，但这一过程并没有充分发展，随着正向水流的到来，逆时针正涡转而向自由液面运动，并与之相互作用。同时，迎浪堤角泄放出的顺时针负涡进一步向自由液面传递，与之发生强烈的相互作用而耗散；背浪面A区的顺时针负涡也从结构表面泄放，向底床拉伸弯曲，随后在反向水流的作用下与潜堤表面的正涡边界层相互作用而耗散。在一个周期循环中，前趾D区的涡旋变化过程与C区类似，存在一个小型环流系统，后趾B区的涡旋强度则始终较弱。

图8表明，随着波浪越堤过程中的水流周期性变化，迎浪面C区和背浪面A区的剪切边界层内交替生成负涡量和正涡量，其生成机理可用图9解释。

图9 剪切边界层内反向涡量的生成机理（相位8）Fig. 9 Formation mechanism of reverse vorticity in shear boundary layer (phase 8)

以相位8时刻迎浪堤面生成负涡量为例，堤角处边界层流体分离泄放出的逆时针正涡随着正向水流的到来向结构物附近传递，使得迎浪面近壁区流体减速，动水压力增大，形成自下而上的逆压梯度和抽吸效应，将水体加速推向堤角上部，在高低压之间的剪切边界层内诱导出负涡量。

4 结 论

采用PIV技术和数值模拟研究了非线性波与矩形潜堤相互作用过程中的涡流结构和流体分离，得到如下结论：

1）越堤过程中的波面非线性变化与潜堤附近的流场紊动有关。迎浪区域的主涡对运动范围较窄，波能损耗小，波形变化幅度较小，背浪区域的主涡对扩散范围较大，波高减小幅度较大，部分波能在越堤过程中损耗，部分波能从低频向高频转换，产生了高次约束谐波和自由谐波，波形相对于垂直轴和水平轴均表现出明显的不对称性。

2）在波浪作用下，反向旋转的涡对在迎浪面和背浪面周期性地生成、泄放和传递，但均未能充分发展，由随后到来的变向水流携带，与自由液面或结构表面相互作用而耗散。数值模拟结果表明，涡旋的涡量供应主要来自结构表面的剪切边界层，而这些反旋涡量是由分离涡运动引起的逆压梯度诱导生成的。

3）目前的工程设计主要基于无黏势流理论，未考虑涡旋引起的复杂流动效应，但研究结果表明涡旋的生成、泄放、拉伸、对流、耗散会显著改变局部流场，进而影响结构物的局部冲淤和受力。RANS–VOF数值波浪水槽为潜堤周围涡流效应的精细化研究提供了一种有效工具，可用于波浪与潜堤相互作用的参数分析和工程设计方案优化。[致谢] 衷心感谢赫瑞瓦特大学（Heriot–Watt University）的Zou Qingping教授为本文工作提供的技术指导，衷心感谢四川大学的林鹏智教授为本文的数值模拟工作提供的RANS–VOF源代码。