夯基固本 回归本质——2020年全国卷Ⅰ理科数学18题解析

>>>范倩楠

(审稿：何柏林)

(本文责编：赵宁宁)

立体几何是高中数学的重要模块之一.包括“空间几何体”“点、线、面的位置关系”“空间向量和立体几何”等几部分。高考立体几何解答题具有较强的综合性.重视基础知识、基本技能和创新意识的考查.突出直观想象、逻辑推理、数学运算等学科核心素养的检测.多数采用“一问证明、一问计算”的呈现方式.第一问主要考查点、线、面位置关系的证明.第二问涉及角与距离或体积的计算。本文对2020年全国卷Ⅰ理科第18题的答题情况进行分析.以期对立体几何的备考提供参考。

一、高考原题

【2020年全国卷Ⅰ，理科数学18题】

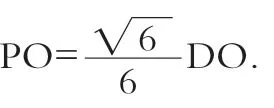
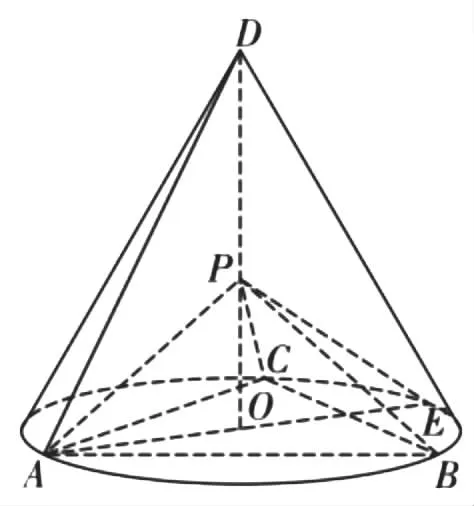
(1)证明：PA⊥平面PBC；

(2)求二面角B-PC-E的余弦值.

解法示范：

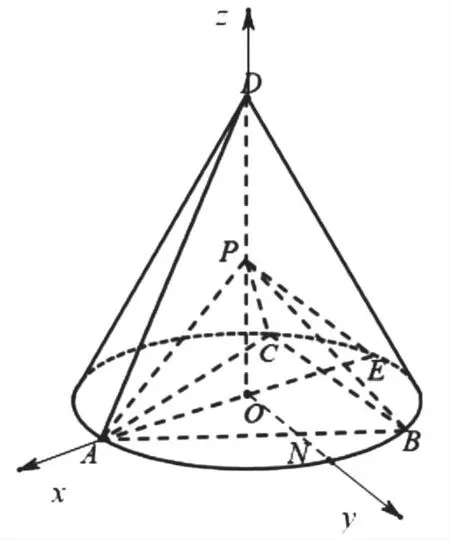
(1)由题设知，△DAE为等边三角形，设AE=1，

同理PA⊥PC，又PC∩PB=P，所以PA⊥平面PBC.

二、错例典析

1.逻辑推理欠规范

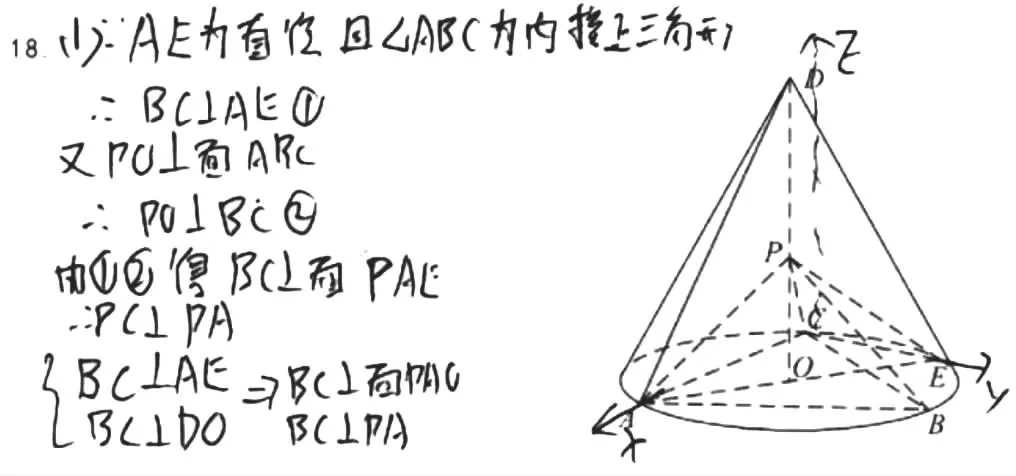
2.空间直角坐标系建立不妥当

3.运算出错

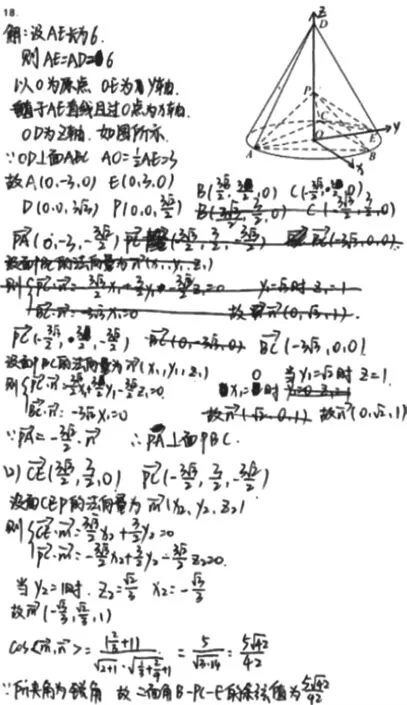
三、备考建议

1.回归教材

教材是落实学生数学核心素养的重要资源.也是历年高考命题的重要素材。在立体几何的教学中.要学会从课本的基本立体图形中.发现和探索直线、平面平行(垂直)关系的判定和性质。要善于从一般到特殊.从线到面再到体.完善立体几何的研究路径.践行立体几何的研究方法.从而发展学生直观想象的数学素养。

2.重视“基本图形”的作用,形成完善的知识与思想方法体系

对于学生来说.总感觉立体几何图形线条多.又处在不同平面内.难以发现要素之间的关系。实际上.空间图形总有一些简单的“基本图形”.教学中应重视基本图形的作用.立足从“基本图形”到“变式图形”再到“综合图形”.就能形成完善的知识与方法体系。

3.规范书写,发展逻辑推理的数学素养

学生在立体几何题解答过程中存在两个突出问题:一是证明过程表述不规范.甚至是主观臆断；二是使用向量方法时经常出现计算错误.将相应点的坐标、向量坐标或平面的法向量求错.导致失分。因此.对立体几何定理性质的学习.在重视理解的同时还要强化表述和记忆.特别是“三种语言”——文字语言、符号语言、图形语言之间的转换。文字语言有助于记忆；符号语言有助于推理过程的正确书写；图形语言有助于从复杂问题情境中提取定理的基本模型。

4.重视向量法的过程性教学

利用向量法快速准确解决立体几何问题的关键是建立合适的空间直角坐标系。常用方法有:

（1）利用共顶点互相垂直的三条棱建立空间直角坐标系.如图1；

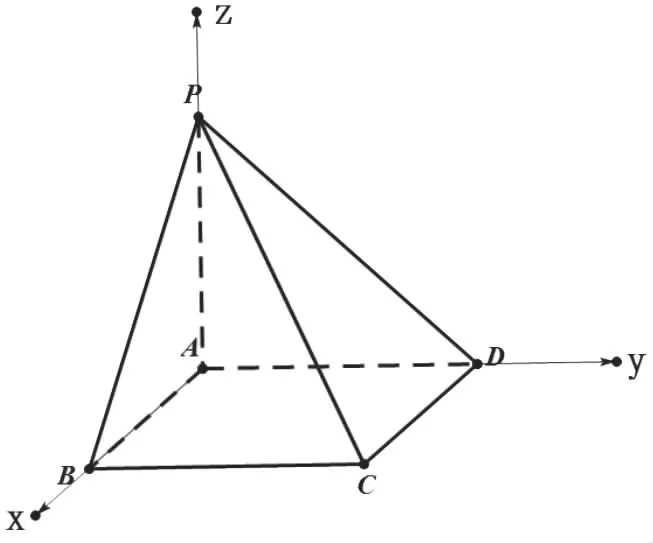
图1

（2）利用线面垂直关系建立空间直角坐标系.如图2；

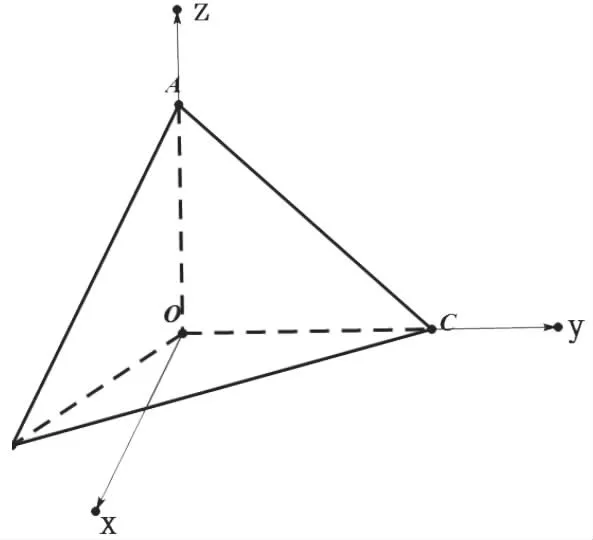
图2

（3）利用面面垂直关系建立空间直角坐标系.如图3；

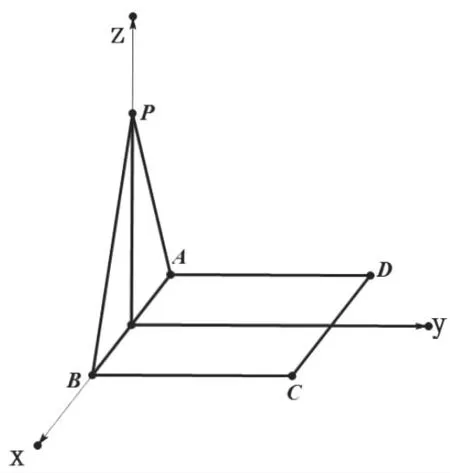
图3

（4）利用正棱锥的中心与高所在直线建立空间直角坐标系.如图4。

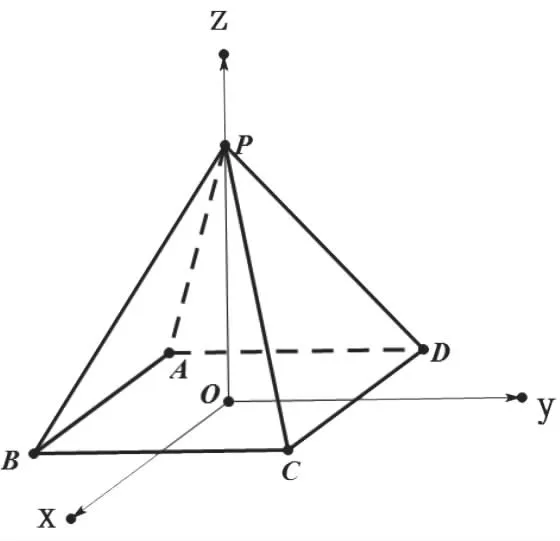
图4