山重水复疑无路,柳暗花明又一村
2021-10-16李子奇
李子奇


中图分类号:A 文献标识码:A 文章编号:(2021)-33-426
在初中数学中,一些概念往往看似简单,但学生不能正确地理解概念,更不能灵活地应用所学概念解决问题,其原因主要是因为学生的天性倾向于依赖直观和具体。特别当情景或图形发生变化时,他们不知所措,无法用所学知识进行分析问题,解决问题。因此,数学概念的教学,教师要挖掘教材,引导学生从表面到本质理解概念的内涵与外延,把握概念的深层结构,要善于掌握更多的典型、精彩的例子,深刻探究概念的“七十二般变化”,只有这样,才能引领学生充分地理解概念的核心部分,掌握一定的分析方法,数学学习才能高效。
本文通过“对同位角、内错角、同旁内角”的概念教学,说明如何挖掘概念的核心部分,突破教学难点。
人民教育出版社《数学》七年级下册,第五章 相交线与平行线中,第三节内容为“同位角、内错角、同旁内角”。教材通过具体图形给出了“同位角、内错角、同旁内角”的概念,看似简单、具体、明了。实际上,经过几年的教学经验发现绝大多数同学不能正确地理解这三个概念,所做的习题一塌糊涂,只是想当然的进行判断。
在教学探究中不难发现,无论是同位角、内错角、还是同旁内角的两个角,它们的共性是,两角的四条边中,有两条边所在的直线是同一条直线,实质上这条直线就是第三条直线,其余两条边所在的直线就是第一、二条直线。因此,教学过程中指导学生寻找出两个角的四条边,根据特定图形观察找出两个角的公共边,即第三条直线,就能顺利而正确地判断哪两条直线被第三条直线所截,再根据两个角在第三條直线的两侧或同侧,与第一、二条直线的位置关系,就能轻而易举地得出两个角的位置关系。
例1、 如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的?它们各是什么角?(人民教育出版社七年级《数学》下册,第9页第11题)
分析:在图(1)中,∠1是由DB和DC两条直线组成的角;∠2是由DB和AB两条直线组成的角;在四条直线中,DB重合则是第三条直线,即∠1和∠2是DC和AB两条直线被DB所截;又因为∠1和∠2分布于DB两侧,在AB和DC之间,所以是内错角。
在图(2)中,∠1是由DC和CB组成,∠2是由AB和BC组成,重合的直线是BC,即BC是第三条直线,而∠1和∠2分布于BC的同侧,在DC和AB之间,因此,它们是DC和AB被直线BC所截得到的同旁内角。
在图(2)中,∠3是由AD和AB组成,∠4是由BC和BE组成,而AB和BE是同一条直线,即它们是AD和BC被AE所截得到的同位角。
能正确判断对同位角、内错角、同旁内角,就很容易掌握平行线的性质及判定。
例2、如图,BE是AB的延长线,(1)由∠CBE=∠A可以判定哪两条直线平行?根据是什么?(人民教育出版社七年级《数学》下册,第15页,练习第1题)
分析:由角的关系要判断直线的位置关系,实质上也是判定哪两条直线被哪一条直线所截,第一、二条直线就有可能是平行线。
因为∠CBE是由BC和BE组成,∠A是由AD和AB组成,而AB和BE是同一条直线,即是第三条直线,故说明BC和AD被AE所截,又因为∠CBE=∠A是同位角且相等,所以AD∥BC
以上,同位角、内错角、同旁内角的判断相比较容易,关键是图形背景和教材上所学概念时的图形很相近,用这种方法去判断显得比较麻烦,可是当图形背景变化时,方能显出这种方法的优越性和用武之地。
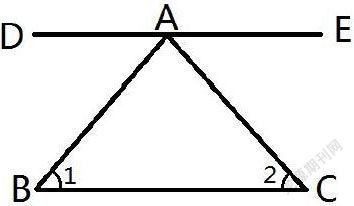
例3、如图,∠1与哪个角是内错角,与哪个角是同旁内角?∠2与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?(人民教育出版社七年级《数学》下册,第7页,练习第2题)
分析:∠1是由AB和BC组成,当AB为公共边时,即AB是第三条直线,从图中可以看出AB既是∠DAB的一条边,又是∠BAE的一条边,因此,DA和BC被AB所截∠1和∠DAB是内错角,∠1和∠BAE是同旁内角;当BC为公共边时,则BC又是∠BCA的一条边,因此,AB和AC被BC所截,且∠1和∠2是同旁内角;
同理,可以分析∠2的内错角与同旁内角。
顺便一提,我觉得这道题不适宜作为练习题,应该安排在习题的拓展探索部分中,因为,这道题显然并不简单。
课堂教学中概念和方法是学习过程中一个重点,是走向知识深处的一支撑点,而数学概念的教学理解又是一个永无止境的过程,因此,希望我们广大数学教师在数学概念的教学理解上下一番苦功,掌握从大量知识中汲取促进数学教学营养的能力,从而使自己进入数学教学的自由王国。
