加劲钢桁连续刚构桥地震易损性分析
2021-10-16李庞
李 庞
(中铁六局呼和浩特铁路建设有限公司,内蒙古 呼和浩特 010050)
0 引言
桥梁作为交通路网中的连接构件,是保证交通顺畅和经济发展的关键组成部分,桥梁结构在地震作用下发生损伤,会严重影响社会和经济发展,所以桥梁的地震损伤分析具有举足轻重的意义。大跨度连续刚构桥由于其外观优美、克服复杂地形能力强等优点,在交通路网建设中被广泛应用,同时,由于其后期保养难度高,对其抗震性能的研究也一直是热点话题。因此,对高墩大跨度加劲钢桁架连续刚构桥在地震作用下的抗震性能研究是有必要的。
目前,国内外学者对桥梁抗震性能研究颇多。在基于 IDA 的倒塌易损性分析方法,国内代表学者有黄盛楠[1]、谷音[2]、吴文朋[3]、陈志伟[4]、周长东[5]等,上述学者分别以不同类型的桥梁为算例进行桥梁抗震性能研究。国外学者 Hwang[6]针对缺乏地震破坏数据地区的桥梁,基于场地特征构造了人工地震动,对该区域典型桥梁进行了地震易损性分析。对现场试验和理论分析之间的差异比较,国外学者 Tavares[7]以加拿大魁北克省三河市的桥梁为例进行了相关研究。
在各损伤状态下,系统的损伤概率均大于构件的损伤概率[8],因此需要探究桥梁构件之间的相关性,对桥梁系统进行易损性计算。本文首先介绍了地震易损性分析流程,然后以某座加劲钢桁架连续刚构桥为例,基于增量动力分析方法,选取了 10 条地震波,对结构进行了非线性时程分析,比较了构件与系统两个层面的横向地震易损性。
1 易损性分析流程
本文以一座加劲钢桁架连续刚构桥为工程背景,借助有限元软件 MIDAS Civil,通过纤维截面划分实现非线性,建立全桥有限元模型。将桥墩作为易损构件,在桥墩墩顶、墩底添加纤维铰,计算在地震荷载的作用下桥墩在该位置的响应,继而得到构件地震易损性曲线,基于一阶界限估计法,计算该桥的系统易损性。
结构发生某种程度破坏的概率,如式(1)所示。

式中:IM为地震动参数;DI为地震需求;C为抗震能力。
本文基于理论易损性分析方法计算结构系统的易损性曲线,其分析流程如图 1 所示。

图1 地震易损性分析流程
2 工程概况与有限元建模
2.1 工程概况
算例桥梁为一座四跨(97+2×180+97)m 加劲钢桁架连续刚构桥,主梁顶板宽 15.0 m,底板宽 11.5 m,顶板、底板和腹板厚度分别为 0.5~1.7 m、0.45~2.5 m 和 0.45~1.5 m。箱内顶、底板处分别设150 cm×50 cm、45 cm×45 cm 梗胁。中支点处横隔墙厚 150 cm,并设有 170 cm×200 cm 进人孔,端支点处横隔墙厚 150 cm,并设有 160 cm×160 cm 进人孔。桥墩编号从左到右依次为 1 #~5 #,其中最高墩为 4 # 墩,墩高 105 m,设置竖杆三角形加劲钢桁,整体式节点,中跨 158 m 范围内设置加劲钢桁,节间长度 12.5 m,主桁中心距 11.5 m,桁高 12.5 m。
2.2 有限元建模
根据桥梁所处场地条件,运用 MIDAS CIVIL 建立全桥非线性有限元模型,如图 2 所示。

图2 算例桥梁有限元模型
2.3 自振特性
自振特性分析是抗震计算的基础,表 1 为该桥前五阶自振特性。

表1 自振特性
该加劲钢桁架连续刚构桥的第一阶振型为 3#、4# 桥墩以及主梁横桥向振动,2# 桥墩没有明显横桥向振动,桥梁与桥墩在竖向以及顺桥向没有明显振动;第二阶振型为 2#、3# 桥墩以及主梁横桥向振动,4# 墩没有明显横桥向振动,桥梁与桥墩在竖向以及顺桥向没有明显振动。其自振特性分析表明,相比于竖桥向和纵桥向,该桥在横桥向的抗震性能较差。因此本文主要分析背景桥梁在横向地震作用下的易损性。
3 损伤指标
在地震易损性分析中,一般将结构损伤状态划分为如表 2 所列的 5 个损伤等级[9]。根据既往研究表明,高墩桥梁由于高阶振型影响,导致墩顶位移与墩底弯矩出现不一致的现象,因此选用曲率延性比作为桥墩的损伤指标。
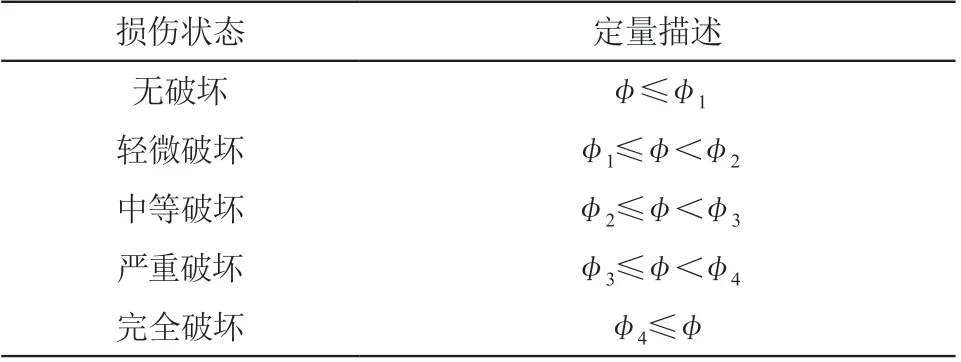
表2 桥墩曲率延性比定义的破坏状态
借助 X-TRACT 软件,对背景桥梁易损构件进行弯矩-曲率分析,其中φ1为首次屈服曲率;φ2为等效屈服曲率;φ3为混凝土压应变达到 0.004 时对应的曲率;φ4为截面极限曲率。
4 地震易损性分析
对选用的 10 条天然地震波进行步长 0.1g的等步长为调幅,调幅区间为 0~1.0g。输入有限元模型并进行非线性分析。
4.1 构件地震易损性
构件易损性分析中,用目标构件需求Sd和其承载能力Sc来计算超越概率,如式(2)所示。

由于Sd和Sc都服从对数正态分布,式(2)可转化为如下所示形式,如式(3)所示。

桥墩需求响应的对数值 ln(μ1)与地震峰值加速度对数值 ln(PGA)的线性回归分析结果如图 3 所示。

图3 不同构件地震需求响应的回归分析
本文中结构反应需求服从对数正态分布,如式(4)所示。

式中:为结构需求平均值;βd为结构需求对数标准差。
依据图 3 所示的线性回归分析结果,得出了如表 3 所列的回归曲线的拟合函数。

表3 不同构件地震响应的概率需求模型
表 3 结果带入公式(3),并进行计算可以得到各桥墩在不同损伤状态下的超越概率。最后以地震动峰值加速度为x轴,构件的损伤超越概率为y轴,绘制如图 4 所示的加劲钢桁架连续刚构桥各桥墩地震易损性曲线。
由图 4 可知,随着 PGA 的的增大,各构件在地震荷载作用下对应各级损伤状态的概率呈增大趋势。在E1(PGA=0.15g)地震作用下 2 # 桥墩、3# 桥墩、4# 桥墩的轻微损伤概率分别是 5.47 %、9.68 %、13.15 %。在E2(PGA=0.32g)地震作用下 3# 桥墩、4# 桥墩发生中等损伤的概率为 65.15 %、67.18 %,均超过 50 %,且其发严重损伤的概率分别为 3.64 %、4.91 %。对于同一构件而言,随着地震动强度的增大,其破坏概率也呈增大趋势,各级易损性曲线呈现先快速增加后逐渐变缓,表明构件进入延性耗能阶段。
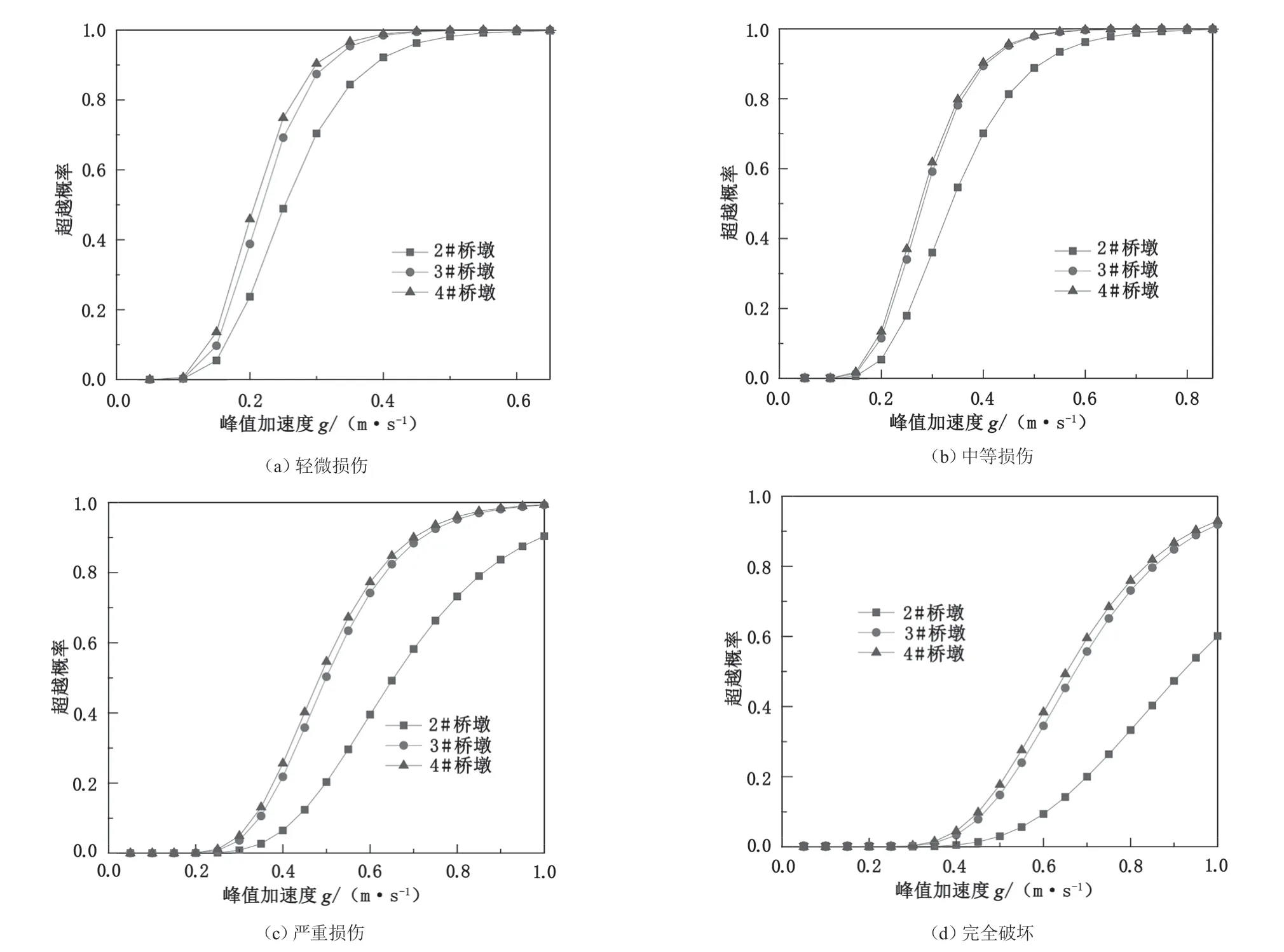
图4 4 种损伤状态构件地震易损性曲线
4.2 系统地震易损性
计算桥梁系统易损性时,需从构件易损性出发,用若干构件的易损性去表征系统易损性。本文采用一阶界限法[10]计算桥梁系统失效概率:

式中:Psys为系统是失效概率;Pfi为第i种构件失效的概率。
采用一阶界限法时,其构件破坏概率的最大值是系统失效概率的下限值,其上限则是则所有构件全部失效的概率。由于未考虑构件之间的相关性,因此给出的上下限区间较宽。绘制得系统易损性曲线,如图 5 所示。
在E1(PGA=0.15g)地震作用下系统的轻微损伤概率的上限为 28.94 %,相较于 2# 桥墩、3# 桥墩、4# 桥墩的 5.47 %、9.68 %、13.15 %,增大幅度为 99.82 %。在E2(PGA=0.32g)地震作用下系统发生严重损伤的概率几乎达到了 30 %,远大于同等条件下 2# 桥墩、3# 桥墩、4# 桥墩的严重损伤概率。其系统易损性同构件易损性变化趋势相同,随着地震动强度的增大,其破坏概率呈增大趋势,易损性曲线也呈现先快速增加后逐渐变缓。通过将图 5 与图 4 进行对比发现,在各损伤状态下,系统的损伤概率相较于构件均会有不同程度的增长,仅从单个构件角度评价桥梁抗震性能是偏安全的。

图5 4 种损伤状态系统地震易损性曲线
5 结论
1)该算例桥梁前四阶振型均为横桥向振动,第一阶振型与第二阶振型有接续迹象,且第三阶、四阶振动振型与第一阶、二阶振型相似。表明振动情况延桥向传播,且在振型叠加下振动幅值有所增加。
2)该算例桥梁在E1(PGA=0.15g)、E2(PGA=0.32g)地震作用下 2# 桥墩、3# 桥墩的轻微损伤概率和中等损伤概率均小于 4# 桥墩,表明在同一地震强度的作用下,构件损伤超越概率与桥墩高度有一定关联。对于该桥各级损伤状态,构件损伤概率与墩高呈正相关,即 4# 墩>3# 墩>2# 墩;各个损伤状态下,地震动峰值加速度与构件的损伤超越概率成正相关。
3)在各损伤状态下,系统的损伤概率相较于构件均会有不同程度的增长;在进行结构的抗震性能评估时,仅从单个构件角度进行分析是偏安全的,还需考虑系统内各构件之间的相关性。Q
