驾驶风格聚类与识别研究

王科银，杨亚会，王思山，杨正才，张建辉

（湖北汽车工业学院，湖北 十堰 442002）

Elander等人［1］在研究交通事故的人为因素时，首次定义驾驶风格是驾驶人多年形成的不同个体选择驾驶的方式，指出驾驶风格包括驾驶速度、超车和行车间距以及违反交通规则的倾向等。驾驶风格对车辆行驶的经济性和安全性有显著影响［2］。驾驶风格的准确聚类和有效识别在驾驶风格研究中扮演重要角色。目前驾驶风格的聚类研究主要是基于问卷调查的主观评价方法和基于驾驶数据的客观评价方法［3］。问卷有多维度驾驶风格量表、驾驶人行为问卷以及驾驶人风格问卷等［4］，都是驾驶人的主观评价，因此更多集中在基于驾驶数据的客观评价方法上。驾驶风格聚类算法主要有层次聚类法［5］、模糊均值聚类法［6］、k邻近算法［7］、k-means聚类算法［8］等。对驾驶风格的识别主要是在驾驶风格聚类的基础上实现对特定驾驶特性的有效判别，用到的算法主要有基于规则的算法［9］、模糊逻辑算法［10］、ANN算法［11］、SVM算法［12］等。上述研究在特定的驾驶风格表征指标下实现了对驾驶风格的聚类或识别，但缺乏对驾驶风格表征指标的贡献度分析以及数据降维对不同识别算法识别精度影响的相关研究。基于此，文中选取NGSIM实测驾驶数据，提取包含换道特征在内的车辆16s完整行驶轨迹，运用因子分析法对初选的21个特征参数进行降维，选用k-mean聚类算法对所得样本进行聚类分析，深入研究了自然驾驶状态下驾驶风格的表征要素；在此基础上分别搭建支持向量机（support vector machine,SVM）和人工神经网络（artificial neural network,ANN）驾驶风格辨识模型，并对比数据降维前后的识别准确率。

1 NGSIM数据筛选和预处理

1.1 原始数据与滤波处理

选取美国联邦公路管理局NGSIM项目［13］提供的Ⅰ-80路段行车数据。该项目采用摄像机视频拍摄方式逐帧（0.1 s/帧）获取拍摄区域所有车辆的行车轨迹和车辆特征数据，每个数据样本包括车辆编号、数据帧号、数据总帧、标准时间、采集区域坐标系的X坐标值、采集区域坐标系的Y坐标值、标准地理坐标系的X指标值、标准地理坐标系的Y坐标值、车辆长度、车辆宽度、车辆类型、车辆速度、车辆加速度、车道编号、跟驰前车编号、跟驰后车编号、车头间距和车头时距等18个参数。样本拍摄的时间为2005年6月15日16：00-16：15、17：00-17：15和17：15-17：30时间段，共计45min。Ⅰ-80检测路段如图1所示，检测路段长度共计503m，其中编号1～5为行车道，编号6为集散车道，编号7为入口匝道，编号8为出口匝道。

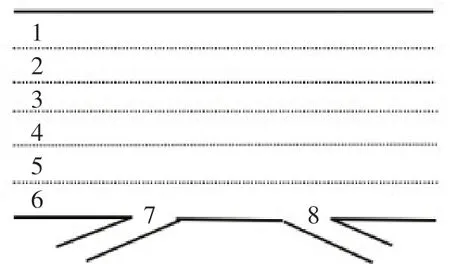
图1 Ⅰ-80路段示意图

原始数据由视频处理而得，存在异常值和测量误差。为了获得较为精确的车辆行驶数据，采用Savitzky-Golay滤波算法对数据进行平滑处理。Savitzky-Golay滤波是移动窗口加权平均算法，原理是对一定长度窗口内的数据点进行多项式的最小二乘拟合［14］。选取窗口长度为21、多项式阶数为3，对原始数据进行平滑处理。编号为3261的车在一段时间内的横向位置、车速、加速度的平滑效果如图2所示。

图2 Savitzky-Golay滤波器平滑效果图

1.2 数据筛选

按照6条规则对Ⅰ-80平滑后的数据进行筛选，得到817辆车完整换道特征的行驶数据规则如下：1）车辆类型选择为小轿车。NGSIM数据集中车辆类型包含摩托车、小轿车和大型车，但摩托车和大型车的数据相对较少。为了获得同一类型车辆一定数量的行驶数据，选择数据相对较多的小轿车作为研究对象。2）提取只有1次换道行为的车辆行驶数据。当车辆存在多次换道时，有可能是要驶离高速急于换道至匝道或者刚驶入高速急于换道至快车道或是其他情况下的非正常行驶状态。3）剔除没有前车的车辆数据。驾驶风格聚类分析时需要跟车距离和车头时距的相关参数，没有前车会导致参数缺失，对聚类结果的准确性产生影响；当没有前车时，车辆处于过度自由行驶状态，无法体现由于驾驶环境因素导致的正常换道行为。4）剔除由7号车道换至6号车道或者由6号车道换至8号车道的车辆数据。由7号车道换至6号车道的车辆为从入口匝道驶入高速的车辆，由6号车道换至8号车道的车辆为由高速驶入出口匝道的车辆，2类车辆都为强制换道车辆，不属于文中研究内容。5）选取具有16s完整换道轨迹的车辆数据。因为文中预深入研究可以表征驾驶人驾驶风格的特征参数，所选数据除了包含纵向跟驰特征还应包含完整的横向换道特征。根据文献［15-16］，几乎所有的正常换道车辆在16s都能完成单次换道，故选择16s作为实验数据的时间长度，即车辆换道前后各8s。6）剔除出现中途停车的车辆。数据集中存在车速为0km·h-1的情况，该部分车辆因某些原因出现中途停车或是测量误差所致，需要剔除。

2 驾驶风格表征

2.1 表征指标提取

对于驾驶风格评价指标的选取没有统一的标准，不同学者选取的评价指标不尽相同，选取的评价指标越多越能够全方位表征驾驶人的驾驶风格。文中选取21个评价指标，如表1所示，以期全方位表征驾驶人的驾驶风格并从中寻找能够更好表征驾驶人驾驶风格的评价指标。车辆行驶速度、加速度、跟车距离和车头时距由数据集直接获得。其他指标的计算如下：

表1 驾驶风格表征指标

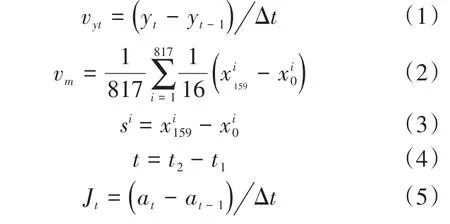
2.2 因子分析法降维

初步选取的21个评价指标能较全面地反映驾驶人在包含换道过程16s行车轨迹中表现出来的驾驶习性，但是各指标的重要程度不同，且指标之间存在信息冗余［17］。为减少21个评价指标之间的相关性，减少信息重叠，采用因子分析法对数据进行降维［18］。因子分析之前，为验证数据的可行性，首先对样本数据进行KMO（Kaiser-Meyer-Olkin）检验和Bartlett’s球状检验。KMO检验统计量和Bartlett’s球状检验统计量都是用来表示特征之间相关性的指标，KMO取0～1，值越大意味着变量间的相关性越强，原变量越适合因子分析，一般认为KMO检验统计量在0.7 以上、Bartlett’s球状检验统计量伴随概率小于0.01 适合作因子分析。21个指标KMO检验概率为0.7052、Bartlett’s球状检验伴随概率为0，说明可进行因子分析。

利用Python的factor_analyser库对数据做因子分析。选取主成分个数为4，提取方法为主成分分析法，旋转方法为最大方差法，得到特征值、方差贡献率、累计方差贡献率如表2所示。由表2可知，4个特征根反映出来的信息量占全部信息的70.76%，高于70%，满足要求，因此选取这4个特征根进行分析。对因子进行旋转，得到因子载荷矩阵如表3所示，可看出：1）主成分1与X1～X2、X10～X11相关系数较大，主要体现车辆的纵向运动特征，命名为“纵向因子”；2）主成分2与X7～X9、X19～X21相关系数较大，主要体现车辆的加速度特征，命名为“加速因子”；3）主成分3与X4～X6间相关系数较大，主要体现车辆的横向行驶特征，命名为“横向因子”；4）主成分4与X13～X14、X16～X17相关系数较大，主要体现车辆的跟车特征，命名为“跟驰因子”。由因子得分系数矩阵（表4）得到公共因子的表达式：

表2 因子分析相关数据

表3 旋转后的因子载荷矩阵

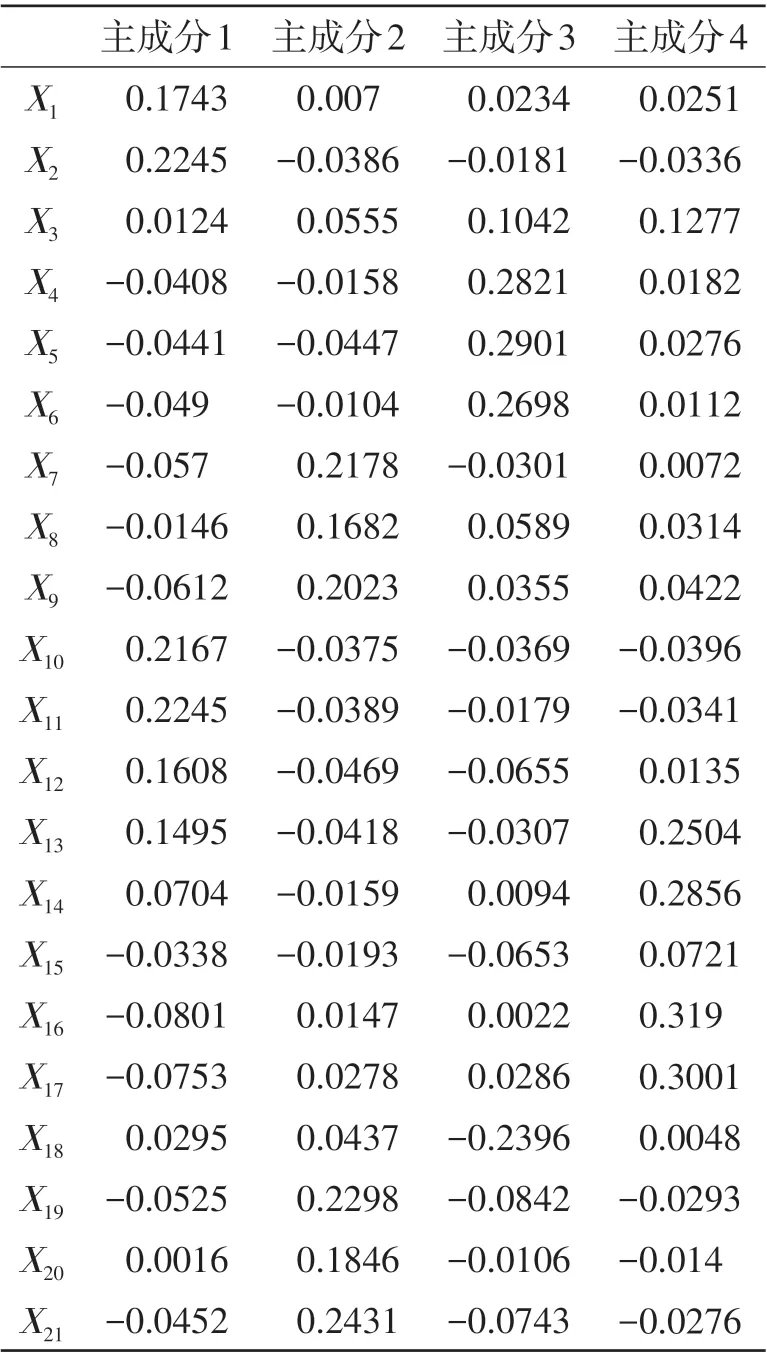
表4 因子得分系数矩阵

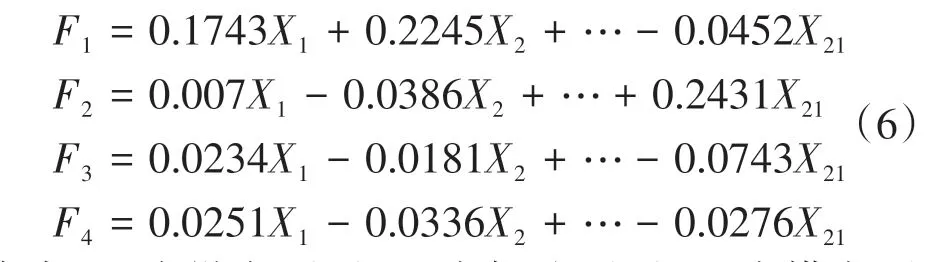
式中：F1为纵向因子；F2为加速因子；F3为横向因子；F4为跟驰因子。

3 驾驶风格k-means聚类

3.1 k-means算法

聚类是对观测数据进行划分，使得同簇内的数据彼此相似，不同簇之间不相似，是无监督学习方法［19］。聚类算法中的k-means聚类因易于实现、聚类效果好而被广泛应用。k-means算法的基本思想是按照样本数据之间的距离大小，将样本划分为k个簇，目标是最小化平方误差E：

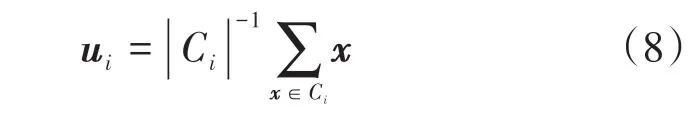
式中：Ci为簇；ui为簇Ci的均值向量。

k-means算法的流程如下：1）从样本集M中选择k个数据点作为初始聚类中心；2）分别计算每个样本点到聚类中心的距离di：

找到距离该点最近的聚类中心，将该样本归为对应的簇；3）将所有点归属到簇之后，重新计算每个簇的中心，获得新的聚类中心；4）反复迭代步骤2）～3），直至终止条件。

3.2 聚类结果

运用k-means算法对4个因子进行聚类分析。定义聚类中心个数k为3，得到聚类中心因子值和各类别数目如表5所示。对比聚类中心差别最大的F1可看出，类型0的驾驶人纵向因子最小，倾向于选择较低的速度驾驶，驾驶风格较谨慎；类型2的驾驶人纵向因子最大，倾向于选择较大的速度驾驶，驾驶风格较激进。对比F2，类型0的驾驶人加速因子绝对值最小，说明其驾驶风格在加速度的表现上最为谨慎；类型2的驾驶人加速因子绝对值最大，说明其驾驶风格在加速度的表现上最为激进；这和驾驶人的驾驶风格表现在车辆纵向行驶是一致的。对比F3可看出驾驶人的驾驶风格在车辆横向运动方面的表现和在F1、F2上的表现一致。F4没能表现上述规律，对驾驶风格聚类的贡献度相对较低。F1～F3对驾驶风格的贡献度较高。结合样本属性可得，实验数据中谨慎型驾驶数据276组，一般型驾驶数据355组，激进型驾驶数据186组。

表5 因子得分系数矩阵聚类中心因子和类别数

4 驾驶风格识别模型

对驾驶风格聚类分析，得到每个样本所属类别，建立2类机器学习分类模型，即SVM模型和ANN模型，对比2类分类模型在驾驶风格识别中的优劣，为驾驶风格识别模型的选择提供参考。

4.1 SVM模型

SVM具有完美的数学形式、直观的几何解释和良好的泛化能力［20］，用来解决二分类问题，输入样本集为（x1,y1）,（x2,y2）,…,（xm,ym），其中xi为n维特征向量，y为二元输出，值为1或者-1；输出为分离超平面的参数ω*和b*和分类决策函数。算法过程如下：选择合适的核函数

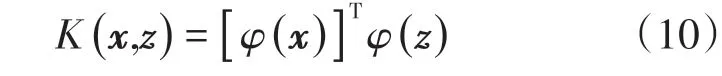
和惩罚系数C（C＞0），构造约束优化问题：

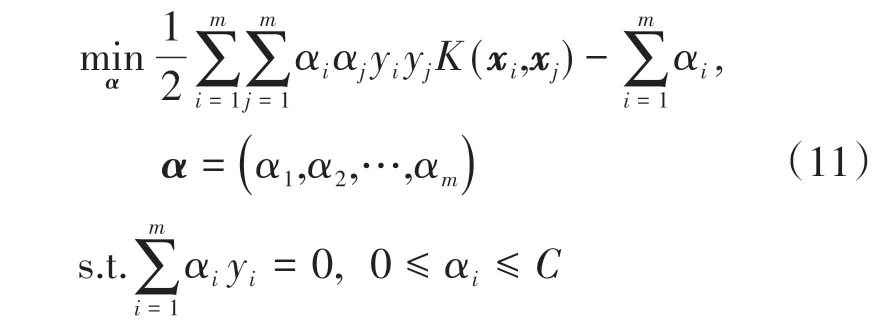
式中：α为拉格朗日因子向量；用SMO算法求解上述优化问题，得到αi*；根据式（12）求得ω*：

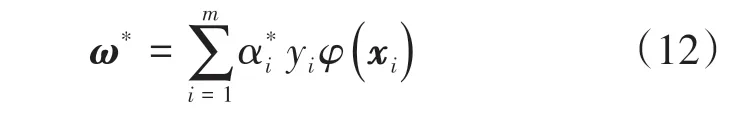
找出所有的S个支持向量，即满足0＜αs对应的样本（xs,ys），根据式（13）计算出b*：

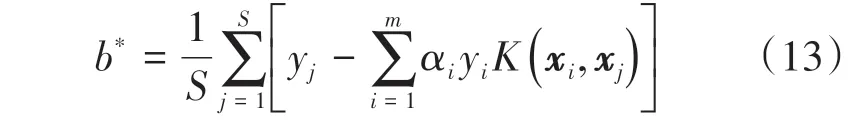
最终得到支持向量机模型：

将SVM用于解决多分类问题时，要将其进行改进。标准的改进算法是构造多个SVM分类器，第i个分类器用第i类中的训练样本作为正样本，其他样本作为负训练样本。

4.2 ANN模型

ANN模型［21］具有高计算能力、泛化能力和非线性映射等特点，深度学习的迅猛发展使ANN广泛应用于人工智能的各个领域。ANN基本结构如图3所示。输入向量为X=（x1,x2,…,xn），隐含层有q个神经元，输入层到隐含层的连接权重为V，输出向量为Y=（y1,y2,…,ym），隐含层到输出层的连接权重为W，则隐含层输出Z为

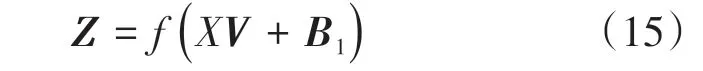
图3 ANN基本结构

最终输出Y为

式中：f为激活函数；B1和B2为偏置向量。ANN的训练过程就是反复迭代，确定V、W、B1和B2。

4.3 结果分析

随机选取817组样本数据中的550组作为训练样本，其余数据作为测试样本，分别构建SVM模型和ANN模型，运用降维前后的数据进行训练和测试。SVM的核函数选择为3次多项式，惩罚系数为1；ANN模型隐含层设置为3层，神经元个数分别为10、20、10，传递函数为sigmoid函数，随机初始化权重和偏置，使用自适应学习率优化算法，迭代步数设置为5000。测试结果见表6：SVM模型和ANN模型在数据降维前后的识别率都大于90%，说明都可实现对驾驶风格的准确辨识；SVM模型的识别精度高于ANN模型，说明SVM方法在小样本上的有效性；降维后的数据识别率高于降维前，因为在对驾驶风格分类时用的是降维后的数据。

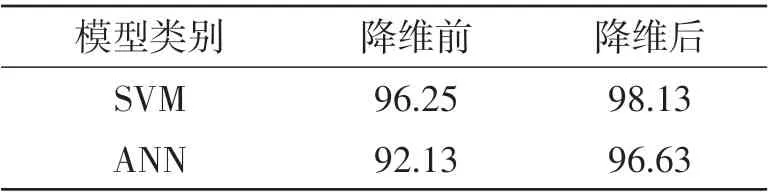
表6 模型识别准确率 %

5 结语

为深入探索驾驶风格表征指标，实现驾驶风格准确聚类和有效识别，基于NGSIM实测数据，采用一定的规则对原始数据平滑、筛选，获得了包含完整换道特征的车辆行驶数据。选取21个指标表征驾驶风格，采用因子分析法实现数据降维。基于k-means算法对降维后的数据进行驾驶风格聚类，聚为谨慎型、一般型和激进型，通过聚类分析发现车辆行驶速度、加速度和横向速度的行驶特征更能表征驾驶风格。在此基础上，搭建了SVM和ANN驾驶风格识别模型并完成模型训练，对比数据降维前后的识别准确率，发现2类模型都可实现驾驶风格的准确识别，SVM模型的识别精度更高。