石英晶体板型表面波陀螺仪研究*
2021-10-15吴荣兴王晓明
吴荣兴,王晓明,郑 东
(1.宁波职业技术学院 建筑工程学院,浙江 宁波 315800; 2.宁波大学 机械与力学学院,浙江 宁波 315211)
0 引 言
各类声表面波气体、质量和偏场传感器已被广泛应用于各种复杂环境下的检测工作[1~3]。主要工作原理是通过声学和电学参数的测量来推定所处环境因素或物质特性[3~7]。过去认为声表面波在液体检测中由于存在严重能量衰减,无法检测其有效信号,目前证明可以将声表面波技术应用于微流体的特性检测[8]。在惯性传感器领域,理论研究表明哥氏力对声表面波的传播有抑制作用,并且存在着对应关系,可以用来检测旋转场的旋转频率[9,10]。大部分声表面波陀螺效应传感器所建的模型都是基于半无限大各向同性弹性体结构,而真实的压电声波器件往往采用各向异性的压电材料组成的层状板型结构[11,12]。虽然实验研究结果显示陀螺效应对声表面波传播有着显著影响,但是实验样机的分辨率和精度都无法满足传感器要求[13]。因此,完整建立更为真实的压电声波陀螺效应传感器模型和精确分析成为一项迫切的工作。
这里分析了声表面波在考虑旋转场作用下的半无限石英晶体和无限大石英晶体板内的传播特性,获得了波速、板厚、旋转轴角度和旋转频率之间的对应关系,为实际声表面波陀螺效应传感器的研制提供了理论指导。
1 半无限大石英晶体的声表面波
声表面波在考虑旋转场作用下的石英晶体板内传播如图1所示。旋转场的旋转频率为Ω,旋转轴与x1轴的夹角为θ。首先考虑底部是半无限大石英晶体的情况。

图1 带旋转场的石英晶体板
当声表面波在半无限大石英晶体内沿着x1方向传播时[14,15],位移和电势可以假设为
u1=A1ekβx2eik(x1-ct),u2=A2ekβx2eik(x1-ct),
u3=A3ekβx2eik(x1-ct),φ=A4ekβx2eik(x1-ct)
(1)
式中u1(u2,u3),φ,A1(A2,A3,A4),k,β,x1(x2),c和t分别为声表面波的位移、电势、振幅、波数、衰减系数、坐标、波速和时间变量。
基于式(1)的位移假设,获得应变和电场分量为
S1=iku1,S2=kβu2,S3=0,
S4=kβu3,S5=iku3,S6=kβu1+iku2,
E1=-ikφ,E2=-kβφ,E3=0
(2)
式中Sp(p=1,2,…,6)和E1(E2,E3)为各方向的应变和电场分量。
基于应变和电场分量式(2),可以得到应力和电位移分量为
Tp=k[(cp 6β+icp1)u1+(cp 2β+icp 6)u2+
(cp 4β+icp 5)u3+(e2pβ+ie1p)φ],
Dj=k[(ej 6β+iej 1)u1+(ej 2β+iej 6)u2+
(ej 4β+iej 5)u3+(εj 2β+iεj 1)φ],
p=1,2,3,4,5,6,j=1,2,3
(3)
式中Tp,Dj,cpq(q=1,2,…,6),ejp和εij(1,2,3)分别为各方向应力、电位移、石英晶体材料的弹性常数、压电常数和介电常数[8]。
考虑旋转场作用下半无限大石英晶体的运动方程为[12]
(4)
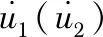
将应力和电位移表达式(3)代入运动方程式(4),经整理后得到关于A1(A2,A3,A4)的方程组。如这些振幅存在非零解,必须要求振幅A1(A2,A3,A4)的系数行列式的值为零。这样可以获得关于衰减系数β的4对解,取其沿着深度方向呈衰减的衰减系数[14,15],重写位移和电势如下
(5)
式中A4n(n=1,2,3,4)和βn为新定义的振幅和获得的衰减系数。
根据新位移和电势式(5),基于式(3),重写应力和电位移表达式。当声表面波在如图1所示的半无限大石英晶体内沿着x1方向传播时,必须满足力学边界条件[14,15]。同时对于石英晶体这一压电弹性体,除了满足力学边界条件外,还应该满足电学边界条件[14,15]。全部边界条件如下
T2=T4=T6=D2=0,x2=0
(6)
将新的应力和电位移表达式代入边界条件表达式(6),可以得到振幅A4n的四个方程组。若声表面波存在非零解,必然要求其系数行列式的值为零,这样就建立了声表面波的波速方程。可以分别绘制出绕x1轴和x2轴的旋转频率和声表面波波速的关系曲线如图2所示。这里选用的石英晶体切型为传感器领域常用的ST切型,其材料参数见文献[8]。
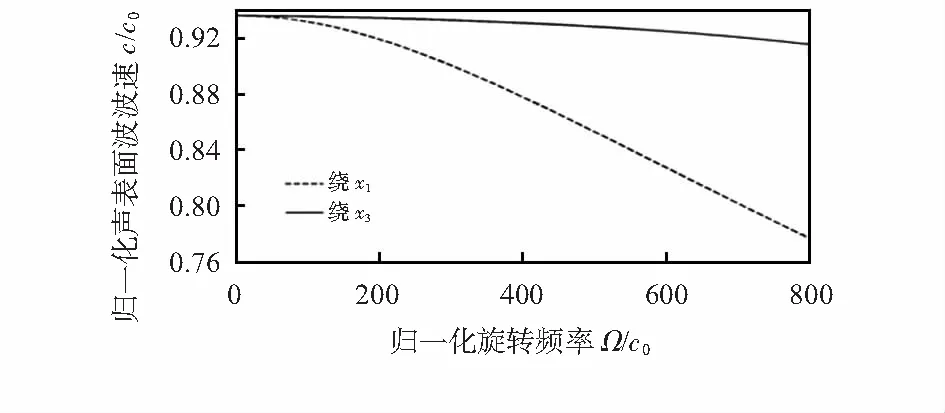
图2 半无限大石英晶体的波速—旋转频率曲线
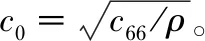
在实际工作环境中,并不能确定旋转场的旋转轴与声表面波传播方向的角度。可以进一步绘制在一定旋转频率下,即Ω/c0=500时,声表面波波速和旋转轴角度之间的关系如图3所示。
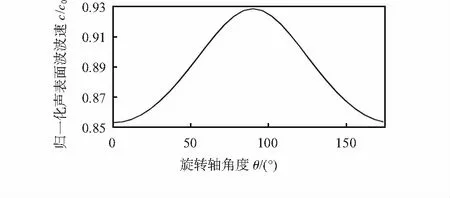
图3 半无限大石英晶体的波速—旋转轴角度的关系曲线
从图3可以发现,随着旋转轴角度的变化,声表面波波速也发生变化。在实际应用中,不仅需要检测出旋转场的旋转频率,也需要检测出旋转轴角度。结合图2和图3,可以进行联立求解,确定旋转场的旋转频率和旋转轴角度[14,15]。
本研究初步纳入了2015年1月至2017年1月期间就诊于上海市浦东医院眼科的患者82例(100眼),于2015年1月获得上海市浦东医院伦理委员会批准(批号:LW2015-001),遵循赫尔辛基宣言。所有患者均告知检查目的及检查内容,手术前均签署手术知情同意书。
2 无限大石英晶体板的声表面波
当声表面波在图1所示的无限大石英晶体板内传播时,其位移将会呈现出板波的形式[16]。因此,运动方程式(4)获得的衰减系数将全部应用到新的位移和电势假设。按照式(5)和式(3)可以写出新的位移、电势、应力和电位移表达式。
对于如图1所示的半无限大石英晶体板的上下表面,其应力和电位移边界条件如下
T2=T4=T6=D2=0,x2=0,
T2=T4=T6=D2=0,x2=-h
(7)
式中h为石英晶体板的板厚。为了计算简单,对石英晶体板厚度进行如下归一化处理
H=h/ξ,kξ=2π,kh=2πH
(8)
式中H和ξ分别为石英晶体板的归一化厚度和声表面波波长,这里无限大板的材料仍然取ST切石英晶体作为研究对象。
从图4~图5可以发现,声表面波在无限大石英晶体板内传播时,出现了两个声表面波波速,并且随着石英晶体板厚度的增加,波速的上下分支逐渐接近。这一计算结果符合过去的研究和实验结果[14,15]。同样随着旋转频率的增加,石英晶体板内各声表面波波速都在减小。与半无限大石英晶体的结果类似,绕轴旋转时的波速减小趋势更快,并且相应的线性关系可以应用于旋转场的传感[10~12]。这里建立的模型更加符合实际传感器的层状板型结构。
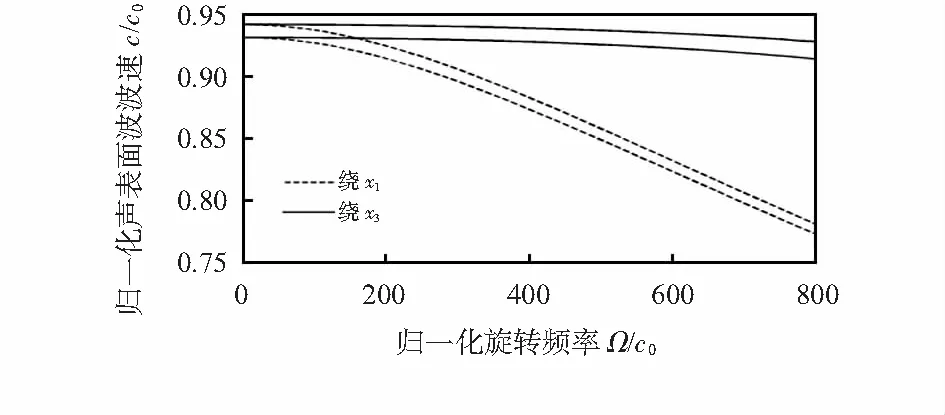
图4 半无限大石英晶体板的波速—旋转频率曲线(三个波长)
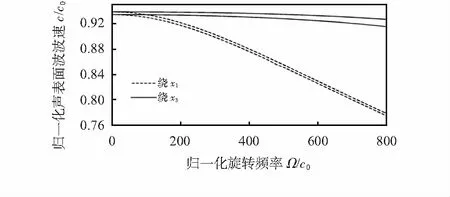
图5 半无限大石英晶体板的波速—旋转频率曲线(四个波长)
3 结 论
通过对考虑陀螺效应的声表面波传播方程的求解,获得了声表面波波速、旋转频率和旋转轴角度之间的关系曲线图。研究结果表明:旋转场对于声表面波的传播都有着显著影响,特别是绕声表面波传播方向旋转时影响效果更为明显。当声表面波在无限大石英晶体板传播时,随着板厚的增加,声表面波波速逐渐趋向于无限大的情况。这里所建的模型为考虑压电效应的层状结构,更符合实际的声表面波压电器件分析模型。
